Optical Solitons with Tilted Wavefronts

The propagation of nonresonant solitons with phase and group wavefronts tilted with respect to each other is studied. It is shown that the tilt of fronts leads to the redefinition of the group velocity dispersion, introducing an additional anomalous contribution to it. As a result, light temporal and spatiotemporal solitons can be formed at the normal dispersion of the group velocity and focusing nonlinearity, including the cases of absence of this dispersion. A spatiotemporal soliton is a structure that is extended along group fronts normally to the plane of polarization and is localized in all directions perpendicular to the direction of extension of the soliton.

1 INTRODUCTION

Optical solitons can be spatial and temporal. Spatial solitons are continuous light energy beams that are infinitely extended in the direction of propagation and are limited in the transverse directions. They are formed as a result of mutual compensation of the nonlinear transverse self-focusing and diffraction divergence. Temporal solitons are short pulses that are localized in the direction of propagation and are infinitely extended in the transverse directions. They are due to the mutual compensation of nonlinear self-compression and dispersion spreading. It is important that a temporal soliton in the presence of focusing nonlinearity is formed if the group velocity dispersion (GVD) is anomalous. If nonlinearity is defocusing, GVD should be normal. Thus, focusing nonlinearity and diffraction are involved in the formation of spatial solitons, and nonlinearity and dispersion are responsible for the formation of temporal solitons.

A spatiotemporal soliton (or light bullet) is a stable energy bunch localized in all directions propagating in space. Considering the light bullet as a combination of the spatial and temporal solitons, one can conclude that its formation requires the presence of focusing nonlinearity, anomalous GVD, and diffraction in a homogeneous medium.

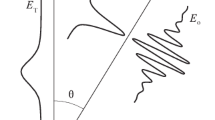
Laser pulses with tilted wavefronts are currently used in laboratories for various aims [1–8]. The phase and group wavefronts of these pulses are noncollinear with respect to each other and tilted to each other by an angle θ. The angle between the phase, ${{v}_{{{\text{ph}}}}}$, and group, ${{v}_{{\text{g}}}}$, velocities of the pulse is obviously the same.

The effect of diffraction is reduced to the bending of phase wavefronts. This in turn results in the transverse broadening of the pulse. Because of the tilt of phase wavefronts, the projection of diffraction broadening on the direction of the group velocity of the pulse leads to its spreading in the direction of propagation. This spreading is similar to the effect of dispersion. Thus, varying the angle between phase and group wavefronts, one can control the effective dispersion, including its sign, owing to diffraction. Can in this case diffraction replace dispersion and, thereby, serve as one of the mechanisms of formation of temporal and spatiotemporal solitons? The aim of this work is to answer this question.

2 EQUATION FOR THE ENVELOPE OF A NONRESONANT PULSE

Let phase wavefronts of the pulse with the carrier frequency ω incident on the isotropic nonresonant medium propagate along the z' axis. The group velocity is directed along the z axis that lies in the (z', x') plane in the Cartesian coordinate system and makes the angle θ with the z' axis (Fig. 1). Let the plane of polarization of the pulse be parallel to the y axis. Correspondingly, the electric field E of the pulse can be represented in the form

$$E = \psi {{e}^{{i(\omega t - kz')}}} + \psi {\text{*}}{{e}^{{ - i(\omega t - kz)}}},$$

(1)

where $\psi (z,x,y,t)$ is the slowly varying envelope of the pulse field and k is the wavenumber.

Fig. 1.

Schematic of the spatiotemporal soliton with (dashed lines) the phase and group wavefronts tilted to each other by the angle θ.

Since imaginary exponentials of the z' coordinate in Eq. (1) are rapidly oscillating, we separate the second derivative with respect to this coordinate in the wave equation

$$\frac{{{{\partial }^{2}}E}}{{\partial z{\kern 1pt} {{'}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} = \frac{{4\pi }}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}P}}{{\partial {{t}^{2}}}} - \Delta _{ \bot }^{'}E.$$

(2)

Here, c is the speed of light in vacuum, $\Delta _{ \bot }^{'} = {{\partial }^{2}}{\text{/}}\partial x{\kern 1pt} {{'}^{2}}\; + {{\partial }^{2}}{\text{/}}\partial y{\kern 1pt} {{'}^{2}}$ is the Laplacian transverse with respect to the z' axis, and P is the polarization response of the medium induced by the electric field of the pulse.

Further, we conventionally represent the polarization response P as the sum of its linear and nonlinear parts, take into account perturbatively the time dispersion of its linear part, and neglect the dispersion of the nonlinear part. As a result, substituting Eq. (1) into Eq. (2) and neglecting derivatives of $\psi$ higher than the second derivative, we obtain (see, e.g., [9])

$$\begin{gathered} i\left( {\frac{{\partial \psi }}{{\partial z{\kern 1pt} '}} + \frac{1}{{{{v}_{{\text{g}}}}}}\frac{{\partial \psi }}{{\partial t}}} \right) = \frac{c}{{2n\omega }}\left( {\frac{{{{\partial }^{2}}\psi }}{{\partial z{\kern 1pt} {{'}^{2}}}} - \frac{1}{{v_{{\text{g}}}^{2}}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}}} \right) \\ - \;\frac{\beta }{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} + F({\text{|}}\psi {{{\text{|}}}^{2}})\psi + \frac{c}{{2n\omega }}\Delta _{ \bot }^{'}\psi . \\ \end{gathered} $$

(3)

Here, n is the refractive index at the frequency ω, $\beta = \partial (1{\text{/}}{{v}_{{\text{g}}}}){\text{/}}\partial \omega$ is the second-order GVD coefficient, and $F({\text{|}}\psi {{{\text{|}}}^{2}})$ is the function describing optical nonlinearity.

We pass to the system of z and x coordinates rotated with respect to the system of z' and x' coordinates by the angle θ using the formulas of transformation $z = z{\kern 1pt} '\cos \theta + x{\kern 1pt} '\sin \theta$ and $x = - z{\kern 1pt} '\sin \theta + x{\kern 1pt} '\cos \theta$. Then, Eq. (3) takes the form

$$\begin{gathered} i\left( {\cos \theta \frac{{\partial \psi }}{{\partial z}} + \frac{1}{{{{v}_{{\text{g}}}}}}\frac{{\partial \psi }}{{\partial t}}} \right) = i\sin \theta \frac{{\partial \psi }}{{\partial x}} + \frac{c}{{2n\omega }} \\ \times \;\left( {\frac{{{{\partial }^{2}}\psi }}{{\partial {{z}^{2}}}} - \frac{1}{{v_{{\text{g}}}^{2}}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} + {{\Delta }_{ \bot }}\psi } \right) - \frac{\beta }{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} + F({\text{|}}\psi {{{\text{|}}}^{2}})\psi , \\ \end{gathered} $$

(4)

where ${{\Delta }_{ \bot }} = {{\partial }^{2}}{\text{/}}\partial {{x}^{2}} + {{\partial }^{2}}{\text{/}}\partial {{y}^{2}}$ is the Laplacian transverse to the z axis.

The right-hand side of Eq. (4) contains relatively small terms including derivatives with respect to coordinates perpendicular to the group velocity, as well as terms small in the parameter (ωτ_p)^–1, where τ_p is the time duration of the pulse. Under these conditions, it is possible to use the unidirectional propagation approximation along the z axis [10], which, in par-ticular, corresponds to the inclusion of the transverse dynamics of the pulse in the paraxial approximation. According to the left-hand side of Eq. (4), the velocity of this propagation is ${{v}_{{\text{g}}}}\cos \theta$. Consequently, $\frac{{\partial \psi }}{{\partial z}} \approx - \frac{1}{{{{v}_{{\text{g}}}}\cos \theta }}\frac{{\partial \psi }}{{\partial t}}$ can be set on the right-hand side of Eq. (4). As a result, we arrive at the equation

$$\begin{gathered} i\left( {\cos \theta \frac{{\partial \psi }}{{\partial z}} - \sin \theta \frac{{\partial \psi }}{{\partial x}}} \right) \\ = - \frac{{{{\beta }_{{{\text{eff}}}}}}}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} + F({\text{|}}\psi {{{\text{|}}}^{2}})\psi + \frac{c}{{2n\omega }}{{\Delta }_{ \bot }}\psi , \\ \end{gathered} $$

(5)

where $\tau = t - z{\text{/}}v$,

$$v = {{v}_{{\text{g}}}}\cos \theta ,$$

(6)

$${{\beta }_{{{\text{eff}}}}} = \beta - \frac{c}{{n\omega v_{{\text{g}}}^{2}}}\mathop {\tan }\nolimits^2 \theta .$$

(7)

The second term in Eq. (7) appearing because of diffraction makes a contribution to the second-order GVD. Since this contribution is negative, the diffraction of the pulse with tilted wavefronts promotes the formation of anomalous GVD. Below, the second term in Eq. (7) will be called diffraction GVD. A similar situation was considered in [1, 11] in application to the optical method of terahertz radiation generation.

3 TEMPORAL SOLITON

In the presence of Kerr nonlinearity when $F({\text{|}}\psi {{{\text{|}}}^{2}}) = \alpha {\text{|}}\psi {{{\text{|}}}^{2}}$, where $\alpha = 6\pi \omega {{\chi }^{{(3)}}}{\text{/}}cn$ and ${{\chi }^{{(3)}}}$ is the third-order nonlinear optical susceptibility, Eq. (5) takes the form

$$\begin{gathered} i\left( {\cos \theta \frac{{\partial \psi }}{{\partial z}} - \sin \theta \frac{{\partial \psi }}{{\partial x}}} \right) \\ = - \frac{{{{\beta }_{{{\text{eff}}}}}}}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} + \alpha {\text{|}}\psi {{{\text{|}}}^{2}}\psi + \frac{c}{{2n\omega }}{{\Delta }_{ \bot }}\psi . \\ \end{gathered} $$

(8)

Setting $\partial \psi {\text{/}}\partial x = {{\Delta }_{ \bot }}\psi$ = 0, we obtain the solution of Eq. (8) in the form of the one-dimensional (temporal) soliton

$$\psi = {{\psi }_{{\text{m}}}}{{e}^{{i\frac{{{{\beta }_{{{\text{eff}}}}}z}}{{2\tau _{{\text{p}}}^{2}\cos \theta }}}}}{\text{sech}}\left( {\frac{{t - z{\text{/}}v}}{{{{\tau }_{{\text{p}}}}}}} \right),$$

(9)

where

$${{\psi }_{{\text{m}}}} = \frac{1}{{{{\tau }_{{\text{p}}}}}}\sqrt { - \frac{{{{\beta }_{{{\text{eff}}}}}}}{\alpha }} $$

(10)

and the velocity of propagation is given by Eq. (6).

It is seen that the light temporal soliton (9) exists if β_eff/α < 0. The Kerr nonlinearity in most of the solid dielectrics is focusing $(\alpha \sim {{\chi }^{{(3)}}} > 0)$. Consequently, β_eff < 0 should be the case. In particular, let β = 0. For example, this equality for fused silica is satisfied at ω ≈ 1.0 × 10¹⁵ s^–1 [12]. Then, using Eqs. (7) and (10) and the expression for α, we write

$${{\psi }_{{\text{m}}}} = \frac{{c\tan \theta }}{{{{v}_{{\text{g}}}}\omega {{\tau }_{{\text{p}}}}\sqrt {6\pi {{\chi }^{{(3)}}}} }}.$$

(11)

The maximum intensity $I = c\psi _{{\text{m}}}^{{\text{2}}}{\text{/}}2\pi$ of the soliton is given by the expression

$$I = \frac{1}{{n{{n}_{2}}}}{{\left( {\frac{{c\tan \theta }}{{n{{v}_{{\text{g}}}}\omega {{\tau }_{{\text{p}}}}}}} \right)}^{2}}.$$

(12)

Here, ${{n}_{2}}$ is the nonlinear refractive index determining the additive ${{n}_{2}}I$ to the linear index n; it is related to χ⁽³⁾ as cn²n₂ = 12π²χ⁽³⁾ [13].

For fused silica nn₂ ≈ 5 × 10^–16 cm²/W [13], at the duration τ_p ~ 10^–12 s, and at the tilt angle θ = 45°, the intensity is I ~ 10⁹–10¹⁰ W/cm².

Thus, the diffraction GVD in real experiments can promote the formation of the temporal soliton with tilted wavefronts.

4 SPATIOTEMPORAL SOLITON

Since the diffraction GVD is anomalous, it should stimulate the formation of the spatiotemporal soliton [14–20]. Following the standard approach [14, 18], we represent the envelope ψ in the form

$$\psi = \sqrt \rho {{e}^{{iqx - n\omega \varphi /c}}},$$

(13)

where ρ and φ are the unknown functions of the variables z and y and

$$\xi = \sqrt {\frac{c}{{n\omega {\text{|}}{{\beta }_{{{\text{eff}}}}}{\text{|}}}}} \tau .$$

(14)

The effective GVD is considered anomalous (β_eff < 0).

The quantity ρ is obviously proportional to the local intensity of the pulse.

Substituting Eq. (13) into Eq. (5), taking into account Eq. (14), and separating the real and imaginary parts, we arrive at the system of equations

$$\frac{{\partial \rho }}{{\partial \zeta }} + {{\nabla }_{2}}(\rho {{\nabla }_{2}}\varphi ) = 0,$$

(15)

$$\begin{gathered} \frac{{\partial \varphi }}{{\partial \zeta }} + \frac{{{{{({{\nabla }_{2}}\varphi )}}^{2}}}}{2} - \frac{c}{{n\omega }}F(\rho ) + \frac{1}{2}{{\left( {\frac{c}{{n\omega }}} \right)}^{2}}\left( {{{q}^{2}} + \frac{{2n\omega }}{c}q\sin \theta } \right) \\ = \frac{1}{2}{{\left( {\frac{c}{{n\omega }}} \right)}^{2}}\frac{{{{\Delta }_{2}}\sqrt \rho }}{{\sqrt \rho }}. \\ \end{gathered} $$

(16)

Here, $\zeta = z{\text{/}}\cos \theta$, ${{\nabla }_{2}}$ is the nabla operator in the variables y and ξ, and ${{\Delta }_{2}}$ is the Laplacian in these variables.

Let the optical nonlinearity function have the form

$$F{{({\text{|}}\psi {\text{|}})}^{2}}) = \alpha {\text{|}}\psi {{{\text{|}}}^{2}} - \sigma {\text{|}}\psi {{{\text{|}}}^{4}} = \alpha \rho - \sigma {{\rho }^{2}}.$$

(17)

Here, the coefficient α was defined above Eq. (8) and  is related to the Kerr nonlinearity and σ = $- 20\pi \omega {{\chi }^{{(5)}}}{\text{/}}cn$, where ${{\chi }^{{(5)}}}$ is the fifth-order nonlinear optical susceptibility.

If ${{\chi }^{{(5)}}} < 0$ as often occurs [14], the optical nonlinear is saturated and $\sigma > 0$.

Taking into account Eq. (17), we consider the axisymmetric solution of system of Eqs. (15) and (16) in the cylindrical coordinates $r = \sqrt {{{y}^{2}} + {{\xi }^{2}}}$ and ζ. Assuming that

$$\varphi = \frac{c}{{n\omega }}gz = \frac{c}{{n\omega }}g\cos \theta \zeta {\kern 1pt} {\kern 1pt} ,$$

(18)

where g is a positive constant, we have ${{\nabla }_{2}}\varphi = 0$. Then, $\partial \rho {\text{/}}\partial \zeta = 0$ follows from Eq. (15). Thus, the variable ρ depends only on y and ξ.

In the case under consideration, Eq. (16) takes the form

$${{\Delta }_{2}}Q = \frac{1}{{R_{0}^{2}}}Q - \frac{{2n\omega }}{c}(\alpha {{Q}^{2}} - \sigma {{Q}^{4}}),$$

(19)

where $Q = \sqrt \rho$,

$$\begin{gathered} \frac{1}{{R_{0}^{2}}} = {{q}^{2}} + \frac{{2n\omega }}{c}(g\cos \theta + q\sin \theta ) \\ \approx \frac{{2n\omega }}{c}(g\cos \theta + q\sin \theta ). \\ \end{gathered} $$

(20)

Here, ${{q}^{2}}$ is neglected because q, $g \ll n\omega {\text{/}}c$ (see Eqs. (13) and (20)) in the paraxial and slowly varying envelope approximations.

Equation (19) at $R_{0}^{2} > 0$ has localized solutions vanishing at infinity $(r \to \infty )$ [14]. In this case, R₀ is the characteristic size of the localization region on the (y, ξ) plane. The light energy is not localized along the transverse x axis because of the tilt of wavefronts (see the second term on the left-hand side of Eq. (5)). Thus, the spatiotemporal soliton of Eq. (5) with tilted wavefronts has the shape of a cigar extended in the direction orthogonal to the velocity and to the plane of polarization of the soliton (Fig. 1).

We now analyze the stability of this soliton. To this end, we consider the axisymmetric self-similar solution of Eq. (15) [21–23]

$$\rho = {{\rho }_{0}}\frac{{R_{0}^{2}}}{{{{R}^{2}}}}G\left( {\frac{r}{R}} \right),\quad \varphi = f(\zeta ) + \frac{{{{r}^{2}}}}{{2R}}\frac{{dR}}{{d\zeta }}.$$

(21)

Here, ${{\rho }_{0}}$ is proportional to the intensity of the light energy on the central axis $(r = 0)$ of the spatiotemporal soliton (Fig. 1) at its equilibrium radius R₀, R(ζ) is the radius of this soliton, and f(ζ) and G(r/R) are a-rbitrary smooth functions.

Since the solution is localized on the (y, ξ) plane, the function G(r/R) can be approximated by the Gaussian [14]

$$G = {{e}^{{ - {{r}^{2}}/{{R}^{2}}}}}.$$

(22)

Then, on the right-hand side of Eq. (16),

$$\frac{{{{\Delta }_{2}}\sqrt \rho }}{{\sqrt \rho }} = \frac{{{{\Delta }_{2}}\sqrt G }}{{\sqrt G }} = - \frac{2}{{{{R}^{2}}}} + \frac{{{{r}^{2}}}}{{{{R}^{4}}}}.$$

Taking into account Eq. (17) and using the axial approximation [21], in which only the first two terms of expansion in the Taylor series in the parameter r²/R², $G \approx 1 - {{r}^{2}}{\text{/}}{{R}^{2}}$, ${{G}^{2}} \approx 1 - 2{{r}^{2}}{\text{/}}{{R}^{2}}$, are significant in the expression for G, substituting Eqs. (21) and (22) into the left-hand side of Eq. (16), and equating the coefficients of r⁰ and r² on the left- and right-hand sides of Eq. (16), we obtain

$$\begin{gathered} \frac{{df}}{{d\zeta }} = - \frac{c}{{n\omega }}\left( {\frac{c}{{n\omega }} - \alpha {{\rho }_{0}}R_{0}^{2}} \right)\frac{1}{{{{R}^{2}}}} + \frac{c}{{n\omega }}\sigma \rho _{0}^{2}\frac{{R_{0}^{4}}}{{{{R}^{4}}}} \\ - \;\frac{1}{2}{{\left( {\frac{c}{{n\omega }}} \right)}^{2}}\left( {{{q}^{2}} + \frac{{2n\omega }}{c}q\sin \theta } \right), \\ \end{gathered} $$

(23)

$$\frac{{{{d}^{2}}R}}{{d{{\zeta }^{2}}}} = - \frac{{\partial U}}{{\partial R}},$$

(24)

$$U = \frac{c}{{2n\omega }}\left( {\frac{c}{{n\omega }} - 2\alpha {{\rho }_{0}}R_{0}^{2}} \right)\frac{1}{{{{R}^{2}}}} + \frac{c}{{n\omega }}\sigma \rho _{0}^{2}\frac{{R_{0}^{4}}}{{{{R}^{4}}}}.$$

(25)

Equation (24) is formally similar to the equation of motion of a Newtonian particle with unit mass in an external force field with the potential energy given by Eq. (25).

The stable spatiotemporal soliton should correspond to the local minimum of the function U(R). According to Eq. (25), this minimum is absent in the presence of only the focusing Kerr nonlinearity (σ = 0). Consequently, in this case, as in the absence of tilt of wavefronts [14], the spatiotemporal soliton cannot be formed. If σ = 0, the pulse is self-focused at $2\alpha {{\rho }_{0}}R_{0}^{2} > c{\text{/}}n\omega$ and is defocused otherwise. Using the expression for α and the relation between χ⁽³⁾ and n₂, we rewrite this inequality in the form of the following condition on the pulse intensity:

$$IR_{0}^{2} > \frac{{{{c}^{2}}}}{{2{{n}^{3}}{{\omega }^{2}}{{n}_{2}}}}.$$

(26)

It is noteworthy that the left-hand side of Eq. (26) is not proportional to the power of the soliton, as in the case of light pulses without tilt of wavefronts. The reason is that R₀ is the radius of the sections of the pulse along the propagation of the pulse (Fig. 1). This radius can be estimated using Eqs. (14) and (7) at β = 0. Then, R₀ ~ v_gτ_pcotθ. The substitution of θ = 45° and τ_p ~ 10^–12 s gives R₀ ~ 10^–2 cm. In addition, Eq. (26) with the above estimates for the parameters of fused silica yields the intensity I > 10¹⁰ W/cm².

According to Eq. (25), the function U(R) has a local minimum at σ > 0, i.e., at saturating nonlinearity. Consequently, the parameter σ can be expressed in terms of α and the saturation intensity I_s. Indeed, at saturating nonlinearity,

$$\begin{gathered} F({\text{|}}\psi {{{\text{|}}}^{2}}) = \frac{{\alpha {\text{|}}\psi {{{\text{|}}}^{2}}}}{{1 + I{\text{/}}{{I}_{{\text{s}}}}}} \approx \alpha {\text{|}}\psi {{{\text{|}}}^{2}}\left( {1 - \frac{I}{{{{I}_{{\text{s}}}}}}} \right) \\ = \alpha {\text{|}}\psi {{{\text{|}}}^{2}}\left( {1 - \frac{{c{\text{|}}\psi {{{\text{|}}}^{2}}}}{{2\pi n{{I}_{{\text{s}}}}}}} \right) = \alpha {\text{|}}\psi {{{\text{|}}}^{2}} - \sigma {\text{|}}\psi {{{\text{|}}}^{4}}. \\ \end{gathered} $$

Therefore,

$$\sigma = \frac{{c\alpha }}{{2\pi n{{I}_{{\text{s}}}}}}.$$

(27)

The condition ${{(\partial U{\text{/}}\partial R)}_{{R = {{R}_{0}}}}} = 0$ of minimum of Eq. (25) gives the quadratic equation $\rho _{0}^{2} - \frac{\alpha }{{2\sigma }}{{\rho }_{0}} +$ $\frac{c}{{4n\omega \sigma R_{0}^{2}}} = 0$. This equation with Eq. (27) has real roots under the condition $R_{0}^{2} > \frac{{2{{c}^{2}}}}{{\pi {{n}^{2}}\omega \alpha {{I}_{{\text{s}}}}}}$. The substitution of the expression for α presented in the first sentence of Section 3 reduces this condition to the form

$${{R}_{0}} > {{R}_{{\min }}} = \frac{{2c}}{{n\omega \sqrt {n{{n}_{2}}{{I}_{{\text{s}}}}} }}.$$

(28)

Substituting I_s ~ 10¹² W/cm² [14] and other parameters for fused silica given above, we obtain R_min ~ 10^–3 cm.

Conditions (26) and (28) are key for the possibility of formation of spatiotemporal solitons with tilted wavefronts with the shape of cigars extended in the directions perpendicular to their propagation direction.

According to Eq. (26) at R₀ = R_min, I > I_s/8. If R₀ > R_min, condition (26) for the intensity is less stringent. Thus, the conditions presented above are in satisfactory agreement with the used approximations.

5 CONCLUSIONS

To summarize, this study has shown that the tilt of wavefronts of the optical pulse can significantly affect the character of formation and propagation of temporal and spatiotemporal solitons. The diffraction broadening of the pulse along phase wavefronts in the projection on the direction of the group velocity looks like its dispersion spreading. This formally leads to the redefinition of the second-order GVD coefficient in the form of Eq. (7). Thus, the dispersion of the group velocity can be controlled by varying the tilt angle of wavefronts. It is important that the additive caused by diffraction GVD is negative. As a result, the effective GVD can become anomalous. This in turn promotes the formation of solitons in media with focusing Kerr nonlinearity at β > 0 when temporal and spatiotemporal solitons with untilted wavefronts cannot be formed. Such a situation occurs, e.g., at the propagation of laser pulses of the visible spectral range in fused silica. In these cases, selecting the tilt angle such that β_eff < 0, one can create favorable conditions for soliton propagation regimes. The possibility of the soliton regime at β = 0 can be considered as a particular case. Here, we discuss dissipationless solitons with tilted wavefronts.

Owing to the tilt of wavefronts, spatiotemporal solitons have the shape of a cigar strongly extended along group fronts perpendicular to the plane of polarization. At the same time, they are localized in all directions perpendicular to the direction of extension of the soliton.

Here, the stability of spatiotemporal solitons with respect to azimuthal perturbations [24] and to bending perturbations corresponding to bending of group wavefronts [25–28] is not studied and will be considered elsewhere.

In this work, the possibility of formation of nonresonant quasimonochromatic solitons with tilted wavefronts has been analyzed. A similar study of resonant solitons in the self-induced transparency regime, in particular, the study of the possibility of formation of resonant light bullets with tilted wavefronts, is also of interest.

For optical solitons with a short time duration, it is necessary to take into account higher order GVD. In these cases, the tilt of wavefronts should be of significant importance, in particular, for few-cycle light pulses.