Quantum wells and thin films based on HgTe have attracted unabated interest in condensed matter physics for more than ten years. This interest is related to the recent emergence of a new class of physical objects with striking properties called two-dimensional (2D) and three-dimensional topological insulators (TIs) and their first implementation in HgTe quantum wells [1].

Since the concept of 2D TIs was originally put forward [2, 3], a large number of theoretical predictions were confirmed and remarkable novel effects were discovered. In particular, ballistic transport on a microscopic scale was observed [1], the edge character of transport in samples of macroscopic size was demonstrated via nonlocal transport measurements [4–7], and the possibility of the existence of a 2D TI even in narrow-gap quantum wells was shown [6]. Considerable advances have been made in the spin polarization studies of edge states. To this end, measurements of injection/detection between a conventional 2D metal and a quantum spin Hall state were used [8], the local magnetic fields formed by edge currents were investigated by atomic force microscopy [9, 10], and the generation of spin-polarized currents under the impact of circularly polarized terahertz radiation [11] and in structures with ferromagnetic tunneling contacts [12] was demonstrated.

However, neither have ballistic edge channels in 2D TIs longer than a few microns been realized, nor have unambiguous conclusions on the main mechanism of electron scattering in these channels been reached. It was shown recently that a very low magnetic field weakens topological protection and leads to Anderson localization at low temperatures, which is manifested in the exponential growth of the edge-channel resistance [13]. Still, this cannot explain the lack of ballistic behavior in the general case. The most realistic idea is to take into account the interaction of inhomogeneities in the 2D bulk (electron or hole droplets) with edge channels [14], but this issue is insufficiently studied experimentally because localization can take place in the bulk as well [15]. Here, we extended considerably the approach presented in [7] to the case where the ratio between the characteristic 2D and one-dimensional conductances varies by two orders of magnitude as the temperature is varied from 0.1 to 10 K.

The samples under study were based on 11.5-nm-thick Cd0.06Hg0.94Te quantum wells grown by molecular-beam epitaxy on a (013)-oriented GaAs substrate (Fig. 1a). To investigate the transport response, these structures were processed into ten-contact Hall bars equipped with a TiAu gate. The middle part of these bars represents three consecutive sections with a width of 50 μm and lengths of 100, 250, and 100 μm (Fig. 1b). The resistance was measured in the local and nonlocal geometries using the four-terminal technique, so that the voltage drop and the current flowing through the sample were measured simultaneously. One of the features of this study is wide ranges of temperatures (from 80 mK to 20 K) and resistances (from 1 Ω to hundreds of megaohms). For this reason, in order to avoid sample heating and, in addition, to increase the signal-to-noise ratio, we utilized both the layouts with either a current source (with driving currents of 0.1–10 nA) or a voltage source (with driving voltages of 1–10 mV) modulated at frequencies of 1‒12 Hz.

Fig. 1.
figure 1

(Color online) (a) Cross-sectional outline of the structure under study. (b) Layout of the Hall bar coated with a metallic gate. Spacings between the potentiometric contacts and edge lengths are shown at the bottom and top of the figure, respectively. (c) Dependences ρxx(Vg) in zero magnetic field at a temperature of T = 4.7 K and ρxy(Vg) in a field of B = 3 T at T = 1 K. The vertical arrow labeled \(V_{{\text{g}}}^{0}\) marks the peak in ρxx and, at the same time, the charge-neutrality point.

Full size image

Figure 1c shows the resistivity ρxx measured as a function of the gate voltage Vg. This dependence exhibits a characteristic peak at the charge-neutrality point, which occurs at a voltage \(V_{{\text{g}}}^{0}\) = –2.1 V. Higher and lower voltages correspond to the electron and hole regions, respectively, which is confirmed by the measurements of the Hall resistivity ρxy, also plotted in Fig. 1c. One can clearly see the quantum Hall effect plateaus with filling factors ν = 1–3 for electrons. The highest carrier mobilities are 250 × 103 and 103 cm2/(V s) for electrons and holes, respectively.

We now consider the behavior of the system near the charge-neutrality point. For convenience, let the gate voltage be measured from \(V_{{\text{g}}}^{0}\), i.e., \(V_{{\text{g}}}^{*}\) ≡ Vg – \(V_{{\text{g}}}^{0}\). At \(V_{{\text{g}}}^{*}\) = 0 and temperature T = 4.7 K, ρxx = 82 kΩ/□, which is higher than h/e2. This fact indicates a dielectric behavior and the existence of an energy gap between the valence and conduction bands, which means that the thickness of the quantum well is larger or smaller than its critical value.

Let us analyze the evolution of the dependences ρxx(Vg) with temperature in the range from 80 mK to 21 K (Fig. 2a). At the charge-neutrality point and in its vicinity (i.e., in the range of \(V_{{\text{g}}}^{*}\) from –1 to 1 V), the system demonstrates dielectric behavior: the resistivity increases from 5 to 500 kΩ/□ upon cooling from 21 to 1 K. With a further decrease in the temperature, the peak resistivity is saturated, increasing further by only 15% (i.e., to 600 kΩ/□) at the lowest temperature (80 mK). The peak itself becomes broader with respect to the gate voltage and a flat segment is formed at its top, indented with random quantum fluctuations of the resistivity. This behavior of ρxx(Vg) is typical of a 2D TI: the saturation of the temperature dependence at T < 1 K corresponds to the transition from the bulk conductivity regime to the conductivity through topological edge channels. We note that the resistivity determined per unit area becomes irrelevant in the edge transport regime, because the physically meaningful quantity in this case is the edge length L, which equals about 200 μm for the section of the Hall bar we used (Fig. 1b). In the approximation where the edge channel resistance depends linearly on its length [7], we find that the mean free path equals lB = L[(h/e2)/2Rloc = 2.4 × 106 Ω)] = 2.2 μm. This value agrees with those obtained for other typical samples based on HgTe quantum wells.

Fig. 2.
figure 2

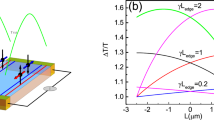
(Color online) Gate-voltage dependences of the (a) local resistivity ρxx(\(V_{{\text{g}}}^{*}\)) and (b) nonlocal resistance \(R_{{{\text{nonloc}}}}^{{{\text{near}}}}(V_{{\text{g}}}^{*})\) for B = 0 and T = 0.08, 0.13, 0.28, 0.53, 0.8, 1.1, 1.8, 2.6, 3.6, 5.2, 6.8, 8.6, 10, 12, 15, and 21 K. (c) Dependences ρxx(B) measured near the charge-neutrality point (\(V_{{\text{g}}}^{*}\) = –0.1 V) at the same temperature. The insets show the arrangement of current and potentiometric contacts (red and blue, respectively).

Full size image

To check that the investigated quantum well features nonlocal conductivity, which is a property characteristic of 2D TIs, we investigated the nonlocal transport response in two different configurations where the current and potentiometric contacts were separated by distances of 100 μm (see Fig. 1b and the inset in Fig. 2b) and 350 μm (not shown). The results obtained in the two cases are in qualitative agreement and fit quantitatively into a single physical picture. To save space, we omit the data for the 350-μm configuration (but they are taken into account in simulations, Figs. 3c and 3d). The dependences of the nonlocal resistance \(R_{{{\text{nonloc}}}}^{{{\text{near}}}}(V_{{\text{g}}}^{*})\) for the first configuration of the contacts are shown in Fig. 2b. At first glance, these curves reproduce the gate-voltage dependences of ρxx, but there are also important differences. At high temperatures (T > 5 K), the nonlocal resistance is several orders of magnitude lower than the local resistance, which is typical of systems with bulk conductivity. However, as the temperature is reduced, the peak nonlocal resistance becomes comparable to and then even higher than the local resistance and is as high as 2.8 MΩ at T = 80 mK. This value is in fairly good agreement with a theoretical value of 4 MΩ calculated using the actual length of topological channels (Fig. 1b) and the mean free path of lB = 2.2 μm. The 30% difference is related to the impact of disorder in the system [5] and, to a lesser extent, to the imperfection of optical lithography (asymmetric placement of the gate with respect to the center of the Hall bar).

Fig. 3.
figure 3

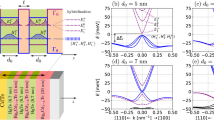
(Color online) (a) Schematics of current flows for (top part) bulk and (bottom part) edge transport regimes in the (left part) local and (right part) nonlocal geometries. (b, d) Fits of the gate-voltage dependences of the local resistance Rxx and the nonlocal resistances \(R_{{{\text{nonloc}}}}^{{{\text{near}}}}\) and \(R_{{{\text{nonloc}}}}^{{{\text{far}}}}\) measured with the current and potentiometric contacts separated by distance of 100 and 350 μm, respectively. The temperature is T = (b) 0.5 and (d) 1.5 K. Circles and solid lines show experimental points and simulation results, respectively. (c) Two scattering mechanisms taken into account in the model. Intra-edge-state scattering (γ) requires the presence of electron–hole droplets where spin flips take place. For scattering into the bulk (g), spin flips is inessential.

Full size image

The temperature dependences of the peak values of the local and nonlocal resistances can be qualitatively understood in the following way. The total conductance of the system is the sum of the contributions from bulk carriers and edge topological channels (see Fig. 3a, upper and lower images, respectively). At low temperatures, there are no delocalized bulk carriers near the charge-neutrality point, and the conductance is determined solely by edge transport. As the temperature increases, charge carriers are activated and the bulk conductance increases. In the local geometry, this leads to a gradual decrease in the measured resistance because the bulk and edge conductances contribute additively. At temperatures exceeding 2 K, bulk conductance becomes dominant, while the contribution from edge conductance is minor. For the nonlocal resistance, an increase in the temperature leads to much more abrupt effects, because the bulk shunts the edge conductance. For the same reason, the peak half-width of the nonlocal resistance, which is determined by the onset of band filling in the bulk, is considerably smaller than that in the local resistance (see Figs. 3c and 3d).

Another confirmation that the system under study is a 2D TI was obtained from the investigation of its response in a magnetic field. It was shown recently that even a weak magnetic field of a few millitesla leads to the breaking of topological protection from backscattering in edge channels and to the onset of Anderson localization [13]. The results of our measurements of ρxx(B) at \(V_{{\text{g}}}^{*}\) = –0.1 V, which are shown in Fig. 2c, agree with this model. At temperatures below 1 K, we observe positive magnetoresistance that depends exponentially on the magnetic field. The absolute maximum is attained in a field of 0.13 T and equals 53 MΩ/□, which corresponds to 106 MΩ. Upon the normalization by an edge length of 200 μm, we obtain a considerably lower one-dimensional resistivity than that reported in [13], where, under the same conditions, the same edge resistance was obtained for a channel as short as 38 μm.

The obtained temperature dependences were analyzed quantitatively using computer simulations of current flow based on the model model introduced in [7] and adapted here according to the problem at hand. The model involves two conduction channels, i.e., the bulk and the edge ones. The electrostatic potential distribution was specified separately for the edges and the bulk of the sample and was discretized with a step of 1 μm. It was assumed that the bulk conductivity is given by the Drude term σbulk. The conductance of each edge channel was originally set at e2/h, but was allowed to decrease owing to scattering processes. The latter were described by phenomenological parameters γ and g, which determine the probabilities of scattering per unit edge length within the edge channel and into the bulk, respectively (Fig. 3b).

The following procedure was used to fit the data obtained for each temperature. The values of γ and g served as fitting parameters. Three experimental dependences were fitted, one is R-local(Vg) and two are Rnonloc(Vg), measured in the configurations with the current and potentiometric contacts spaced by 100 and 350 μm, respectively (see Figs. 3c, 3d). At the first stage of the fitting procedure, σbulk(Vg) was calculated by the formula 1/Rlocal(Vg) = Wσbulk(Vg) /L + 1/Redge, where L and W are the length and width of the investigated segment of the sample, respectively, and Redge is the equivalent resistance of its edges. To determine the latter quantity, we assume that it depends weakly on the temperature and gate voltage (at least near the charge-neutrality point) and that σbulk → 0 when T → 0. In so far as the crossover between the bulk and edge types of transport takes place at a temperature of about 1 K, we have \({{R}_{{{\text{edge}}}}} \ll W{\text{/}}L \times \sigma _{{{\text{bulk}}}}^{{ - 1}}\) at T = 80 mK. Therefore, \({{R}_{{{\text{edge}}}}} = \langle {{R}_{{{\text{local}}}}}{\kern 1pt} {{|}_{{T = 80\,{\text{mK}}}}}\rangle \), where \(\langle \ldots \rangle \) designates averaging with respect to Vg (this averaging is required because of quantum fluctuations of the resistance, which are not considered in the model). Next, the optimum pair of parameters γ and g that minimize the sum of the squared differences between the experimental and theoretical dependences was determined. The differences calculated for the nonlocal dependences were assigned a weight equal to the ratio R-local/Rnonloc at the charge-neutrality point.

Examples of the experimental data fits for temperatures of 0.5 and 1.5 K are shown in Figs. 3c and 3d, respectively. Good agreement between the model and experiment is obtained for both temperatures. It is essential that three curves are fit with the same set of the parameters g and γ because both fitting curves for Rnonloc(Vg) are sensitive to both parameters g and γ, but the magnitude of the effect depends on the distance between the current and potentiometric contacts. Owing to the simultaneous fit of the nonlocal response in two different contact configurations, the obtained parameters are unambiguous and the fit is self-consistent. The half-width of the peaks on the fitting curves is determined by the behavior of σbulk(Vg) and is almost independent of g and γ.

Next, let us proceed to the main results of this study. Figure 4a shows the temperature dependences of (a) the maximum measured local and nonlocal resistances and (b) the fitting parameters g and γ obtained from the fits at the same temperatures. The experimental curves show clear evidence of the crossover from the edge transport regime, where the temperature dependence is nearly absent, to the bulk transport regime, where the resistance varies by several orders of magnitude. No characteristic activation energy can be obtained from these curves since they do not feature clearly manifested linear segments (in the given coordinates) in the high-temperature region. This occurs probably because the energy gap is of the same order of magnitude as the scale of disorder in the system.

Fig. 4.
figure 4

(Color online) (a) Peak values of the local and nonlocal resistances \(R_{{xx}}^{{\max }}\) and \(R_{{{\text{nonloc}}}}^{{\max }}\), respectively, versus the inverse temperature. The inset shows the region from 0 to 0.5 K–1 on an expanded scale. (b) Inverse fitting parameters 1/g and 1/γ defining the partial mean free paths of topological electrons related to their scattering into the bulk and within edge states, respectively, versus the inverse temperature. Fitting the dependence of 1/g(1/T) with an activation formula A exp(–Δ/2kT) makes it possible to determine the mobility gap Δ = 0.7 meV.

Full size image

Let us now analyze the behavior of the fitting parameters g and γ. Figure 4b clearly shows that parameter γ is almost independent of the temperature, and γ–1 = 1.2 μm is of the same order of magnitude as the experimental estimate for the ballistic length lB = 2.2 μm. The temperature dependence of g is completely different: its value increases by three orders of magnitude when the temperature changes from 0.5 to 5 K, and its behavior in this range is well described by an activation curve Ae–Δ/2kT with the energy parameter Δ = 0.7 meV. At higher temperatures, the fit ceases to be unambiguous because the nonlocal resistance measured over the farther section becomes too small. In so far as the parameter g determines the probability of scattering out of an edge state into a delocalized state in the bulk, the energy Δ is just the mobility gap of the system under study. We note that the described method to determine its value is more correct than direct analysis of the experimental data presented in Fig. 4a. The resulting value of Δ turns out to be orders of magnitude smaller than that obtained for an 8-nm-thick HgTe quantum well (30 meV) and significantly smaller than the one in a 14-nm well (3 meV). Almost in the entire temperature range, the value of 1/g exceeds 1/γ by orders of magnitude, and at the lowest temperature, 1/g becomes as large as 100 mm. This means that, even at high temperatures when the bulk conductivity is dominant, the resistance of the edge channels is determined by scattering within these channels rather than by interaction with the bulk.

In summary, we have studied the transport response of a CdHgTe quantum well with a thickness of 11.5 nm. We have shown that the investigated quantum well represents a 2D TI characterized by a significantly smaller energy gap and higher carrier mobility than conventional HgTe-based 2D TIs. The experimental data have been analyzed by computer simulations. We have demonstrated that the probability of backscattering of topological electrons within the edge is nearly temperature-independent. On the contrary, the probability of scattering from edge channels into the bulk depends exponentially on the temperature. Fitting this dependence with a standard activation formula is the most accurate way to determine the mobility gap in the system under study and yields the value of Δ = 0.7 meV.