On the Percolation Regime of the Bulk Transport of the Bi_1.08Sn_0.02Sb_0.9Te₂S Topological Insulator

The formation of nanosized charge droplets in the bulk of a three-dimensional topological insulator Bi_1.08Sn_0.02Sb_0.9Te₂S was evidenced using electron spin resonance. Since electrons and holes are “locked” in these droplets far apart from each other, their participation in bulk conductivity is possible only due to thermal activation or to variable range hopping. Our transport measurements give evidence that at relatively high temperatures conduction follows the activation behavior with the activation energies which due to percolation may be much smaller than the half of the band gap. We also demonstrate that the variable range hoping replaces the activated transport at sufficiently low temperatures.

INTRODUCTION

The three-dimensional (3D) topological insulators (TIs) have very interesting gapless surface states [1–3] which exhibit novel quantum features such as spin–momentum locking and the absence of backscattering. On the other hand, the majority of the 3D TIs which have been identified, are rather poor insulators in the bulk, so that the properties of the surface are obscured in transport measurements. For this reason, achieving a bulk-insulating state remains an attractive field of research [4–14].

Moreover, the studies of TI are currently marked by a growing interest to the origin of strong impact of various defects and local charge inhomogeneities [15–19] existing in the insulating region between conducting surfaces or edges on the fundamental properties of surface current carriers.

An important issue is the detection and analysis of such inhomogeneities in real three-dimensional TIs, where their presence seems also to be very probable (if not inevitable). The fact is that complete suppression of bulk conductivity in them is achieved by compensating for current carriers by adding to their structure a small amount of impurity donor ions, in the case where it is necessary to “neutralize” holes or acceptors when it comes to “neutralizing” electrons. As a result, charged defects appear in the structure giving rise to local distortions of the band gap, which are anomalously strong when the screening is suppressed due to the small number of current carriers. This circumstance can lead to the appearance in the sample volume of 3D nanosized charge droplets (puddles) known in the physics of semiconductors [14, 20], and of strongly correlated 2D electron systems [21], manganites [22], etc.

In this regard, the role of various local methods in studying the properties of TI has significantly increased. One of the promising tools for solving such problems is the electron spin resonance (ESR), which can be used to study local inhomogeneities in the distribution of charge and spin excitations.

The main aim of the present paper is to study the local charge inhomogeneities in the insulating region between conducting surfaces of the 3D topological insulator Bi_1.08Sn_0.02Sb_0.9Te₂S. We use the ESR data elucidating the distribution of the local charge inhomogeneities together with the resistivity measurements in order to investigate their impact on the bulk transport properties of the compound.

EXPERIMENTAL PROCEDURE AND RESULTS

1. Our investigations of 3D TI were carried out with the isostructural version of Bi telluride compound Bi_1.08Sn_0.02Sb_0.9Te₂S (BSSTS), which is known to be one of the best 3D TI. The studied single crystals were grown using the procedure described in [23]. It is worth noting that the compensation of the last of native defects present was achieved through 1% Sn substitution for Bi. The comprehensive characterization of the grown single crystals revealed [24, 25] that their structure, transport and magnetotransport properties were similar to those published in [23]. The bulk BSSTS is highly insulating. Resistivity increases exponentially with decreasing T, attains a maximum value (up to ~60 Ω cm) at ~100 K, and starts decreasing with decreasing T. This decrease indicates that the resistivity of the insulating bulk material is short-circuited by the metallic surface carriers. The bulk band gap is equal to 330 meV. The carrier densities $(n)$ are as low as ~3 × 10¹⁴ cm^–3.

2. The surface of samples was investigated by scanning tunneling spectroscopy using Ultra Low Temperature and High Magnetic Field STM Unisoku USM 1300. The differential conductance $(dI{\text{/}}dV)$ was measured along the 24 lines on the surface which were shifted from each other by 0.5 nm. The corresponding surface map obtained at temperature of 2 K is shown in Fig. 1. Then the conductance curves were averaged over all scanned lines. The arrows at averaged curve displayed in Fig. 2 point to the approximate positions of the top of the bulk valence band (vbt), bottom of conduction bands (cbb), Dirac point (DP), Fermi level $({{E}_{{\text{F}}}})$. See the corresponding cartoon scheme in Fig. 3.

Fig. 1.

(Color online) STM map of the differential conductance $(dI{\text{/}}dV)$ measured along the parallel lines on the surface which were shifted from each other by 0.5 nm.

Fig. 2.

(Color online) Conductance curve averaged over 0.5 nm long lines (2) in comparison with the raw curve (1). The arrows at the averaged curve indicate the approximate positions of the top of the bulk valence band and the bottom of conduction bands (vbt and cbb) and the position of the Dirac point (DP) together with Fermi level (E_F).

Fig. 3.

(Color online) Cartoon of the band structure for studied BSSTS samples.

We will use the estimated parameters of the BSSTS band structure for the analysis of the transport properties of the studied samples.

3. Let us now proceed to the discussion of ESR data since they provide a crucial insight to the character of the local inhomogeneities in the bulk of BSSTS. The ESR spectra were recorded using the standard X‑band (9.2–9.6 GHz) spectrometer Bruker BER-418s in the temperature range from 1.4 up to 100 K. (The typical samples for ESR measurements were crystalline slices with a thickness ~0.15–0.2 mm.)

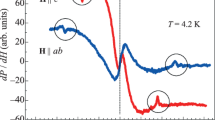
The typical ESR signal consisted of two lines observed at fields in the region between 150 and 250 Oe (the low- and high-field peaks correspond to holes and electrons, respectively). The positions of these signals strongly depend on the orientation of the magnetic field relative to the c axis which is perpendicular to the basal ab plane of the crystal (see Fig. 4). Electron spin resonance in such weak magnetic fields corresponds to unusually large values of the g-factors of charge carriers [26–28], which indicates a strong spin–orbit interaction characteristic of topological insulators.

Fig. 4.

(Color online) Angular dependence of the ESR spectra on the orientation of the magnetic field relative to the c axis (characterized by the angle θ) which clearly reveals the superposition of two different ESR lines corresponding to holes and to electrons.

Let us turn now to the angular dependence (Fig. 4) of the spin resonance spectra on the orientation of the magnetic field relative to the c axis (characterized by the angle θ), which clearly reveals the superposition of two different ESR lines corresponding to holes and electrons (see [29] for the details). From the analysis of the observed spectra using for the angular dependence of $g$-factor of each superimposed line the standard expression ${{g}^{2}} = {{g}_{\parallel }}2{{\cos }^{2}}{\kern 1pt} \theta + g_{ \bot }^{2}{{\sin }^{2}}{\kern 1pt} \theta$, we found that for holes ${{g}_{ \bot }} = 28.3 \pm 1$; ${{g}_{\parallel }} = 47.4 \pm 1$, and for electrons ${{g}_{ \bot }} = 26.4 \pm 1;$ ${{g}_{\parallel }} = 44.7 \pm 1$.

The strong temperature dependence of the observed lines should be specially noted: the intensity of lines rapidly decreases with increasing temperature (Fig. 5). At temperatures above 15 K, the lines became unobservable.

Fig. 5.

(Color online) Temperature dependence of the integral intensity of the ESR signal for Bi_1.08Sn_0.02Sb_0.9Te₂S compound.

Let us proceed to the analysis of the integral signal intensity (Fig. 5), which, is known to correspond to the magnetic susceptibility of the system of spins responsible for the resonance signal. Instead of the temperature independence expected in accordance with the Pauli law, the integral intensity of the spin resonance signal from the charge carriers grows rapidly upon lowering temperature in a way similar to Curie-like dependence. For the system without any local magnetic moments such an unusual behavior may be considered as indication that the bulk charge carriers are arranged into the ensemble of nanosized “metal” particles randomly distributed in the bulk of sample [30, 31].

The smallness of the particles volume results in a pronounced discreteness of the electronic levels, which can give rise to anomalous properties of small particles in comparison with the properties of a bulk metal. The particles size dispersion, shape differences and uncontrollable imperfections, including the roughness of their surface, make the distribution of levels in the ensemble of small metallic particles completely random. Therefore, the average distance between electronic levels in a particle can be found using the usual density of states, ν, at the Fermi level for bulk metals [30, 31]

$$\nu = Vm{\text{*}}{{p}_{0}}{\text{/}}2{{\pi }^{2}}{{\hbar }^{3}},$$

(1)

where V is the volume of the particle, m* is the effective mass of carriers, ${{p}_{0}}$ is the boundary momentum.

It was found [31], that for such small “metal” particles (hereafter we will call them droplets), a quantized spectrum is realized, in which the distance between levels exceeds ${{k}_{{\text{B}}}}T$. The average distance between the levels $\delta E = 1{\text{/}}\nu$ has a finite value and according to Eq. (1) depends on the volume of the particles V. For $\delta E < {{k}_{{\text{B}}}}T$ the temperature dependence of susceptibility is described by the Pauli law, whereas for $\delta E > {{k}_{{\text{B}}}}T$ it is given by Curie law.

The crossover temperature ${{T}_{{{\text{cr}}}}}$ separating these regimes makes it possible to estimate the typical size of droplets $(\sim {\kern 1pt} {{V}^{{1/3}}})$. Using ${{T}_{{{\text{cr}}}}}\sim 10{-} 20$ K, ${{p}_{0}}\sim 0.03\hbar$ Å^–1, $m{\text{*/}}{{m}_{0}}\sim 0.1{-} 0.5$, we obtain that the size of electron and hole droplets ${{R}_{e}}$, ${{R}_{h}}$ is about 10–20 nm. Thus, the analysis of the integral signal intensity together with other ESR data gives evidences in favor of charge droplets formation.

The origin of charge droplets is following. The suppression of bulk conductivity in TI is achieved by compensating the charge carriers by adding to the structure a small amount of impurity donor ions, in the case where it is necessary to “neutralize” holes (or acceptors when it comes to “neutralizing” electrons). As a result, charged defects appear in the structure giving rise to local distortions of the band gap (see Fig. 6, adopted from [14, 20]), which are anomalously strong when the screening is suppressed due to the small number of charge carriers [20]. Due to such distortions a situation may arise when the top of the valence band can locally rise above the chemical potential. In this case the empty states form a kind of hole droplet. If the bottom of the conduction band locally sinks below the chemical potential, the electrons filling the formed cavity create an electron droplet.

Fig. 6.

(Color online) Inhomogeneities of the band structure along the coordinate R. The upper straight line is the bottom of the conduction band ${{E}_{c}}$, the bottom is the ceiling of the valence band ${{E}_{v}}$. The bold curved lines correspond to the deformed boundaries of the band gap. The filled areas under the chemical potential μ correspond to the electron droplets, the filled areas bounded from below correspond to the hole droplets, ${{R}_{{\text{g}}}}$ is the scale of the gap variation, and ${{R}_{e}}$ and ${{R}_{h}}$ are the sizes of electron and hole droplets, respectively. The energies ${{E}_{e}}$ and ${{E}_{h}}$ correspond to the percolation levels for electrons and holes, respectively.

4. The transport measurements with the BSSTS single crystals were carried out in the temperature range from 4 up to 300 K. Resistivity increases exponentially with decreasing T, attains a maximum value (up to ~60 $\Omega$ cm) at ~100 K, and starts decreasing with decreasing T. Below ~100 K, the transport is understood as a parallel connection of an insulating component characterized by a 3D VRH behavior and a “metallic component.” At low temperatures the resistivity of the insulating bulk material is short-circuited by the metallic surface carriers.

In order to analyze and to compare the temperature dependencies of different samples we take into account that all of them have the same magnitude of the band gap E_g between the top of the valence band and the bottom of the conduction band. From our STM measurements, we have E_g = 330 meV. (ARPES measurements [23] give E_g = 350 meV.) At relatively high temperatures the bulk conduction due to electrons and holes follows the activation behavior with resistivity $\rho = {{\rho }_{0}}\exp (\Delta {\text{/}}{{k}_{{\text{B}}}}T)$. Note, that for the fully compensated semiconductor one should expect for the thermal activation energy Δ = E_g/2.

However, some time ago the numerical calculations [14] revealed that at high temperatures the resistivity may be activated with relatively small activation energy in comparison with E_g/2. The point is that at T < E_g electrons optimize their conductivity by hopping between impurities that are energetically close to the Fermi level. The activation energy can be understood as the resulting percolation level for hopping at the nearest-neighboring sites. In other words, if electrons are activated only to those sites, then precisely at $\Delta = 0.17{{E}_{{\text{g}}}}$ there exists an infinite conduction pathway for electrons comprised of hops of length between nearest-neighboring distance. In a heavily doped semiconductor this energy is equivalent to the activation energy of electrons from the Fermi level to the conduction band mobility edge ${{E}_{e}}$. Since this finding is in agreement with some of the old generation of TI [12], it is tempting to verify if this behavior is valid for the newer TIs.

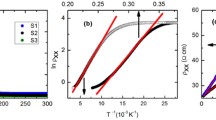
Let us begin from the resistivity of BSSTS sample with the largest maximal resistivity (~60 Ω cm). Its temperature dependence, shown in Fig. 7, reveals the thermal activation from the Fermi level to the bottom of the conduction gap with Δ = 165 meV. Here the concentration of droplets is too small to provide the conductivity via percolation. At sufficiently low temperatures (~100 K) electrons and holes can tunnel between the droplets, so that variable range hopping (VRH) replaces activated transport. In the low temperature limit the resistivity is expected to obey the Efros–Shklovskii (ES) law [14, 20] $\rho = {{\rho }_{0}}\exp \{ ({{T}_{{{\text{ES}}}}}{\text{/}}T{{)}^{{1/2}}}\}$, where ${{T}_{{{\text{ES}}}}}$ is the characteristic ES temperature. For the BSSTS we estimated ${{T}_{{{\text{ES}}}}} \sim 3200$ K, and the crossover to VRH ES regime takes place at 60–70 K.

Fig. 7.

(Color online) Temperature dependence of the Bi_1.08Sn_0.02Sb_0.9Te₂S transport for sample with the maximal resistivity ~60 $\Omega$ cm: (a) the resistivity ${{\rho }_{{xx}}}$ versus T, inset: the resistivity versus 1/T; (b) the conductivity ${{\sigma }_{{xx}}}( = 1{\text{/}}{{\rho }_{{xx}}})$ versus ${{T}^{{ - 1/2}}}$, dashed line is fitting with ${{\sigma }_{{xx}}} \sim \exp \{ - {{({{T}_{{{\text{ES}}}}}{\text{/}}T)}^{{1/2}}}\}$ to the data.

In Fig. 8 we show resistivity and conductivity for the different sample with the smallest value of resistivity (~10 Ω cm) at the maximum. The percolation at large concentration of droplets proceeds from Fermi level to the band mobility edge ${{E}_{e}}$ with Δ = 60 meV and overcomes the thermal activation to the bottom of the conduction gap. And again at low temperatures (~50–60 K) electrons and holes start to tunnel between the droplets, so that VRH replaces activated transport and the crossover to the VRH ES regime takes place at 60–70 K.

Fig. 8.

(Color online) Temperature dependence of Bi_1.08Sn_0.02Sb_0.9Te₂S transport for sample with maximal resistivity ~10 $\Omega$ cm: (a) the resistivity ${{\rho }_{{xx}}}$ versus T, inset: the resistivity versus 1/T; (b) the conductivity ${{\sigma }_{{xx}}}( = 1{\text{/}}{{\rho }_{{xx}}})$ versus T^–1/2, dashed line is fitting with ${{\sigma }_{{xx}}} \sim \exp \{ - {{({{T}_{{{\text{ES}}}}}{\text{/}}T)}^{{1/2}}}\}$ to the data.

CONCLUSIONS

The contactless visualization of local charge and spin inhomogeneities using ESR of the bulk charge carriers revealed that the charge carriers, participating in the resonance represent a randomly spaced array of electron or hole droplets of nanoscale sizes. It is expected that charge carriers from these droplets don’t participate in the ordinary transport, since they cannot travel freely from one droplet to another.

Our transport measurements give evidence that for BSSTS at relatively high temperatures conductivity due to electrons and holes follows the activation behavior with resistivity $\rho = {{\rho }_{0}}\exp (\Delta {\text{/}}{{k}_{{\text{B}}}}T)$, but the corresponding activation energies (${{\Delta }_{e}}$ and ${{\Delta }_{h}}$) may be much smaller than the half of the band gap, E_g/2. Analysis of our data revealed, that ${{\Delta }_{e}}$ may be as low as ~60 meV. Note, that for our BSSTS samples E_g/2 = 165 meV and one obtains the estimate $\Delta = 0.18{{E}_{{\text{g}}}}$. This value is very close to the percolation limit for 3D continuous random potential [20], $\Delta = 0.17{{E}_{{\text{g}}}}$, providing the creation of an infinite conduction pathway for electrons comprised of hops of length between nearest-neighboring distance. Note, that the observed suppression of activation gap is possible only if the concentration of droplets exceeds the percolation limit [14, 20]. To conclude, we would like to mention, that the physical picture discussed above gives serious arguments in favor of percolation regime of the bulk transport in TI.

It is important, that at sufficiently low temperatures electrons and holes can tunnel between the droplets, so that variable range hopping replaces activated transport to provide the Efros–Shklovskii regime $\rho = {{\rho }_{0}}\exp \{ ({{T}_{{{\text{ES}}}}}{\text{/}}T{{)}^{{1/2}}}\}$.