INTRODUCTION

Unlike ordinary crystals of covalently bonded atoms, two-dimensional (2D) van der Waals heterostructures are characterized by an angle θ by which the layers can be twisted relative to each other [1, 2]. Variation of this angle provides the full control of the symmetry of the structure of two or more such layers and, consequently, of its properties. Currently, the study of the structure and properties of such materials is engaged in a new scientific direction—twistronics. Features of twisted heterostructures allow one to control the properties through easily accessible external parameters such as stacking type, twist angle, or layer strain. In such structures, it is possible to implement and control a large number of fundamental quantum models that are relevant in condensed matter physics, and they can be used to study strongly correlated physics and topology in quantum materials [3].

Recently, new 2D structures, Dnθ moiré diamanes [4–6], based on fully hydrogenated (or fluorinated) twisted bilayer graphene, which is transformed into a diamond-like layer with a moiré structure, have been considered. It was shown that they have unique features distinct from their diamane counterparts formed from untwisted graphene [7, 8]. Diamanes consisting of several such layers were studied theoretically and experimentally [8–10].

In this paper, the features of the atomic and electronic structures of diamond-like films formed from few-layer graphene containing up to four layers twisted in a special way at an angle of about 30° are considered.

RESEARCH METHOD

The VASP software package [11–13], which implements the electron density functional theory (DFT) method, was used to optimize the geometry of moiré diamanes and obtain their band structures and densities of electronic states. The exchange-correlation functional was calculated in the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) parameterization [14]. The ion–electron interaction was described using the projector augmented wave (PAW) method [15]. The cutoff energy of plane waves was 500 eV, and the periodic images were separated by a vacuum gap of at least 10 Å to exclude interaction between them. The structure was optimized to minimize the force acting on each atom to 10–4 eV. The DFT-D3 Grimm method [16] was used to describe the van der Waals interaction. To optimize the geometry of the structures, the Brillouin zone was partitioned according to the Monkhorst–Pack method [17] using a 5 × 5 × 1 k-point grid. Note that this technique underestimates the band gap; in particular, the experimental value for diamond is Eg = 5.47 eV [18], while the calculated one is Eg = 4.20 eV.

RESULTS AND DISCUSSION

A feature of the bilayer graphene structure with the moiré angle θ = 30° is the presence of intersections of С–С bonds of one layer with С'–С' bonds of another layer. During the diamane synthesis, the atoms forming these bonds cannot form interlayer bonds and they are preferred for the adsorption of hydrogen, fluorine, or molecules. The same feature is typical of bigraphene with moiré angles from 20° to 30°. The structure of diamanes based on bigraphene with θ = 27.8° and 29.4° is described in detail in [4].

To obtain a Dnθ(M) diamane from M-layered moiré graphene, it needs to be in a specific stacking. The second layer is rotated relative to the first one by an angle of θ and the third layer forms an AA-stacking with the second one. Such a stacking of three-layer graphene will be called 0θθ.

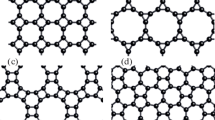
The formation of a three-layer diamane Dnθ(3) begins with the adsorption of adatoms, which can be performed by methods of experimental production of diamanes [8–10]. However, in order to prevent the formation of an energetically more favorable AA-diamane [7] from θθ layers, it is necessary to start hydrogenation only from the surface of the 0 layer. In this case, the graphene/diamone sandwich heterostructure or diamondol [19], i.e., a diamone with hydroxyl groups adsorbed on its surface instead of light atoms from 0θ bigraphene, is formed (Fig. 1a). This process is similar to the chemically induced phase transition from graphene to a new structure, which was considered earlier for the case of diamane formation from multilayer graphene [20]. Thus, Donθ moiré diamone contains chemically active sp2 atoms, which, after some time of exposure to the adsorption flow, should be covalently bonded to the atoms of the lower graphene layer, forming the Donθ(3) diamone (Fig. 1b). Donθ(3) also contains unsaturated bonds on the surface (Fig. 1b). A similar process of transformation of multilayer graphene in a conventional untwisted stacking was first considered in [19]. The difference is that, because of the similar stacking of the second and third layers, they must be connected by opposite pairs of C and C' atoms forming the so-called 2 + 2 cycles in the form of a “square” (Figs. 2b and 2с), which usually appear during the polymerization of С60 fullerenes [21].

Fig. 1.
figure 1

(Color online) Scheme of the diamane formation from a three-layer graphene structure 0θθ with the upper layer twisted at an angle θ relative to the lower bilayer with AA-stacking: (a) formation of the Donθ diamone from θ0 layers; (b) the further process of formation during the hydrogen adsorption from the side of the lower layer, which transforms into the Donθ(3) diamone; and (c) formed Dnθ(3) diamane. Fragments of the corresponding atomic structures are shown in the lower parts.

Full size image
Fig. 2.
figure 2

(Color online) Scheme of the diamane formation from four-layer graphene: (a) the AA-bilayer θθ (black) is twisted at an angle θ relative to the upper and lower (violet) layers at the beginning of the hydrogen (or fluorine) adsorption process, (b) formation from 0θ layers of the Donθ diamone lying on graphene bilayer 0θ, (c) hydrogen adsorption from the side of the fourth layer after the formation of the Donθ(3) diamone, and (d) side view of the formed Dnθ(4) diamane.

Full size image

To form the Dnθ(3) diamane, it is necessary to continue the adsorption of hydrogen (or other light adatoms), but on the surface of the lower layer (Fig. 1b). In this case, after some time, all chemically active sp2 С atoms on the formed Donθ(3) diamone should be neutralized by the addition of adatoms brought to the structure. After that, the structure of the Dnθ(3) diamane will be completely formed (Fig. 1c).

The formation of a Dnθ(4) diamane from a four-layer graphene with 0θθ0 stacking (Fig. 2a) can also be carried out according to the Dnθ(3) formation scheme considered above. Here, it is also necessary to start the adsorption process from the surface of the upper layer, when the formation of a semihydrogenated (in the case of H adatoms) moiré diamond-like structure, i.e., a moiré diamone (Donθ) with chemically active sp2 carbon atoms (Fig. 2b) from 0θ bigraphene, is energetically favorable. After some time, such atoms will be covalently bonded to the opposite atoms of graphene, reconstructing it with the formation of the Donθ(3) diamone (Fig. 2c). Moreover, after some time, all chemically active atoms on the formed Donθ(3) diamone will be neutralized by the addition of adatoms brought to the structure. The formation of the Donθ(4) diamone simultaneously with the addition of a flow of atoms from graphene will lead to the reorganization of its surface with the presence of chemically active carbon atoms, on which, in turn, adatoms will be adsorbed. In this way, Dnθ(4) diamane will be formed (Fig. 2d).

Diamanes based on three- and four-layer graphene with a twist angle of θ = 27.8° were selected as models for DFT calculations. Graphene layers at this angle are commensurate and form a periodic structure [22]. Each layer of such graphene contains 28 carbon atoms in the computational cell. The atomic and electronic structures of Dn27.8(3) and Dn27.8(4) multilayer moiré diamanes thus calculated are presented below.

Figure 3 demonstrates the atomic geometries, electronic band structures, and densities of states of selected diamanes.

Fig. 3.
figure 3

(Color online) Side view of (а) Dn27.8(3) and (b) Dn27.8(4) diamanes, (с) the first Brillouin zone of a two-dimensional hexagonal lattice, (d, e) electronic band structures and densities of electronic states for diamanes based on (d) three- and (e) four-layer graphene. The red rectangle shows the calculated cell of the structures. The energy is measured from the top of the valence band.

Full size image

It can be seen that, with an increase in the number of layers from three to four (the number of carbon atoms in a unit cell increases from 78 to 104) in the considered diamanes, the band gap decreases from Eg = 2.41 eV for Dn27.8(3) to Eg = 2.35 eV for Dn27.8(4). These band gaps are narrower than the dielectric gap 3.30 eV in the Dn27.8 moiré diamane [3]. A decrease in the band gap with increasing diamane thickness is also characteristic of untwisted diamanes [23]. The branches of the Dn27.8(3) and Dn27.8(4) band structures, in which the gap is determined, also differ very little from each other. This is apparently due to the possibility of electron tunneling from one C–H surface to another (C'–H') through the “thin” structure of the intermediate АА-bilayer, where the atoms of the two layers are bonded by nearly equal (dC–C = (1.57 ± 0.05) Å) covalent bonds. They are directed along the normal to the quasi-two-dimensional structure of such diamanes and, in this case, are less strained than the C–C bonds between the twisted 0θ and θ0 layers. Dn27.8(3) and Dn27.8(4) diamanes are direct-gap semiconductors with a band gap close to the dielectric gap of 2.12 eV of the AlAs semiconductor, which reveals the possibility of their use in optoelectronic devices [24].

The unit cell of the crystal (Fig. 4a) is similar in atomic structure to the unit cell of the Dn27.8(4) diamane without adsorbed atoms. All С–H bonds are replaced by С–С' bonds with periodic cell patterns. The crystal has an orthorhombic lattice with the parameters \(a = 9.10{\kern 1pt} \) Å and \(c = 8.65{\kern 1pt} \) Å. It is close to the unit cell of the Gr27.8\((\infty )\) artificial moiré graphite, from which it is formed, but has a different crystallographic orthorhombic system because of the increase in the number of nonequivalent atoms with a part of the C atoms “leaving” the planes during the phase transition from Gr27.8\((\infty )\) to the Dn27.8\((\infty )\) crystal in it. Because of the addition of sp3 bonds between periodic patterns, i.e., between layers 1 and 4' and between layers 4 and 1'' (Fig. 4а), the electronic band structure is rearranged: the gap of the indirect-gap optical transition (as in diamond) increases to Eg = 4.02 eV compared to the gap Eg = 2.35 eV in the Dn27.8(4) diamane. This is due to the higher strain of the С–С' bonds, which in the previous cases were less strained С–Н bonds of carbon atoms on the surfaces of Dn27.8(3) and Dn27.8(4) diamanes.

Fig. 4.
figure 4

(Color online) (a) Side view of the atomic structure of the Dn27.8\((\infty )\) crystal, (b) the first Brillouin zone of an orthorhombic crystal lattice, and (с) the band structure and density of electronic states. The red rectangle shows the calculated cell of the structures; the indirect transition is shown by the red arrow. The energy is measured from the top of the valence band.

Full size image

All considered structures are energetically stable. It is known that Dn27.8 has the formation energy Ef = 0.13 eV/atom, comparable to Ef = 0.12 eV/atom for conventional diamond. The formation energy Ef increases with the number of layers M and tends to the energy Ef = 0.37 eV/atom of the Dn27.8(∞) moiré crystal with respect to Ef of graphene.

CONCLUSIONS

To summarize, the density functional theory simulation of the atomic and electronic structures of diamond-like films Dn27.8(M) (M = 3, 4) formed by low-layer graphene with a special selection of stacking of moiré layers 0θθ and 0θθ0, respectively, when complete sp3 hybridization of carbon atoms occurs in them during the chemical adsorption of light atoms (H or F) has been carried out. A hypothetical Dn\(\theta (\infty )\) moiré 3D diamond-like crystal formed by stacks of moiré four-layer graphene is also considered. The presence of two more layers formed by АА-type bigraphene in the unit cell of Gr\(\theta (\infty )\) moiré graphite is the reason for the increase in its band gap in comparison with the Dn\(\theta \)(4) moiré diamane. The same behavior of the branches of the electronic band structures for all the considered structures near the edge of the valence band with a characteristic flattening should be noted (in particular, a narrow miniband below the Fermi level by –0.3eV). The introduction of acceptor impurities or the application of a transverse electric field in diamanes Dn27.8(M) (M = 3, 4) will shift the Fermi level to the narrow miniband region that becomes conducting in this case, which can reveal similar effects observed in bigraphene with a small twist angle [25] in such diamond-like structures. The presence of a large number of narrow peaks in the density of states can lead to the observation of new nonlinear electric and optical, exciton, and photoelectric resonance effects in such moiré diamanes [26–28].

It should be expected that, with the increase in the number of layers, such diamane structures should have higher strength properties than diamanes formed from two twisted layers [4, 6].

The results of this work indicate the possibility of synthesizing multilayer moiré diamane structures with the selected stacking of graphene layers with angles close to 30°.

Note that, from such structures, as well as from ordinary multilayer diamanes, it will be possible to create solid transparent protective coatings for nanodevices and optical elements with properties different from known materials.

The prospects for the use of ordinary diamanes, described in the last review [10], can also be extended to the considered multilayer moiré structures.