Equations of Correlational Magnetodynamics for Ferromagnetic Materials

A new system of equations for correlational magnetodynamics was developed by means of Bogoliubov hierarchy and new approximation for multiparticle distribution functions. The system consists of two equations. One is Landau–Lifshitz–Bloch like equation, and the other describes the evolution of pair correlations. Computational results show that correlational magnetodynamics model match the direct Landau–Lifshitz better than the standard Landau–Lifshitz–Bloch equation.

1. Modern studies of magnetic materials demands models taking into account the temperature fluctuations correctly. These demands are due to the progress in nanotechnologies (since nanostructures prone to thermal effects) and advances in governing processes on short time scales. Apart from applying external field there are different ways to achieve magnetization flip. It may be done with aid of spin-polarized current [1], laser [2] or even temperature variation [3].

Full scaled numerical modelling of nonequilibrium processes in magnetic materials taking into account the temperature is required to create cells of magnetoresistive memory which can be flipped in pulse mode by a composition of heating the recording layer and applying spin-polarized current or magnetic field [4].

Models for magnetic materials come in different scales. On the one hand, spin is a quantum phenomenon on the other in certain cases it is preferable to use models which operate on macroscopic scale. The effect in question may depend upon defects in crystal structure, shape or the sample size. The characteristic time may vary from an attosecond to years. Under such conditions it is impossible to use a single model. For example, Monte-Carlo methods are employed to study equilibrium states [5, 6]. The most widespread class of models is micromagnetic continuous medium based on Landau–Lifshitz–Gilbert equation [7–13]. At the moment the most precise commonly accepted micromagnetic model that takes into account evolution of the average magnetization is the Landau–Lifshitz–Bloch equation (LLB) [14–19].

Deriving a continuous model from discrete one is a hard problem due to intensive and short ranged exchange interaction and temperature fluctuations which should be taken into consideration. This transition appears to be an important fundamental problem by itself. The mean field approximation which is utilized in LLB derivation produces a number of artifacts due to vanished correlation between magnetic moments of closest atoms. Disappearing of exchange energy in the paramagnetic phase and understated relaxation time for a system [20] are the major drawbacks of this approach. It may be a serious restriction on modelling spintronic and magnetic nanoelectronics devices which are working in a pulse mode.

By choosing another approximation for multiparticle distribution functions one can derive the improved LLB equation that takes into account correlations between the nearest particles. In addition this equation is supplemented with another one describing pair correlations (exchange energy) which is similar to equation on total energy density in hydrodynamics.

2. We start from discrete model of magnetic material which is governed by the system of Landau–Lifshitz stochastic equations, which describe evolution of N magnetic moments ${{{\mathbf{m}}}_{i}}(t)$, ${\text{|}}{{{\mathbf{m}}}_{i}}(t){\text{|}} = 1$. Magnetic moments are placed into the nodes of a crystal lattice which have coordinates ${{{\mathbf{r}}}_{i}}$. The system has the form

$$\begin{gathered} \frac{{d{{{\mathbf{m}}}_{i}}}}{{dt}} = - \gamma {\kern 1pt} {\kern 1pt} \text{[}{{{\mathbf{m}}}_{i}} \times {\mathbf{H}}_{i}^{{{\text{eff}}}}] - \alpha \gamma {\kern 1pt} {\kern 1pt} [{{{\mathbf{m}}}_{i}} \times [{{{\mathbf{m}}}_{i}} \times {\mathbf{H}}_{i}^{{{\text{eff}}}}]] \\ + \;\sqrt {2\alpha \gamma T{\kern 1pt} } [{{{\mathbf{m}}}_{i}} \times {{{\boldsymbol{\xi }}}_{i}}(t)]; \\ \end{gathered} $$

(1)

$${\mathbf{H}}_{i}^{{{\text{eff}}}} = - {{\nabla }_{{{{{\mathbf{m}}}_{i}}}}}W = {\mathbf{H}}_{i}^{{{\text{ex}}}} + {\mathbf{H}}_{i}^{{{\text{an}}}} + {\mathbf{H}}_{i}^{{{\text{dip}}}} + {{{\mathbf{H}}}^{{{\text{ext}}}}};$$

$${\mathbf{H}}_{i}^{{{\text{ex}}}} = \sum\limits_j {{J}_{{ij}}}{{{\mathbf{m}}}_{j}};\quad {\mathbf{H}}_{i}^{{{\text{an}}}} = 2K{{{\mathbf{n}}}_{K}}({{{\mathbf{n}}}_{K}} \cdot {{{\mathbf{m}}}_{i}});$$

$${\mathbf{H}}_{i}^{{{\text{dip}}}} = \sum\limits_j \frac{{3({{{\mathbf{m}}}_{j}} \cdot {{{\mathbf{r}}}_{{ij}}}){{{\mathbf{r}}}_{{ij}}} - {{{\mathbf{m}}}_{j}}r_{{ij}}^{2}}}{{r_{{ij}}^{5}}},\quad {{{\mathbf{r}}}_{{ij}}} = {{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}};$$

where γ is the gyromagnetic ratio, α is the damping parameter, H^eff is the effective magnetic field, W is the total energy of the system, and T is the temperature, ${{{\boldsymbol{\xi }}}_{i}}(t)$ are pairwise independent random vectors composed of δ-correlated random variables with the standard normal distribution, ${{\nabla }_{{{\mathbf{m}}i}}}$ is the gradient operator along the magnetic moment ${{{\mathbf{m}}}_{i}}$, H^ex is the exchange field, J_ij is the exchange integral (usually nonzero only for the closest neighbors), H^an is the anisotropy field for the easy axis or the easy plane anisotropy, K is the anisotropy parameter, ${{{\mathbf{n}}}_{K}}$ is the unit vector in the anisotropy direction, and H^dip is the dipole–dipole (magnetostatic) portion of the field. From now on, we use the dimensionless units.

The system of Eqs. (1) allows one to take into account thermal fluctuations, crystal structure defects, and a number of other subtle physical phenomena. However it appears to be too computationally demanding for modelling full-sized devices. In order to overcome this restriction, it is necessary to pass to continuous medium equations. The most sophisticated part of this transition is to factor in the exchange interaction between closest neighbors correctly. We are going to use results of numerical integration (1) as ab initio discrete results. The verification of constructed continuous medium equations is carried out on the basis of these results.

3. Let’s introduce notation

Here, ${{\nabla }_{{ \circ i}}} = {{\nabla }_{{{{{\mathbf{m}}}_{i}}}}} - {{{\mathbf{m}}}_{i}}({{{\mathbf{m}}}_{i}} \cdot {{\nabla }_{{{{{\mathbf{m}}}_{i}}}}}){\text{/}}{\mathbf{m}}_{i}^{2}$ is the tangent to the surface of the sphere part of the gradient, ${{{\mathbf{H}}}_{i}}$ is the effective field, D is the diffusion coefficient in the magnetic moment space, and $f = f(...,{{{\mathbf{m}}}_{i}},...)$ is the distribution function for magnetic moments of a system. Later on, we are going to often use Fokker–Planck-like equations (FPE) [21]

$$\dot {f} = {{\nabla }_{{ \circ i}}}[\gamma {{{\mathbf{m}}}_{i}} \times ({{{\mathbf{H}}}_{i}} + \alpha {\kern 1pt} {\kern 1pt} [{{{\mathbf{m}}}_{i}} \times ({{{\mathbf{H}}}_{i}} - D{{\nabla }_{{ \circ i}}})])f];$$

hence, the notation will significantly abbreviate the expressions.

Let ${{f}^{{(N)}}}({{{\mathbf{m}}}_{1}},...,{{{\mathbf{m}}}_{N}},{\kern 1pt} t)$ be the N-particle distribution function in magnetic moments space. It is possible to rigorously enough derive [22] the N-particle FPE from (1)

(2)

Let’s introduce the single-particle distribution function ${{f}_{i}}$ as

$${{f}_{i}}({{{\mathbf{m}}}_{i}},t) = \int \mathop {\cdots} \limits_{{{S}_{2}}{\ldots} {{S}_{2}}} \int {{f}^{{(N)}}}{\kern 1pt} d{{{\mathbf{m}}}_{{1,...{\kern 1pt} i - 1,{\kern 1pt} i + 1,...{\kern 1pt} N}}}.$$

Here, we denoted integration over a unit sphere by $\int_{{{S}_{2}}} {d{\mathbf{m}}}$. If we integrate (2) with respect to all but one magnetic moments (see the supplementary material), then we will get the system comprised of N single-particle FPE with integral coefficients

(3)

$${\mathbf{H}}_{i}^{{\begin{subarray}{l} (2) \\ {\text{ex}} \end{subarray}} } = \sum\limits_j {{J}_{{ij}}}\int\limits_{{{S}_{2}}} {{{\mathbf{m}}}_{j}}{\kern 1pt} f_{{ij}}^{{(2)}}{\kern 1pt} d{{{\mathbf{m}}}_{j}},$$

(4)

$${\mathbf{H}}_{i}^{{\begin{subarray}{l} (2) \\ {\text{dip}} \end{subarray}} } = \sum\limits_j \int\limits_{{{S}_{2}}} \frac{{3({{{\mathbf{m}}}_{j}} \cdot {{{\mathbf{r}}}_{{ij}}}){{{\mathbf{r}}}_{{ij}}} - {{{\mathbf{m}}}_{j}}r_{{ij}}^{2}}}{{r_{{ij}}^{5}}}{\kern 1pt} f_{{ij}}^{{(2)}}{\kern 1pt} d{{{\mathbf{m}}}_{j}},$$

(5)

where ${{f}^{{(2)}}}$ is the two-particle distribution function.

$$f_{{ij}}^{{(2)}}({{{\mathbf{m}}}_{i}},{{{\mathbf{m}}}_{j}},t) = \int \mathop {\cdots} \limits_{{{S}_{2}}{ \ldots } {{S}_{2}}} \int {{f}^{{(N)}}}{\kern 1pt} d{{{\mathbf{m}}}_{{...{\kern 1pt} i - 1,{\kern 1pt} i + 1,...{\kern 1pt} j - 1,j + 1,...}}}.$$

4. In order to make a complete set of equations one needs to approximate $f_{{ij}}^{{(2)}}$ as a functional of ${{f}_{i}}$ and ${{f}_{j}}$. The standard mean field approximation implies that $f_{{ij}}^{{(2)}} \approx {{f}_{i}}{{f}_{j}}$. In this case, Eq. (3) takes the form

(6)

$$\overline {\mathbf{H}} _{i}^{{{\text{ex}}}} = \sum\limits_j {{J}_{{ij}}}\langle {{{\mathbf{m}}}_{j}}\rangle ,$$

(7)

$$\overline {\mathbf{H}} _{i}^{{{\text{dip}}}} = \sum\limits_j \frac{{3(\langle {{{\mathbf{m}}}_{j}}\rangle \cdot {{{\mathbf{r}}}_{{ij}}}){{{\mathbf{r}}}_{{ij}}} - \langle {{{\mathbf{m}}}_{j}}\rangle r_{{ij}}^{2}}}{{r_{{ij}}^{5}}}.$$

(8)

Let’s assume there is available a smooth (on scales larger than lattice step) six-dimensional distribution function $f({\mathbf{m}},{\mathbf{r}},t)$ which conforms with ${{f}_{i}}({\mathbf{m}},t)$ at the lattice nodes ${{{\mathbf{r}}}_{i}}$. We denote corresponding to it distribution of mean magnetization by $\langle {\mathbf{m}}\rangle ({\mathbf{r}},t)$. In the case ${{J}_{{ij}}} = J$ only for closest neighbors, the exchange field (7) may be approximated with

$$\overline {\mathbf{H}} _{i}^{{{\text{ex}}}} \approx {{a}^{2}}J{{\Delta }_{{\mathbf{r}}}}{{\left. {\langle {\mathbf{m}}\rangle } \right|}_{{{\mathbf{r}} = {{{\mathbf{r}}}_{i}}}}} + {{n}_{b}}J{{\left. {\langle {\mathbf{m}}\rangle } \right|}_{{{\mathbf{r}} = {{{\mathbf{r}}}_{i}}}}},$$

where a is the length of exchange bond, ${{\Delta }_{{\mathbf{r}}}}$ is the Laplace operator in the configuration space, and ${{n}_{b}}$ is the number of nearest neighbors.

The terms in $\overline {\mathbf{H}} _{i}^{{{\text{ex}}}}$ have an apparent physical meaning. The first one with ${{\Delta }_{{\mathbf{r}}}}$ describes the interaction larger than the infinitesimal volume for non-homogeneous spacial distribution $\langle {\mathbf{m}}\rangle ({\mathbf{r}})$. It also brings on spin waves. The second term ${{n}_{b}}J\langle {\mathbf{m}}\rangle$ is responsible for interactions inside the infinitesimal volume. It produces spontaneous magnetization and the ferromagnetic–paramagnetic phase transition. The dipole–dipole interaction field (8) may be written as integral over the volume, linearly depends on $\langle {\mathbf{m}}\rangle$, and has well known methods of calculations [23, 24].

After that (6) takes the form

(9)

$${{{\mathbf{H}}}^{{\text{L}}}} = {{a}^{2}}J{{\Delta }_{{\mathbf{r}}}}\langle {\mathbf{m}}\rangle + {{\overline {\mathbf{H}} }^{{{\text{dip}}}}} + {{{\mathbf{H}}}^{{{\text{ext}}}}},$$

where ${{{\mathbf{H}}}^{{\text{L}}}}$ combine the terms which is responsible for interactions on scales larger than infinitesimal volume.

5. Multiplying Eq. (9) by ${\mathbf{m}}$ and integrating it with respect to $d{\mathbf{m}}$ (see supplementary materials) afterwards, one can obtain LLB equation [14], which describes evolution of $\langle {\mathbf{m}}\rangle ({\mathbf{r}})$:

$$\begin{gathered} \langle \dot {\mathbf{m}}\rangle = - \gamma {\kern 1pt} \text{[}\langle \mathbf{m}\rangle \times {{{\mathbf{H}}}^{{\text{L}}}}] - 2\gamma K(\mathbf{\Phi} + \alpha \mathbf{\Theta} ) \\ - \;\alpha \gamma {\kern 1pt} \widehat \Xi \cdot ({{{\mathbf{H}}}^{{\text{L}}}} + {{n}_{b}}{{\varepsilon }_{G}}J\langle \mathbf{m}\rangle ) - 2\alpha \gamma T\langle \mathbf{m}\rangle , \\ \end{gathered} $$

(10)

$$\mathbf{\Phi} = \langle \mathbf{m} \times {\mathbf{n}_{K}}(\mathbf{m} \cdot {\mathbf{n}_{K}})\rangle ,\quad \widehat \Xi = \langle \mathbf{m} \otimes \mathbf{m} - \widehat I\rangle ,$$

$$\mathbf{\Theta} = \langle \mathbf{m} \times [\mathbf{m} \times {\mathbf{n}_{K}}](\mathbf{m} \cdot {\mathbf{n}_{K}})\rangle ,$$

where $\otimes$ means tensor multiplication, $\widehat I$ is the identity matrix, and ${{\varepsilon }_{G}} \sim 0.8$ is the factor introduced by Garanin in order to take into account mean field fluctuations and get the right critical temperature value [25]. To calculate the integral coefficients $\mathbf{\Phi}$, $\mathbf{\Theta}$, and $\widehat \Xi$, which depend on high-order moments of single-particle distribution function, it is necessary to approximate $f({\mathbf{m}},{\mathbf{r}},t)$, e.g., as¹

$$f \approx \frac{{{{e}^{{{\mathbf{p}} \cdot {\mathbf{m}}}}}}}{{\mathcal{Z}(p)}},\quad \mathcal{Z}(p) = \int\limits_{{{S}_{2}}} {{e}^{{{\mathbf{p}} \cdot {\mathbf{m}}}}}{\kern 1pt} d{\mathbf{m}} = 4\pi \frac{{\sinh p}}{p},$$

(11)

where vector ${\mathbf{p}} = {\mathbf{p}}({\mathbf{r}},t)$ is an approximation parameter, ${\mathbf{p}}\parallel \langle {\mathbf{m}}\rangle$, ${\text{|}}\langle {\mathbf{m}}\rangle {\text{|}} = \coth p - 1{\text{/}}p \equiv \mathcal{L}(p)$, and $\mathcal{L}$ is the Langevin function. The coefficients $\mathbf{\Phi}$, $\mathbf{\Theta}$, and $\widehat \Xi$ may be estimated numerically and fitted analytically (see [26] and supplementary materials). In the equilibrium case, the LLB equation (10) conforms with Curie–Weiss theory with the accuracy of approximation (11).

6. In order to take into account correlations between nearest neighbors, we approximate the two-particle distribution function as

$$f_{{ij}}^{{(2)}} \approx \frac{1}{{Z_{{ij}}^{{(2)}}}}{{[{{f}_{i}}({\mathbf{m}_{i}},t){\kern 1pt} {{f}_{j}}({\mathbf{m}_{j}},t)]}^{\rho }}{{e}^{{\lambda {\mathbf{m}_{i}} \cdot {\mathbf{m}_{j}}}}},$$

(12)

$$Z_{{ij}}^{{(2)}} = \iint\limits_{{{S}_{2}}{{S}_{2}}} {{[{{f}_{i}}({\mathbf{m}_{i}},t){\kern 1pt} {{f}_{j}}({\mathbf{m}_{j}},t)]}^{\rho }}{{e}^{{\lambda {\mathbf{m}_{i}} \cdot {\mathbf{m}_{j}}}}}{\kern 1pt} d{\mathbf{m}_{i}}{\kern 1pt} d{\mathbf{m}_{j}},$$

where the parameter $\lambda \geqslant 0$ describes correlation (i-ndirect included) between closest magnetic moments ${{{\mathbf{m}}}_{i}}$ and ${{{\mathbf{m}}}_{j}}$, the power $\frac{1}{2} \leqslant \rho \leqslant 1$ is required to  comply with the condition ${{f}_{i}} \approx \int_{{{S}_{2}}} {f_{{ij}}^{{(2)}}{\kern 1pt} d{{{\mathbf{m}}}_{j}}}$. The s-implest way to calculate $\rho$ is to solve the equation $\langle \mathbf{m}\rangle =$ $\iint {{S}_{2}}{{S}_{2}}{\mathbf{m}_{i}}f_{{ij}}^{{(2)}}d{\mathbf{m}_{i}}d{\mathbf{m}_{j}}$. Such an approximation may be applied to any two-particle distribution function, but we need only one for the closest particles. Under the condition $\lambda \ll 1$, approximation (12) approaches mean field approximation while $\rho \to 1$. In the opposite extreme case $\lambda \gg 1$ the exponent (12) tends to Dirac delta $\delta ({{{\mathbf{m}}}_{i}} \cdot {{{\mathbf{m}}}_{j}})$ while $\rho \to \frac{1}{2}$. Despite the presence of the power ρ, the dimensionality of the approximation (12) stays the same as for the two-particle distribution function due to ${{Z}^{{(2)}}}$.

The measure of pairwise correlations is defined by

$$\langle \eta \rangle = \langle {{{\mathbf{m}}}_{i}} \cdot {{{\mathbf{m}}}_{j}}\rangle = \iint\limits_{{{S}_{2}}{{S}_{2}}} {{{\mathbf{m}}}_{i}} \cdot {{{\mathbf{m}}}_{j}}{\kern 1pt} f_{{ij}}^{{(2)}}{\kern 1pt} d{{{\mathbf{m}}}_{i}}{\kern 1pt} d{{{\mathbf{m}}}_{j}}.$$

Hence, the exchange energy per particle equals $- {{n}_{b}}J\langle \eta \rangle {\text{/}}2$.

Let’s consider an infinitesimal volume. If the mean magnetization $\langle {\mathbf{m}}\rangle$ is set there are different levels of pairwise correlations $\langle \eta \rangle$ still possible. Each corresponds to distinct configuration of magnetic moments system (Fig. 1). When $\lambda \to \infty$ the pairwise correlations $\langle \eta \rangle \to 1$ (which is the maximum possible value). The other extreme case is the mean field approximation, in which we get $\lambda = 0$ while the pairwise correlations has the lowest possible value $\langle \eta \rangle = {{\langle {\mathbf{m}}\rangle }^{2}}$. The real world system should be somewhere in between those cases. Hypothetically the ferromagnetic material may have $\lambda < 0$ and $\langle \eta \rangle < {{\langle {\mathbf{m}}\rangle }^{2}}$, which corresponds for the most part to the antiparallel orientation of the closest neighbors.

Fig. 1.

Different configurations of the system of magnetic moments with the same mean magnetization in an infinitesimal volume.

7. As mentioned in the preceding part, the mean field approximation works adequately for long-range interactions. Hence, the approximation (12) should be taken into account in estimation of the interaction inside the infinitesimal volume. Therefore (3) takes the form (see supplementary materials)

instead of (9). Note that the exchange field inside the infinitesimal volume becomes antidiffusion with the coefficient ${{n}_{b}}J\Upsilon$ in the magnetic moment space. The spontaneous magnetization is governed by the competition between antidiffusion and diffusion caused by the temperature fluctuations. The same competition is also responsible for the phase transition point position.

In the end applying (12) instead of (10) results in LLB-like equation in the form

$$\begin{gathered} \langle {\mathbf{\dot {m}}}\rangle = - \gamma {\kern 1pt} {\kern 1pt} \text{[}\langle {\mathbf{m}}\rangle \times {{{\mathbf{H}}}^{{\text{L}}}}] - 2\gamma K(\mathbf{\Phi} + \alpha \mathbf{\Theta} ) \\ - \;\alpha \gamma {\kern 1pt} \widehat \Xi \cdot {{{\mathbf{H}}}^{{\text{L}}}} - 2\alpha \gamma (T - {{n}_{b}}J\Upsilon )\langle {\mathbf{m}}\rangle , \\ \end{gathered} $$

(13)

where it is convenient to regard the coefficient $\Upsilon$ as a function of two parameters $\langle m\rangle = {\text{|}}\langle {\mathbf{m}}\rangle {\text{|}}$ and $\langle \eta \rangle$ (Fig. 2).

Fig. 2.

(Color online) Dependence $\Upsilon (\langle m\rangle ,\langle \eta \rangle )$. The example of the equilibrium dependence $\langle \eta \rangle (\langle m\rangle )$ calculated in discrete model is showed with the black line.

In the mean field approximation, Fig. 2 turns into  a curve $\langle \eta \rangle = {{\langle m\rangle }^{2}}$ on which $\Upsilon = \langle m\rangle {\text{/}}p$. The equilibrium condition is $T = {{n}_{b}}J\langle m\rangle {\text{/}}p$; therefore, $\langle m\rangle =$ $\mathcal{L}({{n}_{b}}J\langle m\rangle {\text{/}}T)$. It corresponds to Curie–Weiss theory which yields the critical temperature ${{T}_{{\text{c}}}} = {{n}_{b}}J{\text{/}}3$ greater (Fig. 3) than one obtained from discrete particle modelling (1). In fact, it is due to underrated value $\langle \eta \rangle$ and overvalued function $\Upsilon$. To fix this problem in the mean field approximation, one has to introduce a factor ${{\varepsilon }_{G}} < 1$. At the same time, if we take into account the pairwise correlations and assumes $\langle \eta \rangle \geqslant {{\langle m\rangle }^{2}}$, then the value of the function $\Upsilon$ for a given $\langle m\rangle$ decreases. It leads to a closer match of the discrete modelling results (1).

Fig. 3.

(Color online) Dependence $\langle m\rangle (T{\text{/}}J)$ for the bcc lattice (${{n}_{b}} = 8$) calculated with various models discrete particles (1), LLB with ${{\varepsilon }_{G}} = 0.795$ (2), LLB with ${{\varepsilon }_{G}} = 1$ (3), CMD (4).

In order to track the value of parameter $\langle \eta \rangle$ an addition equation for pairwise correlations is required. Let’s write the second equation of Bogoliubov hierarchy.

$${\mathbf{H}}_{i}^{{(3)}} = 2K({{{\mathbf{n}}}_{K}} \cdot {{{\mathbf{m}}}_{i}}){{{\mathbf{n}}}_{K}} + J{{{\mathbf{m}}}_{j}} + \sum\limits_{k,{\kern 1pt} k \ne j}^N \frac{{{{J}_{{ik}}}}}{{f_{{ij}}^{{(2)}}}}\int\limits_{{{S}_{2}}} {{{\mathbf{m}}}_{k}}f_{{ijk}}^{{(3)}}{\kern 1pt} d{{{\mathbf{m}}}_{k}}.$$

By multiplying it on ${{{\mathbf{m}}}_{i}} \cdot {{{\mathbf{m}}}_{j}}$ and integrating with respect to $d{{{\mathbf{m}}}_{i}}{\kern 1pt} d{{{\mathbf{m}}}_{j}}$, we get (see supplementary materials)

$$\begin{gathered} \frac{{\langle \dot {\eta }\rangle }}{{4\alpha \gamma }} = {{{\mathbf{H}}}^{{\text{L}}}} \cdot \langle \mathbf{m}\rangle \Upsilon - K\Psi \\ - \;\frac{J}{2}\left[ {\langle {{\eta }^{2}}\rangle - 1 + \sum\limits_k {{Q}_{k}}} \right] - T\langle \eta \rangle , \\ \end{gathered} $$

(14)

$$\Psi = \langle {\mathbf{m}_{i}} \cdot [{\mathbf{m}_{j}} \times [{\mathbf{m}_{j}} \times {\mathbf{n}_{K}}]]({\mathbf{m}_{j}} \cdot {{{\mathbf{n}}}_{K}})\rangle ,$$

$${{Q}_{k}} = \langle {\mathbf{m}_{i}} \cdot [{\mathbf{m}_{j}} \times [{\mathbf{m}_{j}} \times {\mathbf{m}_{k}}]]\rangle .$$

Here, the summation is performed over all neighbors of the jth particle except for the ith particle. Equations (13) and (14) combine into the system of correlational magnetodynamics equations (CMD).

8. Three-particle distribution functions $f_{{ijk}}^{{(3)}}$ which depend on the lattice are required to calculate coefficients ${{Q}_{k}}$. We examine ferromagnetic materials with primitive (SC), bcc, and fcc crystal lattices. See Table 1 and Fig. 4.

Table 1. Properties of the crystal lattices in question: ${{n}_{b}}$ is the number of neighbors, ${{n}_{{{\text{f}}.t.}}}$ is the number of distribution functions $f_{{ijk}}^{{(3)}}$, k is the index of the coordination sphere, ${{R}_{k}}$ is the sphere radius measured in units of the lattice step, ${{n}_{{fk}}}$ means the number of distribution function $f_{{ijk}}^{{(3)}}$ that has the third atom in the corresponding kth coordination sphere and, ${{\angle }_{{ijk}}}$ is the angle at the middle particle of the distribution function $f_{{ijk}}^{{(3)}}$

Fig. 4.

Primitive, bcc, and fcc lattices and the types of three-particle distribution functions $f_{{ijk}}^{{(3)}}$. Indices ${{k}_{{1...4}}}$ indicate the coordination sphere which accommodates the third particle.

We are going to use the notation $f_{{k = s}}^{{x{\text{cc}}}}$ for three-particle distribution functional in the xcc lattice, which has the kth particle on the sth coordination sphere.

First of all, we study $f_{{ijk}}^{{(3)}}$ which have all three particles on the line, i.e., $f_{{k = 3}}^{{{\text{sc}}}}$, $f_{{k = 4}}^{{{\text{bcc}}}}$, and $f_{{k = 4}}^{{{\text{fcc}}}}$. If we neglect the indirect correlations between ith and kth particles, we can approximate such functions with $f_{\angle }^{{(3)}} \approx f_{{ij}}^{{(2)}}f_{{jk}}^{{(2)}}{\text{/}}{{f}_{j}}$. That is basically a generalization of mean field approximation for the three-particle distribution functions. The corresponding coefficient ${{Q}_{\angle }}$ (see supplementary materials) looks like

$${{Q}_{\angle }} = \frac{{1 - \rho }}{\rho }\left[ {1 - \frac{2}{\lambda }\langle \eta \rangle - \langle {{\eta }^{2}}\rangle } \right].$$

Another extremal case is the fully symmetric distribution function

$$f_{{k = 1}}^{{{\text{fcc}}}} \equiv f_{\Delta }^{{(3)}} \approx \frac{1}{{{{Z}^{{(3)}}}}}\exp [\sigma {\mathbf{p}} \cdot ({\mathbf{m}_{i}} + {\mathbf{m}_{j}} + {\mathbf{m}_{k}})$$

$$ + \;\varsigma ({\mathbf{m}_{i}} \cdot {\mathbf{m}_{j}} + {\mathbf{m}_{j}} \cdot {\mathbf{m}_{k}} + {\mathbf{m}_{k}} \cdot {\mathbf{m}_{i}})],$$

where σ and $\varsigma$ may be obtained from

$$\iiint\limits_{{{S}_{2}}{{S}_{2}}{{S}_{2}}} {{{\mathbf{m}}}_{i}}f_{\Delta }^{{(3)}}d{{{\mathbf{m}}}_{{i,j,k}}} = \langle {\mathbf{m}}\rangle ,\quad \iiint\limits_{{{S}_{2}}{{S}_{2}}{{S}_{2}}} \eta {\kern 1pt} {\kern 1pt} f_{\Delta }^{{(3)}}{\kern 1pt} d{{{\mathbf{m}}}_{{i,j,k}}} = \langle \eta \rangle .$$

In a similar manner may be estimated by integration of six-particle function for the particles placed at vertices of a regular octahedron (on Fig. 4 octahedron vertices are marked black) if we neglect the indirect correlations between particles in the opposite vertices.

The generalized mean field for $f_{{ijkl}}^{{(4)}}$ yields

For a primitive cubic lattice with $k = 2$ we consider symmetric distribution for particles placed at the vertices of the square

$$f_{{ijkl}}^{{(4)}} \sim \exp [\sigma {\mathbf{p}} \cdot ({\mathbf{m}_{i}} + {\mathbf{m}_{j}} + {\mathbf{m}_{k}} + {\mathbf{m}_{l}})$$

$$ + \;\varsigma ({\mathbf{m}_{i}} \cdot {\mathbf{m}_{j}} + {\mathbf{m}_{j}} \cdot {\mathbf{m}_{k}} + {\mathbf{m}_{k}} \cdot {\mathbf{m}_{l}} + {\mathbf{m}_{l}} \cdot {\mathbf{m}_{i}})$$

$$ + \;\epsilon \varsigma ({\mathbf{m}_{i}} \cdot {\mathbf{m}_{k}} + {\mathbf{m}_{j}} \cdot {\mathbf{m}_{l}})],\quad \epsilon < 1.$$

On its basis it is possible to obtain

$$f_{{k = 2}}^{{{\text{s}}c}} \equiv f_{ \boxtimes }^{{(3)}} = \int\limits_{{{S}_{2}}} f_{{ijkl}}^{{(4)}}{\kern 1pt} d{{{\mathbf{m}}}_{l}},$$

which depends on three independent parameters $\sigma p$, $\varsigma$, and $\epsilon$. There are only two constraints, namely, on $\langle m\rangle$ and $\langle \eta \rangle$. We assume that bonds $\epsilon \varsigma$ in diagonal terms of $f_{{ijkl}}^{{(4)}}$ are caused by indirect correlations and deviate from bonds $\varsigma$ on external edges by the value $J{\text{/}}T$, i.e., $\epsilon = 1 - J{\text{/}}T\varsigma$.

Functions $f_{{k = 2,3}}^{{{\text{b}}cc}}$ present the most challenges. The particles in them are placed at the vertices of the irregular octahedron. That rules out the approach we used to approximate $f_{{k = 2}}^{{{\text{f}}cc}}$. Comparison with discrete modelling results (1) reveals that approximation $f_{{k = 2}}^{{{\text{b}}cc}} + f_{{k = 3}}^{{{\text{b}}cc}} \approx 2f_{ \boxtimes }^{{(3)}}$ produces acceptable results.

As a result (14) takes the form

$$\frac{{\langle \dot {\eta }\rangle }}{{4\alpha \gamma }} = {{{\mathbf{H}}}^{{\text{L}}}} \cdot \langle {\mathbf{m}}\rangle \Upsilon - K\Psi - \frac{J}{2}[\Lambda + \mathcal{Q}] - T\langle \eta \rangle ,$$

(15)

$$\Lambda = \langle {{\eta }^{2}}\rangle - 1 + {{Q}_{\angle }},\quad {{\mathcal{Q}}_{{{\text{s}}c}}} = 4{{Q}_{ \boxtimes }},$$

The integral coefficients Ψ, Λ, ${{Q}_{\Delta }}$, , , just as $\Upsilon$ are functions of $\langle m\rangle$ and $\langle \eta \rangle$. In contrast the coefficient also depends on temperature ${{Q}_{ \boxtimes }} =$ ${{Q}_{ \boxtimes }}(\langle m\rangle ,\langle \eta \rangle ,T)$. All the coefficients were estimated numerically on the cluster computer K60 at KIAM RAS [27]. Analytical fits were found for coefficients $\Upsilon$, Ψ, Λ, and ${{Q}_{\Delta }}$² (see the supplementary material). The rest , , and ${{Q}_{ \boxtimes }}$ are defined on mesh.³ All the coefficients are available as the part of aiwlib library [28].

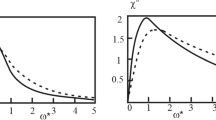
9. The results of the discrete numerical model-ling (1) were compared to modelling of the standard LLB model (10) and the CMD (13) modelling for various values of temperature T, external fields ${{H}^{{{\text{ext}}}}}$, and anisotropy K [27]. A portion of these results are shown of Fig. 5. The discrete particle model in all cases had 64³ lattice cells and periodic boundary conditions. For LLB and CMD we examined the evolution of the magnetization in spatially uniform case.

Fig. 5.

(Color online) Equilibrium magnetization $\langle m\rangle$, exchange energy $\langle W\rangle$, susceptibility χ, and relaxation time τ versus the system temperature T, obtained in the Landau–Lifshitz discrete approach (LL), correlational magnetodynamics approximation (CMD), and mean field approximation (MFA) for systems with SC, bcc, and fcc lattices with no external field or anisotropy H^ext = 0, K = 0.

The initial conditions for discrete particle calculations were set to be uniform magnetization ${{\left. {{{{\mathbf{m}}}_{i}}} \right|}_{{t = 0}}} = {{{\mathbf{m}}}_{{{\text{start}}}}}\forall i$. The method of estimation for the relaxation time may be found in supplementary materials.

For all models the dependences of the equilibrium magnetization and susceptibility are close to each other. In the absence of the external field the CMD approximation slightly shift the critical temperature of the phase transition. According to preliminary review the shift is induced by the approximation error for the single-particle distribution function (11). This suggestion is indirectly supported by the very good match between CMD approximation and discrete modelling results for the case of strong external fields (see supplementary materials, Fig. S3) for functions $\langle m\rangle (T)$ and $\langle W\rangle (T)$. Along with intensifying the external field the approximation error for the single-particle distribution function (11) should decrease due to the growing contribution of the linear terms in approximations.

Exchange energy and relaxation time in CMD approximation matches the results of discrete particle modelling better then mean field approximation. The relatively equal energies means that the two-particle distribution function was chosen appropriately (12). In the mean field approximation, the relaxation time relative error may be as high as 50%. It may negatively affect the quality of modeling devices which work in the pulse mode. On the other hand the relaxation time error in CMD model is triggered by the shifted phase transition point.

10. The CMD model is based on the new approximation of the multi-particle distribution functions. This approximation doesn’t have the rigorous substantiation nonetheless it provides conforms with the original discrete model of the ferromagnetic material with various lattices and in wide value range for the temperature external field and anisotropy.

The CMD mode is a self-consistent theory as it doesn’t use any adjustable parameters. Among other advantages, CMD may explicitly take into account the crystal structure. In contrast to the conventional LLB model CMD employs the extended phase space. In addition to the mean magnetization it considers the pairwise correlations to be independent parameter. By means of that CMD is better suited to describe just as stationary as nonequilibrium processes in the magnetic materials which may improve the quality of the modelling spintronic and magnetic nanoelectronics devices.

The CMD is a new theory (the first publications dates to the end of 2019) and it only starts to establish. It may be father developed with extending it to the antiferromagnetic and ferrimagnetic cases. However the computation of the integral coefficients for these materials is significantly more computationally demanding then form ferromagnetic materials.

It is also worth to take a shot at adding quadratic terms to ${\mathbf{p}} \cdot {\mathbf{m}}$ in the exponent of the approximation for the single-particle distribution function (11). Such correction will result in dramatic sophistication of the CMD system since it will be necessary to supplement with additional equations on the second order moments for the distribution function. From the other point of view it may decrease the incoherence with the discrete modelling results for ferromagnetic materials.