INTRODUCTION

Metallic glasses (MGs) have been of great interest for a long time. On one hand, they have a number of unique physical properties (high yield and tensile strengths, capability of superplastic formation, wear and corrosion resistance, biocompatibility, high-permeability properties, etc.), implying the possibility of applications in some fields from functional materials to environmental protection and medicine. On the other hand, a number of fundamental problems concerning the structure and structural dynamics of MGs, glass transition, relaxation and deformation behavior, etc., have not yet been solved [1–6].

In particular, this refers to the physical nature of excess (i.e., related to a noncrystalline state) thermodynamic potentials (internal energy, entropy, enthalpy, and Gibbs energy) of metallic glasses. Calculations of these potentials began in the 1990s [7, 8] and continue currently [9–12]. The general scheme of these works involves the use of data on the heat capacity in the liquid state and/or below the glass transition temperature Tg together with data on melting heat and entropy to calculate the excess enthalpy, entropy, and Gibbs energy of the supercooled liquid/glassy state with respect to the initial (parentFootnote 1) crystalline state. The results obtained are used primarily to estimate the glass-forming ability of supercooled liquids and kinetics of their crystallization. The physical nature of the formation of the indicated excess thermodynamic potentials has not yet been considered.

The understanding of the excess thermodynamic potentials of solid glass with respect to the parent crystal is of special interest in this field. The solution to this problem would allow one to obtain information on the structural elements of glass, which have, e.g., an increased internal energy and, thereby, significantly affect the macroscopic properties of MGs (e.g., the formation of shear bands and macroscopic plasticity [12]). Meanwhile, to the best of our knowledge, any studies aimed at solving this problem are absent except for recent work [13]. That work is based on interstitialcy theory implying that “defects” of MGs inherited from the melt are similar to interstitial dumbbells in crystalline metals [14–18]. The temperature dependences of the excess enthalpy, entropy, and Gibbs energy with respect to the parent crystalline state were calculated within this approach. It appeared that excess enthalpy values for several MGs coincide within 10–20% with values calculated from calorimetric data and the enthalpy jump at crystallization almost exactly coincides with the heat of crystallization [13]. In this work, we use a similar approach that shows that the excess internal energy of each of ten MGs at room temperature coincides within an accuracy of no less than 10–15% with the elastic energy of the system of interstitial defects frozen-in at the annealing of the melt. It appears that the excess entropy of a glass is proportional to its excess internal energy and the entropy per defect is (20–30)kB (where kB is the Boltzmann constant), which is characteristic of interstitial defects.

IDEA OF THE EXPERIMENT

First, the excess internal energy of MGs with respect to the parent crystal can be calculated from calorimetric data. Heating is accompanied by the release and/or absorption of heat. The integral heat Q at atmospheric pressure within a high accuracy is the change in the internal energy of the glass ΔUQ. This quantity can be determined from differential scanning calorimetry (DSC) data on the differential molar heat flow ΔW = Wgl – Wcr, where Wgl and Wcr are the molar heat flows from the initial glass sample and the sample after complete crystallization occurring at a certain temperature Tcr. The excess internal energy can be calculated by integrating the heat flow over the temperature, and the constant of integration can be determined from the condition that structural defects of glass disappear completely at the temperature of complete crystallization Tcr and the excess internal energy vanishes. Then, the change in the molar internal energy of the MG as a function of the temperature can be represented in the form [13]

$$\Delta {{U}_{Q}}(T) = \frac{1}{{\dot {T}}}\int\limits_T^{{{T}_{{{\text{cr}}}}}} {\Delta W} (T)dT,$$
(1)

where \(\dot {T}\) is the heating rate. The molar excess entropy of the glass with respect to the parent crystal can be determined similarly as [13]

$$\Delta {{S}_{Q}}(T) = \frac{1}{{\dot {T}}}\int\limits_T^{{{T}_{{{\text{cr}}}}}} {\frac{{\Delta W(T)}}{T}} dT.$$
(2)

At the same time, the excess internal energy of the MG is determined according to interstitialcy theory primarily by the elastic energy of the system of interstitial defects frozen upon the annealing of the melt [16, 19]. This energy can be expressed in terms of unrelaxed (high-frequency) shear moduli G and µ of the glass and parent crystal, respectively, through the simple relation [16]

$$\Delta {{U}_{{{\text{el}}}}} = \frac{{{{m}_{\mu }}}}{{\rho \beta }}(\mu - G),$$
(3)

where \({{m}_{\mu }}\) is the molar mass, ρ is the density, and β is the dimensionless shear susceptibility, which determines the diaelastic effect (lowered shear modulus of the glass compared to the shear modulus of the parent crystal) and is a universal integral parameter relating the diaelastic effect, thermal phenomena, anharmonicity of the interatomic interaction potential, and defect structure of the glass [16, 20]. The shear susceptibility for a given MG can be treated as a constant, and the shear susceptibilities of different MGs lie in a quite narrow range \(15 \leqslant \beta \leqslant 23\) [16].

Thus, the excess internal energy can be determined both from DSC data and within interstitialcy theory from shear modulus data. The excess entropy ΔSQ can be calculated from calorimetric data. The results obtained will allow one to make certain conclusions on the nature of ΔUQ and ΔSQ. This fundamental scheme is implemented in this work.

EXPERIMENTAL METHOD

Studies were performed with ten MGs based on Zr, Cu, and Pd (including high-entropy six-component glass) listed in Table 1. Initial MGs were prepared in the form of 2 × 10 × (30–50)-mm plates using the method of vacuum suction of the melt into a copper casting mold and their noncrystallinity was controlled by the X-ray method. The DSC measurements for samples with a mass of about 50 mg were performed on a Hitachi DSC 7020 instrument in a high-purity (99.999%) nitrogen atmosphere. The error of measurement of the heat flow was estimated as ~4%. All measurements were performed at a heating rate of 3 K/min up to the temperature of complete crystallization Tcr. After the measurement of the heat flow Wgl from MGs in the initial state and cooling to room temperature, we measured the heat flow Wcr from the same sample in the crystalline state and then calculated the differential heat flow \(\Delta W\) for further an-alysis.

Table 1. Densities \(\rho \), shear susceptibilities β, differences between the shear moduli of the crystal and glass (µ – G)rt, and excess internal energies \(\Delta U_{Q}^{{{\text{rt}}}}\) and \(\Delta U_{{{\text{el}}}}^{{{\text{rt}}}}\) of the studied MGs calculated by Eqs. (1) and (3) from differential scanning calorimetry and shear modulus data, respectively. Excess \(\Delta S_{Q}^{{{\text{rt}}}}\), calculated by Eq. (2) from differential scanning calorimetry data. All quantities correspond to room temperature
Full size table

The shear moduli G of 5 × 5 × 2-mm samples were measured using the electromagnetic–acoustic transformation method [21, 22] at frequencies of 500–700 kHz in a vacuum of ≈0.01 Pa. The total error of measurement of shear modulus G was estimated as 1–2%, whereas the accuracy of determination of the relative change in the shear modulus was 10–100 ppm depending on the temperature.

RESULTS AND DISCUSSION

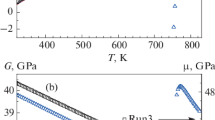
We first discuss the results obtained for the Zr47.5Cu47.5Al5 MG. Figure 1 shows the DSC thermogram of this glass, which has a standard form. The beginning of an endothermic reaction at 675 K corresponds to the glass transition temperature Tg. A further heating results in a large exothermic crystallization peak, which ends at the temperature Tcr ≈ 860 K. These two temperatures are indicated by arrows. This thermogram was then used to calculate the molar excess internal energy ΔUQ by Eq. (1) as a function of the temperature, which is shown in Fig. 2. It is seen that ΔUQ remains approximately constant under heating up to the glass transition temperature Tg, then increases by about 17% up to the temperature of crystallization beginning, and finally decreases to zero at the temperature of complete crystallization Tcr. The excess internal energy at room temperature is \(\Delta U_{Q}^{{{\text{rt}}}} = 5.4\) kJ/mol. Figure 2 also shows the temperature dependence of the excess entropy ΔSQ calculated by Eq. (2). It is seen that the excess entropy repeats within a high accuracy the temperature behavior of the excess internal energy and ΔSQ is approximately proportional to ΔUQ in the entire temperature range under consideration.

Fig. 1.
figure 1

(Color online) Thermogram of differential scanning calorimetry of the Zr47.5Cu47.5Al5 metallic glass. Glass transition and complete crystallization temperatures are indicated.

Full size image
Fig. 2.
figure 2

(Color online) Temperature dependences of the excess internal energy ΔUQ and excess entropy ΔSQ of the Zr47.5Cu47.5Al5 metallic glass calculated by Eqs. (1) and (2), respectively, as well as the elastic energy ΔUel of the system of defects determined by Eq. (3). As seen, the elastic energy ΔUel reproduces well the experimental excess internal energy. Arrows indicate the ΔUQ value at room temperature and calorimetric glass transition temperature Tg.

Full size image

The measured shear modulus data for the same MG are shown in Fig. 3. The shear modulus G of the initial glass decreases smoothly with increasing temperature up to the calorimetric glass transition temperature Tg because of anharmonicity. After that, the decreasing rate of the absolute value |dG/dT| increases significantly up to the temperature of onset of crystallization. Crystallization is accompanied by a stepwise increase in the shear modulus by ≈28%. The shear modulus µ in the crystalline state decreases smoothly with increasing temperature without any singularities.

Fig. 3.
figure 3

(Color online) Temperature dependences of the shear modulus of the Zr47.5Cu47.5Al5 metallic glass in the initial state (\(G(T)\)) and after total crystallization \((\mu (T))\). The calorimetric glass transition temperature Tg and µ–G value at room temperature are indicated.

Full size image

The dashed line in Fig. 2 is the temperature dependence of the elastic energy ΔUel of defects in the same glass calculated by Eq. (3) for the density ρ = 7130 kg/m3 and shear susceptibility β = 17.9 [23]. It is seen that ΔUel(T) very well follows the temperature behavior of the calorimetrically determined excess internal energy ΔUQ. Since the shear susceptibility was calculated from experimental data with an accuracy of about 10–15%, the calculation of ΔUel within interstitialcy theory reproduces the experimental (i.e., calorimetrically determined) excess internal energy ΔUQ of the glass with approximately the same accuracy. This means importantly that the excess internal energy of the glass is determined primarily by the elastic energy of the system of interstitial defects inherited from the melt. After heating to Tcr, defects disappear completely and this energy dissipates into heat, as previously assumed [30].

To what degree is this conclusion generally valid for MGs? To answer this question, we studied other MGs and obtained generally similar results. We emphasize that the elastic energy of the defect subsystem calculated within interstitialcy theory always corresponds well to the calorimetrically determined excess internal energy, differing from the latter by less than 10%. It is convenient to analyze the results using Table 1, which presents the densities ρ, shear susceptibilities β, and differences between shear moduli (µ – G)rt for all studied MGs, as well as the excess internal energies \(\Delta U_{Q}^{{{\text{rt}}}}\) and \(\Delta U_{{{\text{el}}}}^{{{\text{rt}}}}\) calculated by Eqs. (1) and (3) from DSC data and shear modulus data, respectively. Table 1 also presents the excess entropies calculated by Eq. (2). All data are presented for room temperature.

Circles in Fig. 4 are the elastic energies ΔUel of the defect system versus the calorimetrically determined excess internal energy ΔUQ, where digits next to the points correspond to the numbers of the studied MGs according to Table 1. The solid line is the rms approximation of the data with the angular coefficient dΔUel/dΔUQ = 1.03 ± 0.08 and a Pearson coefficient of 0.978. Thus, taking into account the indicated accuracy of determination of the shear susceptibility β in Eq. (3), one can conclude that the experimentally determined excess internal energy of studied MGs coincides within an accuracy of no less than 10–15% with the elastic energy of defect subsystems.

Fig. 4.
figure 4

(Color online) (Circles) Excess internal energy ΔUel of the defect subsystem calculated by Eq. (3) from shear modulus data versus the excess internal energy ΔUQ calculated by Eq. (1) from calorimetric data. Digits mean the compositions of metallic glasses according to Table 1. The solid line is the rms approximation with the angular coefficient KUel = dΔUel/dΔUQ = 1.0. (Triangles) Excess entropy ΔSQ calorimetrically determined by Eq. (2) versus the excess internal energy ΔUQ calorimetrically determined by Eq. (1). The dashed line is the rms approximation of this dependence with the angular coefficient KSQ = dΔSQ/dΔUQ = 1.4 × 10–3 K–1. All data correspond to room temperature. It is seen that ΔUel ≈ ΔUQ and ΔUQ is proportional to ΔSQ.

Full size image

Triangles in Fig. 4 are excess entropies ΔSQ calculated by Eq. (2) versus excess internal energies ΔUQ calculated by Eq. (1)). The dashed line is the rms approximation of the data with the angular coefficient dΔSQ/dΔUQ = (1.4 ± 0.1) × 10–3 K–1 and a Pearson coefficient of 0.974. Thus, the excess entropies of studied MGs increase linearly with their excess internal energies. Since these quantities are unambiguously related to each other, it can be concluded that the excess entropy of MGs is also determined by the elastic energy of their defect subsystems.

It is noteworthy that the excess entropy can be approximately estimated in terms of change in the internal energy by the known thermodynamic formula \(\Delta S \approx \Delta U{\text{/}}T\). For the Zr47.5Cu47.5Al5 MG, under the assumptions that its total stored internal energy \(\Delta U = \Delta U_{Q}^{{{\text{rt}}}}\) = 5.4 kJ/mol (Table 1) and that the this energy is completely released at a temperature of \(T \approx 760\) K when crystallization is mainly completed (see Fig. 1), this formula gives the excess entropy \(\Delta S \approx 7.1\) J/(mol K), which is in good agreement with the calorimetric excess entropy \(\Delta S_{Q}^{{{\text{rt}}}} = 7.3\) J/(mol K) (Table 1).

It seems obvious that the excess internal energy and excess entropy are the most important integral macroscopic parameters of MGs. As seen in Fig. 4, these parameters strongly depend on the chemical composition of the glass (and possibly on conditions of its preparation). Correspondingly, it can be expected that the relaxation of the physical properties of MGs under thermal treatment (e.g., thermal effects upon structural relaxation and crystallization, relaxation of the shear modulus, kinetics of shear viscosity, etc.) will also depend on these quantities. As far as we know, no information on the existence of such dependences has as yet been reported and the search for these dependences can be an intriguing goal of further studies.

According to Eq. (3), the excess internal energy is determined by the molar volume Vµ = mµ/ρ, shear susceptibility β, and the difference between the shear moduli µ and G. It can be expected that the combination of these parameters given by Eq. (3) should be maximal in order to reach the maximum relaxation ability of MGs. According to interstitialcy theory, the shear modulus of the glass decreases with an increase in the concentration c of interstitial defects as G = µexp(–αβc), where α ≈ 1/2 is a dimensionless constant [13, 22] associated with the elastic field of the defect [16]. Then, the difference µ – G in Eq. (3) is µ ‒ G ≈ µαβc, i.e., is proportional to the concentration of defects. Thus, the maximum excess internal energy that should expectedly lead to the maximum relaxation ability of the glass increases with the concentration of defects (which is reasonable) and with Vµ.

The entropy per defect can be estimated as Sd = ΔSQ/(cNAkB), where NA is the Avogadro number. Accepting c = 0.03 for the typical concentration calculated within interstitialcy theory from data on the relaxation of the shear modulus [16] and the average value ΔSQ ≈ 5.5 J/(mol K) in Table 1 for the molar entropy of the glass, we obtain the estimate Sd ≈ 20 for the total entropy per defect (including the vibrational and configurational components). A high value Sd = 10–20 is characteristic of interstitial dumbbells in crystals and is approximately an order of magnitude higher than the respective value for vacancies [31]. Estimates of the entropy per defect for MGs are Sd = 20–30 [13, 16]. Thus, excess entropies presented in Table 1 certainly indicate that relaxation changes in MGs determining the structural relaxation and crystallization with accompanying changes in the physical properties should be controlled by interstitial dumbbell defects. Furthermore, since an estimate of about 0.01 for the concentration of defects is usually accepted in other model approaches (see, e.g., [32]) and the excess entropy is calculated by Eq. (2) with experimental data, the excess entropies ΔSQ presented in Table 1 can confirm the mechanism of relaxation of MGs caused by interstitial defects irrespective of the model approach used for the analysis.

To conclude, we emphasize that the parent crystal is considered in interstitialcy theory as the ground energy state, whereas glass is interpreted as a crystal containing several percent of interstitial dumbbells. Correspondingly, the excess internal energy of the glass given by Eq. (3) is a certain addition to the internal energy of the crystal. This was implied already in the first work by Granato [14] devoted to interstitialcy theory and was later formulated in an explicit form (see, e.g., [33]). Numerous tests of Eq. (3) for various experimental situations always confirmed its validity with a high accuracy (about 10–15% or better) (see, e.g., review [16] and work [13]). This work also confirms this conclusion. Consequently, this relation between the internal energies of glass and crystal can be interpreted as an established experimental fact. At the same time, any structural relation between glass and crystal is not implied in interstitialcy theory.

CONCLUSIONS

The excess internal energies ΔUQ and excess entropies ΔSQ of ten metallic glasses with respect to their parent crystalline states have been determined from calorimetric studies. It has been shown that ΔSQ increases linearly with ΔUQ. The elastic energy ΔUel of the subsystem of interstitial defects assumingly responsible for the structural relaxation and crystallization of metallic glasses has been calculated within interstitialcy theory using high-frequency shear modulus data. It has been established that the quantities ΔUQ and ΔUel coincide with each other within an accuracy of no less than 10–15%. It has been concluded that the excess internal energy and excess entropy of metallic glasses are due primarily to the elastic energy of interstitial defects frozen-in at the annealing of the melt. The dissipation of this energy into heat under heating reduces ΔUQ and ΔSQ to zero at the temperature of complete crystallization. It has been hypothesized that the relaxation of the structure of metallic glasses increases with the excess internal energy ΔUQ, which in turn increases with the concentration of interstitial defects and the molar volume.

The entropy per defect Sd estimated from the calculated excess entropy ΔSQ is Sd ≈ (20–30)kB, which is characteristic of interstitial dumbbells in crystals and of defects in metallic glasses. This estimate is in essence based on experimental data; consequently, it is independent of model concepts used for analysis.