The collective properties of electrons and holes in semiconductors and the possibility of their Bose–Einstein condensation have attracted considerable attention for a long time since the pioneering works by L.V. Keldysh et al. in the mid-1960s [1, 2]. Electrons and holes in semiconductors, individually being fermions, can form bound states that, under certain conditions, have the properties of Bose–Einstein statistics. In the low density case, these bound states are excitons, and in high-density modes, an ensemble of collectively paired electrons and holes resembles a system of Cooper pairs in a superconductor, and it is often called the e–h BCS-like state. When an electron–hole ensemble is placed in a single-mode optical microresonator, exciton states bound with photons of the resonant field—polaritons—can appear. Bose–Einstein condensation of excitons and exciton-polaritons has been observed at low temperatures in some semiconductors, e.g., in Cu2O and GaAs/AlGaAs quantum-well structures [3–6].

The Bose–Einstein dynamics of exciton condensation upon interaction with photons was theoretically studied in [7–9]. A theoretical model based on rate equations demonstrated the possibility of spontaneous condensation of excitons formed using resonant pumping by a laser field at cryogenic temperatures. It was found that the dephasing kinetics and loss of coherence of the condensate strongly depends on its density. In addition, the dephasing time, and, consequently, the condensate lifetime increase in proportion to the square of its density. Hence, the destruction of coherence during collisions within the ensemble does not occur, although the collision frequency increases with the condensate density [8].

The emergence of a nonequilibrium BCS-like electron–hole state in semiconductor heterostructures at room temperature during a superradiant phase transition was experimentally discovered in our previous works [10–13]. It turned out that the experimental results are well explained by the statistical properties of the quasiparticles obtained by the Bogoliubov transformation rather than by the standard properties of electrons and holes that are not coupled to each other. The conditions and mechanism for the emergence of such an unusual electron–hole state with a long-range order [14] at room temperature were qualitatively described in our previous work [12]. The two decisive factors are the high density of electrons and holes (strong degeneracy of the semiconductor) and the presence of resonant photons of the field in the exciton part of the spectrum, which are mediators in the formation of a coherent state. The recombination of the nonequilibrium BCS-like state is observed in the form of high-power femtosecond superradiant pulses. In addition, the coherence of superradiance exceeds the coherence of laser radiation observed in the same samples, and the pulse propagation in the medium has a superluminal nature [14, 15].

We tried to explain these experimental data in [16], where the fundamental possibility of condensation of electron–hole pairs in a highly degenerate semiconductor at room temperature was shown. However, the dynamics of this process has not been studied. In this work, the simplest model that allows one to qualitatively understand the mechanism of formation of a quasi-stable bosonic state in a strongly degenerate electron–hole system is developed for the first time. In addition to the previously published results, it is explicitly demonstrated that a superradiant state is not formed in the absence of photons of a resonant electromagnetic field at any arbitrarily large electron and hole densities.

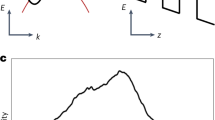
The band diagram in our case is illustrated schematically in Fig. 1. The case of intrinsic GaAs under strong current pumping, which corresponds to the experimental situation in the cited works, is considered. There is a strongly degenerate ensemble of electrons and holes. In this case, the quantum degeneracy criterion is satisfied when the thermal de Broglie length exceeds the average distance between electrons and holes [17]. The diagram in Fig. 1 is for illustrative purposes only, to show the presence of a system of free electrons and holes in the bands and a system of bound pairs (bosons) and their mutual arrangement on the energy scale. Within the scope of our simplified model, we do not consider specific dependences of the energy on the wave vector. For our mechanism of the bosonic state stability, the presence of a filled conduction band above the bosonic level, which is in the exciton part of the spectrum, is important. The fermion ensemble inside the bands and the ensemble of bound electrons and holes in the exciton part of the spectrum will be considered simultaneously. The conversion of fermions into bosons occurs owing to field photons, as previously assumed [12, 16]. To develop a numerical model, the conduction and valence bands are divided into a series of equidistant energy levels \(\{ {{E}_{i}}\} \).

Fig. 1.
figure 1

Schematic representation of the band structure.

Full size image

The zero level \({{E}_{0}}\) corresponds to the bottom of the conduction band. Electrons and holes at this energy level will interact with field photons and form bound pairs (bosons) in accordance with the model proposed earlier [10, 12]. The intraband dynamics of charge carriers is well studied [18–20]. The dynamics of the distribution of electrons\({{f}_{e}}({{E}_{i}})\) and holes \({{f}_{h}}({{E}_{i}})\) at the levels \(\{ {{E}_{i}}\} \), \(i > 0\), is described by the Boltzmann equation [18, 20]

$$\frac{{d{{f}_{e}}({{E}_{{ei}}})}}{{dt}} = \sum\limits_{ej} \Gamma _{{{\text{in}}}}^{e}({{E}_{{ei}}},{{E}_{{ej}}}){{f}_{e}}({{E}_{{ej}}})(1 - {{f}_{e}}({{E}_{{ei}}}))$$
$$ - \;\sum\limits_{ej} \Gamma _{{{\text{out}}}}^{e}({{E}_{{ei}}},{{E}_{{ej}}}){{f}_{e}}({{E}_{{ei}}})(1 - {{f}_{e}}({{E}_{{ej}}}))$$
(1)
$$ - \;\frac{{{{f}_{e}}({{E}_{{ei}}}) - {{F}_{e}}({{\mu }_{e}},{{T}_{{eh}}})}}{{{{\tau }_{{cc}}}}},$$
$$\frac{{d{{f}_{h}}({{E}_{{hi}}})}}{{dt}} = \sum\limits_{hj} \Gamma _{{{\text{in}}}}^{h}({{E}_{{hi}}},{{E}_{{hj}}}){{f}_{h}}({{E}_{{hj}}})(1 - {{f}_{h}}({{E}_{{hi}}}))$$
$$ - \;\sum\limits_{hj} \Gamma _{{{\text{out}}}}^{h}({{E}_{{hi}}},{{E}_{{hj}}}){{f}_{h}}({{E}_{{hi}}})(1 - {{f}_{h}}({{E}_{{hj}}}))$$
(2)
$$ - \;\frac{{{{f}_{h}}({{E}_{{hi}}}) - {{F}_{h}}({{\mu }_{h}},{{T}_{{eh}}})}}{{{{\tau }_{{cc}}}}},$$

where \({{F}_{{e,h}}}\) is the Fermi distribution with the energy \(E_{{e,h}}^{{\text{F}}}\) and temperature \({{T}_{{eh}}}\), and \(\Gamma _{{{\text{in}}}}^{e}\), \(\Gamma _{{{\text{in}}}}^{h}\), \(\Gamma _{{{\text{out}}}}^{e}\), and \(\Gamma _{{{\text{out}}}}^{h}\) are the scattering rates determined by interactions with phonons according to [18, 20]. Since the characteristic charge carrier collision time \({{\tau }_{{{\text{cc}}}}}\) in GaAs at room temperature is about 50 fs, the distribution functions within the bands almost instantly become Fermi functions. The Fermi energies of electrons and holes, measured from the bottom of the bands, depend on the carrier density and are determined by the formulas

$${{n}_{0}} = {{N}_{e}}{{F}_{{1/2}}}({{\eta }_{e}}),\quad {{N}_{e}} = 2{{\left[ {\frac{{2\pi m_{e}^{*}kT}}{{{{h}^{2}}}}} \right]}^{{3/2}}},$$
$${{n}_{0}} = {{N}_{{hh}}}{{F}_{{1/2}}}({{\eta }_{h}}) + {{N}_{{lh}}}{{F}_{{1/2}}}({{\eta }_{h}}),$$
$${{N}_{{hj}}} = 2{{\left[ {\frac{{2\pi m_{{hj}}^{*}kT}}{{{{h}^{2}}}}} \right]}^{{3/2}}},$$

where \({{\eta }_{c}} = E_{c}^{{\text{F}}}{\text{/}}k{{T}_{c}}\), \(c = e\), h, \({{n}_{0}}\) is the carrier density, \({{F}_{{1/2}}}\) is the half-order Fermi integral, and index j corresponds to heavy and light holes. The rate equations for the distribution function \({{f}_{0}}\) of the lowest level \(i = 0\) and for the number of bosons \({{n}_{x}}\) and the number of field photons \({{n}_{p}}\) can be written as [21–23]

$$\frac{{d{{f}_{0}}}}{{dt}} = - \frac{{{{f}_{0}} - F_{e}^{0}}}{{{{\tau }_{{{\text{cc}}}}}}} + C(1 - {{f}_{0}}){{n}_{x}} - K{{f}_{0}}{{n}_{p}},$$
(3)
$$\frac{{d{{n}_{x}}}}{{dt}} = - \frac{{{{n}_{x}}}}{{{{\tau }_{{sp}}}}} + {{K}_{0}}{{f}_{0}}{{n}_{p}} - \sum\limits_j {{\Gamma }_{j}}{{n}_{x}},$$
(4)
$$\frac{{d{{n}_{p}}}}{{dt}} = - \frac{{{{n}_{p}}}}{{{{\tau }_{{{\text{ph}}}}}}} + {{K}_{1}}{{n}_{x}}{{n}_{p}}.$$
(5)

Equation (3) describes the establishment of the Fermi distribution function at the zero energy level due to fast collisions, an increase in the number of electrons at this level due to the decay of bosons, and their decrease due to stimulated boson generation by resonant photons. Equation (4) describes the process of spontaneous boson recombination, stimulated generation of bosons by field photons, and collision-induced decay of bosons into an electron and a hole. The latter process strongly depends on the degree of degeneracy of the semiconductor or, in other words, on the Fermi energy of electrons and holes. This mechanism is described in detail in [12, 24]. Since the decay of a boson requires the presence of free levels for the electron and hole simultaneously, the absence of a free level for at least one particle makes the boson decay impossible. In our case of a sufficiently strong degeneracy of electrons, bosons decay by colliding with each other and with free electrons and holes, and during interaction with acoustic and optical phonons. It is quite difficult to accurately calculate the dynamics of all these processes. This simplified model involves the simple assumption that the total boson decay rate \(\sum\nolimits_j {{\Gamma }_{j}}\) in Eq. (4) is proportional to the number of free levels in the conduction band. The number of free levels decreases significantly with increasing \(E_{e}^{{\text{F}}}\) and tends to zero when all levels are occupied [12]. In other words, the boson decay rate \(\sum\nolimits_j {{\Gamma }_{j}}\) should depend on the degree of degeneracy (carrier density). The maximum energy that an electron can receive during the boson decay is the energy of an optical phonon, which is \(\hbar \Omega \) = 36 meV in GaAs. For this reason, we assume that the decay rate is proportional to the number of free levels in the range \(\hbar \Omega \) above the bottom of the conduction band, or

$$\sum\limits_j {{\Gamma }_{j}} = 3\left[ {\frac{2}{3}{{{(\hbar \Omega )}}^{{3/2}}} - \int\limits_0^{\hbar \Omega } \frac{{\sqrt y dy}}{{1 + \exp (y - E_{e}^{{\text{F}}})}}} \right].$$

Equation (5) describes the dynamics of field photons, where the first term describes the decrease in the number of photons due to scattering, radiation to the environment, etc., with the lifetime \({{\tau }_{{{\text{ph}}}}}\), and the second term describes the stimulated generation of photons due to the decay of bosons. The coefficients K, \({{K}_{0}}\), and \({{K}_{1}}\) are proportional to the optical gain in GaAs.

Equations (1)–(5) were numerically solved for different initial carrier densities \({{n}_{0}}\), which varied over a wide range from 5 × 1017 to 7 × 1018 cm–3. This range covers typical lasing values ((1–2) × 1018 cm–3) and characteristic values of densities for a superradiant phase transition, measured experimentally ((5–6) × 1018 cm–3) [10, 13, 24]. The calculation results are demonstrated in Figs. 2–5. Figures 2 and 3 show the calculated dependences of the density of bosons \({{n}_{x}}\) and photons \({{n}_{p}}\) on the electron Fermi energy divided by kT. The lasing mode in GaAs heterostructures corresponds to a dimensionless Fermi energy of no more than 2, while in the superradiant mode this value exceeds 5. The boson density increases exponentially with the Fermi energy. Figure 3 demonstrates that the intensity of the recombination radiation of bosons increases sharply at a certain Fermi energy. This point corresponds to the beginning of the superradiant transition in the system.

Fig. 2.
figure 2

(Color online) Boson density versus the normalized Fermi energy of electrons. The red line corresponds to the dependence \(\exp (E_{e}^{{\text{F}}})\).

Full size image
Fig. 3.
figure 3

(Color online) Density of photons from recombination of bosons versus the normalized Fermi energy of electrons. The critical Fermi energy \({{\mu }_{{{\text{cr}}}}} \approx 5.8\) corresponds to a sharp increase in the radiation intensity.

Full size image
Fig. 4.
figure 4

(Color online) Normalized critical Fermi energy versus the photon lifetime for optical gains of (green line) 2.0 × 10–16, (blue line) 3.0 × 10–16, and (red line) 4.0 × 10–16 cm–2.

Full size image
Fig. 5.
figure 5

(Color online) Normalized critical Fermi energy versus the optical gain at photon lifetimes of (blue line) 1.0, (green line) 2.0, and (red line) 3.3 ps.

Full size image

This behavior of the boson number and the photon density can be explained as follows. At carrier densities of n0 ~ (0.1–2) × 1018 cm–3 (spontaneous and laser radiation), the degeneracy of the conduction band is not strong enough (Fermi energy \(E_{e}^{{\text{F}}} < 5\)). The energy range ~\(\hbar \Omega \) in the conduction band includes a sufficient number of free levels, which are occupied by electrons during the ultrafast destruction of bosons. Therefore, the number of bosons is vanishingly small since the temperature of the medium is 300 K. However, as the density increases to n0 ~ (5–6) × 1018 cm–3, the degeneracy of the band is so strong that all levels in the considered energy range become occupied by electrons. In this case, the rate of boson destruction drops sharply since there is no free level for the transition of an electron from the bound pair (bottom is the band gap and top is the band completely filled with electrons). The number of bosons and the intensity of radiation increase sharply (superradiant transition occurs). This process was qualitatively described in [12, 24].

Calculations showed that the critical Fermi energy \({{\mu }_{{{\text{cr}}}}}\) depends on the optical gain of the semiconductor, i.e., on the multiplication rate of photons (and, consequently, of bosons) in the medium, and on the photon lifetime \({{\tau }_{{{\text{ph}}}}}\), i.e., on the photon loss value. The last parameter is determined by the sample length L, the reflection coefficient of the facet of the sample R, internal losses \({{\alpha }_{i}}\), and the group velocity of light in the medium vg

$${{\tau }_{{{\text{ph}}}}} = {{\left[ {{{v}_{{\text{g}}}}({{\alpha }_{i}} + \frac{1}{{2L}}\ln \frac{1}{R}} \right]}^{{ - 1}}}.$$

For typical values of \(L = 100{-} 500\) μm, R = 0.30–0.35, and \({{a}_{i}} = 10{-} 20\) cm–1, the lifetime of a photon in real structures lies in the range of 1–10 ps.

Figure 4 demonstrates the calculated dependences of the critical Fermi energy on \({{\tau }_{{{\text{ph}}}}}\) for three values of the optical gain. Obviously, in the absence of resonant photons, the superradiant phase transition cannot be achieved at any electron–hole densities. In experiments [10–15], \({{\tau }_{{{\text{ph}}}}}\) = 2–3 ps, and the superradiance was observed at densities of (5–6) × 1018 cm–3, which is in good agreement with the calculated values of \({{\mu }_{e}}\) in Fig. 4.

Figure 5 demonstrates the calculated dependences of the critical Fermi energy on the optical gain for three values of \({{\tau }_{{{\text{ph}}}}}\). According to our model and similar to Fig. 4, in the absence of optical gain in the medium, the superradiant phase transition does not occur (\({{\mu }_{{{\text{cr}}}}} \to \infty \)). Typical values of the effective optical gain coefficient in bulk GaAs are in the range of (2–3) × 10–16 cm–2 [25]. The calculated critical \({{\mu }_{e}}\) values range from 5 to 7, which is in good agreement with the experimental data.

To summarize, the simplest model that allows one to qualitatively understand the formation mechanism of a quasi-stable bosonic state in a strongly degenerate electron–hole system has been constructed for the first time. The presented theoretical model confirms and extends the previously stated hypothesis about the conditions and mechanism for a superradiant phase transition in a semiconductor at room temperature [10–13]. Two conditions are necessary for this phase transition. First, the density of electron–hole pairs and, accordingly, the degeneracy of the conduction band must be so high that electrons occupy all levels in an energy range equal to the optical phonon energy. In bulk intrinsic GaAs, this corresponds to densities of (5–6) × 1018 cm–3 and higher. Second, the sample must contain a resonant electromagnetic field with a photon energy close to the band gap. It has been explicitly demonstrated that the superradiant state is not formed at any arbitrarily large electron and hole densities in the absence of resonant electromagnetic field photons. In experiments [10–15] with GaAs/AlGaAs heterostructures, the geometry of samples consisting of three sections in one resonator was chosen so that this optical field appears because of the free recombination of electrons and holes located near the band gap. An alternative method may be the application of an external field from a tunable laser source. The constructed simplified numerical model based on the rate equations describes well our previous experimental data.