INTRODUCTION

Technical progress in the miniaturization of solid-state electronics devices currently makes it possible to prepare ultrathin dielectric films in tunneling junctions with a thickness of about one unit cell of a crystal [1–5]. Although two-dimensional structures can have unique features compared to their bulk analogs [6, 7], band calculations of the electronic structure of bulk crystals are performed in most of the studies of the electronic properties of thin dielectric films [3, 5, 8, 9]. In particular, the authors of [9] showed that the width of the band gap EG of silicon dioxide depends on the length of the Si–O bond and the angle between the Si–O–Si bond, but the number of bonds was disregarded. Calculated EG values are in agreement with its experimental values [10–12]. Thus, the dependence of the parameters of the electronic structure of oxides forming a dielectric layer on the dimension of the crystal has not yet been studied. Since silicon oxide is a key insulator in silicon devices [1–5, 13], the aim of this work is to calculate nonempirically the electronic structure of the two-dimensional silicon dioxide crystal with a thickness of about one unit cell and to study the dependence of the electronic properties of the nanocrystal on its composition and thickness of the ultrathin layer.

CALCULATION METHOD

The electronic structure of the two-dimensional crystal was calculated within the density functional theory using the Vienna ab initio simulation package (VASP) based on the projection augmented wave (PAW) method [14]. The generalized gradient approximation (GGA) in the Perdew–Burke–Ernzenhof form [15] was used for the exchange correlation potential and the standard VASP pseudopotentials were used. The number of divisions in the integration over the irreducible part of the Brillouin zone was 20, which corresponds to the 6 × 6 × 1 set of k-points, and the maximum wave vector used in the set of plane waves corresponds to an energy of 250 eV. Self-consistent calculations gave the optimized positions of all atoms and the total energy of the system, and the band structure of the compound, the electron density of states, etc., were then calculated. The process of optimization was performed under the requirement that forces acting on atoms were weaker than 0.1 eV/Å. In the calculations, the distance between nanocrystal layers in the direction of the c axis (no less than 1.2 nm) was chosen such that the interaction between them can be neglected. Nanocrystal layers in the a and b directions are considered as infinite.

The results were refined in the in the GW approximation [16], where the self-energy operator is represented as the product of the Green’s function G of the system of interacting electrons and the screened potential W produced by quasiparticles. It is well known that the density functional calculations underestimate (by a factor of 1.5–2) the band gap for all materials. The subsequent application of the GW quasiparticle approximation provides realistic values of the band gap close to experimental values.

RESULTS AND DISCUSSION

Our calculations of the electronic structure of bulk silicon dioxide give the following widths of the band gap: \({{E}_{{\text{G}}}} = 7.97\)eV for the hexagonal unit cell (β‑quartz), EG = 7.79 eV for the trigonal unit cell (α‑quartz), EG = 9.35 eV for the cubic unit cell (А‑cristobalite), EG = 7.91 eV for the tetragonal unit cell (α‑cristobalite), and EG = 8.23 eV for the tetragonal unit cell (stishovite). The experimental width of the band gap of SiO2 is EG = 9.0 eV with the allowed shift \(\Delta = \pm 3.2\) eV [10–12].

Ab initio calculations were performed for the trigonal unit cell (\(\alpha \)-quartz) of two-dimensional silicon dioxide.

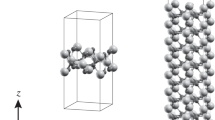
Figure 1 shows (а) the 2 × 2 × 1 cell (the unit cell is indicated by lines) of the bulk α-quartz crystal and (b, с) the same 2 × 2 × 1 cell of the two-dimensional nanocrystal (film) consisting of nine atomic layers. Atoms lying at the same height in the c axis form a “layer” as in the bulk crystal. Two close-lying layers of oxygen atoms are located between silicon layers.

Fig. 1.
figure 1

(Color online) Structure of α-quartz compounds: (a) bulk crystal, (b) two-dimensional nanocrystal with nine atomic layers, and (c) its two-dimensional projection. Large and small circles are Si and O atoms, respectively.

Full size image

The results of nonempirical calculations of ultrathin SiO2 nanocrystals are summarized in Table 1.

Table 1. Structural and electronic characteristics of the two-dimensional α-quartz nanocrystal
Full size table

For n Si atoms, there are three sets of O atoms: \(2n - 2\), \(2n - 1\), and \(2n\). Depending on the number of O layers in the nanocrystal, three different behaviors of the band gap EG are possible. The first behavior occurs at four O layers \((n = 3)\): the band gap is EG = 6.84 eV and increases with n to EG = 7.87 eV, which is close to the band gap in the bulk crystal. The second behavior takes place at five O layers \((n = 3)\): the band gap is EG = 7.16 eV and varies slightly with n, reaching EG = 7.25 eV at n = 17, 19. The third behavior occurs at six O layers \((n = 3)\): the band gap is absent and becomes either small (maximum of 1.22 eV) or zero with increasing n.

Figure 2 shows the total electron density of states of two-dimensional silicon dioxide in all three cases for the numbers of layers 8, 9, and 10 and the thickness of the crystal d from 0.42 to 0.52 nm, respectively. All three plots are similar and include, first, the band of primarily O p states, then a band gap of several electronvolts, and finally the band of primarily Si p states. Only the position of the Fermi level indicates whether the nanocrystal is insulator, semicondutor, or metal. The Fermi level is in turn determined by the ratio of the numbers of Si and O atoms and by the fraction of atoms located on the surface of the nanofilm.

Fig. 2.
figure 2

Total electron density of states of the SiO2 two-dimensional nanocrystal with (a) eight, (b) nine, and (c) ten atomic layers.

Full size image

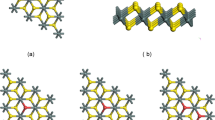
The structure of trigonal silicon dioxide in the infinite crystal is described by the Mott octahedral rule [5], according to which each silicon atom is coordinated with four oxygen atoms and each oxygen atom is coordinated with two silicon atoms. The simple Mott rule is not satisfied in the two-dimensional nanocrystal because Si atoms have from two to four neareset neighbors, whereas O atoms have one or two nearest neighbors. The average number of nearest bonds between Si and O atoms in the two-dimensional nanocrystal is described by empirical formulas (Table 2).

Table 2. Number of the nearest neighbors of Si and O in two-dimensional silicon dioxide
Full size table

The dependence of the band gap on the number of atomic layers is due to different numbers of O atoms on the surface of the two-dimensional nanocrystal: (a) in the absence of O atoms on the surface, the number of atomic layers can be 7, 10, 13, etc.; (b) in the presence of one O atom on the surface, the number of atomic layers can be 8, 11, 14, etc.; and (c) in the presence of two O atoms on the surface, the number of atomic layers can be 9, 12, 15, etc. Each oxygen atom in the bulk SiO2 crystal has two Si nearest neighbors. The bond between them is ion covalent. The O atom on the surface of the nanocrystal is bonded only to one Si neighbor. Unpaired p electrons of two surface O atoms (case (b), nine layers) primarily form the band passing through EF (Figs. 2b and 3, where the partial electron density of states in oxygen for this case is shown).

Fig. 3.
figure 3

(Color online) Partial electron density of states of oxygen in SiO2 with nine atomic layers.

Full size image

CONCLUSIONS

The analysis of the reported calculations has shown that the parameters of the electronic structure of SiO2 qualitatively depends on the ratio of the number of silicon and oxygen atoms in the unit cell of the two-dimensional crystal. It has also been shown that the violation of the Mott rule occurring at a certain ratio of the number of silicon and oxygen atoms qualitatively changes the electronic properties of the two-dimensional silicon dioxide crystal and, namely, shifts the Fermi level to the valence band. The significant change in the electronic properties of the ultrathin silicon dioxide film should be taken into account when forming the ultrathin dielectric layer in silicon tunneling heterostructures. The performed calculations are of very important applied significance for silicon tunneling diodes and transistors where the two-dimensional silicon dioxide crystal is used as an undergate dielectric layer in the multilayer structure with “high‑K” insulators [1, 3, 13, 17].