Fermi–Pasta–Ulam recurrence and modulation instability

Abstract

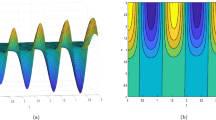
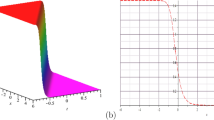
We give a qualitative conceptual explanation of the Fermi–Pasta–Ulam (FPU) like recurrence in the onedimensional focusing nonlinear Schrodinger equation (NLSE). The recurrence can be considered as a result of the nonlinear development of the modulation instability. All known exact localized solitary wave solutions describing propagation on the background of the modulationally unstable condensate show the recurrence to the condensate state after its interaction with solitons. The condensate state locally recovers its original form with the same amplitude but a different phase after soliton leave its initial region. Based on the integrability of the NLSE, we demonstrate that the FPU recurrence takes place not only for condensate, but also for a more general solution in the form of the cnoidal wave. This solution is periodic in space and can be represented as a solitonic lattice. That lattice reduces to isolated soliton solution in the limit of large distance between solitons. The lattice transforms into the condensate in the opposite limit of dense soliton packing. The cnoidal wave is also modulationally unstable due to soliton overlapping. The recurrence happens at the nonlinear stage of the modulation instability. Due to generic nature of the underlying mathematical model, the proposed concept can be applied across disciplines and nonlinear systems, ranging from optical communications to hydrodynamics.