Geomagnetic Field Disturbance by an Acoustic-Gravity Wave Generated by Ionizing Radiation of Solar Flares

Abstract

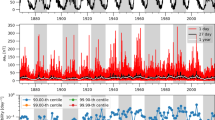
A model of generating the geomagnetic field oscillations with periods of 5–10 min by an acoustic-gravity wave, which are observed during the impact of solar flare ionizing radiation on the ionosphere, is considered. The magnetograms at different distances from the subsolar point on the Earth’s surface, where the oscillatory mode of the geomagnetic field disturbance is observed, are analyzed. The electron concentration and conductivity in the lower ionosphere, as well as the characteristics of the heat source and the Ampère force, which result from a change in the electric current, are calculated. The generation of an acoustic-gravity wave pulse by these sources in the lower ionosphere is considered. The propagation of these waves in the conducting ionosphere is accompanied by a perturbation of the electric current and magnetic field. The calculation of time dependence of the magnetic field is carried out, the results of which are compared with magnetograms. It is shown that this model can be used to interpret the data on recording of geomagnetic field fluctuations in the range of 5–10 min.

Appendices

APPENDIX A

The electric and geomagnetic fields in the conducting ionosphere moving at a speed V are determined from Maxwell’s equations:

$$\nabla \times {\mathbf{E}} = - \frac{{\partial {\mathbf{B}}}}{{\partial t}},\,\,\,\,\nabla \times {\mathbf{B}} = {{\mu }_{0}}\hat {\sigma }\left( {{\mathbf{E}} + {{{\mathbf{E}}}_{d}}} \right) + {{\mu }_{0}}{{\varepsilon }_{0}}\frac{{\partial {\mathbf{E}}}}{{\partial t}},$$

where ${{{\mathbf{E}}}_{d}} = {\mathbf{V}} \times {\mathbf{B}}$ is the constant electric dynamo field. In the absence of nonstationary disturbances, the constant and potential electric field ${{{\mathbf{E}}}_{0}}$ satisfies the equations

$$\nabla \cdot \hat {\sigma }\left( {{{{\mathbf{E}}}_{0}} + {{{\mathbf{E}}}_{d}}} \right) = 0,\,\,\,\,\nabla \cdot {{{\mathbf{E}}}_{0}} = 0.$$

A nonstationary perturbation of the conductivity generates an additional electric field ${{{\mathbf{E}}}_{1}} = {\mathbf{E}} - {{{\mathbf{E}}}_{0}},$ which, in the quasi-stationary approximation, satisfies the equation

$$\nabla \times \left( {\nabla \times {{{\mathbf{E}}}_{1}}} \right) + {{\mu }_{0}}\frac{\partial }{{\partial t}}\left( {\hat {\sigma }{{{\mathbf{E}}}_{1}}} \right) = - {{\mu }_{0}}\left( {\frac{{\partial \hat {\sigma }}}{{\partial t}}} \right)\left( {{{{\mathbf{E}}}_{0}} + {{{\mathbf{E}}}_{d}}} \right).$$

After the end of the transient process caused by a nonstationary perturbation of the conductivity ${\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} = 0,$ we obtain the equality $\nabla \times \left( {\nabla \times {{{\mathbf{E}}}_{1}}} \right) = 0.$ The electric field perturbation at infinity is zero, consequently, we have ${{{\mathbf{E}}}_{1}} = 0.$ Thus, for slow processes, it can be believed that the geoelectric field coincides with the field in the unperturbed state ${\mathbf{E}} = {{{\mathbf{E}}}_{0}}.$ The characteristic duration of the transient process is $\tau = {{\mu }_{0}}\sigma {{L}^{2}},$ where $L$ is the characteristic spatial scale of the process. Assuming $\sigma \sim {{10}^{{ - 4}}}\,\,{{\text{S}} \mathord{\left/ {\vphantom {{\text{S}} {\text{m}}}} \right. \kern-0em} {\text{m}}}$, $L \sim {{10}^{5}}\,\,{\text{m}}$, we obtain $\tau \sim 1\,\,{\text{s}}$. Since in this paper we consider processes with characteristic times greater than $100\,\,{\text{s}}$, we will use the approximation ${\mathbf{E}} = {{{\mathbf{E}}}_{0}}.$

Ohm’s law in the ionosphere has the form ${\mathbf{j}} = \hat {\sigma }{\mathbf{E}}.$ The ionosphere conductivity tensor $\hat {\sigma }$ in the accepted coordinate system is determined by the matrix

$$\hat {\sigma } = \left( {\begin{array}{*{20}{c}} {{{\sigma }_{l}}{{{\sin }}^{2}}\alpha + {{\sigma }_{P}}{{{\cos }}^{2}}\alpha }&{ - {{\sigma }_{H}}\cos \alpha }&{ - \left( {{{\sigma }_{l}} - {{\sigma }_{P}}} \right)\cos \alpha \sin \alpha } \\ {{{\sigma }_{H}}\cos \alpha }&{{{\sigma }_{P}}}&{{{\sigma }_{H}}\sin \alpha } \\ { - \left( {{{\sigma }_{l}} - {{\sigma }_{P}}} \right)\cos \alpha \sin \alpha }&{ - {{\sigma }_{H}}\sin \alpha }&{{{\sigma }_{l}}{{{\cos }}^{2}}\alpha + {{\sigma }_{P}}{{{\sin }}^{2}}\alpha } \end{array}} \right),$$

where ${{\sigma }_{{l,P,H}}}$ is the longitudinal conductivity and the Pedersen and Hall conductivities, respectively.

Let us take the horizontally homogeneous approximation (in which ${{\partial }_{{x,y}}} \approx 0$), which is valid due to the large horizontal scales of ionospheric disturbances generated by solar flares. In this approximation, the current continuity equation $\nabla \cdot {\mathbf{j}} = 0$ has the form ${{d{{j}_{z}}} \mathord{\left/ {\vphantom {{d{{j}_{z}}} {dz}}} \right. \kern-0em} {dz}} = 0,$ ${{j}_{z}} = {\text{const}}(z).$ Since at the lower boundary of the ionosphere ${{j}_{z}} = 0,$ then in the ionosphere ${{j}_{z}} = 0.$ This condition in Ohm’s law determines the relationship between the vertical and horizontal components of the electric field:

$${{E}_{z}} = - \frac{{ - \left( {{{\sigma }_{l}} - {{\sigma }_{P}}} \right)\cos \alpha \sin \alpha {{E}_{x}} - {{\sigma }_{H}}\sin \alpha {{E}_{y}}}}{{{{\sigma }_{l}}{{{\cos }}^{2}}\alpha + {{\sigma }_{P}}{{{\sin }}^{2}}\alpha }}.$$

Substituting this equality into Ohm’s law for the horizontal components of the current density vector, we get

$${{{\mathbf{j}}}_{ \bot }} = {{\hat {\sigma }}_{ \bot }}{{{\mathbf{E}}}_{ \bot }},\,\,\,\,{{\hat {\sigma }}_{ \bot }} = \left( {\begin{array}{*{20}{c}} {{{\sigma }_{{xx}}}}&{{{\sigma }_{{xy}}}} \\ {{{\sigma }_{{yx}}}}&{{{\sigma }_{{yy}}}} \end{array}} \right),$$

where components of the tensor ${{\hat {\sigma }}_{ \bot }}$ have the form

$$\begin{gathered} {{\sigma }_{{xx}}} = \frac{{{{\sigma }_{P}}{{\sigma }_{l}}}}{{{{\sigma }_{l}}{{{\cos }}^{2}}\alpha + {{\sigma }_{P}}{{{\sin }}^{2}}\alpha }}, \\ {{\sigma }_{{xy}}} = - \frac{{{{\sigma }_{H}}{{\sigma }_{l}}\cos \alpha }}{{{{\sigma }_{l}}{{{\cos }}^{2}}\alpha + {{\sigma }_{P}}{{{\sin }}^{2}}\alpha }}, \\ {{\sigma }_{{yx}}} = - {{\sigma }_{{xy}}},\,\,\,\,{{\sigma }_{{yy}}} = {{\sigma }_{P}} + \frac{{\sigma _{H}^{2}{{{\sin }}^{2}}\alpha }}{{{{\sigma }_{l}}{{{\cos }}^{2}}\alpha + {{\sigma }_{P}}{{{\sin }}^{2}}\alpha }}. \\ \end{gathered} $$

In the ionosphere at heights $z > 80\,\,{\text{km}}$, the condition ${{\sigma }_{l}} \gg {{\sigma }_{{P,H}}}$ is satisfied. Consequently, for angles $\alpha ,$ not too close to $90^\circ ,$ i.e., except for the region near the equator, the conductivity tensor ${{\hat {\sigma }}_{ \bot }}$ has the form

$${{\hat {\sigma }}_{ \bot }} = \left( {\begin{array}{*{20}{c}} {\frac{{{{\sigma }_{P}}}}{{{{{\cos }}^{2}}\alpha }}}&{ - \frac{{{{\sigma }_{H}}}}{{\cos \alpha }}} \\ {\frac{{{{\sigma }_{H}}}}{{\cos \alpha }}}&{{{\sigma }_{P}}} \end{array}} \right).$$

It should be noted that the inequality ${{\sigma }_{l}} \gg {{\sigma }_{{P,H}}}$ leads to the condition that the longitudinal component of the electric field vanishes ${{E}_{\parallel }} = {{E}_{x}}\sin \alpha + {{E}_{z}}\cos \alpha = 0.$

APPENDIX B

Equation (15) will be solved by the Green’s function method. We represent the function $u\left( {z,t} \right)$ as a convolution of the Green’s function and the source

$$u\left( {z,t} \right) = - \int\limits_0^t {dt{\kern 1pt} '} \int\limits_{ - \infty }^\infty {dz{\kern 1pt} 'G\left( {z - z{\kern 1pt} ',t - t{\kern 1pt} '} \right)U\left( {z{\kern 1pt} ',t{\kern 1pt} '} \right).} $$

Under the integral, the following function is denoted:

$$U\left( {z,t} \right) = \frac{1}{{a{{\rho }_{0}}\left( 0 \right)}}\exp \left( {\frac{z}{{2H}}} \right)F(z,t).$$

The Green’s function $G\left( {z,t} \right)$ is determined from the equation

$$\frac{{{{\partial }^{2}}G}}{{\partial {{z}^{2}}}} - \frac{1}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}G}}{{\partial {{t}^{2}}}} - \frac{1}{{4{{H}^{2}}}}G = - \frac{1}{a}\delta \left( z \right)\delta \left( t \right),$$

where $\delta \left( x \right)$ is the Dirac delta function. To solve this equation, we apply the Laplace transform in time to it:

$$\tilde {G}\left( {z,s} \right) = \int\limits_0^\infty {G\left( {z,t} \right)\exp \left( { - st} \right)dt} .$$

Using the initial conditions for the Green’s function:

$$G\left( {z,0} \right) = 0,\,\,\,\,{{\left. {\frac{{\partial G}}{{\partial t}}} \right|}_{{t{\kern 1pt} = {\kern 1pt} 0}}} = a\delta \left( z \right),$$

we obtain the equation for the Laplace image of the Green’s function:

$$\frac{{{{d}^{2}}\tilde {G}}}{{d{{z}^{2}}}} - \frac{1}{{{{a}^{2}}}}({{s}^{2}} + \omega _{a}^{2}){\kern 1pt} \tilde {G} = - \frac{2}{a}\delta \left( z \right),\,\,\,\,{{\omega }_{a}} = {a \mathord{\left/ {\vphantom {a {2H.}}} \right. \kern-0em} {2H.}}$$

From this equation, the boundary conditions follow

$${{\left. {\left\{ {\tilde {G}} \right\}} \right|}_{{z{\kern 1pt} = {\kern 1pt} 0}}} = 0,\,\,\,\,{{\left. {\left\{ {\frac{{d\tilde {G}}}{{dz}}} \right\}} \right|}_{{z{\kern 1pt} = {\kern 1pt} 0}}} = - \frac{2}{a},$$

where the braces denote the jump of the corresponding value at $z = 0.$ Using the boundary conditions, we obtain the solution to the equation for the Laplace image of the Green’s function, decreasing at $\left| z \right| \to \infty ,$ in the form

$$\tilde {G}\left( {z,s} \right) = \frac{{\exp \left[ { - \frac{{\left| z \right|}}{a}\sqrt {\omega _{a}^{2} + {{s}^{2}}} } \right]}}{{\sqrt {\omega _{a}^{2} + {{s}^{2}}} }}.$$

Performing the inverse Laplace transform (Bateman and Erdelyi, 1969), we obtain the Green’s function of equation (15):

$$G\left( {z,t} \right) = {{J}_{0}}\left[ {{{\omega }_{a}}\sqrt {{{t}^{2}} - {{{\left( {{z \mathord{\left/ {\vphantom {z a}} \right. \kern-0em} a}} \right)}}^{2}}} } \right]\eta \left( {t - {{\left| z \right|} \mathord{\left/ {\vphantom {{\left| z \right|} a}} \right. \kern-0em} a}} \right),$$

where ${{J}_{0}}\left( x \right)$ is the Bessel function, $\eta \left( x \right)$ is the Heaviside function. Consequently, the solution of equation (13) has the form

$$\begin{gathered} {v}\left( {z,t} \right) = - \frac{{\exp \left( {{z \mathord{\left/ {\vphantom {z {2H}}} \right. \kern-0em} {2H}}} \right)}}{{a{{\rho }_{0}}\left( 0 \right)}} \\ \times \,\,\int\limits_0^t {dt{\kern 1pt} '} \int\limits_{ - \infty }^\infty {dz{\kern 1pt} '} G\left( {z - z{\kern 1pt} ',t - t{\kern 1pt} '} \right)\exp \left( {{{z{\kern 1pt} '} \mathord{\left/ {\vphantom {{z{\kern 1pt} '} {2H}}} \right. \kern-0em} {2H}}} \right)F(z{\kern 1pt} ',t{\kern 1pt} '), \\ G\left( {z,t} \right) = {{J}_{0}}\left[ {{{\omega }_{a}}\sqrt {{{t}^{2}} - {{{\left( {{z \mathord{\left/ {\vphantom {z a}} \right. \kern-0em} a}} \right)}}^{2}}} } \right]\eta \left( {t - {{\left| z \right|} \mathord{\left/ {\vphantom {{\left| z \right|} a}} \right. \kern-0em} a}} \right), \\ \end{gathered} $$

where $H$ is the height of the homogeneous atmosphere, $a$ is the speed of sound, ${{\omega }_{a}} = {a \mathord{\left/ {\vphantom {a {2H}}} \right. \kern-0em} {2H}};$ ${{\rho }_{0}}\left( 0 \right)$ is the air density on the Earth’s surface, ${{E}_{x}},{{E}_{y}}$ are the components of the background electric field, $\alpha$ is the angle between the geomagnetic field vector and the positive direction of the axis $z.$