The oil reservoir can contain both interlayers of super reservoirs with the permeability that is higher than the permeability of the remaining part of the reservoir by hundreds and thousands times, as well as high-conducting channels induced by regional fracturing in a definite direction. When the water injection pressure becomes higher than a critical value, the reservoir hydraulic fracture or hydraulic fracturing in the injection well takes place. This reduces to zero the advantages of the water flooding technology. Injected water rapidly breaks through into the producing wells leading to considerable water cut in the production and reduction in the flooding sweep efficiency coefficient of the reservoir. Examples of such development of events in flooding are the presence of the super reservoir on Talin field [1], the development of hydraulic fractures in the injection wells in the Priobskoye oil deposit [2] and a series of other cases.

The treatments that impede such a development of events are the so-called conformance improvement technologies [3]. The base of these technologies is injection of reactants, first of all, suspensions which can penetrate into high-conducting channels and fractures but cannot flow through the main porous mass of the reservoir.

In the present study the problem of partial or complete blocking of the hydraulic fracture in the injection well is considered. Usually, the determination of the pressure of formation of hydraulic fracture in the injection well is carried out with the use of two-step flow rate test [4]. In the course of this test, in going over from one step to the other the flow rate of injected water varies and the bottomhole pressure dynamics are measured. Tracing the dynamics of development of hydraulic fracture in the injection well` and estimating its parameters is implemented in the course of recording the continuous curve of variation in the pressure in time in the process of change in the well operation regimes [5]. Under the field conditions, the onset and development of the hydraulic fracture in the injection well can be controlled using the well interference testing [6]. More complete information on formation of the hydraulic fracture in the injection well can be found in the core sample investigations, for example, by means of the Brazil test [7] during which the core sample is compressed in the plane of diameter.

The investigations on the core sample do not make it possible to trace in detail the dynamics of development of the hydraulic fracture in the injection well at large scales; therefore, the mathematical simulation of this process is topical. In [8] it was proposed a semianalytical model of propagation of the hydraulic fracture in the injection well based on the Biot theory of stressed state [9] that determined the fracture development regime. Moreover, a series of studies [10–12] were devoted to application of the geomechanical approach to determination of the hydraulic fracture dimensions. There exist three-dimensional models [13] to describe the dynamics of development of the hydraulic fracture based on this approach. In [11] it was noted that the reagent injection rate into the hydraulic fracture affects its shape. The geomechanical approach also makes it possible to estimate the interaction between a hydraulic fracture and the natural fractures in the reservoir [14]. As a whole, such an approach makes it possible to find the parameters of a hydraulic fracture or the hydraulic fracture in the injection well and predict its development but it does not describe the motion of fluid through the fracture.

The approaches of mechanics of multiphase systems found a wide application to the problems of displacement of one fluid by another one in the porous medium [15–17]. The development of these approaches with regard to the elliptical external boundary makes it possible to solve the problem of fluid inflow to the well in the presence of the hydraulic fracture [18]. Moreover, there exist mathematical models that describe fluid flow through the fracture under the action of the electromagnetic field [19]. However, the considered models do not describe blocking the hydraulic fracture in the injection well which may be necessary to prevent water inflow to reactive producing wells to reduce the water cutting of production. The solution of this problem is first given in the present study.

To estimate the effect of the fracture parameters on the water cutting of the surrounding producing wells it is necessary to consider the sector reservoir model in the neighborhood of the fracture. In accordance with the field data, as a result of formation of hydraulic fractures in the injection well, the effectiveness of water injection can reduce to 50% due to fast water breakthrough along the fracture [20]. To estimate the effect of the hydraulic fractures in the injection well, it was in [21] introduced the dimensionless parameter of the flooding effectiveness. This coefficient shows the ratio of the volume of injected water in the ideal case, calculated from the material balance equation, to the actual volume of water injection.

The fracture blocking models consider fluid flow through the fracture with regard to reagent transport and water outflow from the side walls of the fracture into the reservoir. As a rule, one-dimensional flows are considered both inside the fracture and in the reservoir. In [22] the model of blocking the fracture using a gel-forming composition in which the coordinate of the front of injected gel in the fracture is calculated from the material balance equation. The model also makes it possible to determine the fracture permeability with regard to the presence of the gel in the fracture.

The more complex models that can be used to describe the process under consideration consider the placing, for example, of the propping agent in the hydraulic fracture as suspension flow [23–25]. In the present study the development of this approach to describe the process of blocking a technogenic fracture by a polymer-disperse suspension mixture. Such a description is first presented. As the disperse particles, particles of clay, chalk, or wood dust are used [26].

1 MATHEMATICAL MODEL OF BLOCKING THE FRACTURE USING A SUSPENSION COMPOSITION

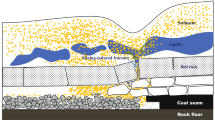
We will consider the problem of linear one-dimensional suspension flow through a rectangular fracture of length l, width w, and height h (Fig. 1). The fracture is located in the neighborhood of an injection well. On the external fracture boundary L (half the distance between the lateral fracture boundary and the nearest reactive producing well) the pressure is equal to pr, on the fracture end the pressure is unknown and is defined by the variable pf. Suspension is injected at the constant bottomhole pressure pw and moves along the fracture at a velocity v. The outflow of fluid from the fracture through the lateral fracture surfaces is denoted by the variable q. The Cartesian rectangular coordinate system with the x axis directed along the fracture and the y axis which is perpendicular to it is introduced.

Fig. 1.
figure 1

Schematic representation of the problem of blocking the hydraulic fracture in the injection well.

Full size image

Suspension consists of rigid particles stabilized in the water phase with a polymer admixture or soft polymeric gel. The volume particle content in flow is equal to α and the total suspension flow rate along the fracture is equal to Q = hw\({v}\). The absence of the mechanisms of particle trapping is characteristic for the fracture. The flow is considered in the homogeneous approximation or as advective flow in which the velocities of the particles and the carrier phase are identical. The carrier fluid moves along the fracture and flows out to the reservoir owing to the difference between the reservoir and fracture pressures, the carrier fluid outflow q takes place through both lateral walls of the fracture. Taking these assumptions into account, the particle and carrier fluid mass conservation equations take the form:

$$\frac{{\partial \left( {hw\alpha } \right)}}{{\partial t}} + \frac{{\partial \left( {hw\alpha {v}} \right)}}{{\partial x}} = 0,$$
(1.1)
$$\frac{{\partial \left( {hw\left( {1 - \alpha } \right)} \right)}}{{\partial t}} + \frac{{\partial \left( {hw\left( {1 - \alpha } \right){v}} \right)}}{{\partial x}} = - q,$$
(1.2)

where t is time.

The motion of suspension along the fracture is considered in the inertia-free approximation in which the momentum conservation equation can be written from the solution of the problem of viscous fluid in laminar flow in a parallelepiped. This solution takes the form:

$${v} = - \frac{{{{w}^{2}}}}{{12\mu }}\frac{{\partial p}}{{\partial x}},$$
(1.3)

where μ is the carrier phase viscosity and p is the fracture pressure.

The carrier fluid outflow in the reservoir is also assumed to be linear but it occurs in the perpendicular direction and is determined from Darcy’s law

$$q = \frac{{k{{h}_{e}}}}{{\mu L}}\left( {p - {{p}_{r}}} \right),$$
(1.4)

where k is the reservoir permeability and he is the effective thickness of reservoir (except for the clay interlayers).

The problem considered can be split into two problems, namely, determination of the pressure distribution in the fracture and particle transport through the fracture.

2 PRESSURE DISTRIBUTION IN THE FRACTURE

The first problem is determined by the equation for the total suspension flow or the sum of Eqs. (1.1) and (1.2) in which we must substitute the expressions for flow velocities along the fracture and outflow into the reservoir

$$\frac{{{{d}^{2}}p}}{{d{{x}^{2}}}} = \frac{{12k{{h}_{e}}}}{{{{w}^{3}}Lh}}\left( {p - {{p}_{r}}} \right).$$
(2.1)

To solve this equation it is necessary to have two boundary conditions. The first boundary condition is determined by the constant pressure in suspension injection into the fracture. As the second condition, we take the equality of the inflow supplied to the fracture and the integral fluid outflow into the reservoir

$$x = 0:p = {{p}_{w}},\quad - {{\left. {\frac{{\partial p}}{{\partial x}}} \right|}_{{x = 0}}} = \frac{{24k{{h}_{e}}}}{{\left( {1 - {{\alpha }_{0}}} \right){{w}^{3}}Lh}}\int\limits_0^l {\left( {p - {{p}_{r}}} \right)} dx,$$
(2.2)

where α0 is the volume fraction of disperse particles in the injected suspension.

These boundary conditions hold so far the suspension particles do not reach the fracture end. After this instant the fracture begins to be blocked from the end and its size reduces to the variable quantity xf. Respectively, the upper limit of the integral in the boundary condition (2.2) becomes to be equal to xf.

The solution of the differential equation (2.1) with regard to the boundary conditions (2.2) takes the form:

$$p = \frac{{{{p}_{f}} - {{p}_{r}} - a\Delta p}}{{1 - {{a}^{2}}}}{{a}^{{ - \left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} - 1} \right)}}} + \frac{{a\left( {{{p}_{r}} - {{p}_{f}}} \right) + \Delta p}}{{1 - {{a}^{2}}}}{{a}^{{{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}} + {{p}_{r}},$$
(2.3)

where we introduced the notation \(\Delta p = {{p}_{w}} - {{p}_{r}}\) and \(a = \exp ( - l\sqrt {{{12k{{h}_{e}}} \mathord{\left/ {\vphantom {{12k{{h}_{e}}} {({{w}^{3}}Lh)}}} \right. \kern-0em} {({{w}^{3}}Lh)}}} )\).

At the fracture end the pressure can be determined by substituting the expression (2.3) in the second boundary condition (2.2):

$${{p}_{f}} = \frac{{D\left( {\Delta p + 2{{p}_{r}}a + a\Delta p} \right) + 2{{p}_{r}} - {{p}_{w}}}}{{1 + 2Da}}.$$
(2.4)

In formula (2.4) we introduced the dimensionless complex \(D = \frac{{h\left( {1 - {{\alpha }_{0}}} \right)}}{{2{{h}_{e}}{{{\left( {1 - a} \right)}}^{2}}}},\) that characterizes the extent of the pressure drop in the fracture depending on the relation between the reservoir and fracture transmissibilities.

3 MAIN EFFECTS IN INJECTION OF A SUSPENSION SLUG INTO THE FRACTURE

We will consider the case of injection of a suspension consisting of clay particles and an aqueous polyacrylamide solution that prevents the gravity segregation of suspension in the well and fracture. The calculations were carried out for model values of the reservoir, fracture and suspension parameters, namely, k = 100 mD, α0 = 0.03, w = 2 mm, l = 200 m, L = 500 m, μ = 1 mPa s, pw = 35 MPa, pr = 25 MPa, h = 40 m, and he = 30 m.

In addition to the pressure distribution in the fracture, of interest is the fluid outflow from the fracture and the suspension flow rate through the fracture. These parameters can be obtained from solution (2.3) by substituting it in formulas (1.3) and (1.4).

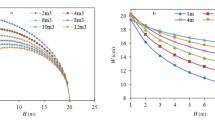
Depending on the value of the introduced dimensionless parameter D, the following scenarios are possible. When D > 1, as the suspension is injected, the carrier fluid travels along the fracture and partially moves outward into the porous reservoir. The pressure along the fracture, the intensity of the carrier fluid outflow into the reservoir, and the suspension velocity decrease monotonically with increase in the distance from the well. In Fig. 2a we have reproduced the results of calculations of the fracture pressure and the carrier phase outflow rate and in Fig. 2b—the suspension flow rate in the fracture.

Fig. 2.
figure 2

Distribution of the pressure p in the fracture (curve 1) and outflow of the carrier fluid into the reservoir q (curve 2) at D > 1 (a); suspension flow rate Q along the fracture (b).

Full size image

At the high reservoir permeability and the parameter D < 1 the fracture pressure can decrease and become lower than the reservoir pressure, then a fluid inflow into the reservoir is observed at the fracture end. In Fig. 3 we have given an example of such a calculation in which the reservoir permeability was taken to be equal to 160 D or 1.6 × 10–10 m2 and the parameter D becomes less than unity. In this case the suspension flow rate in the facture becomes nonmonotonic: its decrease occurs in the beginning of the fracture and, to the contrary, the suspension flow rate begins to grow (Fig. 3b) in the region of reduction in the fracture pressure to values less than the reservoir pressure (Fig. 3a).

Fig. 3.
figure 3

Distribution of the pressure p in the fracture (curve 1) and outflow of the carrier fluid into the reservoir q (curve 2) at D < 1 (a); suspension flow rate Q along the fracture (b).

Full size image

4 MOTION OF A SLUG THROUGH THE FRACTURE AND ITS BLOCKING

The second problem consists in the determination of evolution of the slug of suspension particles. When the expression for the suspension flow velocity in the fracture (1.3) is known, the suspension particle transport equation (1.1) can be represented with regard to (2.3) in the characteristic form:

$$\frac{{dx}}{{dt}} = {v}:\,\frac{{d\alpha }}{{dt}} = - \alpha \frac{{d{v}}}{{dx}}.$$
(4.1)

In accordance with this solution, the leading front of suspension slug represents a contact discontinuity which moves at a variable velocity and whose trajectory can be determined from the formula

$$t = \frac{{wLh\mu (1 - {{a}^{2}})}}{{k{{h}_{e}}\sqrt { - \gamma \beta } }}\left( {\ln \left| {\frac{{1 + \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} {{a}^{{ - {x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}}}}{{1 - \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} {{a}^{{ - {x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}}}}} \right| - \ln \left| {\frac{{1 + \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} }}{{1 - \sqrt { - {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0em} \gamma }} }}} \right|} \right),$$

where we introduced the notation \(\beta = \left( {{{p}_{r}} - {{p}_{f}}} \right)a + {{a}^{2}}\Delta p\) and \(\gamma = \Delta p + \left( {{{p}_{r}} - {{p}_{f}}} \right)a\).

In Fig. 4a we have plotted the calculated trajectory for the above parameters. Along this trajectory the volume content of particles increases due to the carrier fluid outflow into the reservoir. The solution for evolution of the volume fraction of particles on the front takes the form:

$$\alpha = {{\alpha }_{0}}\exp \left( { - \frac{{k{{h}_{e}}t}}{{wLh\mu (1 - {{a}^{2}})}}(\left( {{{p}_{r}} - {{p}_{f}}} \right)({{a}^{{ - \left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} - 1} \right)}}} - {{a}^{{\left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} + 1} \right)}}}) + \Delta p({{a}^{{ - \left( {{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l} - 2} \right)}}} - {{a}^{{{x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}}}}))} \right).$$
Fig. 4.
figure 4

Trajectory of motion of the contact discontinuity that correspond to the leading front of slug (a); trajectory of the discontinuity that separates the blocked fracture zone and the suspension inflow zone (b).

Full size image

In the realistic case of the low-permeability reservoir, just in which the hydraulic fractures in the injection well mainly develop, the volume fraction of particles on the contact front increases monotonically, while the velocity of the front decreases. This case is given in Fig. 5a.

Fig. 5.
figure 5

Motion of the suspension slug along the fracture at D > 1 (a); motion of the suspension slug along the fracture at D < 1 (b). In Fig. 5 (a) we have plotted curves at the following instants of time: 100 (curve 1), 300 (curve 2), 500 s (curve 3) and the instant t0 (curve 4) at which the front of the volume fraction of disperse particles reaches the right boundary of the fracture. In Fig. 5,b we have plotted curves at the following instants of time: curve 1 corresponds to 1.25 s, curve 2 to 2.5 s, curve 3 to 3.75 s, curve 4 to 6 s, curve 5 to 7 s, curve 6 to 8 s, and curve 7 to the instant t0 at which the front of the volume fraction of disperse particles reaches the right boundary of the fracture.

Full size image

In the case D < 1 propagation of the front slows down gradually and the volume fraction of disperse particles on the front increases, while the carrier phase flows out into the reservoir and the fracture pressure is higher than the reservoir pressure. As soon as the fracture pressure becomes lower than the reservoir pressure (Fig. 3a), the carrier phase begins to flows into the fracture. For this reason, the volume fraction of disperse particles on the front drops (Fig. 5b), the motion of the front being accelerated (Fig. 5b) by virtue of increase in the flow velocity in the fracture.

The principal feature of the process is the establishment of a stationary distribution of the volume fraction of disperse particles in the fracture at the instant of approach of the front to the fracture end. In what follows, this feature will be used to simplify the procedure of obtaining the semianalytic solution.

At t = to, at the instant of approach of the contact discontinuity to the fracture end x = l, a discontinuity of the volume fraction of particles, in which ahead of the discontinuity front α = α– and behind the discontinuity α = 1, is formed. Ahead of the discontinuity, the volume fraction of particles α– is determined from the solution of the characteristic system (4.1). The developed discontinuity moves as the reflected wave counter the stream and the relations on the discontinuity takes the form:

$$(1 - {{\alpha }^{ - }})\frac{{d{{x}_{f}}}}{{dt}} + {{{v}}^{ - }}{{\alpha }^{ - }} = 0,$$
(4.2)

where \({{{v}}^{ - }}\) is the velocity ahead of the discontinuity.

After this instant, the pressure pf  on the front of blocked zone xf  becomes the quantity that depends on time. The implicit time dependence appears in integration of the edge condition (2.2) on the interval from 0 to xf. After substitution of the result of integration over the variable interval in (4.2), we can obtain an equation for determining xf  as a function of time. Unfortunately, this procedure is extremely cumbersome; therefore, the solution for α– is approximated by the following quadratic function with square of the correlation coefficient R2 = 0.9992

$${{\alpha }^{ - }} = {{F}_{1}}{{x}^{2}} + {{F}_{2}}x + {{\alpha }_{0}},$$

where F1 and F2 are numerical coefficients. In the case considered they are equal to F1 = 4 × 10–7 1/m2 and F2 = 5 × 10–5 1/m.

The solution of Eq. (4.2) under the condition xf(t0) = l takes the form:

$$t = \int\limits_l^{{{x}_{f}}} {\frac{{(1 + 2{{e}^{{ - M{{x}_{f}}}}}\left( {B - 1} \right) + {{e}^{{ - 2M{{x}_{f}}}}})({{F}_{1}}x_{f}^{2} + {{F}_{2}}{{x}_{f}} + {{\alpha }_{0}} - 1)}}{{G(1 - {{e}^{{ - 2M{{x}_{f}}}}})({{F}_{1}}x_{f}^{2} + {{F}_{2}}{{x}_{f}} + {{\alpha }_{0}})}}d{{x}_{f}}} ,$$
(4.3)

where we introduced the notation \(G = \sqrt {{{kw{{h}_{e}}} \mathord{\left/ {\vphantom {{kw{{h}_{e}}} {\left( {12Lh} \right)}}} \right. \kern-0em} {\left( {12Lh} \right)}}} {{\Delta p\left( {1 - B} \right)} \mathord{\left/ {\vphantom {{\Delta p\left( {1 - B} \right)} \mu }} \right. \kern-0em} \mu }\), \(M = \sqrt {{{12k{{h}_{e}}} \mathord{\left/ {\vphantom {{12k{{h}_{e}}} {({{w}^{3}}Lh)}}} \right. \kern-0em} {({{w}^{3}}Lh)}}} \), and B = \({{h(1 - {{\alpha }_{0}})} \mathord{\left/ {\vphantom {{h(1 - {{\alpha }_{0}})} {(2{{h}_{e}})}}} \right. \kern-0em} {(2{{h}_{e}})}}\).

The integral (4.3) can be determined numerically, for example, using the trapezoidal method. In Fig. 4b we have reproduced the calculation results of discontinuity dynamics xf(t). As can be seen from the graph obtained, the velocity of discontinuity or extension of the region of blocking the fracture gradually slows down. Slowing down of the discontinuity or the front of blocking the fracture grows up fairly rapidly. This indicates to the problematical character of complete blocking of the fracture.

SUMMARY

The problem of blocking the hydraulic fracture in the injection well using a suspension of particles whose sizes are greater than the sizes of collector pores. This makes it possible to advance the suspension slug to the fracture end and then begin blocking the fracture.

It is established that for the high-permeability reservoir a scenario in which the carrier phase flows out in the porous stratum in the beginning of fracture is possible, whereas the reservoir fluid flows into the fracture closer to its end. The dimensionless similarity criterion at which this scenario can be implemented is found.

The structure of solution of the problem of blocking the fracture is revealed. In the first stage the suspension moves with slowing down but fairly rapidly through the fracture and reaches its end. In the second stage a reflected wave in form of a discontinuity is formed. Blocking the fracture occurs on this discontinuity. The velocity of the discontinuity decreases. This demonstrates the problematical character of complete blocking of the fracture.

The analytical solutions are obtained using the characteristics method and the relation on the discontinuity in all stages of the process.