Development of Disturbances in a Circular Submerged Jet with Two Instability Modes

Abstract

The stability and nonlinear interaction between the disturbances in a round jet are investigated numerically at Re = 2850. The conditions of the laboratory experiment performed earlier in the Institute of Mechanics of Moscow State University are reproduced. The characteristic feature of the jet considered is the presence of three points of inflection in the inflow velocity profile. This fact determines essentially the properties of flow. Linear stability is investigated using two approaches: quasi-parallel and spatial. Good quantitative agreement between the results of two approaches and adequate agreement with the results of inviscid theory are obtained. Numerical calculations are carried out with the aim to explain and interpret the results of the laboratory experiment in which change in the length of the laminar-turbulent transition zone in the jet under the action of time-periodic axisymmetric perturbations is revealed. It is shown that axisymmetric disturbances of even considerable initial amplitude do not lead to laminar-turbulent transition. The transition observed experimentally is attributable to the presence of non-controlled three-dimensional disturbances that are strengthened against the background of fairly intense artificial disturbances. The investigations carried out in the present study confirm this hypothesis. Thus, the three-dimensional disturbances serve as an initiator of transition, while the axisymmetric disturbances of a fairly high amplitude only accelerate their growth. It is shown that more intense three-dimensional disturbances are able to ensure still more rapid transition even in the absence of axisymmetric component.

Widespread distribution of jet flows in the natural systems and technical devices stimulates interest of engineers and reseachers to studying various phenomena related to their development. For example, jet turbulization modifies significantly the processes of heat- and mass exchange with the surrounding medium; therefore, studying the processes of laminar-turbulent transition in jets is extremely urgent, in particular, with the aim to search the resources to control transition for obtaining the optimum solutions and increasing the effectiveness of technological processes. The process of laminar-turbulent transition in jets depends significantly on both the flow perturbation level at the nozzle exit section and the shape of the mean velocity profile in the inlet stream. Laminar jet flows lose stability already at very low Reynolds numbers [1–3]. At large ${\text{Re}} \sim {{10}^{3}}{\kern 1pt} - {\kern 1pt} {{10}^{4}}$, turbulence transition in circular jets occurs, as a rule, in the immediate neighborhood of the nozzle exit section, within the distance of 1D (D is the nozzle diameter). Several years ago, a compact device for generation of circular air jets which ensures maintenance of laminar flow at ${\text{Re}} = {{U}_{b}}R{\text{/}}\nu < 6000$ (U_b is the mean velocity in the inlet stream, $R = D{\text{/}}2$) at distances to ~6D at D = 0.12 m was designed and fabricated in the Institute of Mechanics of Moscow State University [4, 5]. In this case, the dimension of the device is equal to approximately only $1.5D$. The characteristic feature of the jets generated by the device at various Reynolds numbers is the presence of two modes of unstable perturbations which differ significantly with respect to their growth rates in propagating downstream [6, 7]. In introducing artificial axisymmetric perturbations, it was revealed that the length of the jet laminar section depends on the perturbation frequency reaching the minimum at frequencies that correspond to the maximum growth of small perturbations. It was also found that introduction of three-dimensional artificial perturbations leads to significantly more rapid turbulence transition [8].

In the present study the development of perturbations in the circular jet is simulated numerically under the conditions similar to experimental conditions. The details of linear evolution and nonlinear interaction between the perturbations that corespond to various instability modes are studied. Detailed comparison with the experiment is given.

1 FORMULATION AND METHOD FOR SOLVING THE PROBLEM

We will consider the problem of viscous imcompressible fluid flow out from a circular orifice of radius $R$ (nozzle exit section) in half-space {x > 0} in the plane {x = 0}. The properties of the surrounding medium are the same as those of the flowing-out jet. The time-dependent velocity field $\mathbf{u}(t,\mathbf{x})$ (t is time and x is a point in space) can be found by solving numerically the Navier–Stokes equations

$$\frac{{\partial \mathbf{u}}}{{\partial t}} + (\mathbf{u}\nabla )\mathbf{u} = - \nabla p + \nu {{\nabla }^{2}}\mathbf{u},\quad \nabla \mathbf{u} = 0.$$

(1.1)

Here, p is the kinematic pressure and $\nu$ is the fluid viscosity.

The problem is solved in the cylindrical coordinate system $\mathbf{x} = (x,r,\theta )$ in the cylindrical computational domain $\{ 0 < x < {{X}_{m}},\;r < {{R}_{m}}\}$. The radius R_m of the computational domain is significantly greater than the nozzle radius. In the nozzle exit section we specify the time-dependent velocity field (inlet boundary conditions) $\mathbf{u}(x = 0,r \leqslant R) = {\mathbf{U}_{0}}(t,r,\theta )$. The no-flow and free slip conditions are imposed on the remaining inlet cross-sectional area $\{ x = 0,\;r > R\}$ and on the cylindrical boundary of the computational domain $\{ x > 0,\;r = {{R}_{m}}\}$. The soft boundary conditions $\partial \mathbf{u}{\text{/}}\partial x = 0$ are imposed on the outlet boundary$\{ x = {{X}_{m}}\}$. The aim of study is to investigate the behavior of the jet in the initial section of length of the order of 20R; to eliminate the influence of artificial outlet conditions on the calculation results in the computational domain, its length X_m is taken to be significantly greater than this size.

To solve numerically the problem we employ the universal method of solving the Navier–Stokes equations [9] in which the finite-difference method of spatial discretization in the directions x and r and semi-implicit scheme of integration in time are used. The uniform computational grid is used in the longitudinal direction and the non-uniform grid with exponential increase in the grid step at $r > R$ is used in the radial direction. The trigonometric Fourier series are used for representation of unknown functions over the angular coordinate. In varying the grid parameters (the dimensions X_m and R_m of the computational domain and the number of grid nodes Im and Jm in the corresponding directions), it was established that the set which is sufficient for satisfactory accuracy of calculations at the Reynolds number considered is ${{X}_{m}} = 40R$, ${{R}_{m}} = 6R$, $Im = 1024$, and $Jm = 128$. The majority of the results given below were obtained with these values of the parameters.

2 MAIN FLOW AND ITS STABILITY

In the present study we will give the results of investigations that correspond to the experimental conditions [4, 7, 8] at Re = 2850 (in the above-mentioned studies the Reynolds number is calculated on the base of the nozzle diameter but not on the base of the nozzle radius; therefore, it takes twice values). The profile of the longitudinal velocity component at the nozzle exit ${{U}_{0}}(r)$, that is implemented at this Re, takes the form reproduced in Fig. 1. In this figure we have also plotted the profile of vorticity ${{\Omega }_{0}}(r) = - d{{U}_{0}}{\text{/}}dr$. In what follows, all the quantities will be given in dimensionless form; the bulk velocity ${{U}_{b}}$ is taken as the velocity scale and the nozzle radius $R$ is taken as the length scale. The characteristic feature of the jet considered is the presence of three points of inflection in the velocity profile ${{U}_{0}}(r)$ (these points correspond to three local extrema in the vorticity distribution ${{\Omega }_{0}}(r)$). The first inflection point is located in the neighborhood of $r = 0.5$ and the other two are located in the neighborhood of $r = 0.8$. As shown below, such a velocity profile corresponds to two modes of unstable disturbances that develop in accordance with significantly different laws.

Fig. 1.

Velocity and vorticity profiles ${{U}_{0}}(r)$ and ${{\Omega }_{0}}(r)$ of the jet (a, b) in the nozzle exit section at $\operatorname{Re} = 2850$.

In order to calculate the main flow $\mathbf{u} = \mathbf{U} = (U(x,r),V(x,r),0)$ equations (1.1) are solved with the time-independent condition at inlet $\mathbf{u}(x = 0) = ({{U}_{0}}(r),0,0)$ and the initial condition $\mathbf{u}(x > 0)$ = u(x = 0). The problem is integrated in time up to establishment of a steady-state solution. In Fig. 2 we have reproduced the profiles of the longitudinal and radial velocity components $U(x,r)$ and $V(x,r)$ of main flow at various distances x from the nozzle exit section. At the Reynolds number considered, the velocity on the axis of jet varies only slightly, at x = 40 the drop is nothing more than approximately 1%. The main deformation of the profile of longitudinal velocity component is observed in the peripheral domain $r > 0.85$. The outer inflection points observed in the inlet flow disappear already at $x \approx 7.5$. The corresponding generalized inflection points determined from the condition $(U'(r){\text{/}}r)' = 0$ (here, prime denotes the derivative) and responsible for the development of instability in axisymmetric flows [4] disappear even earlier at $x \approx 3.75$. Along the entire jet the radial velocity component remains smaller than the longitudinal velocity component by three orders of magnitude. In each cross-section $x$ the radial velocity is positive in the region of jet core r < 1. This reflects the fact of jet expansion. In the external region the radial component is negative. This corresponds to entrainment of fluid from the surrounding space. This effect is maximum in the neighborhood of the inlet cross-section and weakens with growth in the distance from it.

Fig. 2.

Profiles of the longitudinal and radial velocity components (a, b) of main flow at various distances from the nozzle exit section.

In investigating the stability of flow, the velocity field in (1.1) can be represented in form of the sum of the main flow and a perturbation: $\mathbf{u} = \mathbf{U} + \mathbf{u}'$. The perturbations are assumed to be small and the equations are linearized with respect to ${\mathbf{u}}'$. The linear equations thus obtained were solved in two formulations. In the first, quasi-parallel, formulation variation in the main flow along the x direction is taken into account only parametrically. In other words, the equations are solved for a series of main flows of the form $\mathbf{U} = \mathbf{U}(r)$ obtained for various values of the coordinate x, while the terms that contain the derivatives of the velocity components of main flow with respect to x are neglected. Justification of using the quasi-parallel approach is the low rate of variation in the main flow along the longitudinal coordinate as compared with variation along the radius. In the second, more complete, formulation, called spatial in what follows, the linearized equations for perturbations are solved without additional simplifications with certain time-dependent boundary conditions at the inlet. In this case, the fact of stability or instability of main flow is established on the base of the character of evolution of various perturbations downstream.

Within the framework of the quasi-parallel approach, the solution of the stability problem reduces to solving linear equations whose coefficients are independent of both longitudinal and angular coordinates, as well as of time. The solutions of such equations can be sought in the form of normal modes, i.e., with the exponential dependence on these variables:

$$\mathbf{u}'(t,x,r,\theta ) = {\mathbf{v}}'(r)\exp [i(\alpha x + n\theta - \omega t)]{\kern 1pt} .$$

(2.1)

Here, $n$ is the integer azimuthal number and α and ω are the complex wavenumber and frequency. In this case the problem reduces to solution of the eigenvalue problem ${\mathbf{Lv}}' = i\omega {\mathbf{v}}'$ for a certain linear differential operator L that depends on the parameters α and n. After discretization of these equations in r, we obtain the eigenvalue problem for the complex matrix

$$\mathbf{A}(\alpha ,n){\mathbf{v}}'(r) = i\omega {\mathbf{v}}'(r).$$

(2.2)

In this case the vector ${\mathbf{v}}'(r)$ represents a finite-dimension vector of the values of the perturbation velocity components at nodes of the computational grid along the radial coordinate.

In accordance with the sense of the physical formulation of problem, for each n it is necessary to find the complex eigenvalues α as functions of the real frequency ω. However, the matrix A in (2.2) depends nonlinearly on α, so that it is difficult to determine α directly for a given ω. For this purpose, we have developed an iteration algoritm based on Newton’s method. In the first stage of the algoritm, all (complex) eigenvalues ω and the eigenvectors ${\mathbf{v}}'(r)$ of the problem (2.2) are determined for a certain real α with the use of the QR-algoritm. A solution corresponding to a perturbation growing with time, i.e., the eigenvalue ω with positive imaginary part ${{\omega }_{i}}$ and the corresponding eigenvector, is selected from them. These values are used as the initial approximation for iterations on the parameter towards decrease in ω_i for real α. Thus, we find a solution with the real frequency ω and the real wavenumber α, i.e., the eigensolution of the problem (2.2) that has the neutral behavior both in time and space. In the next stage, the neutral perturbation obtained is used as the initial approximation for determination of eigensolutions that grow in space at x > 0, i.e., the solutions corresponding to the real ω and complex α which have negative imaginary part α_i.

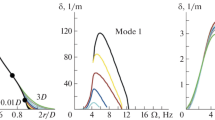
Among the axisymmetric solutions (n = 0), two modes of growing perturbations are found. One of them which is connected with the inflection point observed in the neighborhood of $r = 0.5$ in the velocity profiles, we will call it the inner mode, as distinct from the outer mode associated with the inflection points in the neighborhood of the outer jet boundary. In Fig. 3 we have plotted the growth rates $\sigma = - {{\alpha }_{i}}$ of each of the modes as functions of the real frequency $\omega$ at various distances from the nozzle exit section. With increase in x its maximum growth rate somewhat decreases from $\sigma \approx 0.21$ at x = 0 to $\sigma \approx 0.13$ at x = 20. The corresponding phase velocity remains almost constant: ${{c}_{r}} = 1.75$. This coincides approximately with the main flow velocity at the inner inflection points at various x. The frequency that corresponds to the maximally growing perturbation also somewhat decreases from $\omega \approx 3.0$ at x = 0 to $\omega \approx 2.5$ at x = 20.

Fig. 3.

Growth rates $\sigma$ of small perturbations with the azimuthal number n = 0 as functions of the frequency $\omega$ obtained within the framework of the quasi-parallel approach at various distances x downstream. Inner mode (a) and outer mode (b).

Perturbations of the outer mode (Fig. 3b) grow significantly more rapidly; however, their growth domain is restricted downstream by the interval $x < 3.2$. At the greater distances from the nozzle, the outer (generalized) inflection points in the velocity profile disappear and the related unstable mode also disappears. It is of interest that the curve $\sigma (\omega )$ is not continuous at the nozzle exit section and in the immediate neighborhood of it to $x \approx 0.1$, but is consists of two branches (curves (1) and (2) at x = 0 in Fig. 3b). In [10] such a behavior of the dependence $\sigma (\omega )$ was explaned. It was shown that the discontinuous $\sigma (\omega )$ corresponds to the absolute character of instability of flow. The perturbation growth rate of the outer mode reaches $\sigma \approx 4.9$ at x = 0. The maximum $\sigma$ decreases rapidly with increase in $x$. The corresponding frequencies also decrease from $\omega \approx 2.9$ at x = 0 to $\omega \approx 2.3$ at x = 3.2, and the phase velocity increases from ${{c}_{r}} \approx 0.44$ to ${{c}_{r}} \approx 0.75$.

In Fig. 4 we can see the interaction between the outer and inner modes in the range $1.25 < x < 2.5$ and $\omega < 1.25$. This interaction is similar to that revealed in [4] when the Reynolds number varies (see Fig. 26b in [4]). As distinct from the case n = 0 at small x, at n = 1 this interaction does not lead to absolute instability since it involves two modes which travel downstream.

Fig. 4.

Growth rates $\sigma$ of small perturbations with the azimuthal number n = 1 as functions of the frequency $\omega$ obtained within the framework of the quasi-parallel approach at various distances x downstream. Inner mode (a) and outer mode (b).

One more perceptible difference between growing perturbations of the outer and inner modes relates to the corresponding wave lengths. For the perturbations with the maximum growth of the inner mode, with increase in x the wavenumbers ${{\alpha }_{r}}$ decrease from 1.7 at x = 0 to 1.4 at x = 20. Similar perturbations of the outer mode turn out to be shorter by 3–4 times, their wavenumbers vary from 6.7 to 3.1 on the interval of $x$ from 0 to 3.13.

Among the three-dimensional growing perturbations corresponding to the azimuthal number n = 1, the inner and outer modes can be also distinguished (Fig. 4). Similarly to the case of axisymmetric perturbations, three-dimensional growing perturbations of the outer mode possess the growth rates which are higher by an order of magnitude as compared with the perturbations of the inner mode at small x; however, they grow only on a bounded interval $x < 3.2$. Growing perturbations of the inner mode exist over the entire jet length considered. We can also note that, as in the axisymmetric case, the growing perturbations of the outer mode have the wavelength by 3–4 times shorter than perturbations of the inner mode. As distinct from the axisymmetric case, at n = 1, in addition to those shown in Fig. 4, there are still several branches of growing perturbations which have insignificant ($\sigma < 0.05$) growth rates.

The eigenfunctions that correspond to the inner and outer mode perturbations have significantly different shapes. In Fig. 5 we have reproduced the profiles of absolute value of the longitudinal component $\left| {u(r)} \right|$ of the eigenfunctions that correspond to the frequency $\omega = 3.0$, similar to the frequency of most growing perturbations at $x = 0$. All the functions are normalized on the base of the condition $\max \left| {u(r)} \right|$ = 1. At $n = 0$ and $n = 1$ the eigenfunctions of the outer mode have similar structures with localization of perturbations in the neighborhood of outer inflection points at $r \approx 0.9$, in which $\left| {u(r)} \right|$ has the maximum gradient and two surrounding sharp peaks. The similarity of distributions at $n = 0$ and $n = 1$ testifies that at $n = 1$ and at such large distances from the axis of symmetry the variations in eigenfunctions over the angle are insignificant. On the contrary, at $n = 0$ and $n = 1$ the inner eigenfunctions have strongly different shapes. In the axisymmetric perturbation the velocity oscillations are predominant on the jet axis, while in the three-dimensional perturbation the velocity oscillations are predominant in the neighborhood of the inflection point at $r \approx 0.5$. The effect of the inner inflection point on the axisymmetric perturbation reduces to small irregularity in the distribution of $\left| {u(r)} \right|$ in the neighborhood of this point. Of interest that the effect of the outer inflection point in form of considerable peaks in the $\left| {u(r)} \right|$ profiles for the inner mode is expressed much more clearly for both axisymmetric and three-dimensional perturbations. These peaks in the eigenfunction profiles disappear at large x with disappearance of outer inflection points.

Fig. 5.

Profiles of absolute value of the longitudinal component |u(r)| of the eigenfunction of perturbation at $x = 0$ and $\omega = 3.0$ on the interval $r \in [0,\;2]$. Red and green curves correspond to perturbations of the inner and outer mode, respectively. Axisymmetric perturbations (a) and three-dimensional (n = 1) perturbations (b).

3 SPATIAL DEVELOPMENT OF SMALL PERTURBATIONS

In investigating the spatial development of small perturbations, the velocity field can be represented in form of the sum of main steady-state flow $\mathbf{U} = (U(x,r),V(x,r),0)$ and a perturbation $\mathbf{u}'(t,x,r,\theta )$. The Navier–Stokes equations linearized with respect to perturbations are integrated in time with zero initial conditions and the boundary conditions at inlet in the form:

$$\mathbf{u}'(t,0,r,\theta ) = a(t)\operatorname{Re} \{ {\mathbf{v}}'(r)\exp [i(n\theta - \omega t)]\} ,\quad a(t) = \left\{ \begin{gathered} \sin \frac{{\pi t}}{{2{{t}_{0}}}},\quad t < {{t}_{0}} \hfill \\ 1,\quad t \geqslant {{t}_{0}}. \hfill \\ \end{gathered} \right.$$

(3.1)

Here, ${\mathbf{v}}'(r)$ is the eigenvector of the problem (2.2) at given azimuthal number n and frequency ω and Re{…} denotes the real part of a complex quantity. The amplitude factor $a(t)$ ensures continuous variation in the inlet perturbation amplitude from zero at t = 0 (this is in agreement with zero initial conditions at all $x$) to unity at $t = {{t}_{0}}$ ~ 1. As normalization of the eigenvector, we take the condition

$$\int\limits_0^{{{R}_{m}}} {{{{\left| {{\mathbf{v}}'(r)} \right|}}^{2}}} rdr = 1.$$

(3.2)

The perturbation propagates with time from the inlet cross-section over the entire length of the computational domain. The calculation is continued to tending of the solution to the periodic behavior with the frequency $\omega$ given in the inlet cross-section for all x. After this, in parallel with integration in time, the average-over-oscillation period quantities are calculated as functions of the longitudinal coordinate. In Fig. 6 we have plotted the graphs of variation of the average integral amplitude $A(x)$ of axisymmetric and three-dimensional (n = 1) perturbations along the coordinate x; these graphs are obtained with the inlet conditions that correspond to the inner and outer eigenmodes at the frequency $\omega = 3.0$. The amplitude $A(x)$ is determined from the formula

$${{A}^{2}}(x) = \frac{1}{{\pi T}}\int\limits_0^{{{R}_{m}}} r dr\int\limits_0^T d t\int\limits_0^{2\pi } {{{{\left| {\mathbf{u}'(t,x,r,\theta )} \right|}}^{2}}} d\theta .$$

(3.3)

Fig. 6.

Evolution of the integral perturbation amplitude (3.3) at the frequency $\omega = 3.0$ at n = 0 (a) and 1 (b). Red and green curves correspond to perturbations of the inner and outer mode, respectively.

As the averaging period in time T, we take the interval multiple to the oscillation period $2\pi {\text{/}}\omega$. Variation in $A(x)$ is absolutely identical for axisymmetric and three-diemnsional perturbations. After several small oscillations on the initial interval, the amplitude of the inner mode tends to the monotonic growth regime which continues to the end of the computational domain. Growth of perturbations of the inner mode is in agreement with the fact of instability of the velocity profiles of main flow with respect to such perturbations at all $x \leqslant {{X}_{m}}$, obtained within the framework of the quasi-parallel approach.

The perturbations of the outer mode develop quite different. The initial rapid growth of the amplitude ends at $x \approx 2.5$; thereafter, there follows a damping section in which the amplitude decreases by two orders of magnitude. Beyond this initial section of development, the perturbations again begin to grow but already in accordance with the law of growth on the inner mode. The initial evolution of the outer mode is also in agreement with prediction of the results of the quasi-parallel approach. On the initial interval x the growth rate of such perturbations is significantly greater that the similar quantity for perturbations of the inner mode; however, already at $x > 2.5$ the perturbations of the outer mode damp at $\omega = 3.0$; the decrease in $A(x)$ in Fig. 6 at $x > 2.5$ relates to this fact. The perturbation growth similar to growth of the inner mode at large x shows that the component that corresponds to the most rapidly growing inner mode can be distinguished in the perturbation against the background of general damping.

Approximating the curve $A(x)$ at each point x by an exponential function, we can estimate the local perturbation growth rate as follows:

$${{\sigma }_{p}}(x) = \frac{{d\ln A(x)}}{{d{\kern 1pt} x}} \equiv \frac{1}{A}\frac{{dA(x)}}{{dx}}.$$

(3.4)

In Fig. 7 we have given the estimates of the growth rate thus obtained and calculated for perturbations of the inner mode beyond the initial section of development at various values of the frequency ω at n = 0 and n = 1. At $x \leqslant 20$ these dependences are qualitatively and quantitatively similar to the analogous graphs $\sigma (\omega )$ obtained within the framework of the quasi-parallel approach (Figs. 3 and 4).

Fig. 7.

Local growth rates ${{\sigma }_{p}}$ of small perturbations with the azimuthal numbers n = 0 (a) and 1 (b) as functions of the frequency $\omega$ obtained within the framework of the spatial approach at various distances $x$ downstream.

In Fig. 8 we have compared the results of the quasi-parallel and spatial approaches in more detail. In this figure we have reproduced the growth rate of axisymmetric peturbations of the inner mode as a function of ω for various x obtained within the framework of both approaches. In Fig. 9 we have performed similar comparisons for the growth rate of three-dimensional perturbations (n = 1). The qualitative correspondence of the results of two approaches is observed in all cases. The frequencies at which the maximum perturbation growth takes place coincide with high accuracy. The estimate of the perturbation growth rate obtained within the framework of the spatial approach for all ω is somewhat greater than the estimate within the quasi-parallel approach. At n = 0 the difference between the maximum values is equal to approximately 10% and at n = 1 to approximately 15%. The single prominent difference concerns the three-dimensional perturbations and consists in the slower decrease in ${{\sigma }_{p}}$ as compared with $\sigma$ for increase in $\omega > 2$. The possible cause of the increased growth rate of perturbations of ${{\sigma }_{p}}$ at n = 1 and $\omega > 2$ is the presence of several branches of growing perturbations of this type. This was revealed in using the quasi-parallel approach.

Fig. 8.

Growth rates of small perturbations with the azimuthal number n = 0 obtained within the framework of the spatial approach ${{\sigma }_{p}}$ (solid curves) and the quasi-parallel approach $\sigma$ (dashed curves): (a) $x = 12.5$, (b) $15.0$, (c) $17.5$, (d) $20.0$.

Fig. 9.

Growth rates of small perturbations with the azimuthal number n = 1 obtained within the framework of the spatial approach ${{\sigma }_{p}}$ (solid curves) and the quasi-parallel approach $\sigma$ (dashed curves): (a) $x = 12.5$, (b) $15.0$, (c) $17.5$, (d) $20.0$.

4 NONLINEAR INTERACTION OF PERTURBATIONS AND TURBULENCE TRANSITION

As in investigation of the spatial development of small perturbations, in the calculations of the nonlinear interaction between perturbations the velocity field can be represented in form of the sum of main steady-state flow U = (U(x, r), V(x, r), 0) and a perturbation u'(t, x, r, θ). The perturbations are seeked in the form of a finite Fourier series in the angular coordinate:

$${\mathbf{u}}'(t,x,r,\theta ) = \sum\limits_{n = 0}^{{{N}_{m}}} {\operatorname{Re} \{ {\mathbf{u}}_{n}^{'}(t,x,r)\exp (in\theta )\} } .$$

(4.1)

The nonlinear Navier–Stokes equations are integrated in time with zero initial conditions. The boundary conditions at inlet are specified similarly to (3.1) in the form:

$${\mathbf{u}}_{n}^{'}(t,0,r) = {{A}_{n}}(0)a(t){\mathbf{v}}_{n}^{'}(r)\exp ( - i\omega t).$$

(4.2)

Here, A_n(x) are the amplitudes of the corresponding harmonics and ${\mathbf{v}}_{n}^{'}$(r) are the eigenfunctions of the linear problem of stability of inlet flow. As in (3.1), a(t) is a transient function that ensures continuous variation in the amplitude of the corresponding inlet perturbation from zero at t = 0 to A_n(0) at t = t₀ ~ 1. The amplitude A_n(x) can be determined similarly to (3.3) by integrating in r and averaging of the quantity |${\mathbf{u}}_{n}^{'}$(t, x, r)|² in time.

The calculations were carried out starting from A_n(0) = 0 at n > 1, i.e., perturbations in the form of combinations of the zeroth and first angular harmonics with different amplitudes were given at inlet. In this case the higher harmonics develop at x > 0 as a result of nonlinear interactions between three-dimensional perturbations. When the amplitude A₁(0) of the inlet perturbation is given to be zero, the flow remains axisymmetric for all x. The number N_m of the harmonics which are taken into account varied from 1 to 32. It was found that both the qualitative and, in majority of cases, also the quantitative behavior of flow on the interval that precedes transition to the turbulent regime is satisfactorily reproduced already starting from N_m = 4. The majority of the results represented below were obtained at N_m = 8.

In [7] the experiments carried out on the facility in the Institute of Mechanics of Moscow State University were described in detail. In these experiments the development of a jet subject to artificial perturbations of axisymmetric form was studied. The perturbations were introduced at the distance x = 0.32 from the nozzle exit cross-section by means of thin rings located coaxially with the jet and oscillating in the axial direction. Two rings of different diameters which ensured excitation of the perturbations close to the outer and inner modes of linear stability were used. In excitation of the outer mode the length of laminar jet fragment is appreciably shortened over a certain ring oscillation frequency range as compared with the case of absence of perturbations (for ring at rest). The maximum reduction of the laminar fragment to approximately x = 5 is observed at the frequency that coincides with the maximum growing perturbation frequency predicted by the linear theory of stability. Recall that natural transition under the experimental conditions at the Reynolds number considered Re = 2850 takes place at x ≈ 12. The amplitude of the linear velocity of ring oscillations Δu' was maintained constant in varying the frequency, in dimensionless form this velocity is equal to ≈0.035. At n = 0, for normalization of perturbations (4.2) used in the present study, this corresponds to A_n(0) ≈ 10^–2.

For simulation of the nonlinear development of axisymmetric perturbations it is sufficient to restrict our attention to N_m = 0 in (4.1). The calculations were carried out over the frequency interval 1 ≤ ω ≤ 5 that coincides with the interval of maximum growing linear perturbations (see Fig. 3). In order to reproduce the experimental conditions the inlet perturbation amplitude A₀(0) was taken to be equal to 10^–2. It was revealed that at this amplitude the behavior of a perturbation of the outer mode in the initial fragment replicates qualitatively the spatial development of a small perturbation given in Fig. 6. By virtue of nonlinearity of the process, the quantitative characteristic values somewhat change. For example, at ω = 3 the initial rapid growth of perturbation amplitude is stopped already at x ~ 1: during this time the amplitude grows only by 1.8 times, whereas in the linear development the perturbation amplitude in the initial section increase by an order of magnitude. Thereafter, there follows the stage of decrease in the amplitude and restructuring of the perturbation into a perturbation of the inner mode. Then the perturbation of the inner mode strengthens almost linearly to reaching A(x) ≈ 0.03 at x = 25, saturation occurs, and a stage of certain relaxation (slow decrease in the amplitude) to A ≈ 0.02 at x = 40 takes place. At all points of jet up to the exit cross-section the velocity oscillations remain regular with minimum deviation from the harmonic law.

Increase in the initial amplitude by an order of magnitude A₀(0) = 10^–1 does not change the qualitative behavior of flow except for certain details. The perturbation begins to damp at once at x > 0 by-passing the interval of initial growth. After this, as in the case of lower initial amplitude, the perturbation goes over into a perturbation of the inner mode, somewhat strengthens (in this case to A₀ ≈ 0.09 already at x ≈ 8), and goes over into the relaxation stage. The time behavior of perturbations also remains similar to the harmonic behavior.

When the perturbations of the inner mode are excited in the inlet cross-section, the process is simplified due to the absence of the stage of restructuring of the perturbation of outer mode into inner mode. All other is qualitatively conserved: at the lower initial amplitude A₀(0) = 10^–2 the perturbation grows similarly to the linear growth in Fig. 6, reaches a maximum, and relaxes to A(40) ≈ 0.04; at A₀(0) = 10^–1, after a minimum initial growth, at once the stage of slow damping to A(40) ≈ 0.09 occurs.

The results obtained of the development of axisymmetric perturbations contradict the experiment [7]. In the calculations it was shown that the development of axisymmetric perturbations leads to establishment of regular oscillations, whereas in the experiments not only the fact of turbulence transition but also reduction in the length of laminar section under the action of an artificial axisymmetric perturbation was established. Such a difference is attributable to the fact that under the experimental conditions, in addition to artificial perturbation, there are three-dimensional perturbations of the uncontrollable nature, whose development just leads to accelerated transition against the background of artificial axisymmetric perturbation. The fact that turbulence transition takes place in the absence of artificial perturbations in the jet and, consequently, some uncontrollable perturbations are present in the jet also testifies in favor of this assumption.

For studying the possibility of appearance of turbulence transition under the action of three-dimensional perturbations we carried out calculations of the nonlinear evolution of initially fairly small perturbations, A_n(0) = 10^–3 at n = 0 and 1. Individually, we considered the cases of perturbations which correspond to the inner and outer modes of stability. The inlet perturbations corresponded to the frequency ω = 3. This is close to the frequency of maximally growing perturbations in the initial jet section (see Figs. 3 and 4). In this case the perturbations of the inner mode on the interval 0 < x < 20 grow in accordance with the linear law of development of small perturbations (Fig. 6) and almost do not interact with each other. The axisymmetric perturbation grows by approximately 30 times and the three-dimensional perturbation by approximately 20 times. Starting from x = 20, growth of the amplitude of the first angular harmonic (n = 1) accelerates, probably, under the action of the zeroth harmonic that appreciably grew to this instant. The opposite effect of the first harmonic on the zeroth harmonic is quadratic; therefore, it is manifested somewhat later, when A₁ reaches ~10^–1. This longitudinal occurs approximately at x = 25. The perturbations with the higher azimuthal numbers, that develop by virtue of nonlinearity, rapidly grow at x > 0 and at x ≈ 25 they have approximately the same amplitudes (in order of magnitude) as the perturbations corresponding to n = 0 and n = 1. At this instant, irregular high-amplitude fluctuations appear in the velocity oscillations considered as functions of time and coordinate. This fact can be qualified as turbulence transition. In Fig. 10a we have reproduced variation in the longitudinal component of the perturbation velocity u'(x) along the longitudinal coordinate at r = 0.5 and θ = 0 at a certain fixed instant of time. The graph is bounded by the coordinate x = 30 at which the irregular oscillations of considerable amplitude are already formed.

Fig. 10.

Variation in the longitudinal velocity component of the perturbation $u'(x)$ along the longitudinal coordinate at $r = 0.5$, $\theta = 0$ at a certain fixed instant of time. Inlet perturbations of the inner mode (a) and the outer mode (b) at the frequency $\omega = 3$ and the initial amplitudes ${{A}_{0}}(0) = {{10}^{{ - 3}}}$ and ${{A}_{1}}(0) = {{10}^{{ - 3}}}$.

In Figs. 11a and 11b we have shown flow visualization. In the first figure we have reproduced the instantaneous field of the angular component of vorticity ω_θ = ∂${v}$/∂x – ∂u/∂r (u, ${v}$, and w are the components of the velocity vector u that correspond to the axial, radial, and azimuthal coordinates of the cylindrical coordinate system) in the plane (x, r' ≥ 0, θ = 0) and the field –ω_θ in the plane (x, r' < 0, θ = π). Here, r' = r at r' > 0 and r' = –r at r' < 0. In such a representation the continuity and the smoothness of the represented field are conserved across line r' = 0. This visualization clearly demonstrates the beginning of turbulence transition at x ~ 25 when clearly expressed irregular fine-scale component appears in the vorticity field. At x > 25 the used spatial resolution in the angular coordinate (4.1) becomes insufficient at N_m = 8. It was tested that increase to N_m = 32 in the number of harmonics taken into account does not change qualitatively the flow pattern in the transition stage, i.e., at x < 25. Thus, we can hope that the transition stage is correctly reproduced in calculation. In Fig. 11b we have reproduced the vorticity field of the perturbation $\omega _{\theta }^{'}$ = ∂${v}$'/∂x – ∂u'/∂r in the plane (x, r, θ = 0) which gives a certain additional representation on the character of development of perturbation in the transition stage. Note that the geometric flow proportions are conserved in Fig. 11a, while in Fig. 11b the image is horizontally extended. We can see that along the entire jet the perturbations are concentrated along the line r ≈ 0.5, i.e., in the region of the inner inflection point in the main flow velocity profile. The perturbation wavelength λ_x ≈ 4 is also conserved approximately constant.

Fig. 11.

Field of the angular component of vorticity ${{\omega }_{\theta }}$ (a, c) and perturbatiom of vorticity $\omega _{\theta }^{'}$ (b, d). Inlet perturbations of the inner mode (a, b) and the outer mode (c, d) at the frequency $\omega = 3$ and the initial amplitudes ${{A}_{0}}(0) = {{10}^{{ - 3}}}$ and ${{A}_{1}}(0) = {{10}^{{ - 3}}}$.

In the initial stage the evolution of perturbations of the outer mode of stability also corresponds to the linear behavior (Fig. 6). The amplitudes of both harmonics n = 0 and 1 increase by approximately an order of magnitudes on the interval x < 2. Then A₁(x) varies in another way as compared with the linear case. The effect of the increased axisymmetric perturbation component leads to more rapid growth of three-dimensional components. This relates not only to the perturbation at n = 1, which continues to grow, but also to perturbations of the higher harmonics whose initial amplitudes were equal to zero. The amplitude of axisymmetric perturbation decreases at x > 2, but not by two orders of magnitude, as in the linear case, but by less than an order of magnitude. Starting from x ≈ 5, A₀(x) also begins to grow. Already at x ≈ 12 powerful irregular fluctuations appear in the velocity oscillations (Fig. 10b), i.e., the turbulent flow regime is established. The vorticity field shown in Figs. 11c and 11d demonstrates jet modification in the transition section. The perturbation applied to the outer jet region r ≈ 0.85 is gradually displaced towards r = 0.5 in evolution downstream. The characteristic perturbation wavelength increases from λ_х ≈ 1 at inlet to λ_х ≈ 2 already at x = 10.

The calculations performed show that natural turbulence transition observed experimentally at x ≈ 12 is attributable to the presence of uncontrollable three-dimensional perturbations with the amplitude A_n ~ 10^–3. In this case, probably, transition is initiated by the development of perturbations of the outer mode of linear stability. We can also assume that reduction in the length of transition region in applying artificial axisymmetric perturbations with the amplitude ~10^–2, observed in the experiment [6, 7], is initiated not so much by the development of the axisymmetric perturbations themselves, as by their influence on the growth rate of background three-dimensional perturbations. The fact mentioned above that the growth of three-dimensional low-amplitude perturbations strengthens against the background of the axisymmetric perturbation when the perturbation amplitude reaches the value of the order of 10^–2 testifies in favor of this fact.

To verify this hypothesis, we carried out a series of numerical experiments in which the initial amplitudes of perturbations of the outer mode were given in the form A₀(0) = 10^–2 and A₁(0) = 10^–3.. In this case the perturbation frequencies of both harmonics coincided and varied over the range 1 ≤ ω ≤ 5. Such conditions can approximately correspond to the experimental conditions [6, 7] under the assumption that a less intensive three-dimensional perturbation is applied to flow at the same frequency together with the artificial axisymmetric perturbation. For example, this perturbation can result due to the non-ideal device for generation of artificial perturbations. In Fig. 12 we have reproduced visualization of the flows obtained at various frequencies of applied perturbations. In the same figure we have given a photo of smoke visualization of the jet obtained in the experiment [6]. Both in the calculation and in the experiment we can observe the dependence of the length of transition region on the frequency of the perturbation applied. In both cases turbulence develops most rapidly at the frequencies ω ≈ 2.5–3.0. In accordance with the linear theory, the maximum perturbation growth is observed in this frequency range.

Fig. 12.

Upper row: visualization of calculations (field of the angular component of vorticity): (a) $\omega = 1$, (b) 2, (c) 2.5, (d) 3, (e) 3.5, (f) 4, and (g) 5. Lower row: smoke visualization of the experiment: (a) $\omega = 0$, (b) 1.7, (c) 2.0, (d) 2.3, (e) 2.6, (f) 2.7, (g) 2.9, (h) 3.1, (i) 3.3, (j) 3.6, (k) 3.7, and (l) 6.9.

In the experiments it is obvious that there are three-dimensional perturbations in the neighborhood of transition zone (Fig. 12), the artificially applied perturbations being similar to axisymmetric ones. This fact is in agreement with the conclusion on necessity of initial small three-dimensional perturbations which, growing rapidly due to nonlinear interaction, lead finally to appearance of flow turbulence. The role of axisymmetric perturbations in such a mechanism consists not in the fact of their growth and thus to jet self-turbulization, but in ensuring the nonlinear growth of three-dimensional perturbations which just lead to the development of flow turbulence.

Conspicuous is the fact that at ω = 3 and the perturbation amplitudes A₀(0) = 10^–2 and A₁(0) = 10^–3 the length of transition zone reduces only slightly as compared with the variant A₀(0) = 10^–3 and A₁(0) = 10^–3 described above (Figs. 11c and 11d). This can be attributable to the fact that the quantity A₀ = 10^–2 is close to the limit of the linear growth of the axisymmetric perturbation in the initial section of jet. As noted above in describing the development of axisymmetric perturbations, at A₀(0) = 10^–2 the zeroth harmonic grows only by 1.8 times in the initial section, whereas at A₀(0) = 10^–3 it grows almost by an order. Correspondingly, in these two cases the effect of axisymmetric perturbation on the growth of three-dimensional perturbation is similar. Note that such an influence on the evolution of small three-dimensional perturbations is of importance. If we refuse the axisymmetric component in the inlet perturbation (A₀(0) = 0 and A₁(0) = 10^–3), then during long time the growth of three-dimensional perturbations remains almost linear and, as a result, the length of the transition domain increases almost to x = 30.

It should be also noted that the character of flow development strongly depends on the initial amplitude of three-dimensional perturbations. In all the variants described above, small initial perturbations A₁(0) ≤ 10^–3 were considered. Even in the absence of the axisymmetric component, increase in this level leads to more rapid switching-on of nonlinear mechanisms and, as a result, reduction in the length of transition region. In Fig. 13 we have reproduced flow visualization similar to that in Fig. 11. This flow was obtained with a purely three-dimensional inlet perturbation but of increased amplitude: A₀(0) = 0 and A₁(0) = 10^–2 (the initial section of the development of jet is shown). In this case the perturbations grow very rapidly, partly owing to early excitation of the higher angular harmonics. Appearance of turbulence that is accompanied by the development of irregular oscillations takes place already at x ≈ 4. This result is in agreement with the experimental data on rapid transition in the jet subject to artificial three-dimensional perturbations that correspond to n = 1. As shown in [8], in this case the length of transition region reduces to 1–2 jet diameters.

Fig. 13.

Field of the angular component of vorticity ${{\omega }_{\theta }}$ (a) and perturbatiom of vorticity $\omega _{\theta }^{'}$ (b). Inlet perturbations of the outer mode at the frequency $\omega = 3$ and the initial amplitudes ${{A}_{0}}(0) = 0$ and ${{A}_{1}}(0) = {{10}^{{ - 2}}}$.

SUMMARY

The results of numerical simulation of stability and nonlinear evolution of perturbations in the round jet are given. The conditions of the laboratory experiment carried out earlier at Re = 2850 in the Institute of Mechanics of Moscow State University are reproduced [4–8]. The characteristic feature of the jet under consideration is the presence of three inflection points in the inlet velocity profile. This fact determines significantly the properties of the flow. Linear stability is investigated with the use of two approaches: quasi-parallel and spatial. In the first approach, modification of main flow along the stream is taken into account parametrically: the problem of stability is solved for a series of the main flow profiles that correspond to various distances from the inlet. In the spatial approach the linearized Navier–Stokes equations for perturbations are integrated with regard to modification of main flow. Good quantitative agreement of the results of two approaches, as well as the agreement with the results of inviscid theory [4, 7], is obtained. The basic qualitative property of flow stability consists in existence of two modes of growing perturbations, namely, the inner and outer modes which correspond to the inner ($r \approx 0.5$) and the pair of outer ($r \approx 0.85$) inflection points. The growth rate of the outer mode perturbations is greater by an order of magnitude than the similar growth rate of the inner mode perturbations. However, this instability disappears already in the earlier stages of the jet development together with disappearance of the outer inflection points in the main flow velocity profile. Instability to the inner modes is conserved along the entire distance of the jet development.

The numerical calculations were carried out with the aim to explain and interpret the results of the laboratory experiment [7] in which it was revealed that the length of the turbulence transition zone in the jet subject to time-periodic axisymmetric perturbations changes. In the calculations it was shown that the axisymmetric perturbations, even of considerable initial amplitude, do not lead to turbulence transition. The oscillations initiated by the development of such perturbations conserve the regular character, close to harmonic one. Turbulence transition observed in the experiment can be attributable to the presence of uncontrollable three-dimensional perturbations that are strengthened against the background of fairly intensive artificial perturbations. The present investigations confirm this hypothesis. Inlet perturbations in form of combination of axisymmetric and small three-dimensional perturbations lead to the development of turbulence at a distance of approximately five jet diameters. As in the experiment, the length of transition region reduces when the inlet perturbation frequency is close to the frequency of most rapidly growing perturbations from the linear theory.

The three-dimensional perturbations initiate transition in the described pattern, while axisymmetric perturbations of fairly high amplitude only accelerate their growth. Hence it follows that more intense initial three-dimensional perturbations can ensure more rapid transition even in the absence of the axisymmetric component. The last assumption is confirmed by calculations with the initial three-dimensional perturbations of finite amplitude. In this case the length of transition zone reduces to 1–2 jet diameters. This explains the cause of rapid transition obtained in experiments [8].