The problem of stability of the boundary layer with diffuse combustion was the stimulating problem for the present study. At the first time, the problem of diffuse flame in the boundary layer was formulated by Emmons [1]. The investigations of the boundary layer with diffuse combustion were carried out many times. This is reflected in review [2].

The problem of stability of the boundary layer with chemical reactions is studied in the lesser extent. A review of the corresponding studies carried out to the end of  1970th can be found in monograph [3]. However, almost all studies cited in the review relate to the problem of gravitational convection. Studies [4–6] relate to the present theme in the highest extent. In [4] the analysis is restricted to the inviscid approximation, i.e., in the stability equations the terms that contain the coefficients of molecular mass, momentum and energy transfer are neglected. In [3, 5, 6] the investigations were carried out both in the inviscid approximation and with regard to the mass, momentum and energy transfer coefficients in the Dan–Lin approximation [7]. In these papers stability was studied under the conditions of oxygen and nitrogen dissociation and recombination. Similar investigations were also carried in the more general formulation for the hypersonic boundary layer; the detailed information on these studies can be found in [8, 9]. However, these investigations considered only the stability of flow with respect to two-dimensional disturbances for which the direction of the wave vector coincides with the direction of main flow.

The initial investigations of stability of laminar flows in the presence of diffuse flame were carried out for fuel and oxidant mixing layers or for supply of fuel jet in the oxidizing agent and the problem was solved by neglecting viscosity in the stability equations. The detailed information on such studies can be found in review [10]. In this connection, it is noteworthy to mention study [11]. Evidently, in that study stability of a jet in the presence of flame was first considered with regard to viscosity and thermal conductivity in the stability equations. To present, there are no investigations of stability of the boundary layer in burning the fuel that is supplied through a permeable surface and burns in the oxidant stream.

The presence of diffuse flame leads to internal heat release and change in composition of the mixture, while the density depends on both the temperature and the composition of mixture (its molecular mass). Therefore, stability of the boundary layer with combustion depends on the Mach number, the temperature boundary conditions, mixing of foreign gases and the condition of heat supply inside the boundary layer. However, in many cases, for example, in burning hydrocarbon fuels in air stream, the gas density depends mainly on the temperature. The molecular mass of mixture varies only slightly along the boundary layer [12] and its variation can be neglected. In supplying fuel through the porous wall which is located in the oxidant stream, an important factor that affects stability of the boundary layer relates to gas injection.

An important result of [3, 5] consists in the fact that the terms in the stability equations related to disturbances of heat source and concentrations of substances are inversely proportional to the Reynolds number and they are of the same order as the terms that take into account the flow non-parallelism. In these studies it was shown that stability of the boundary layer considered in the approximation of local flow parallelism depends on only the density and velocity distributions in main flow. From this fact it follows that the influence of perturbations of the concentration source and the temperature on stabilities of the boundary layers is comparable with the influence of non-parallelism of main flow. The slight influence of perturbations of the heat source on stability of the boundary layer without blowing was confirmed in [13]. Therefore, these perturbations can be neglected in investigating the stability of boundary layers in the parallel flow approximation. In addition, this is in agreement with the theory of stability of diffuse flame at large Damkohler numbers Da (the flame zone is much less than the boundary layer thickness) [14] and the results [15] at finite Da. Thus, stability of diffuse flame in the boundary layer can be satisfactorily described by stability of homogeneous gas flow with energy supply inside the layer and gas injection through the porous wall.

Therefore, in the present study the temperature distribution under the diffuse flame conditions is simulated by means of a heat source and the density is simulated by means of the inverse proportionality to the temperature. The investigations are carried out for subsonic flow past a plate, the Mach number M ≪ 1.

1 MAIN FLOW IN THE BOUNDARY LAYER

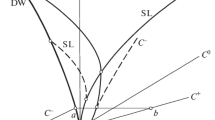
In Fig. 1 we have shown the boundary layer with the band of heat supply and gas injection through the porous wall.

Fig. 1.
figure 1

Diagram of the boundary layer with heat supply and gas injection through a porous wall.

Full size image

In dimensionless variables laminar homogeneous gas flow in the boundary layer can be described by the following system of equations [16]:

$$\begin{gathered} \frac{{\partial (u\rho )}}{{\partial x}} + \frac{{\partial ({v}\rho )}}{{\partial y}} = 0,\quad \rho \left( {u\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial y}}} \right) = \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right), \\ \rho \left( {u\frac{{\partial I}}{{\partial x}} + {v}\frac{{\partial I}}{{\partial y}}} \right) = \frac{\partial }{{\partial y}}\left[ {\frac{\mu }{{\Pr }}\frac{{\partial I}}{{\partial y}} + \mu \left( {1 - \frac{1}{{\Pr }}} \right)u\frac{{\partial u}}{{\partial y}}} \right] + \rho Q, \\ \end{gathered} $$
(1.1)
$$\rho = \frac{{pm}}{{RT}},\quad I = h + \frac{{{{u}^{2}}}}{2},\quad \mu = {{T}^{{3/2}}}\left( {1 + \frac{{{{T}_{s}}}}{{{{T}_{e}}}}} \right){{\left( {T + \frac{{{{T}_{s}}}}{{{{T}_{e}}}}} \right)}^{{ - 1}}}.$$

Here, u and \({v}\) are the projections of the velocity vector on the orthogonal coordinates x (parallel to the plate surface) and y (normal to the surface), respectively, ρ is the density, p is the pressure, T is the temperature, h = cpT is the enthalpy, Q is the heat introduced in the unit mass per unit time, m is the gas molecular weight, R is the universal gas constant, μ is the dynamic viscosity coefficient, cp is the specific heat capacity at constant pressure, and Pr is the Prandtl number. It is assumed that cp and Pr are constant and Ts = 110 K. The system (1.1) is nondimensionalized using the following scales: the length \({{{v}}_{e}}\)/ue, the viscosity μe, the velocity ue, the temperature Te, the density ρe, the enthalpy \(u_{e}^{2}\), the heat supply \(u_{e}^{4}{{\rho }_{e}}{\text{/}}{{\mu }_{e}}\), the specific heat capacity \(u_{e}^{2}{\text{/}}{{T}_{e}}\) and the universal gas constant, and the pressure \({{\rho }_{e}}u_{e}^{2}\). The subscript e denotes the parameters at the outer boundary layer edge.

On the plate surface (y = 0) u = 0, \({v}\) = j/ρw ( j is the mass flow rate through the wall), T = Tw, and u = T = 1 at the outer boundary layer edge.

In the local self-similar approximation the system can be reduced to the form:

$$\begin{gathered} \frac{d}{{dY}}\left( {C\frac{{{{d}^{2}}f}}{{d{{Y}^{2}}}}} \right) + \frac{f}{2}\frac{{{{d}^{2}}f}}{{d{{Y}^{2}}}} = 0, \\ \frac{d}{{dY}}\left( {\frac{C}{{\Pr }}\frac{{dg}}{{dY}}} \right) + \frac{f}{2}\frac{{dg}}{{dY}} = \frac{{u_{e}^{2}}}{{{{I}_{e}}}}\frac{d}{{dY}}\left[ {\left( {\frac{1}{{\Pr }} - 1} \right)C\frac{{df}}{{dY}}\frac{{{{d}^{2}}f}}{{d{{Y}^{2}}}}} \right] - Q\frac{{u_{e}^{2}}}{{{{I}_{e}}}}\operatorname{Re} _{b}^{2}{{\left( {\frac{{\operatorname{Re} }}{{{{{\operatorname{Re} }}_{b}}}}} \right)}^{2}}, \\ \end{gathered} $$
(1.2)
$$\frac{{df}}{{dY}} = u,\quad g = \frac{{u_{e}^{2}I}}{{{{I}_{e}}}},\quad dY = \rho \frac{{dy}}{{\operatorname{Re} }}{\text{,}}\quad C = \rho \mu ,\quad {\text{ Re}} = \sqrt x .$$

Here, Reb is the constant Reynolds number of a particular problem. The solution of system (1.2) depends on x (via Re) parametrically and must satisfy the boundary conditions

$$f = j\operatorname{Re} ,\quad \frac{{df}}{{dY}} = u = 0,\quad T = {{T}_{w}}(Y = {\text{ }}0);\quad u = g = 1\,\,(Y = \infty ).$$

The dependence of heat supply on the normal coordinate is taken in the form:

$$Q\frac{{u_{e}^{2}}}{{{{I}_{e}}}}\operatorname{Re} _{b}^{2} = Au(1 - u)\exp \left( { - {{{\left( {\frac{{y - {{y}_{f}}}}{{{{\Delta }_{f}}}}} \right)}}^{2}}} \right).$$

Here, the quantity Δf is proportional to the width of the heat supply band which is much less than the boundary layer thickness and yf  is the problem parameter that characterizes the location of the heat supply band. By virtue of the fact that in heat supply the main contribution is implemented in a narrow band, i.e., at \(y - {{y}_{f}} \ll 1\), we can restrict out attention to the first term of velocity expansion in the coordinate near yf, i.e., adopt \(\left( {u - {{u}_{f}}} \right) \approx {{\left( {du{\text{/}}dy} \right)}_{f}}(y - {{y}_{f}})\), where the subscript f denotes the flow parameters at \(y = {{y}_{f}}\). Then

$$y - {{y}_{f}} \approx \left( {u - {{u}_{f}}} \right)\left( {\frac{{du}}{{dy}}} \right)_{f}^{{ - 1}} = \left( {u - {{u}_{f}}} \right)\frac{{\operatorname{Re} }}{{{{\rho }_{f}}}}{{\left. {{{{\left( {\frac{{du}}{{dY}}} \right)}}^{{ - 1}}}} \right|}_{{Y = {{Y}_{f}}}}},$$
$$y - {{y}_{f}} \approx \left( {u - {{u}_{f}}} \right){{T}_{f}}({{\operatorname{Re} }_{b}})\frac{{{{T}_{f}}(\operatorname{Re} )}}{{{{T}_{f}}({{{\operatorname{Re} }}_{b}})}}{{\operatorname{Re} }_{b}}\frac{{\operatorname{Re} }}{{{{{\operatorname{Re} }}_{b}}}}{{\left. {{{{\left( {\frac{{du}}{{dY}}} \right)}}^{{ - 1}}}} \right|}_{{Y = {{Y}_{f}}}}}.$$

It is well known and our preliminary calculations confirm that \(du{\text{/}}dY\) depends only slightly on Re. Thus, we can take

$$Q\frac{{u_{e}^{2}}}{{{{I}_{e}}}}\operatorname{Re} _{b}^{2} = Au(1 - u)\exp \left( { - {{{\left( {\frac{{u - {{u}_{f}}}}{\Delta }\frac{{{{T}_{f}}(\operatorname{Re} )}}{{{{T}_{f}}({{{\operatorname{Re} }}_{b}})}}\frac{{\operatorname{Re} }}{{{{{\operatorname{Re} }}_{b}}}}} \right)}}^{2}}} \right).$$
(1.3)

The parameters A, Δ, and uf were taken so that the temperature distribution corresponds to the temperature profile calculated in [17] for flame under the following conditions. Air flows past the flat porous plate and a mixture of nitrogen and hydrogen is injected through its pores, the mass concentration of hydrogen being equal to 0.4%. At the boundary layer edge the velocity is equal to 5 m/s, the maximum temperature is located at the height of 3.5 mm at the distance of 0.1 m from the leading plate edge. In [17] the calculations were carried out at Te = 293 K, Reb = 180, and the Mach number M \( \ll \) 1. The best correspondence between the temperature profiles obtained in [17] and in the present calculation was reached at A = 15.25, uf = 0.15, and \(\Delta = 0.158\) (Fig. 2).

Fig. 2.
figure 2

Comparison of the temperature distributions of the present calculations (1) with the calculated (2) and experimental (3) data [17].

Full size image

In Fig. 3 we have reproduced the velocity and temperature profiles (Figs. 3a and 3b, respectively) at the Reynolds number Re = 180 and various injection parameters j. As expected, in injection the inflection point appears in the velocity profile. With increase in j the distance of this point from the plate surface also increases. In this case, the temperature increases inside the boundary layer. Calculations show that at  j = 0.004 the Reynolds number increases from Re = 70 to Re = 180. This is equavalent to displacement downstream by approximately two times and it increases the maximum temperature inside the boundary layer approximately by 35%. This is in qualitative agreement with the data on diffuse flame in the boundary layer, for example, with the experiments [17] and the calculations [18].

Fig. 3.
figure 3

Distributions of the velocity (a), the temperature (b), and the product of density by vorticity (c) in the boundary layer at Re = 180 and various gas injection.

Full size image

The generalized inflection point and the presence of maximum or minimum in the product of density and vorticity \(K = \rho (du{\text{/}}dy) = {{\rho }^{2}}(du{\text{/}}dY)\), whose presence is the necessary condition of instability, play a particular role in the theory of “inviscid” instability. In Fig. 3c we have reproduced variation in K along the boundary layer. From this figure we can see that the location of maximum is displaced towards the outer boundary layer edge with increase in the injection intensity, whereas the location of minimum remains the same. The strong influence of injection on the location of the maximum, and the generalized inflection point can affect stability of boundary layer flow.

2 STABILITY OF THE BOUNDARY LAYER

In dimensionless representation the complete dynamic equations take the form:

$$\rho \frac{{d{\mathbf{v}}}}{{dt}} = - {\text{grad}}\Pi ,\quad \frac{{d\rho }}{{dt}} + \rho {\text{div}}({\mathbf{v}}) = 0,\quad \rho \frac{{dh.}}{{dt}} = \frac{{dp}}{{dt}} - {\text{div}}({\mathbf{q}}) + 2\mu {{\dot {S}}^{2}} + \rho Q,$$
(2.1)
$$\frac{d}{{dt}} = \frac{\partial }{{\partial t}} + u\frac{\partial }{{\partial x}} + {v}\frac{\partial }{{\partial y}}w\frac{\partial }{{\partial z}},\quad {{\dot {S}}_{j}} = \frac{1}{2}\left( {\frac{{\partial {{{v}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{v}}_{j}}}}{{\partial {{x}_{i}}}}} \right),\quad {{\dot {S}}^{2}} = \sum\limits_{i,j = 1}^3 {\dot {S}_{{ij}}^{2}} ,$$
$$\Pi = \left( {p + \frac{2}{3}\mu {\text{div}}{\mathbf{v}}} \right)E - 2\mu \dot {S},\quad p = \rho RT,\quad {\mathbf{q}} = - \frac{{{{c}_{p}}\mu }}{{\Pr }}{\text{grad}}T.$$

Here, the heat flux is divided by \({{\rho }_{e}}u_{e}^{3}\) and time by \({{{v}}_{e}}{\text{/}}u_{e}^{2}\). Normalization of other quantities is the same as that in (1.1). Any quantity \({{\Phi }_{j}}\) can be represented in form of the sum of the basic time-independent quantity and a time-dependent perturbation \({{\Phi }_{i}}(t,x,y,z) = {{\phi }_{i}}(x,y,z) + \varepsilon {{\phi }_{{1i}}}(t,x,y,z)\). Linearization of (2.1) with respect to perturbations \({{\phi }_{{1i}}} = \phi _{i}^{d}(y)\exp [i(ax + bz - Ft)\) leads to a linear system of differential equations [19, 20], which in the parallel flow approximation takes the form:

$$\frac{{d\phi _{1}^{d}}}{{dY}} = - {{i}_{c}}\phi _{2}^{d} + {{i}_{x}}\phi _{5}^{d} + {{i}_{z}}\phi _{6}^{d} - 2{{\mu }_{r}}\frac{{du_{w}^{d}}}{{dY}},\quad \frac{{d\phi _{2}^{d}}}{{dY}} = \rho \frac{{dT}}{{dY}}\phi _{2}^{d} - u_{w}^{d} - {{i}_{c}}T{{r}^{d}},$$
$$\frac{{d\phi _{3}^{d}}}{{dY}} = - {{i}_{x}}\phi _{2}^{d} - \frac{{du}}{{dY}}{{\mu }_{t}}{{T}^{d}} + \frac{{\phi _{5}^{d}}}{{{{\mu }_{r}}}},\quad {\text{ }}\frac{{d\phi _{4}^{d}}}{{dY}} = - {{i}_{z}}\phi _{2}^{d} + \frac{{\phi _{6}^{d}}}{{{{\mu }_{r}}}},$$
$$\frac{{d\phi _{5}^{d}}}{{dY}} = {{i}_{x}}\phi _{1}^{d} + {{i}_{c}}\phi _{3}^{d} - i_{T}^{d} + \rho \frac{{du}}{{dY}}\phi _{2}^{d},\quad \frac{{d\phi _{6}^{d}}}{{dY}} = {{i}_{z}}\phi _{1}^{d} + \left( {{{i}_{c}} - {{\mu }_{a}}} \right)\phi _{4}^{d} - {{i}_{z}}{{\mu }_{r}}u_{w}^{d},$$
(2.2)
$$\frac{{d\phi _{7}^{d}}}{{dY}} = i\omega RT\phi _{1}^{d} + \rho \frac{{dI}}{{dY}}\phi _{2}^{d} - ui_{t}^{d} + {{i}_{c}}u\phi _{3}^{d} + \left( {{{i}_{c}} - \frac{{{{\mu }_{a}}}}{{\Pr }}} \right)\phi _{8}^{d},$$
$$\frac{{d\phi _{8}^{d}}}{{dY}} = - \Pr \frac{{du}}{{dY}}\phi _{3}^{d} - \frac{{dh}}{{dY}}{{\mu }_{t}}{{T}^{d}} + \frac{{\Pr \left( {\phi _{7}^{d} - u\phi _{5}^{d}} \right)}}{{{{\mu }_{R}}}}.$$

Here, \(\phi _{1}^{d}\), \(\phi _{2}^{d}\), \(\phi _{3}^{d}\), \(\phi _{4}^{d}\), \(\phi _{5}^{d}\), \(\phi _{6}^{d}\), \(\phi _{7}^{d}\), and \(\phi _{8}^{d}\) are the amplitudes of perturbations of the pressure, the normal, streamwise, and lateral velocities, the shear stresses τ12 and τ23, the heat flux, and the enthalpy. The additional terms of the system are as follows:

$$u_{w}^{d} = {{i}_{x}}\phi _{3}^{d} + {{i}_{z}}\phi _{5}^{d},\quad i_{t}^{d} = {{i}_{x}}{{\mu }_{r}}u_{w}^{d} + {{\mu }_{a}}\phi _{3}^{d},$$
$${{\mu }_{a}} = (i_{x}^{2} + i_{z}^{2}){{\mu }_{r}},\quad \tilde {r} = {{\rho }^{d}}{\text{/}}\rho = {{g}_{m}}\phi _{1}^{d} - \rho {{T}^{d}},$$
$${{T}^{d}} = {{g}_{{m1}}}\phi _{8}^{d},\quad {{i}_{x}} = ia\operatorname{Re} T,\quad {{i}_{z}} = ib\operatorname{Re} T,$$
$${{i}_{c}} = \operatorname{Re} {{u}_{c}} = i\operatorname{Re} (ua - F),\quad {{\mu }_{r}} = \frac{{\mu \rho }}{{\operatorname{Re} }},\quad {{\mu }_{T}} = \frac{1}{\mu }\frac{{d\mu }}{{dT}},$$
$${{g}_{m}} = \gamma {{M}^{2}},\quad {\text{ }}{{g}_{{m1}}} = (\gamma - 1){{M}^{2}},\quad \gamma = {{c}_{p}}{\text{/}}{{c}_{{v}}},$$

where γ is the specific heat ratio.

The system (2.2) is solved with the boundary conditions

$$\phi _{3}^{d},\phi _{2}^{d},\phi _{4}^{d},\phi _{8}^{d} = 0\quad (Y = 0\;\,{\text{and}}\,Y = \infty ).$$
(2.3)

For given values of M, Re, F, and the main flow parameters the solution of system (2.2) with conditions (2.3) exist for the eigenvalue a = ar + iai. Flow is unstable for negative ai.

In Fig. 4 we have reproduced the degrees of spatial amplification of perturbations as functions of the frequency parameter at Re = 180,  j = 0.004, and various angles of wave slip χ = arctan(b/ar).

Fig. 4.
figure 4

Degree of spatial amplification as a function of the frequency parameter for various slip angles: Re = 180 and j = 0.004.

Full size image

From these data we can see that the two-dimensional waves, χ = 0, grow most intensively almost over the entire increasing perturbation frequency range. Therefore, in what follows we will give the results of stability only with respect to two-dimensional perturbations.

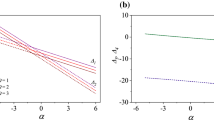
In Fig. 5 we have reproduced the degrees of amplification as functions of the frequency for a series of the Reynolds numbers. From these data we can see that the maximum degree of amplification increases with the Reynolds number at Re < 150, its further increase leads to a decrease in the perturbation growth rate. The frequency of most growing waves decreases with increase in the Reynolds number, obviously, due to the growth in the boundary layer thickness with increase in Re = x1/2.

Fig. 5.
figure 5

Degree of spatial amplification as a function of the frequency parameter for various Reynolds numbers: j = 0.004 and χ = 0.

Full size image

In Fig. 6 we have reproduced the degree of spatial amplification as a function of the frequency parameter for various gas injection through the porous wall at Re = 180. As in the absence of heating [21], in the presence of heat supply an increase in the mass flow rate through the wall leads to destabilization of flow. In calculations it was established that at j = 0.004 the critical Reynolds number decreases by almost 70% as compared with the case j = 0.

Fig. 6.
figure 6

Degree of spatial amplification as a function of the frequency parameter for various gas injection through the porous wall: Re = 180 and χ = 0.

Full size image

The calculations of the phase and group velocities as functions of the frequency parameter in the unstable domain at Re = 180 and  j = 0.004 showed that, primarily, the group velocity is significantly higher than the phase velocity. As the frequency increases, the phase velocity tends to the main flow velocity in the position of maximum of the function K. It is located in the velocity interval at the position of the minimum and maximum K (Fig. 3c, Re = 180 and j = 0.004), where the second necessary condition of “inviscid” instability [15], \((u - Us)(dK{\text{/}}dY) < 0\), is fulfilled; this condition is a generalization of the Fjortoft criterion [22]. Here, Us is the velocity corresponding to the maximum of K.

It is known [23] that for weak amplification of perturbations their spatial and time degrees of amplification are connected by the relation ai ≈ –Fi/Cgr, in which the time degree of amplification Fi is the imaginary part of the eigenvalue F of the problem (2.2), (2.3) for a fixed real a. Special calculations showed that the exact value of the degree of spatial amplification almost coincides with its approximate value even for fairly intensive growth in the perturbtion amplitude.

In [13, 24], in investigating the influence of heat supply in the absence of gas injection through the plate surface, it was established the stabilizing role of heating the narrow band of the boundary layer. Therefore, in the present studies we have also paid attention to the effect of heating on stability of the boundary layer under the conditions of gas injection through the porous plate. In Fig. 7 we have reproduced the degrees of amplification as functions of the frequency for various ratios of amounts of the injected gas ( j = 0, 0.001, and 0.004), both in the absence of heat supply (Q = 0) and in the presence of heat supply in accordance with relation (1.3). In this case all the dependences were obtained at the same wall temperature Tw = 2.16 (640 K) and the Reynolds number Re = 180. Comparison of the maxima of these dependences shows the following. In the absence of heat supply (curves 1 ( j = 0.004), 2 ( j = 0.0), and 5 ( j = 0)) gas injection destabilizes flow. On the contrary, heat supply stabilizes flow in the case of heated plate (Tw = 2.16). A comparison of curves 1 and 4 shows that in the case of large amount of injected gas ( j = 0.004) heat supply decreases the maximum degree of amplification by a factor of more than two. However, the degree of amplification is still higher than in the case without heating and gas injection (curve 2). For the smaller amounts of injected gas ( j = 0.001), as a result of heat supply (curve 6), stability of the boundary layer increases not only in the case without heat supply (curve 5), but the boundary layer becomes more stable as compared with the case without injection and heat supply (curve 2).

Fig. 7.
figure 7

Degree of spatial amplification as a function of the frequency parameter for various ratios of gas injection through the wall and heat supply (Re = 180, Tw = 2.16, and χ = 0): curve 1 corresponds to j = 0.004 and Q = 0; curve 2 to j= 0 and Q = 0; curve 3 to j = 0 and Q ≠ 0; curve 4 to j = 0.004 and Q ≠ 0; curve 5 to j = 0.001 and Q = 0; and curve 6 to j = 0.001 and Q ≠ 0.

Full size image

SUMMARY

The temperature profile of the diffuse flame [17] is simulated for the mass gas injection through the porous plate j = (ρ\({v}\))w/(ρu)∞ = 0.004, the Reynolds number Re = 180, and the Mach number M \( \ll \) 1 within the framework of the local self-similar approximation. In this case heat supply is required in accordance with (1.3). Using (1.3), the time-independent parameters of the boundary layer were calculated and its stability was considered at various Reynolds numbers and flow rate of the gas injected through the porous wall. It is found that increase in the injected gas mass leads to formation of inflection velocity profiles. At a fixed injection rate an increase in the Reynolds number increases the maximum temperature inside the layer. From this fact there follows the growth in the maximum temperature downstream since \({\text{Re}} = {{x}^{{1/2}}}\). This is observed in diffuse combustion, for example, in experiments [17] and calculations [18]. An important function in the “inviscid” instability theory, namely, the product of density and vorticity K, has two generalized inflection points. One of them corresponds to the minimum and the second point to the maximum of K(Y). The minimum of K is located at the smaller distance from the wall as compared with the location of the maximum of K. As the injection increases, the maximum is displaced towards to outer boundary layer edge, whereas the minimum continues to remain at Y ≈ 1.

Stability of the boundary layer with heat supply and gas injection is first investigated for subsonic flow past the plate. As a result of investigations, it was found that under the conditions of gas injection and internal heat supply the most dangerous (growing) perturbations are two-dimensional, the same is valid in the absence of heating. There exists a Reynolds number at which the degree of amplification is maximum. With increase in the Reynolds number the frequency of the most growing waves decreases due to increase in the boundary layer thickness. Gas injection destabilizes the boundary layer. For the injection parameter j = 0.004 the critical Reynolds number decreases by approximately 40% as compared with the case j = 0.

The critical layer, in which the boundary layer velocity is equal to the phase velocity of wave (u = C), is located in the region that corresponds to the second necessary condition of “inviscid” instability, \((u - Us)(dK{\text{/}}dY) < 0\). With increase in the frequency of growing waves, the phase velocity tends to the flow velocity at the maximum of the product of density and vorticity that corresponds to the generalized inflection point. Regardless the fairly high degrees of spatial growth, their approximate values, determined as the ratio of the degree of time amplification to the group velocity, almost coincide with the exact quantities.

In the case of the heated plate, heat supply inside the boundary layer reduces the maximum perturbation growth rate in the boundary layer with gas injection, as well as in the case of its absence.