Instabilities, Bifurcations, and Nonlinear Dynamics in Two-Dimensional Generalizations of Kolmogorov Flow

Abstract

A family of two-dimensional flows of viscous incompressible fluid in a plane rectangular region with periodic boundary conditions (two-dimensional torus) is considered. The flows are induced by a force, periodic in the two spatial variables and independent of time. In the particular case of the harmonic dependence of the force on one coordinate and in the absence of average flow the well-known Kolmogorov flow is realized. In the general two-dimensional case restructurings of the stationary solutions of the Navier–Stokes equations are investigated numerically and the stability domains are determined in the space of governing physical and geometric parameters, namely, Reynolds numbers, force amplitudes, and spatial dimensions of periodicity cells. It is found that in a square region, whose side is equal to the spatial period of the external force, the main stationary flow preserves its stability against variation in the force amplitude and the Reynolds number. Contrariwise, in the cells, whose sides include several force periods, the variation in the parameters destabilizes the stationary flow. Stationary and self-oscillatory nonlinear secondary flows are considered. The effect of nonstationarity on the Lagrangian dynamics is discussed: the mechanisms of transition to the chaotic advection of passive particles depend on the commensurability of the Reynolds numbers characterizing the average flow in mutually perpendicular directions.

Two-dimensional flows of viscous incompressible fluid induced by a time-independent, spatially-periodic force in the presence of constant pumping along mutually perpendicular directions are two-dimensional generalizations of the well-known spatially-periodic Kolmogorov flow [1] proposed as a model of the cascade energy transfer in turbulent flows. In [2—4] the boundaries of the monotonic stability of the Kolmogorov flow were determined, its longwave nature was established, and secondary spatially-periodic near-threshold flows were studied. In the further theoretical and numerical studies it was shown that the introduction of lateral boundaries reduces considerably the wave length of dangerous perturbations [5] and at high Reynolds numbers leads to the generation of a coherent large-scale vortex [6]. Various unsteady flows were also found, including quasiperiodic and intermittent states [7].

Similar structures were also realized in experiments [8–11] with magnetohydrodynamic flows in thin layers of a weakly conducting fluid, where the main flow instability and the transition to secondary flows with periodicity in two coordinates were confirmed.

For certain force configurations there are known steady solutions of the Navier–Stokes equations, in which the velocity field is doubly periodic and the periods in each coordinate are multiple to the spatial force period, in particular, the two-vortex flow with pumping in two directions [12] and the single-vortex flow of the “cat’s eye” type [13]. The Lagrangian dynamics of passive admixture particles is unusual in a certain parameter domain, its properties being intermediate between laminar and turbulent flows, such as the fractal spectrum of the transported particle velocities, anomalous characteristics of the transport, etc. The known particular cases of these flows are the Kolmogorov flow (in what follows, K59) [1] and the flow with two-component doubly periodic imposed force (in what follows, ZPK96) [12]. In both cases, the basic solution with the stream function periodic in one or two coordinates is stable against the perturbations, whose wavelength is not greater than the imposed force period, and exhibits longwave instability, which is monotonic for K59 [2], and, depending on the pumping parameters, either monotonic or oscillatory for its two-dimensional generalizations [14].

The studies described above showed the necessity of a more profound investigation of the stability of the known stationary flows and the development of secondary flow patterns and the corresponding Lagrangian dynamics. Below, for the ZPK96 flow, with account for nonzero fluid flow rate in the x and y directions parametrized in terms of the Reynolds numbers Re_x and Re_y, the stability of the basic and secondary flow families is investigated, the nonlinear development of the secondary states after the loss of stability is considered, and an analysis of qualitative variations in the Lagrangian dynamics of transported particles is carried out.

1 FORMULATION OF THE PROBLEM

We consider a two-dimensional flow of a viscous incompressible fluid in a rectangular cell of an infinite layer with periodicity conditions in the х and у coordinates (two-dimensional torus). The flow is induced by a time-independent and spatially doubly periodic force ${\mathbf{F}}(x,y)\, = \,({{f}_{1}}\sin {\kern 1pt} ({y \mathord{\left/ {\vphantom {y {L)}}} \right. \kern-0em} {L)}},{{f}_{2}}\sin ({x \mathord{\left/ {\vphantom {x {L)}}} \right. \kern-0em} {L)}})$. In the dimensional variables the Navier—Stokes equations for the velocity ${\mathbf{v}} = \left\{ {{{{v}}_{x}},{{{v}}_{y}}} \right\}$ take the form:

$$\begin{gathered} \frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}}\nabla ){\mathbf{v}} = - \frac{{\nabla p}}{{{{\rho }_{f}}}} + \nu \Delta {\mathbf{v}} + {\mathbf{F}}, \\ \operatorname{div} {\mathbf{v}} = 0, \\ \end{gathered} $$

(1.1)

while the periodicity conditions and the imposed fluid flow rates in perpendicular directions read as follows:

$$\begin{gathered} {\mathbf{v}}(x + {{L}_{x}},y) = {\mathbf{v}}(x,y + {{L}_{y}}) = {\mathbf{v}}(x,y)\quad \forall x,y; \\ \frac{1}{{{{L}_{x}}}}\int\limits_0^{{{L}_{x}}} {dx} \int\limits_0^{{{L}_{y}}} {{{{v}}_{x}}dy} = \alpha ,\quad \frac{1}{{{{L}_{y}}}}\int\limits_0^{{{L}_{y}}} {dy} \int\limits_0^{{{L}_{x}}} {{{{v}}_{y}}dx} = \beta . \\ \end{gathered} $$

Here, ν is kinematic viscosity, ρ_f is the fluid density, L_x and L_y are the dimensional length and width of a periodicity cell; L/(2π),  f₁, and  f₂ are the dimensional spatial period and amplitudes of the external force, and α and β are the dimensional flow rates in the x and y directions, respectively.

In the dimensionless form Eqs. (1.1) written in terms of the stream function $\Psi (x,y)$, for which ${{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial y = }}} \right. \kern-0em} {\partial y = }}{{{v}}_{x}},$ and ${{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial x = }}} \right. \kern-0em} {\partial x = }} - {{{v}}_{y}},$ are as follows:

$$ - \frac{{\partial \Delta \Psi }}{{\partial t}} - \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \Delta \Psi }}{{\partial x}} + \frac{{\partial \Psi }}{{\partial x}}\frac{{\partial \Delta \Psi }}{{\partial y}} + \Delta \Delta \Psi = - {{\lambda }_{1}}\cos y + {{\lambda }_{2}}\cos x,$$

(1.2)

while the fluid flow rates in the perpendicular directions are, respectively, as follows:

$$\frac{1}{{{{l}_{x}}}}\int\limits_0^{{{l}_{x}}} {dx} \left( {\Psi (x,{{l}_{y}}) - \Psi (x,0)} \right) = {{\operatorname{Re} }_{x}};\quad - \frac{1}{{{{l}_{y}}}}\int\limits_0^{{{l}_{y}}} {dy} \left( {\Psi ({{l}_{x}},y) - \Psi (0,y)} \right) = {{\operatorname{Re} }_{y}}.$$

(1.3)

Problem (1.2), (1.3) is characterized by the following dimensionless parameters:

the Reynolds numbers Re_x = α/ν and Re_y = β/ν;

the external force with the components λ₁ = f₁L³/ν² and λ₂ = f₂L³/ν²; and

the cell dimensions l_x = L_x/L and l_y = L_y/L.

It is convenient to decompose the stream function into the terms linear in х and у, which ensure the pumping, and a part periodic with respect to the both coordinates: $\Psi (x,y) = {{\operatorname{Re} }_{x}}y - {{\operatorname{Re} }_{y}}x + \Psi {\kern 1pt} '(x,y)$. Then the conditions of the velocity field periodicity can be written in the form: Ψ'(x + l_x, y) = $\Psi {\kern 1pt} '(x,y + {{l}_{y}})$ = Ψ'(x, y).

2 THE KNOWN STATIONARY SOLUTIONS AND THEIR STABILITY

The particular solutions of problem (1.2) are the Kolmogorov flow K59 [1] (λ₂ = Re_x = Re_y = 0) and the ZPK96 flow in a square region with periodic boundary conditions, which is equivalent to a flow over the two-dimensional torus surface [12] (λ₁ = λ₂ = λ). In both cases, stationary solutions of problem (1.2) are known. In the former case, this is ${{\Psi }_{0}}(x,y)\, = \,\lambda {{{\kern 1pt} }_{1}}\cos (y)$, which, as shown in [2–4], is stable at l_x < 2π. The longwave instability (l_x → ∞) was obtained at ${{\lambda }_{{{\text{1cr}}}}} = \sqrt 2$; for the cells of finite length l_x > 2π the oscillatory instability was found in [15] and for a more general case, at nonzero flow rate Re_x in [14]. The stationary ZPK96 solution [12] at l_x = l_y = 2π takes the form:

$$\begin{gathered} {{\Psi }_{0}}(x,y) = {{\operatorname{Re} }_{x}}y - {{\operatorname{Re} }_{y}}x + \lambda \frac{{\sin (x + {{\phi }_{x}})}}{{\sqrt {\operatorname{Re} _{x}^{2}\; + 1} }} - \lambda \frac{{\sin (y + {{\phi }_{y}})}}{{\sqrt {\operatorname{Re} _{y}^{2}\; + 1} }}, \\ {{\phi }_{x}} = {\text{arctan}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{x}}}}} \right);\quad {{\phi }_{y}} = {\text{arctan}}\left( {\frac{1}{{{{{\operatorname{Re} }}_{y}}}}} \right). \\ \end{gathered} $$

(2.1)

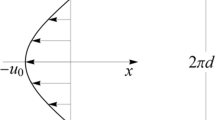
In the absence of an external force (λ = 0) the trivial flow on the two-dimensional torus is realized; it is characterized by the rotation number ρ = Re_x/Re_y, rectilinear streamlines, and uniform velocity. The flow is “global”: a fluid particle, set initially at any point in the region, is carried around the torus again and again and, in the case of irrational rotation number, passes arbitrarily close to any given point. As shown in [12], with increase in the force amplitude λ the streamlines become curved and at λ = λ_cr = $\sqrt {\operatorname{Re} _{x}^{2}\,\operatorname{Re} _{y}^{2} + \max (\operatorname{Re} _{x}^{2},\operatorname{Re} _{y}^{2})}$ the topological restructuring takes place: the cusp points appear on two streamlines. Each of them is the flow stagnation point, where both velocity components vanish simultaneously. With further increase in λ the degenerate stagnation points break down into saddle and elliptic stagnation points with the formation of a “local” flow structure on the torus surface, apart from the “global” structure. This local structure is formed by two vortices filled with closed streamlines around the elliptic points. The vortices separated from the global flow component by the separatrices of the saddle points are small immediately after their birth but they enlarge with increase in λ occupying gradually an increasingly greater portion of the periodicity cell area. At λ > λ_cr and irrational rotation numbers the global flow component supports nontrivial Lagrangian dynamics: since every streamline in the global component passes again and again arbitrarily close to the fixed saddle point, in the trajectory of the particle transported along this line the epochs of relatively rapid drift alternate with decelerations, down to almost complete stopping. This leads to an attenuation of temporal correlations and causes an anomalous transport of tracer particles in the subdiffusion regime. We note that the restructuring of the flow topology at λ = λ_cr, is not a bifurcation, despite the profound variations introduced by it into the dynamics: the new solutions do not branch off, whereas the stability of the existing solution does not change.

We performed a numerical investigation of problem (1.2). The stationary solutions of the system (apart from solution (2.1)) were determined using the multidimensional Newton method applied to the system of algebraic equations of the discrete counterpart of (2.1) [16].

We expand the spatially periodic part of the stream function $\Psi {\kern 1pt} '(x,y)$ in the Fourier series

$$\Psi {\kern 1pt} '(x,y,t) = \sum\limits_{m = - M}^M {\sum\limits_{n = - N}^N {{{\psi }_{{m,n}}}(t){{e}^{{\frac{{imx}}{{l_{x}^{'}}} + \frac{{iny}}{{l_{y}^{'}}}}}}} } ;\quad l_{x}^{'} = \frac{{{{l}_{x}}}}{{2\pi }};\quad l_{y}^{'} = \frac{{{{l}_{y}}}}{{2\pi }}.$$

(2.2)

Substituting Eq. (2.2) into Eq. (1.2) and applying the standard procedure of multiplying by a complex exponential to the system of equations thus obtained, followed by integration over the torus surface we obtain (2M + 1) × (2N + 1) – 1 ordinary differential equations governing the temporal evolution of the coefficients of the Fourier series

$$\begin{gathered} \left( {\frac{{{{m}^{2}}}}{{l_{x}^{{'2}}}} + \frac{{{{n}^{2}}}}{{l_{y}^{{'2}}}}} \right)\left( {\frac{d}{{dt}} + \frac{{{{m}^{2}}}}{{l_{x}^{{'2}}}} + \frac{{{{n}^{2}}}}{{l_{y}^{{'2}}}} + \frac{{im}}{{l_{x}^{'}}}{{{\operatorname{Re} }}_{x}} + \frac{{in}}{{l_{y}^{'}}}{{{\operatorname{Re} }}_{y}}} \right){{\psi }_{{m,n}}} \\ \, - \sum\limits_{{{m}_{1}} = \max \left( { - M,m - M} \right)}^{\min \left( {M,m + M} \right)} {\sum\limits_{{{n}_{1}} = \max \left( { - N,n - N} \right)}^{\min \left( {N,n + N} \right)} {\frac{{{{n}_{1}}m - {{m}_{1}}n}}{{l_{x}^{'}l_{y}^{'}}}\left( {\frac{{{{{\left( {m - {{m}_{1}}} \right)}}^{2}}}}{{l_{x}^{{'2}}}} + \frac{{{{{\left( {n - {{n}_{1}}} \right)}}^{2}}}}{{l_{y}^{{'2}}}}} \right){{\psi }_{{{{m}_{1}},{{n}_{1}}}}}{{\psi }_{{m - {{m}_{1}},n - {{n}_{1}}}}}} } + {{F}_{{m,n}}} = 0. \\ \end{gathered} $$

(2.3)

Here, ${{F}_{{m,n}}}$ = 0 for all m and n, apart from ${{F}_{{l_{x}^{'},0}}} = {{F}_{{ - l_{x}^{'},0}}} = - \frac{{{{\lambda }_{2}}}}{2}$ and ${{F}_{{0,l_{y}^{'}}}} = {{F}_{{0, - l_{y}^{'}}}} = \frac{{{{\lambda }_{1}}}}{2}$. The primed indices are integer-valued by virtue of the choice of the periodicity cell sides (length l_x  and width l_y) and determine how many force periods (2π) they contain.

The criterion for the mode numbers M and N in the expansion of Ψ′ in the Fourier series is the accuracy of determining the critical force amplitude values corresponding to different kinds of destabilization of flow (2.1). At M = N = 5 eight decimal points are correctly determined in the critical value of λ, while the use of numbers M and N greater than 15 displaces the threshold values by a value comparable with the round-off error. To produce a “margin of safety” for accurately determining unsteady solutions we used in our calculations the values M = N = 20.

The linearization of Eq. (2.3) near the stationary solution (2.1) characterizes the stability within the framework of the Navier–Stokes equations. We determined the stability domains in the space of the parameters Re_x, Re_y, and λ. In particular, a somewhat unexpected fact was established in the calculations: in a square cell with the side lengths equal to the imposed force period (${{l}_{x}} = {{l}_{y}} = 2\pi$) the stationary solution (2.1) is stable even at fairly large values of the force amplitude 0 ≤ λ ≤ 100 and in a wide flow rate range –10 ≤ (Re_x, Re_y) ≤ 10. An increase in the cavity dimensions up to several periods of the imposed force opens possibilities for longwave perturbations; the calculations showed that, in particular, in rectangular periodicity cells (${{l}_{x}} = 2\pi m,$ ${{l}_{y}} = 2\pi n;$ $\max (m,n) > 1;$ $m,n \in \mathbb{N}$) the destabilization of flow (2.1) is possible and the secondary solutions can be both stationary and self-oscillatory in nature, depending on the problem parameters (Fig. 1).

Fig. 1.

Instability thresholds of the K59 and ZPK96 flows as functions of the periodicity cell length l_x (a); pattern of the basic flow ZPK96 (b) and its critical perturbations at l_x/2π = 2 (c) and l_x/2π = 3 (d) for l_y = 2π.

With variation in the periodicity cell length l_x from 2π to l_x → ∞ at a fixed width l_y = 2π the instability threshold decreases monotonically from ${{\lambda }_{{{\text{inst}}}}}\, \to \;\infty$ for the square cell to the value ${{\lambda }_{{{\text{inst}}}}} = \sqrt 2$ corresponding to the threshold of the Kolmogorov flow K59.

In Fig. 2 the dependences of the critical force amplitude value λ and the neutral perturbation frequency ω on the pumping parameters Re_x and Re_y are illustrated for the cell with l_x = 4π and l_y = 2π. For the sake of comparison, in the same figure the values of  λ_cr corresponding to the generation of stationary vortices in the flow structure (2.1) are presented.

Fig. 2.

Neutral curves in the (Re_x, λ), (Re_y, λ), and (Re_x, Re_y) planes (the upper row, from left to right) and dependence of the critical perturbation frequency on Re_x and Re_y. The dotted curves correspond to λ_cr.

It can be seen that both oscillatory and monotonic instabilities of solution (2.1) are possible with the instability thresholds λ₀ and λ_m, respectively. Different ordering of these threshold values is possible both between each other and with the value λ_cr, at which localized stationary vortices are formed in the flow structure (2.1) against the background of the global component. The results of the linear analysis allow us to conclude that the instability of this flow for the geometry considered (l_x = 4π and l_y = 2π) is mainly determined by the parameter of the pumping along the х axis Re_x; an increase in Re_y leads to considerable flow stabilization. In the absence of the pumping it is the monotonic instability that is always realized; with increase in Re_x the oscillatory instability modes appear. Below we consider different versions of instability development and study the corresponding types of secondary nonlinear flow patterns on the basis of a numerical analysis of the complete nonlinear equations (2.3). In the calculations we used the multidimensional Newton method [14, 16] for determining stationary solutions and eigenvalues λ and the Runge–Kutta–Fehlberg method with an adaptive time step for numerically integrating Eq. (2.3) in the case of unsteady (in particular, oscillatory) solutions in combination with the method of continuation (tracking) along parameters and identification of bifurcations via the spectrum of Jacobian eigenvalues.

3 BIFURCATIONS AND SECONDARY FLOWS

To illustrate the restructuring of flow patterns we choose a cell with the aspect ratio 2 : 1, so that two periods of the stationary external force are contained in its length (along the x coordinate) and one force period is contained in its width (coordinate y). The stationary flow (2.1) is symmetric with respect to a doubled cell with periodic boundary conditions in x: it is invariant with respect to the displacement by half cell length. Accordingly, Eqs. (2.3) written in terms of the Fourier coefficients ${{\psi }_{{m,n}}}$ are invariant with respect to the sign reversal of all coefficients with odd values m, while the spontaneous violation of this symmetry in the case of monotonic perturbation increase leads to the pitchfork bifurcation of the equilibrium state.

Figure 3 presents the map of the main flow types for such a cell at a fixed pumping intensity along the coordinate y: Re_y = 1. The stability domain of solution (2.1) is highlighted by the grey background.

Fig. 3.

Map of states in the plane of the flow parameters (Re_x, λ) in the periodicity cell with l_x = 4π and l_y = 2π at the fixed mean flow rate Re_y = 1. The stationary flow (2.1) is stable in the domain with the gray background. The bifurcation curves correspond to the following situations: B_1,2 are the pitchfork bifurcations of stationary flows, AH_1,2 relates to the onset of self-oscillations (Andronov–Hopf bifurcation), and SN_1,2,3 are the saddle-node bifurcations of the finite-amplitude birth of stationary flows. The black circles BT_1,2 are the points of Bogdanov–Takens bifurcations. The dashed line (a) corresponds to the λ_cr value, at which a vortex pair is formed in flow (2.1). Panel (a) represents the general view in the logarithmic coordinates, panel (b) is the region around point BT₁, and panel (c) is the region near the cusp point formed by lines SN₁ and SN₂.

As shown in the left (a) and central (b) panels of the figure, at small Re_x the instability of flow (2.1) is monotonic and is accompanied by pitchfork bifurcations B₁ and B₂ generating symmetric pairs of stationary flows (the elements of a pair turn into one another under translation by 2π along the x axis). The bifurcation B₁ is supercritical and the bifurcation B₂ is subcritical, so that the branches of the stationary solutions born from (2.1) on line B₁ terminate on B₂. At Re_x = 0.1233 the B₁ and B₂ lines coalesce and above this Re_x value the pitchfork bifurcations of flow (2.1) do not occur. But somewhat earlier, at Re_x = 0.1189 an another determining event takes place on the line B₁: at point BT₁ two eigenvalues of the linearized problem simultaneously vanish. As a result of this phenomenon of codimension 2, known as the Bogdanov–Takens bifurcation [17], the bifurcation scenario changes: at higher Re_x values the instability of flow (2.1) is oscillatory, so that on line AH₁ the Andronov–Hopf bifurcation generates a stable limiting cycle from the equilibrium corresponding to flow (2.1) and the flow structure oscillates periodically.

Due to the above-mentioned symmetry of flow (2.1), the Bogdanov–Takens bifurcation at point BT₁ is non-generic [17]. Since the primary solution does not vanish on B₁ but only loses stability, as can be seem in the middle panel in Fig. 3b, the line AH₁ proceeding to the right from point BT₁ is continued into the range of smaller Re_x values: this is line AH₂, on which the Andronov–Hopf bifurcation occurs with secondary stationary flows having branched from (2.1) on B₁ line.

Apart from the bifurcations having a direct effect on the main flow (2.1), at small Re_x values there occurs also the finite-amplitude birth/vanishing of secondary stationary flows. It occurs as a result of saddle-node bifurcations on SN₁ and SN₂ lines. The SN₁ and SN₂ lines terminate at the cusp point at Re_x = 0.1133; in the wedge formed by these lines multistability takes place: coexistence of several stable stationary flows at fixed parameter values. As can be seen in the right panel of Fig. 3c, the AH₂ line of the Andronov–Hopf bifurcation also enters this wedge from the right. This line terminates on SN₂ at point BT₂ of the other Bogdanov–Takens bifurcation occurring with secondary stationary flows. Thus, both end points on line AH₂ in the parameter plane are the Bogdanov–Takens points. Since the secondary stationary flows do not possess the symmetry against the spatial displacement, the bifurcation BT₂ (as distinct from BT₁) is general in nature.

The upward motion along the SN₁ line leads to a variation in the nature of the saddle-node bifurcation occurring on it: in the phase space it becomes global from local (coalescence of two equilibria) and involves a homoclinic trajectory toward the saddle-node point. The breakdown of this trajectory, which is frequently called the SNIC bifurcation in the literature (Saddle-Node on Invariant Circle), generates a stable periodic motion, whose period increases without bound, as the bifurcation value of the parameter is approached. At Re_x = 0 (the absence of a mean flow rate along the x axis) the main flow possesses one more symmetry, namely, the invariance with respect to the mirror reflection relative to the line parallel to the y axis. This symmetry is also inherited by the secondary stationary flows occurring upon saddle-node bifurcations. For this reason, the monotonic instability of these flows leads to a new pitchfork bifurcation and the generation of pairs of mirror-symmetric tertiary stationary flows. At arbitrarily small, nonzero values of the pumping along the x axis the symmetry is absent and the pitchfork bifurcation is broken up being replaced by one more saddle-node bifurcation (line SN₃ in Fig. 3). In Fig. 3a we also present the line, on which the change of the topological structure of the main flow (2.1) described above takes place: the birth of stagnation points and stationary vortices. It can be seen that at sufficiently large Re_x values the oscillatory instability of the main stationary flow can precede this restructuring.

In Fig. 4 we present several typical bifurcation diagrams corresponding to the motion along the vertical lines in Fig. 3: an increase in the force amplitude λ at a fixed value of the parameter Re_x. The quantity $\delta = {{v}_{y}}\left( {0,0} \right) - {{v}_{{y0}}}\left( {0,0} \right)$ is used as the quantitative flow characteristic (here and below, the subscript 0 indicates the characteristics of the main flow (2.1.)). For stationary flows δ corresponds to the deviation of the y-component of the flow velocity from the value corresponding to the basic stationary flow (2.1); an oscillatory flow is characterized by maximum (δ_max) and minimum (δ_min) values of this deviation during the period, as well as the period value T. Moreover, in constructing the phase trajectories the Eulerian variables $\left( {\Delta {{v}_{x}},\Delta {{v}_{y}},\Delta {{\Psi }_{c}}} \right)$ are used, where

$$\begin{gathered} \Delta {{v}_{x}} = {{v}_{x}}\left( {0,0} \right) - {{v}_{{x0}}}\left( {0,0} \right),\quad \Delta {{v}_{y}} = \delta , \\ \Delta {{\psi }_{c}} = \left( {\psi \left( {\frac{{{{L}_{x}}}}{2},\frac{{{{L}_{y}}}}{2}} \right) - \psi \left( {0,0} \right)} \right) - \left( {{{\psi }_{0}}\left( {\frac{{{{L}_{x}}}}{2},\frac{{{{L}_{y}}}}{2}} \right) - {{\psi }_{0}}\left( {0,0} \right)} \right). \\ \end{gathered} $$

Fig. 4.

Bifurcation diagrams δ(λ) of the flow in the periodicity cell with l_x = 4π and l_y = 2π at the fixed mean flow rate Re_y = 1 and the characteristic values of the mean flow rate Re_x. Solid, dotted, and dashed curves relate to stable stationary, unstable stationary, and stable self-oscillatory flows, respectively. Bifurcations B_1,2,3 are the pitchfork bifurcations of stationary flows, SN_1,2,3 are the saddle-node bifurcations of the finite-amplitude birth of stationary flows, and AH_1,2 are the Andronov–Hopf bifurcations (the onset of self-oscillations). (a), Re_x = 0; (b), Re_x = 0.01; (c, d), Re_x = 0.115; (e), Re_x = 0.125; (f), ${\text{R}}{{{\text{e}}}_{x}}\; = ~(\sqrt 5 \; - 1){\kern 1pt} /{\kern 1pt} 2$. Panels (g, h, and i) present the dependence of the oscillation period on the force amplitude λ (Re_x = 0.115 (g, h) and 0.125 (i).

In the same figure the corresponding dependences T(λ) are presented in the case of oscillatory solutions. The solid and dotted curves characterize stable and unstable stationary flows, respectively, and the dashed curves correspond to stable self-oscillatory states. The pitchfork bifurcations are marked by the symbols B₁ and B₂ on the bifurcation diagrams in Fig. 4, while the Andronov–Hopf bifurcations are marked by the symbols AH₁ and AH₂. The bifurcations of the both types can be either supercritical (B₁) or subcritical (B₂, AH₁, and AH₂). The saddle-node bifurcations are marked by the symbols SN₁, SN₂, …; they also include the above-mentioned SNIC bifurcation, when a saddle-node appears on an invariant cycle (Figs. 4c and 4d at λ ≈ 6.3 and Fig. 4g at λ ≈ 11).

The most complicated pattern of bifurcation transitions was obtained for small but finite Re_x values of the pumping along the x coordinate. In the absence of the pumping (Re_x = 0, Fig. 4a) or in the case of a weak pumping (Re_x =0.01, Fig. 4b) all instability modes are monotonic. The first oscillatory mode appears to the right of point BT₂ at Re_x ~ 0.113, then, at Re_x ~ 0.117, this mode goes over to the oscillatory instability mode of solution (2.1) AH₁, which remains most dangerous with further increase in Re_x.

Thus, the general pattern and the variety of bifurcations of the basic solutions are chiefly determined by the strength of pumping along the x direction corresponding to the longest side of the periodicity cell (l_x = 4π). In the case of weak pumping secondary stationary flows alternate, while at a stronger pumping self-oscillations occur; these can appear either as a result of the Andronov–Hopf bifurcation of the basic solution (2.1) at fairly large values of Re_x and the force amplitude λ or in the domain of their intermediate values, as a result of the breakup of the saddle-node homoclinic trajectory (SNIC bifurcation). Variants of the system dynamics listed above can be seen in Fig. 5. How general are these patterns, will be shown by the further calculations for other periodicity cells.

Fig. 5.

Characteristic dependences of the deviation from the stationary flow (2.1) δ on time: (a), perturbation behavior near the oscillatory instability threshold АH₁ for Re_x = 0.2 and Re_y = 0 (λ_cr ≅ 0.2, λ₀₁ = 2.1); λ = 2.1 corresponds to the oscillation decay and λ = 2.2 and 2.3 to the onset of the oscillatory secondary flow; (b), perturbation behavior near the threshold of monotonic instability В₁ at Re_x = 0.2, Re_y = 5 (λ_cr ≅ 7.074, λ_m1 = 23.5), λ = 23 corresponds to the perturbation decay and λ = 24 to the onset of a stationary secondary flow (logarithmic scale along the ordinate axis); (c), coexistence of three stable oscillatory states near the Bogdanov–Takens bifurcation at Re_x = 0.115 and Re_y =1 (λ_cr ≅ 1.006, ${{\lambda }_{{02}}}$ = 3.7705); and (d), oscillatory and stationary flows in the case of the SNIC bifurcation at Re_x = 0.115 and Re_y = 1 (λ_cr ≅ 1.006, ${{\lambda }_{{s1}}} = 6.3$).

4 DYNAMICS OF FLUID PARTICLES IN THE EULERIAN AND LAGRANGIAN REPRESENTATIONS

The system of equations (2.3) is written in the laboratory frame of reference, in the Eulerian coordinates attached to particular points of the physical space. The above-discussed dynamic states expressed in terms of these variables are either time-independent (main and secondary stationary flows) or are periodic functions of time (flows arisen in the process of the development of oscillatory instabilities). Observables corresponding to passive particles transported along streamlines and expressed in terms of Lagrangian variables show much richer dynamics.

The transport equations of these particles are as follows:

$$\frac{{dx}}{{dt}} = {{v}_{x}}(x,y,t);\quad \frac{{dy}}{{dt}} = {{v}_{y}}(x,y,t).$$

They were solved for the velocity field $({{v}_{x}},{\kern 1pt} \,{{v}_{y}})$ obtained by numerical integration of Eqs. (2.3). To visualize the Lagrangian dynamics the phase portraits were plotted in the coordinates $\left( {{{v}_{x}},{{v}_{y}},\Psi {\kern 1pt} '} \right)$.

The results presented below pertain to the case in which ${{l}_{x}} = 4\pi ,$ ${{l}_{y}} = 2\pi$, M = 20, and N = 20.

We begin with the time-independent velocity field. For any two-dimensional stationary flow of an incompressible fluid the equations of the Lagrangian dynamics are given by a conservative dynamic system with one degree of freedom in which the stream function plays the role of the Hamiltonian. The Lagrangian particle trajectories coincide with streamlines and in the case of the absence of stagnation points in a flow (which corresponds to λ < λ_cr for the ZPK96 flow (2.1)) the Lagrangian dynamics can be only periodic or quasiperiodic, depending on the rotation number ρ = Re_x/Re_y.

In both cases, the power spectrum of particle velocities is discrete [18]. At rational rotation numbers the torus surface is stratified into a continuum of closed streamlines repeatedly going round it: every fluid particle moves periodically, the motion period depending on a streamline. At irrational ρ the ergodicity takes place and every trajectory is dense on the torus.

At λ > λ_cr the streamline structure involves singular points and trajectories. For the periodicity cell measuring 2πm × 2πn these are 2mn saddle points and their separatrices confining 2mn vortices, i.e. zones of local flow containing each a stationary elliptic point surrounded by a continuum of closed streamlines. The trajectories of the points from the “global component” cannot penetrate into the vortices, while on the vortex boundaries the particle velocities slow down considerably near the saddle points (the time of flow around a vortex has a singularity of the logarithmic type). For this reason, the dynamics of the Lagrangian particles in the global component changes considerably. Since in the case of irrational rotation numbers the trajectories of the global component are dense everywhere in it, they return to the vicinities of the saddle points again and again and leave them again. The effect of repeated accelerations and decelerations is accumulated leading to qualitative changes. Although, due to the two-dimensional nature of the phase space, the Lagrangian particle trajectories cannot, be chaotic, they exhibit certain unusual properties, intermediate between laminar and turbulent flows. These are the singular-fractal nature of the power spectrum, a power-law decrease of the velocity correlations, and anomalies of the transport characteristics [12, 13].

Monotonic instabilities of the main flow (2.1) do not introduce qualitative variations into this pattern: similarly to the SNIC bifurcations, they generate new stable stationary velocity fields whereas any stationary flow, independently of the details of its structure, is, as before, characterized by the same rotation number ρ and can be decomposed into the global and localized components, while the Lagrangian observables in the case of an irrational ρ demonstrate decorrelation and a weak temporal unorderedness.

The changes induced by the oscillatory instability of the main flow are completely different in nature. As noted above, this instability can be observed in a wide parameter range, which leads to the onset of a time-dependent secondary flow (periodic in the Eulerian variables). The states born with a finite amplitude, as a result of the SNIC bifurcation, are also time-periodic. The phase space of a system governing the dynamics of a Lagrangian particle in a time-periodic plane velocity field is three-dimensional. Since the system conserves phase volume, its typical trajectories are exponentially unstable [19]. This phenomenon, that is, the chaotic dynamics of fluid particles in velocity fields having simple Eulerian properties, is known as the “Lagrangian chaos” or “chaotic advection” [20].

Below we restrict ourselves to the influence of the self-oscillatory nature of the flow on the general form of a Lagrangian trajectory, while its effect on the spectral and correlation characteristics of the Lagrangian particle velocity will be considered elsewhere.

The presence of chaotic streamlines leads to the mixing of phase trajectories which can penetrate (at λ > λ_cr) also in hitherto inaccessible regions with vortices. As before, the details of the process depend on whether the rotation number ρ is rational. Before the instability has appeared the phase space is two-dimensional and, in the case of rational ρ, represents a continuum of closed streamlines, characterized by a single rotation around the elliptic point in the flow component localized within the vortices and by many rotations around the whole torus in the global component. The appearance of the second temporal scale corresponding to the self-oscillation period in the Eulerian variables makes the phase space three-dimensional, while the continua of periodic orbits transform into the families of the Kolmogorov–Arnold–Moser tori (the so-named KAM tori) [21]. The newborn two-dimensional tori are embedded into each other and form an impermeable structure in the three-dimensional phase space: every fluid particle moves quasiperiodically along the surface of the corresponding torus, without being displaced across the structure. As the Eulerian self-oscillations enhance, the KAM tori start to break up, which leads to a gradual disappearance of barriers and an expansion of the part of the space accessible for any particle. Apparently, it is the tori lying near the saddle stagnation points that disintegrate first, which generates an initially weak mixing between the localized and global flow components. The breakup of the tori leads to chaotization of the motion. Initially, the Lagrangian chaos is not global: there exist a lot of chaotic components, which do not interact, since each of them is “pressed” between the KAM tori, which have not yet been destroyed. Certain components correspond to repeated (in accordance with the denominator of the rotation number) passages through the entire periodicity cell, whereas some other components contain weakly chaotized rotations within the former vortices. Gradually, the chaotic components merge and after the breakup of the last KAM torus the entire phase space opens up to all chaotic trajectories.

In the situation, where the rotation number is irrational, the pattern is somewhat different: here, after transition of the Eulerian variables to self-oscillations the continuum of the KAM tori appears only in the localized flow component. The chaotization of the main flow occurs only near the fixed saddle points, whose invariant manifolds are responsible for the geometry of mixing in the phase space [22]. As a result, with increase in λ the chaotic global trajectories penetrate increasingly deeper into the former inner regions of the vortices, where meanwhile the process of the breakup of the KAM tori takes place. Finally, the developed Lagrangiasn chaos occupies the entire phase space.

In the problem under consideration this general description of the Lagrangian chaos evolution with increase in the parameter holds true for sufficiently high values of the parameter Re_x: for example, at Re_у = 1, in the Re_x > 0.15 region. Al lower Re_x values the SNIC bifurcation interrupts abruptly the mechanism of gradual enlargement of the chaotic advection domain: the self-oscillations of the Eulerian variables cease and the system returns to the stationary velocity fields akin to those described above.

Figures 6 and 7 illustrate these transitions. At a rational ρ value the transition to the Lagrangian chaos occurs from the periodic solution (closed orbit on the torus) at λ < λ_cr, through a quasiperiodic state, and then to a new stationary flow after the SNIC bifurcation (Fig. 6), while for an irrational ρ it goes from a quasiperiodic flow at λ < λ_cr through a state with a singular-fractal spectrum (Fig. 7).

Fig. 6.

Variants of the Lagrangian dynamics at the rational rotation number ρ = 1/8: ${{l}_{x}} = 4\pi ;$ ${{l}_{y}} = 2\pi$, ${{\operatorname{Re} }_{x}} = 0.125,~$ ${{\operatorname{Re} }_{y}} = 1;$ ${{\lambda }_{{{\text{cr}}}}} = 1.008,$ ${{\lambda }_{{01}}} = {\text{ }}3.737,$ ${{\lambda }_{{s1}}} = {\text{ }}11.20$ (variant from Fig. 4e). The upper horizontal row presents the global trajectories of the Lagrangian particles initiated at the point (1,1); the second row presents the phase portraits of the global trajectories; the third row contains the particle trajectories starting near the center of a vortex; and the lower row presents the phase portraits for these trajectories. In the vertical columns the force amplitudes are as follows: λ = 3.7 (a), 3.8 (b), and 20 (c).

Fig. 7.

Variants of the Lagrangian dynamics at irrational rotation numbers (${{l}_{x}} = 4\pi ;$ ${{l}_{y}} = 2\pi$). The upper horizontal row presents the global trajectories of the Lagrangian particles; the second row presents the phase portraits of these trajectories for the following force amplitudes and initial points: (a), $~\lambda = 3.7$ (1, 1); (b), $\lambda = 3.7$ (6, 4); (c), $~\lambda = 3.728$ (1, 1); and (d) $\lambda = 3.728$ (6, 3.75); ${{\operatorname{Re} }_{x}} = (\sqrt 5 - 1){\kern 1pt} /{\kern 1pt} 2,~$ ${{\operatorname{Re} }_{y}} = 1;$ ${{\lambda }_{{{\text{cr}}}}} = 1.175,$ ${{\lambda }_{{m1}}} = {\text{ }}3.727$. The third and fourth rows (e, f, g, and h) present the variations of the phase portraits of the trajectories beginning near the center of the vortex with increase in the oscillation amplitude after the loss of the main solution stability at λ = λ₀: ${{R}_{x}} = 1,$ ${{\operatorname{R} }_{y}} = (\sqrt 5 - 1){\text{/}}2,$ ${{\lambda }_{{{\text{cr}}}}} = {\text{1}}{\text{.272}},$ ${{\lambda }_{0}} = {\text{2}}{\text{.712561}}$; (e), $\lambda = {{\lambda }_{0}} + {{10}^{{ - 4}}};$ ${{\lambda }_{0}} + {{10}^{{ - 3}}};$ ${{\lambda }_{0}} + {{10}^{{ - 2}}};$ (f), $\lambda = {{\lambda }_{0}} + {{10}^{{ - 4}}};$ (g), $\lambda = {{\lambda }_{0}} + 3 \times {{10}^{{ - 1}}};$ and (h), λ = ${{\lambda }_{0}} + 4 \times {{10}^{{ - 1}}}.$

Clearly, as the oscillation amplitude grows with increase in λ, the area of the “prohibited region” for a Lagrangian trajectory in the vicinities of the vortices decreases gradually and then this region vanishes. Earlier, it was tacitly assumed that instability starts in the presence of vortices. The onset of the Lagrangian chaos in the absence of vortices, which, as noted above, can be realized in a certain parameter domain (Re_x, Re_y), is different in nature: it corresponds to transition from a periodic or quasiperiodic flow pattern to the chaotic flows.

SUMMARY

Stability analysis of the family of time-independent spatially-periodic plane flows under consideration shows that generation of the hydrodynamic instability requires that the length of at least one side of the cavity includes several periods of the imposed spatial force. In a square cavity with the side length equal to the force period the basic flow remains stable in wide ranges of the external force amplitude and the pumping intensity. In extended cavities the instability generated at a sufficiently large external force can, depending on the mean fluid flow rates in two perpendicular directions, be monotonic or oscillatory. In the space of the constitutive parameters the state diagram is organized around the Bogdanov–Takens bifurcation, in which two eigenvalues of the linearization about the basic flow simultaneously vanish. The Lagrangian dynamics of passive particles transported by nonlinear secondary flows is determined by the absence or presence of the dependence of the Eulerian velocity field on time. Thus, as a result of repeated slow passages of the particles near stagnation points, the secondary stationary flows possess the same properties, as the basic flow, namely, long-range temporal correlations, the singularly continuous Fourier spectrum of the velocity, and anomalous transport. If the secondary flows in the Eulerian representation are time-periodic, then sufficiently large amplitudes of the external force lead to the breakup of the embedded KAM tori in the phase space of the problem and the establishment of chaotic advection (“Lagrangian chaos”) of the passive particles.

The generality of the results discussed is not restricted by the periodicity cell aspect ratio considered and the simple geometry of the imposed force. Within the framework of our approach calculation of analogous bifurcation diagrams is also possible for the cells with non-integer aspect ratios; the lengths can even be incommensurable. In order for secondary flows to be generated the length of at least one side must be greater than the spatial force periods (which are not obliged to coincide). If the force depends explicitly on the higher Fourier harmonics of the spatial coordinates, then the structure of the main stationary flow becomes more complicated; it contains vortices of different sizes. From the standpoint of the Lagrangian characteristics, that is, the power spectrum and the correlation functions of the tracer velocities, it is the ratio of the pumping intensities in the perpendicular directions, rather than the force geometry, that is important: at rational values of this ratio the spectra of all (!) stationary flows are discrete, while the correlations do not decay. Contrariwise, the irrationality of the pumping intensity ratio is the reason for the presence of a (singularly) continuous spectral component and the algebraic decay of correlations. In this connection, it should be noted that the transport anomalies accompanying the particle transport are enhanced by the stationary flow, if in its structure the vortices rotating clockwise and counterclockwise are disbalanced. For the unsteady flows developed in the course of oscillatory instabilities the quantitative characteristics depend, of course, on the imposed force geometry but the general pattern of transition to the Lagrangian chaos remains largely the same.