Oil reservoirs with a gas cap make up a significant proportion of gas and oil fields [1]. The extraction of oil from such fields has certain features and differs from the development of purely oil fields. Thus, a decrease in pressure in an area saturated with oil causes the boundary of the gas-oil contact to move. The movement of this interface can be unstable, which leads to gas breakthrough into the production well and the formation of immobile oil in the reservoir and near-wellbore region [2]. In other cases, instability and destruction of the gas-oil contact surface can cause flow fragmentation and the formation of residual immobile oil in the field [3]. Based on this, it can be concluded that the determining factor of many processes is the instability of filtration flows.

In recent years, analytical and numerical studies of the instability of interfaces during filtration in geothermal systems, soils, and rocks have been carried out [4–7]. In these works, the mathematical description of the filtration process in porous media was based on the Darcy’s law. It has been established that in many cases important for applications, the transition to instability occurs simultaneously for all values of the wave number or for infinitely large wave numbers. In the last case, the most rapidly growing mode of the unstable flow is the mode corresponding to an infinitely small linear size. Thus, we can conclude that the mathematical model based on the Darcy law is inapplicable for describing both the transition to instability itself and the subsequent development of the flow with the destruction of the interface, leading to the formation of “fingers.”

In [8], in the framework of the Darcy filtration theory, the stability of the gas-oil interface was studied under a pressure drop in an oil-saturated region. A criterion for the stability of the surface is found and it is shown that when the parameters change, the transition to the unstable regime occurs simultaneously for all wave numbers. It is natural to assume that the Darcy’s law, which describes well flows with a large characteristic length scale, cannot always give an adequate mathematical description of small-scale phenomena. In these cases, when studying filtration flows, instead of the Darcy law, it is proposed to use the Brinkman equation [9].

Interest in the Brinkman equation, as a generalized form of the Darcy filtration equation, arose largely as a result of attempts to formulate correct boundary conditions on the contact surface of a free fluid flow and a flow in a porous medium [10–12]. The properties of the Brinkman equation and boundary conditions on the contact surface of a free fluid and a porous medium were studied in [13, 14]. An analysis of the influence of inertial terms on the flow of a contacting free liquid and a liquid in a porous medium in the framework of the Brinkman equation is presented in [15]. In [16], the data of experiments on the stability of the interface between two miscible liquids, carried out for a vertical Hele–Shaw cell, are presented. A comparison was made with the results of studies of the linear stability of a flow subject to the Brinkman equation. In [17], the stability of a plane-parallel flow of a free fluid over a saturated porous medium was considered. A comparative analysis of the results using two approaches is given. In one case, the Brinkman model with Ochoa–Tapia–Whitaker boundary conditions was applied, and in the other case, the Darcy–Forchheimer equations with Beavers–Joseph boundary conditions were used.

The evolution of infinitely small and finite localized perturbations for a moving phase transition front was studied in [18, 19] in the Darcy approximation. The development of gravitational instability in a two-layer liquid of constant and variable viscosity in a porous medium was numerically studied in [20, 21] also using the Darcy law. The Brinkman equation was used in [22] to simulate the flow of a micropolar fluid in a porous medium.

In this paper, within the framework of the generalized Brinkman filtration equation, the stability of the gas-oil contact surface is studied with a decrease in pressure in the oil-saturated region.

1 PROBLEM FORMULATION

We consider the movement of oil in a porous medium for the case when a horizontal reservoir saturated with oil borders on top with a gas cap and on the bottom with a high permeability interlayer or fracture. It is assumed that the movement of oil is described by the generalized Brinkman filtration equation.

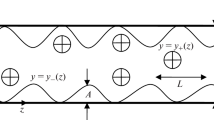
Let the lower boundary of the reservoir have a vertical Cartesian coordinate z = 0, and the upper boundary z = L. An infinite reservoir in the horizontal dimension includes the region Ωf, saturated with oil at 0 < z < S(x, t) and the region Ωg: S(x, t) < z < L, saturated with gas. We assume that the volume of the gas is large enough and its motion can be neglected, and the pressure in it is constant and equal to PG. We neglect the dissolution of gas in oil and the degassing of oil. When pumping oil from a highly permeable layer corresponding to the boundary z = 0, we assume that the pressure in it changes instantly throughout its entire length and is equal to a constant value of PF.

Oil is assumed to be incompressible, and its motion is described by the Brinkman equation, taking into account gravity

$$\text{div}\vec {V} = 0,$$
(1.1)
$$ - \nabla \left( {P + \rho gz} \right) + {{\mu }_{e}}\Delta \vec {V} - \frac{\mu }{k}\vec {V} = 0.$$
(1.2)

Here, P is the pressure, ρ the density, g the acceleration due to gravity, μ the dynamic viscosity, μe the effective dynamic viscosity, k the permeability, \({\kern 1pt} \vec {V}\) the filtration velocity vector.

Let us find the basic solution, which is supposed to be investigated for stability. We use the fluid incompressibility condition (1.1) and apply the divergence operation to equation (1.2). As a result, we obtain the Laplace equation for pressure

$$\Delta {\kern 1pt} P = 0.$$
(1.3)

If the surface of the oil and gas contact is flat and at time t has the z-coordinate H(t) > 0, then equation (1.3), as well as boundary conditions

$$P(x,0,t) = {{P}_{F}},$$
(1.4)
$$P(x,H(t),t) = {{P}_{G}}$$
(1.5)

satisfies the solution

$${{P}_{b}}(x,z,t) = \frac{{\left( {{{P}_{G}} - {{P}_{F}}} \right)z}}{{H(t)}} + {{P}_{F}},$$
(1.6)

From equation (1.2) we have

$${{V}_{{z,b}}}(x,z,t) = - \frac{k}{\mu }\left( {\frac{{{{P}_{G}} - {{P}_{F}}}}{{H(t)}} + \rho g} \right),$$
(1.7)
$${{V}_{{x,b}}}(x,z,t) = 0,$$
(1.8)

where Vx,b and Vz,b are x- and z-components of the velocity \({\kern 1pt} \vec {V}\) of the basic solution.

If we do not consider the processes of dissolution of gas in oil and degassing of oil, then the speed of the interface in the direction of the outer normal coincides with the normal component of the filtration rate \(\vec {V}(H(t))\), therefore, for the basic solution we obtain

$$\frac{{dH(t)}}{{dt}} = - \frac{k}{\mu }\left( {\frac{{{{P}_{G}} - {{P}_{F}}}}{{H(t)}} + \rho g} \right).$$
(1.9)

From (1.9) we have

$$t = \frac{\mu }{k}\left( {\frac{{{{P}_{G}} - {{P}_{F}}}}{{{{\rho }^{2}}{{g}^{2}}}}\ln \left( {\frac{{\rho g{{H}_{0}} + {{P}_{F}} - {{P}_{G}}}}{{\rho gH(t) + {{P}_{F}} - {{P}_{G}}}}} \right) - \frac{{H(t) - {{H}_{0}}}}{{\rho g}}} \right),$$
(1.10)

where H0 is the z-coordinate of the interface at t = 0. Relation (1.10) defines an implicit function H(t).

At the interface, the condition of equality of the normal stress components is satisfied, which has the form

$$P(x,s(x,t),t) - 2{{\mu }_{e}}\left( {\frac{\partial }{{\partial n}}{{V}_{n}}(x,z,t)} \right) = {{P}_{G}}.$$
(1.11)

Here, Vn is the normal velocity component to the surface S(x, t). \(\left( {\frac{{\partial {{V}_{n}}}}{{\partial n}}} \right)\) is the derivative of this component along the normal to the surface S(x, t).

The condition for shear stress, which is equal to zero (see, for example, [23]), can be written as

$$\frac{\partial }{{\partial n}}{{V}_{\tau }}(x,z,t) + \frac{\partial }{{\partial \tau }}{{V}_{n}}(x,z,t) = 0,$$
(1.12)

where Vτ is the tangent to the surface S(x, t) of the velocity \(\overrightarrow V \) component, \(\left( {\frac{\partial }{{\partial n}}{{V}_{\tau }}} \right)\) the derivative of this component in the direction of the normal, \(\left( {\frac{\partial }{{\partial \tau }}{{V}_{n}}} \right)\) the derivative of the normal velocity component in the direction of the tangent.

2 DERIVATION OF THE DISPERSION EQUATION

In the framework of the linear approach, the unknown functions can be represented as

$$S(x,t) = H(t) + s(x,t),$$
(2.1)
$$P(x,z,t) = {{P}_{b}}(x,z,t) + p(x,z,t),$$
(2.2)
$${{V}_{x}}(x,z,t) = u(x,z,t),$$
(2.3)
$${{V}_{z}}(x,z,t) = {{V}_{{z,b}}}(x,z,t) + {v}(x,z,t),$$
(2.4)

where p(x, z, t), u(x, z, t), \({v}\)(x, z, t), s(x, t) are the small perturbations of the pressure, horizontal and vertical velocity components, as well as the position of the oil-gas interface, respectively.

Since equation (1.3) is linear, p(x, z, t) satisfies the equation

$$\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}p(x,z,t) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}p(x,z,t) = 0.$$
(2.5)

We will look for a solution for p(x, z, t) in the form

$$p(x,z,t) = \Pi (z)f(t)\exp (iKx),$$

then from equation (2.5) we obtain

$$ - {{K}^{2}}\Pi (z) + \frac{{{{d}^{2}}}}{{d{{z}^{2}}}}\Pi (z) = 0.$$
(2.6)

We write the general solution of equation (2.6) in the form

$$\Pi (z) = {{C}_{1}}\exp (Kz) + {{C}_{2}}\exp ( - Kz).$$
(2.7)

Taking into account that perturbations arise on the free surface and decay at the lower boundary of the low-permeability layer, the second term on the right side of expression (2.8) can be neglected, then

$$\Pi (z) = {{C}_{1}}\exp (Kz).$$
(2.8)

Solutions for u(x, z, t) and \({v}\)(x, z, t) we will search in the form

$$u(x,z,t) = U(z)f(t)\exp (iKx),$$
(2.9)
$${v}(x,z,t) = V(z)f(t)\exp (iKx).$$
(2.10)

Substituting (2.2), (2.3), and (2.4) in equation (1.2), and using (2.9), (2.10), (2.11) we have

$$U(z) = - ic{{C}_{1}}K{{e}^{{Kz}}} - {{K}^{2}}U(z){{m}_{e}} + \left( {\frac{{{{d}^{2}}}}{{d{{z}^{2}}}}U(z)} \right){{m}_{e}},$$
(2.11)
$$V(z) = - c{{C}_{1}}K{{e}^{{Kz}}} - {{K}^{2}}V(z){{m}_{e}} + \left( {\frac{{{{d}^{2}}}}{{d{{z}^{2}}}}V(z)} \right){{m}_{e}},$$
(2.12)

where \(c = k{\text{/}}\mu \),\({{m}_{e}} = c{{\mu }_{e}}\).

For the general solution of equation (2.12)

$$U(z) = - ic{{C}_{1}}K\exp (Kz) + {{C}_{3}}\exp ( - \sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z) + {{C}_{4}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z)$$

and for the sufficiently large oil-bearing reservoir thickness, we can neglect the term on the right-hand side, which decreases with increasing z, and write the solution in the form

$$U(z) = - ic{{C}_{1}}K\exp (Kz) + {{C}_{u}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z).$$
(2.13)

Similarly, from equation (2.13) we have

$$V(z) = - c{{C}_{1}}K\exp (Kz) + {{C}_{{v}}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z).$$
(2.14)

It follows from the liquid phase incompressibility condition (1.1) that

$$\frac{\partial }{{\partial x}}u(x,z,t) + \frac{\partial }{{\partial z}}{v}(x,z,t) = 0.$$
(2.15)

Using relations (2.10) and (2.11), from equation (2.16) we obtain

$$iKU(z) + \frac{d}{{dz}}V(z) = 0.$$
(2.16)

Substituting (2.14) and (2.15) into equation (2.17), we find an equation relating the coefficients Cu and \({{C}_{{v}}}\)

$$i{{C}_{u}}K\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z) + {{C}_{{v}}}\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} \exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} z) = 0.$$
(2.17)

From (2.18) we get

$${{C}_{u}} = i\frac{{\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} }}{K}{{C}_{{v}}}$$
(2.18)

We assume that perturbation of the front position has the form

$$s(x,t) = {{C}_{\eta }}f(t){{e}^{{iKx}}}$$
(2.19)

and ∂s/∂x ≪ 1. Then, within the linear approach from (1.11) follows

$$\begin{gathered} {{C}_{1}}(2{{K}^{2}} + 1{\text{/}}{{m}_{e}})\exp (KH(t)) + {{C}_{\eta }}\frac{{{{P}_{G}} - {{P}_{F}}}}{H} \\ - \;{{C}_{{v}}}\frac{{2\sqrt {{{m}_{e}}} }}{c}\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} \exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t)) = 0. \\ \end{gathered} $$
(2.20)

Thus, the normal velocity of the interface can be found from equation

$${{C}_{{v}}}\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t)) - c{{C}_{1}}K\exp (KH(t)) - {{C}_{\eta }}\frac{{f{\kern 1pt} '(t)}}{{f(t)}} = 0.$$
(2.21)

From (1.12) in the framework of linear approach we have

$$\frac{\partial }{{\partial z}}u(x,z,t) + \frac{\partial }{{\partial x}}{v}(x,z,t) = 0.$$
(2.22)

Using relations (2.14), (2.15), and (2.19), we transform equation (2.23) to the form

$$\left( {\frac{i}{K}({{K}^{2}} + 1{\text{/}}{{m}_{e}}) + iK} \right)\exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t)){{C}_{{v}}} - 2ic{{C}_{1}}{{K}^{2}}\exp (KH(t)) = 0.$$
(2.23)

and obtain homogeneous system of equations (2.21), (2.22), (2.24) for the unknown parameters C1, \({{C}_{{v}}}\), Cη. The system has a non-trivial solution if the determinant of the matrix coefficients is zero

$$Det \equiv \left| {\begin{array}{*{20}{c}} {(2{{K}^{2}} + 1){{e}_{k}}}&{ - \frac{4}{c}\sqrt {{{m}_{e}}} {{f}_{k}}{{e}_{H}}}&{\frac{{{{P}_{G}} - {{P}_{F}}}}{{H(t)}}} \\ { - cK{{e}_{k}}}&{{{e}_{H}}}&{ - \frac{{f{\kern 1pt} '(t)}}{{f(t)}}} \\ { - 2ic{{e}_{k}}{{K}^{2}}}&{\frac{{if_{k}^{2}{{e}_{H}}}}{{{{m}_{e}}K}} + iK{{e}_{H}}}&0 \end{array}} \right| = 0.$$
(2.24)

Here, \({{e}_{H}} = \exp (\sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} H(t))\), \({{e}_{K}} = \exp \left( {KH(t)} \right)\), \({{f}_{k}} = \sqrt {{{K}^{2}} + 1{\text{/}}{{m}_{e}}} \).

From (2.25) we obtain

$$\frac{{f{\kern 1pt} '(t)}}{{f(t)}} = - \frac{{Kc({{P}_{G}} - {{P}_{F}})({{K}^{2}}{{m}_{e}} - {{f}_{k}})}}{{H(t)(2{{K}^{4}}m_{e}^{2} - 4{{k}^{3}}m_{e}^{{3/2}}{{f}_{k}} + 2{{K}^{2}}f_{k}^{2}{{m}_{e}} + {{K}^{2}}{{m}_{e}} + f_{k}^{2})}}$$

or

$$\frac{{f{\kern 1pt} '(t)}}{{f(t)}} = \frac{{Kc({{P}_{G}} - {{P}_{F}})}}{{H(t)(2{{K}^{4}}m_{e}^{2} - 4{{k}^{3}}m_{e}^{{3/2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} + 2{{K}^{2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} \,{{m}_{e}} + 2{{K}^{2}}{{m}_{e}} + 1)}}.$$
(2.25)

3 INVESTIGATION OF FLOW STABILITY

Within the Darcy approximation the effective viscosity μe is equal to zero, respectively me = 0, then from (2.26) we have

$$\frac{{f{\kern 1pt} '(t)}}{{f(t)}} = \frac{{Kc\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{{H(t)}}.$$
(3.1)

The condition for the unstable development of perturbations at the interface, which follows from relation (3.1), coincides with the condition obtained using the Darcy law [6, 7]. In the case of instability, when PG > PF, the perturbation amplitude tends to infinity with the growth of the wave number K → ∞.

Consider the behavior\(f{\kern 1pt} '(t)\) at K → ∞, when me ≠ 0. From (2.25) we have

$$\frac{{f{\kern 1pt} '(t)}}{{f(t)}} \approx \frac{{c\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{{2{{m}_{e}}H(t)K}}.$$
(3.2)

Therefore, in the Brinkman approximation, the rate of damping or growth of short-wave disturbances tends to zero at K → ∞ both in the stable (PF > PG) and in the unstable (PF < PG) case.

If we use the quasi-stationary condition, which follows from the fact that the characteristic time of motion of the gas-oil interface is much greater than the characteristic time of pressure redistribution, then we can neglect the dependence of H on t on the right side of the equation (2.25) and assume that the interface is fixed. Similar conditions of quasi-stationarity are valid for many problems of filtration theory with discontinuity surfaces [3, 24]. Then we have

$$f(t) = \exp (\sigma t).$$

And relations (2.25), (3.1), and (3.2) have the forms

$$\sigma = \frac{{Kc({{P}_{G}} - {{P}_{F}})}}{{H(2{{K}^{4}}m_{e}^{2} - 4{{k}^{3}}m_{e}^{{3/2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} + 2{{K}^{2}}\sqrt {{{K}^{2}}{{m}_{e}} + 1} {\kern 1pt} \,{{m}_{e}} + 2{{K}^{2}}{{m}_{e}} + 1)}},$$
(3.3)
$$\sigma = \frac{{Kc\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{H}$$
(3.4)
$$\sigma \approx \frac{{c\left( {{{P}_{G}} - {{P}_{F}}} \right)}}{{2{{m}_{e}}HK}}.$$

In Fig. 1, we demonstrate the dispersion curve Σ = Σ (K) that follows from (3.3), where dimensionless parameter \(\Sigma = \frac{{\sigma H\sqrt {{{m}_{e}}} }}{{c{{P}_{k}}}}\) depends on dimensionless wave number \(\kappa = K\sqrt {{{m}_{e}}} \) and Pk = PG – PF. It is seen that Видно, that the perturbation growth rate has a maximum, which is reached at \(K\sqrt {{{m}_{e}}} \approx 0.72\) and tends to zero with an increase in the wavenumber K → ∞.

Fig. 1.
figure 1

Dimensionless growth rates Σ versus dimensionless wave number κ, here Pk = PG – PF.

Full size image

In Fig. 2 the dimensionless perturbation growth rates for small dimensionless wave numbers is compared for the Darcy (curve 1) and Brinkman (curve 2) filtration equations. At \(K\sqrt {{{m}_{e}}} \) ≪ 1 the Darcy equation describes well the behavior of a physical system, and for large wave numbers, the error from using the Darcy law becomes significant. It follows from (3.3) that since the expression in the denominator is always positive, the transition to instability occurs when the sign of the difference between the pressure in the gas cap PG and the pressure in the high-permeability layer PF changes.

Fig. 2.
figure 2

Dimensionless growth rates Σ versus dimensionless wave number κ: 1, Darcy’s law; 2, Brinkman’s law.

Full size image

In Fig. 3 we illustrate the change in the dimensionless parameter  \(\frac{{\sigma H\sqrt {{{m}_{e}}} }}{{c{{P}_{k}}}}\), which describes the growth or decay of the perturbations, on dimensionless wave number \(K\sqrt {{{m}_{e}}} \) at fixed PG and different values of PF. It can be seen that the transition to instability occurs at PG = PF simultaneously for all values of the wave number.

Fig. 3.
figure 3

Dimensionless growth rates Σ versus dimensionless wave number κ: 1–6 – PF = (0.8, 0.9, 0.99, 1.01, 1.1, 1.2) PG.

Full size image

SUMMARY

The dynamics and stability of vertical flow in an oil reservoir with a gas cap has been studied. The oil flow was described by the generalized Brinkman filtration equation. The law of motion of a flat horizontal interface between oil and gas is presented. The normal mode method is used to study the flow stability with respect to infinitesimal perturbations of a flat boundary. It is shown that such perturbations increase if the pressure in the gas cap is higher than the pressure in the high-permeability formation from which oil is produced. If the flat interface is at rest, then the pressure in the gas cap is less than in the high-permeability layer, which is equal to the hydrostatic pressure. At the first stage of pressure reduction in the interlayer, the contact surface will begin to move downward, but will remain stable until the pressure in the interlayer drops below the pressure in the gas cap. After that, the movement of the oil-gas border will become unstable. In this case, nonlinear instability takes place for any wavelength, but depends on the wave number K in such a way that for K → ∞ and K → 0 this rate tends to zero. There is a certain value of the wave number at which the growth rate has a maximum.

When using Darcy’s law, instability also occurs if the pressure in the gas cap is greater than the pressure in the interlayer. However, in this case, the growth rate of the perturbation increases indefinitely with the decreasing perturbation wavelength. In this case, short-wave perturbations grow arbitrarily fast, which does not allow obtaining a reliable picture of the flow and indicates the inapplicability of the mathematical model based on the Darcy law to describe both the transition to instability itself and the subsequent development of the flow with the destruction of the interface, leading to the formation of fingers. The use of the generalized Brinkman filtration equation makes it possible to eliminate the anomalous nature of the evolution of short-wave disturbances, which opens up the possibility of studying problems ill-posed in terms of the Darcy approach.

The work was carried out with support from the Russian Science Foundation under the grant no. 21-11-00126.