One of the major problems of creation of the scramjet engines is to organize stable combustion of fuel components in supersonic streams and ensure the completeness of combustion and the effectiveness of heat transfer to air flow at finite distances from the fuel injectors to the combustor exit [1, 2].

The laws of conducting the thermogasdynamic and combustion processes in supersonic air flow combustors are studied during more than 50 years. Several schemes of organizing combustion in supersonic flows are known. Among these schemes we can mention combustion in cavities on the combustion chamber walls that showed its effectiveness. In one of the first complex studies devoted to the experimental and computational investigation of scramjet chambers with the flameholder in form of a cavity [3–6], the possibility of implementation of the sub- and supersonic combustion regimes in the same combustion chamber in hydrogen injection from pylons and surface was demonstrated experimentally.

In [3] the results of the experimental investigation of work processes in the uncooled combustion chamber of dual mode scramjet with hydrogen fuel at sub- and supersonic velocities are given. The investigation was carried out on the test stand in which the velocity at the combustion chamber inlet М = 2, the total temperature Т0 = 750–950 K, and the total pressure Р0 = 0.2–0.3 MPa were ensured. Hydrogen was injected from four rows of injectors located on a pylon ahead of the first flameholder, on the lower and upper surfaces of the combustion chamber ahead of the first and second flameholders, as well as between them. The pressure distributions and the densities of convective heat fluxes amounted to \({{q}_{w}}\) ~ 20–100 W/cm2 were measured on the upper and lower surfaces. The thermogasdynamic parameter distributions along the channel, the completeness of combustion of hydrogen-air mixture, the features of combustion stabilization, the data on heat transfer and conditions of interaction of the air intake and the combustion chamber were discussed.

In [4] an axisymmetric scramjet, similar to [3], aimed at operation under the flight conditions corresponding to М ~ 6, was numerically investigated. In addition to studying the thermogasdynamic flow structure, an important result of that investigation is the computational estimate of the densities of convective heat fluxes on the surfaces of structural elements. Two flameholders and three rows of atomizers for hydrogen injection, two located inside the flameholders of trapezoidal shape, were designed in the combustion chamber construction. The calculations were carried out using two author’s computer codes whose results showed rational agreement. The initial data corresponded to flight at the altitude of 26 km at М = 6.5. The reacting mixture of air and hydrogen was assumed to be in the stoichiometric relationship. The fuel was injected at the pressure of 0.560 MPa and the temperature of 960 K. Note a fairly high level of convective heat fluxes towards the wall. The density of convective heat fluxes reached ~70 W/cm2 on the surface of the external compression diffuser. The density of convective heat fluxes reached 175 W/cm2 on the central body inside the air intake (internal part of the external compression diffuser), although this quantity was equal to 40 W/cm2 on the external surface. The maximum density of convective heat fluxes (230 W/cm2) was reached in the neighborhood of the first flameholder at which hydrogen was injected.

In [5, 6] the information obtained as a result of flight tests of a similar combustion chamber and computational interpretation of the operation conditions of the propulsion unit was given.

In [7] kerosene ignition and flameholding in the two-dimensional scramjet combustion chamber were investigated experimentally. The scramjet operation on kerosene fuel was demonstrated at the free-stream Mach number equal to 6. Hydrogen injection from pylons was used for kerosene ignition and flameholding. The conditions at which kerosene combustion was maintained after termination of hydrogen injection were found.

In [8] the thermogasdynamic processes in the model combustion chamber of a dual-mode scramjet with the flameholder of trapezoidal shape were carried out experimentally. A withdrawable butterfly valve aimed at backpressure controlling in the gasdynamic channel was located ahead of exit to the nozzle block at the end of combustion chamber. 15 atomizers (only 13 of them were in operation), of 0.078 cm in diameter and spaced at 0.95 cm, were located on the inclined internal surface of the cavity. The cavity width was equal to approximately 15 cm. The combustible mixture was injected at the sonic speed. Temperature probes and a spark combustion trigger were located on the lower cavity bottom. The investigation of the time-dependent flow structure in the combustion chamber without fuel injection and with ethylene and JP-7 kerosene injection when the butterfly valve height was varied was a practically important experimental result of [8]. The following phenomena were studied experimentally: the effect of the pressure on the gas temperature in cavity (the pressure was varied due to change in the height of rising the butterfly valve), the influence of an additional injection of fuel components in the direction normal to the upper surface at a distance of 2 cm from the leading boundary of cavity (the structure and position of atomizers were similar to those located inside the cavity), the influence of the Mach number at inlet to insulator, and the effect of JP-7 kerosene injection instead of ethylene.

An analysis of the results of [8] and other studies on supersonic flow past trapezoidal cavities [9–11] in channels showed the high sensitivity of the gas dynamics and combustion characteristics to the large number of initial data, such as the mainstream velocity and pressure in the channel, the dimensions and shapes of flameholders, the location of atomizers and the characteristics of injected fuel compositions. It was shown that there is a significant influence of various gas stream control methods in form of butterfly valves or air injection to the gas stream on the flow field structure [12, 13].

As a whole, the concept of using the flameholders in form of cavities showed its prospectivity. There are examples of using similar flameholders in solid-fuel scramjet demonstrators [14]. One must admit that the use of the concept of flameholders in form of cavities in the scientific program of bench scale and flight tests HIFiRE-2 [15, 16] was successful.

The extensive test data obtained experimentally underlay the large number of computational investigations. In [17], devoted to analysis of the experimental data of bench scale tests of supersonic combustion chambers, a separate section was devoted just to thermogasdynamics of supersonic flows in channels with cavities. Among many studies, we note the most interesting ones in connection with the aims of the present work. These works can be divided into several groups, namely, the methods and results of the numerical simulation of gasdynamic processes of a wide class of steady-state and pulsed combustion schemes and the study of the laws of shock wave/boundary layer interaction since such a form of interaction is one of the important interactions in supersonic combustion chambers. Many works are devoted to the investigation of the chemical kinetics models used in thermogasdynamic calculations. The problem of organizing the triggering and ensuring the completeness of combustion in the scramjet chambers is extremely important; therefore, in many studies just these problems were discussed in detail.

The problem of ensuring the thermal regime in combustion chambers is of large practical significance. An extensive spectrum of models is used in the investigations, namely, from the integral models based on the thermodynamic cycles [18] and two-dimensional thermogasdynamic models of mean productivity [19] to the three-dimensional combustion models based on the Navier–Stokes equations [20], the Reynolds-averaged Navier–Stokes equations [21], and the limiting presently available hybrid RANS/LES-models of gas dynamics with combustion of fuel compositions [22]. In [23] it was attempted to simulate a small section of combustion chamber with the use of the DNS model. The direction of development of the numerical models for studying the phenomenon of off-design operation of the combustion chamber [24] also seems to be important.

It is necessary to make a general remark with respect to using some or other computational models. This remark consists in the fact that, undoubtedly, the use of the most complex computational models and algorithms favors to progress in this field but does not warrant obtaining of the most reliable data. This means that the simplified models have a smaller value as compared with the extremely detailed models to clarify the general laws of the thermogasdynamic processes under consideration.

Note that, even without regard to the processes of combustion, gas dynamics of channels with cavities attracted considerable attention of investigators. Mainly, this relates to the phenomena, fairly interesting for fundamental liquid and gas mechanics, of the development of gasdynamic fluctuations generated by the interaction of the main supersonic stream with vortex flows within the cavities in flow [10]. Organizing of combustion in cavities makes it possible to stabilize the thermal extraction zone in average, although the processes of combustion and flow are time-dependent.

The majority of the works on supersonic combustion in the combustion chambers are devoted to the experimental and computational studying of the gasdynamic processes and laws of ignition and combustion. Substantially lesser number of works is devoted to analysis of convective and, in particular, radiative heating of the combustion chamber walls. This has important practical value in analyzing the propulsion heat balance. Among the studies which are especially devoted to analysis of the densities of convective and radiative heat fluxes, we can note [3, 4, 25–29]. In the studies cited above it was noted that the density of convective heat fluxes on the flameholder and combustion chamber walls can reach the value of the order of 200 W/cm2 and of radiative heat fluxes of the order of 20 W/cm2. However, it should be borne in mind that radiative heating of the chamber walls depends considerably on the radiating volume dimensions, i.e., has the volumetric nature. In any case, the noted level of expected densities of convective and radiative heat fluxes points to the necessity of solving the problems of thermal protection shield in the scramjet chambers.

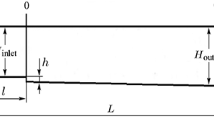
In the present study several regimes of supersonic ethylene combustion in the model scramjet combustion chamber are investigated numerically. In Fig. 1 we have reproduced the computational scheme. The initial data for calculations, including the gasdynamic channel geometry and the flow conditions, are borrowed from [8]. As noted above, despite the apparent simplicity of implementation of the required combustion regimes in dual-mode combustion chambers, the number of the specified parameters and the extent of their influence on the thermogasdynamic processes turn out to be so large that up to present time there is no unified theory that makes it possible to carry out prediction and detailed numerical description of the variety of thermogasdynamic calculations. As judged by the literature cited, the experimental and computational investigations are continued. This relates to scramjet chamber of the type [8] studied in the present paper.

Fig. 1.
figure 1

Diagram of combustion chamber (a) and computational grid ((b) each fourth coordinate line is shown). Arrows show the directions of main air flow (7) and two combustible mixture injection zones (8 and 9).

Full size image

The present investigation is carried out within the framework of the complete radiative-gasdynamic formulation of the thermodynamic processes in the dual-mode scramjet combustion chamber with the flameholder in form of a trapezoidal cavity when these processes accompany ethylene combustion in air. As in [8], various heights of rising the butterfly valve are taken into account. In the course of solving the radiative-gasdynamic problem, the densities of convective, spectral, and integral radiative heat fluxes toward the combustion chamber walls are determined, the influence of the air stream pressure in the inlet device duct on the intensity of convective and radiative heating is analyzed, and the structure of the unsteady self-oscillation regime of ethylene combustion under various conditions is studied. The total forces exerted on the internal surface of combustion chamber are determined for all the variants calculated.

1 COMPUTATIONAL MODEL

The NERAT-2D author’s computer program [30] which implements numerical integration of the system of mechanics equations for a viscous heat-conducting chemically reacting and selectively radiating gas was used for numerical simulation. In each time step, the following system of continuity, Navier-Stokes, and energy conservation equations, as well as the mass conservation equations for chemical species and the chemical kinetics and selective thermal radiation transfer equations, was successively integrated:

$$\frac{{\partial \rho }}{{\partial t}} + {\text{div}}\left( {\rho {\mathbf{V}}} \right) = 0,$$
(1.1)
$$\frac{{\partial \rho u}}{{\partial t}} + {\text{div}}\left( {\rho u{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial x}} - \frac{2}{3}\frac{\partial }{{\partial x}}\left( {\mu {\text{div}}{\mathbf{V}}} \right) + \frac{\partial }{{\partial y}}\left[ {\mu \left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + 2\frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right),$$
(1.2)
$$\frac{{\partial \rho {v}}}{{\partial t}} + {\text{div}}\left( {\rho {v}{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial y}} - \frac{2}{3}\frac{\partial }{{\partial y}}\left( {\mu {\text{div}}{\mathbf{V}}} \right) + \frac{\partial }{{\partial x}}\left[ {\mu \,\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + 2\frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial {v}}}{{\partial y}}} \right),$$
(1.3)
$$\rho {{c}_{p}}\frac{{\partial T}}{{\partial t}} + \rho {{c}_{p}}{\mathbf{V}}\operatorname{grad} T = \operatorname{div} \left( {\lambda \operatorname{grad} T} \right) + \frac{{\partial p}}{{\partial t}} + {\mathbf{V}}\operatorname{grad} p + {{\Phi }_{\mu }} - {{Q}_{{V,R}}}$$
(1.4)
$$ - \;\sum\limits_{i = 1}^{{{N}_{s}}} {{{h}_{i}}{{{\dot {w}}}_{i}}} + \sum\limits_{i = 1}^{{{N}_{s}}} {\rho {{c}_{{p,i}}}{{D}_{i}}} \left( {\operatorname{grad} {{Y}_{i}} \times \operatorname{grad} T} \right),$$
$$\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + \operatorname{div} {{\rho }_{i}}{\mathbf{V}} = - \operatorname{div} {{{\mathbf{J}}}_{i}} + {{\dot {w}}_{i}},\quad i = 1,\;2,\; \ldots ,\;{{N}_{s}},$$
(1.5)
$${{\left( {\frac{{{\text{d}}{{X}_{i}}}}{{{\text{d}}t}}} \right)}_{n}} = ({{b}_{{i,n}}} - {{a}_{{i,n}}}){{K}_{n}}\prod\limits_j^{{{N}_{s}}} {X_{j}^{{{{a}_{{j,n}}}}}} ,\quad i,j = 1,\;2,\; \ldots ,\;{{N}_{s}};\quad n = 1,\;2,\; \ldots ,\;{{N}_{r}},$$
(1.6)
$$\boldsymbol{\Omega} \frac{{\partial {{J}_{\omega }}\left( {{\mathbf{r}},\boldsymbol{\Omega} } \right)}}{{\partial {\mathbf{r}}}} + {{\kappa }_{\omega }}\left( {\mathbf{r}} \right){{J}_{\omega }}\left( {{\mathbf{r}},\Omega } \right) = {{\kappa }_{\omega }}\left( {\mathbf{r}} \right){{J}_{{b,\omega }}}\left( {\mathbf{r}} \right),$$
(1.7)

where t is time, r is the radius-vector of a point in space at which the spectral radiation intensity is determined, Ω is the unit vector of the direction of propagation of radiation, \({{\kappa }_{\omega }}({\mathbf{r}})\), \({{J}_{\omega }}\left( {{\mathbf{r}},{\boldsymbol{\Omega }}} \right)\), and \({{J}_{{b,\omega }}}\left( {\mathbf{r}} \right)\) are spectral absorption coefficient, the intensity of radiation of the medium and the perfectly black body, respectively, \({\mathbf{V}} = {\mathbf{i}}u + {\mathbf{j}}{v}\) is the velocity, u and \({v}\) are the velocity components along the axes х and у of the Cartesian coordinate system, p and \(\rho \) are the pressure and the density, respectively, Т is the temperature, \({{Q}_{{V,R}}}\) are the volume energy losses due to thermal radiation (under certain conditions, in this case thermal -radiation reabsorption turns out to be of importance);

$${{\Phi }_{\mu }} = \mu \left[ {2{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}} + } \right.\left. {{{{\left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)}}^{2}} - \frac{2}{3}{{{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}}} \right)}}^{2}}} \right]$$

is the dissipation function, \(\mu \) and \(\lambda \) are the viscosity and thermal conductivity coefficients, respectively, cp is the specific heat of the gas mixture, Ns is the number of components of the gas mixture, \({{Y}_{i}} = \frac{{{{\rho }_{i}}}}{\rho }\) is the relative mass number density of the ith component, \({{c}_{{p,i}}}\) and \({{h}_{i}}\) are the specific heat at constant pressure and the specific enthalpy of the ith component, \({{\rho }_{i}}\) and \({{{\mathbf{J}}}_{i}}\) are the density and the density of flux of the ith component, respectively, \({{{\mathbf{J}}}_{i}} = - \rho {{D}_{i}}\operatorname{grad} {{Y}_{i}}\), \({{D}_{i}}\) is the effective diffusion coefficient of the ith component, \({{X}_{i}} = {{{{\rho }_{i}}} \mathord{\left/ {\vphantom {{{{\rho }_{i}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}\) and \({{M}_{i}}\) are the volume-molar number density and the molecular weight of the ith component, \({{K}_{n}}\) are the global reaction rate constants, \({{a}_{{j,n}}}\) and \({{b}_{{j,n}}}\) are the stoichiometric coefficients, \({{N}_{r}}\) is the number of chemical reactions, and \({{\dot {w}}_{i}}\) is the mass rate of formation of the ith component in each elementary volume of the computational domain:

$${{\dot {w}}_{i}} = \sum\limits_{n = 1}^{{{N}_{r}}} {{{M}_{i}}{{{\left( {\frac{{d{{X}_{i}}}}{{dt}}} \right)}}_{n}}} .$$

In order to integrate numerically the system of equations, we use a series of closing relations among which, above all, we can mention the thermal and caloric equations of state of the gas mixture:

$$p = \rho \frac{{{{R}_{0}}}}{{{{M}_{\Sigma }}}}T,\quad {{c}_{p}} = \sum\limits_i^{{{N}_{s}}} {{{Y}_{i}}{{c}_{{p,i}}}} ,$$
(1.8)

where \({{R}_{0}}\) is the universal gas constant and \({{M}_{\Sigma }} = {{\left( {\sum\limits_i^{{{N}_{s}}} {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}} } \right)}^{{ - 1}}}\) is the molecular weight of the gas mixture.

The specific heat were calculated using the following approximation relations for the corresponding molar functions:

$${{h}_{i}} = \chi T\left( {\frac{{d{{G}_{i}}}}{{d\chi }}} \right) + {{\varphi }_{{8,i}}} \times {{10}^{3}},\,\,{\text{J/mol}},$$
$${{c}_{{p,i}}} = 2\chi \left( {\frac{{d{{G}_{i}}}}{{d\chi }}} \right) + {{\chi }^{2}}\left( {\frac{{{{d}^{2}}{{G}_{i}}}}{{d{{\chi }^{2}}}}} \right),\,\,{\text{J/molK}},$$

where \({{\varphi }_{{l,i}}}\), \(l = 1,\; \ldots ,\;8\), are the approximation coefficients [31] from the total thermodynamic potential

$${{G}_{i}} = {{\varphi }_{{1,i}}} + {{\varphi }_{{2,i}}}\ln \chi + {{\varphi }_{{3,i}}}{{\chi }^{{ - 2}}} + {{\varphi }_{{4,i}}}{{\chi }^{{ - 1}}} + {{\varphi }_{{5,i}}}\chi + {{\varphi }_{{6,i}}}{{\chi }^{2}} + {{\varphi }_{{7,i}}}{{\chi }^{3}},\quad \chi = T \times {{10}^{{ - 4}}},$$

and \({{\varphi }_{{{\kern 1pt} {\kern 1pt} 8,i}}}\) is the ith component formation energy under the standard conditions.

The global reaction rate constants

$${{K}_{n}} = {{A}_{n}}{{T}^{m}}\exp ( - {{T}_{a}}{\text{/}}T)$$

were determined using the kinetic ethylene combustion model [21].

The viscosity and thermal conductivity coefficients of gas mixtures, as well as the diffusion coefficient, were calculated from the following combinatorial formulas [32] for the viscosity, thermal conductivity, and binary diffusion coefficients of individual components obtained in the first approximation of the Chapman–Enskog theory:

$$\mu = \frac{1}{{\sum\limits_{i = 1}^{{{N}_{c}}} {\left( {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{\mu }_{i}}}}} \right. \kern-0em} {{{\mu }_{i}}}}} \right)} }},\quad \lambda = 0.5\left[ {\sum\limits_{i = 1}^{{{N}_{c}}} {{{x}_{i}}{{\lambda }_{i}}} + \frac{1}{{\sum\limits_{i = 1}^{{{N}_{c}}} {\left( {{{{{x}_{i}}} \mathord{\left/ {\vphantom {{{{x}_{i}}} {{{\lambda }_{i}}}}} \right. \kern-0em} {{{\lambda }_{i}}}}} \right)} }}} \right],\quad {{D}_{i}} = \frac{{1 - {{x}_{i}}}}{{\sum\limits_{j \ne i}^{{{N}_{c}}} {\left( {{{{{x}_{j}}} \mathord{\left/ {\vphantom {{{{x}_{j}}} {{{D}_{{ij}}}}}} \right. \kern-0em} {{{D}_{{ij}}}}}} \right)} }},$$
$${{\mu }_{i}} = 2.67 \times {{10}^{{ - 5}}}\frac{{\sqrt {{{M}_{i}}T} }}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2) * }}}},\,\,{\text{g/cm}}\;{\text{s,}}$$
$${{\lambda }_{i}} = 8330\sqrt {\frac{T}{{{{M}_{i}}}}} \frac{1}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2) * }}}},\,\,{\text{erg/cm}}\;{\text{K}},$$
$${{D}_{{i,j}}} = 1.858 \times {{10}^{{ - 3}}}\sqrt {{{T}^{3}}\frac{{{{M}_{i}} + {{M}_{j}}}}{{{{M}_{i}}{{M}_{j}}}}} \frac{1}{{p\sigma _{{i,j}}^{2}\Omega _{{i,j}}^{{(1,1) * }}}},\,\,{\text{c}}{{{\text{m}}}^{2}}{\text{/s,}}$$

where xi is the relative mole ratio, \({{x}_{i}} = {{{{p}_{i}}} \mathord{\left/ {\vphantom {{{{p}_{i}}} {p = {{Y}_{i}}{{{{M}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{M}_{\Sigma }}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}}}} \right. \kern-0em} {p = {{Y}_{i}}{{{{M}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{M}_{\Sigma }}} {{{M}_{i}}}}} \right. \kern-0em} {{{M}_{i}}}}}}\), σi is the radius of a particle of the ith kind in Å; \(\Omega _{i}^{{(2,2) * }} = f\left( {{{T}_{i}}} \right)\) is the collision integral for the viscosity and the thermal conductivity, and \({{T}_{i}} = {{kT} \mathord{\left/ {\vphantom {{kT} {{{\varepsilon }_{i}}}}} \right. \kern-0em} {{{\varepsilon }_{i}}}}\), where εi is the Lennard–Jones potential parameter that characterizes the potential well depth. The collision integrals for the viscosity and the diffusion were calculated from the Anfimov approximations

$$\Omega _{i}^{{(2,2) * }} = 1.157T_{i}^{{ - 0.1472}},\quad \Omega _{{i,j}}^{{(1,1) * }} = 1.074T_{{i,j}}^{{ - 0.1604}}.$$

In calculations of the functions that determine the viscosity, the thermal conductivity, and the diffusion we also used the combinatorial formulas of the following form:

$${{T}_{{i,j}}} = \frac{{kT}}{{{{\varepsilon }_{{i,j}}}}},\quad {{\varepsilon }_{{i,j}}} = \sqrt {{{\varepsilon }_{i}}{{\varepsilon }_{j}}} ,\quad {{\sigma }_{{i,j}}} = \frac{1}{2}\left( {{{\sigma }_{i}} + {{\sigma }_{j}}} \right).$$

The thermal-radiation transfer equation (1.7) formulated in the general form with respect to the spectral radiation intensity for a nondissipative medium was solved in the multigroup approximation when the total spectral range of the wavenumbers \({{\omega }_{{{\text{tot}}}}} \in [1000,20{\kern 1pt} {\kern 1pt} 000]\) cm–1 is divided into Ng spectral groups, the average absorption coefficient \({{\kappa }_{g}} = \frac{1}{{\Delta {{\omega }_{g}}}}\int_{\Delta {{\omega }_{g}}} {{{\kappa }_{\omega }}d\omega } \) being introduced within each of them.

In the problem under consideration the main radiation processes are the rotational-vibrational bands of the di- and triatomic CO, H2O, and CO2 molecules. To calculate the spectral molecular cross-sections we used both the data [33] and the spectral optical models implemented in the ASTEROID computer system of calculations of the spectral optical properties of high-temperature gases [34]. The local thermodynamic equilibrium approximation was used. The total spectral range was divided into 99 inhomogeneous spectral sections (spectral groups) with the aim to take into account the vibrational structure of the absorption and radiation spectra of the combustion products in the best way. The boundaries of the spectral domain taken into account were chosen with regard to the fact that, in accordance with Wien’s law, the main part of thermal radiation is emitted in the infrared spectrum domain over the temperature range considered. The spectral absorption coefficient was calculated from the formula

$${{\kappa }_{\omega }} = \sum\limits_i^{{{N}_{s}}} {{{\sigma }_{{\omega ,i}}}{{N}_{i}}} ,$$

where \({{\sigma }_{{\omega ,i}}}\) is the spectral absorption cross-section of the ith component and Ni is the number density of particles of the ith kind determined from the formula

$${{N}_{i}} = 0.725 \times {{10}^{{16}}}\frac{p}{T}\frac{{{{M}_{\Sigma }}}}{{{{M}_{i}}}}{{Y}_{i}},\,\,{\text{c}}{{{\text{m}}}^{3}},$$

in which the pressure р is measured in erg/cm3.

Taking specifics of the gasdynamic channel geometry into account, to solve Eq. (1.7) we use the plane-layer model within the framework of which the absorption coefficient and the Planck function depend only on the normal coordinate y, while the spectral radiation intensity depends on the coordinate y and the angle \(\theta \) between the y axis and the direction of radiation. In this approximation, instead of Eq. (1.7), it is convenient to use the following system of first-order differential equations for four semi-flexible (semi-moment) functions [35]

$$\frac{{dM_{{0,g}}^{ + }}}{{d{{\tau }_{g}}}} + 6M_{{0,g}}^{ + } - M_{{1,g}}^{ + } = 6\pi {{J}_{{b,g}}},\quad g = 1,\;2,\; \ldots ,\;{{N}_{g}},$$
(1.9)
$$\frac{{dM_{{1,g}}^{ + }}}{{d{{\tau }_{g}}}} + M_{{0,g}}^{ + } = 2\pi {{J}_{{b,g}}},\quad g = 1,\;2,\; \ldots ,\;{{N}_{g}},$$
(1.10)
$$\frac{{dM_{{0,g}}^{ - }}}{{d{{\tau }_{g}}}} - 6M_{{0,g}}^{ - } - 6M_{{1,g}}^{ - } = - 6\pi {{J}_{{b,g}}},\quad g = 1,\;2,\; \ldots ,\;{{N}_{g}},$$
(1.11)
$$\frac{{dM_{{1,g}}^{ - }}}{{d{{\tau }_{g}}}} + M_{{0,g}}^{ - } = 2\pi {{J}_{{b,g}}},\quad g = 1,\;2,\; \ldots ,\;{{N}_{g}},$$
(1.12)

where \({{\tau }_{g}} = \int_0^y {{{\kappa }_{g}}dy} \) is the optical thickness of the gas layer in the gth spectral group,

$$M_{{n,g}}^{ + } = \int\limits_{\Delta {{\omega }_{g}}}^{} {\left( {2\pi \int\limits_0^1 {J_{\omega }^{ + }{{\mu }^{n}}d\mu } } \right)d\omega ,\quad M_{{n,g}}^{ - } = \int\limits_{\Delta {{\omega }_{g}}}^{} {\left( {2\pi \int\limits_{ - 1}^0 {J_{\omega }^{ - }{{\mu }^{n}}d\mu } } \right)d\omega ,\quad n = 0,1,} } $$
(1.13)

\(J_{{b,g}}^{{}} = \int\limits_{\Delta {{\omega }_{g}}} {J_{{b,\omega }}^{{}}} d\omega \) is the group intensity of the perfectly black body, \(\mu = {\text{cos}}({{\theta }^{ \wedge }}y)\), and \(\Delta {{\omega }_{g}} = {{\omega }_{{g + 1}}} - {{\omega }_{g}}\).

To determine the spectrum-integral radiation flux towards unit area on the surface with the normal n, it is necessary to carry out integration

$${{q}_{R}} = \int\limits_{{\text{4}}\pi } {{\text{d}}\Omega } \int\limits_{\Delta {{\omega }_{{tot}}}} {{{J}_{\omega }}\left( {{\mathbf{r}},\Omega } \right)\left( {{\mathbf{n}} \cdot {\mathbf{\Omega }}} \right){\text{d}}\omega } = \int\limits_{{\text{4}}\pi } {\left( {\sum\limits_{g = 1}^{{{N}_{g}}} {{{J}_{g}}\left( {{\mathbf{r}},\boldsymbol{\Omega} } \right)} \Delta {{\omega }_{g}}} \right)\left( {{\mathbf{n}} \cdot {\mathbf{\Omega }}} \right){\text{d}}\Omega } .$$

Taking into account the definition of semi-moment characteristics (1.13), we obtain the following expression for the density of integral radiation fluxes directed to the upper and lower surfaces:

$${{q}_{R}}(y = 0) = 2\pi \left| {\sum\limits_{n = 1}^{{{N}_{g}}} {M_{{1,n}}^{ - }} } \right|,\quad {{q}_{R}}(y = H) = 2\pi \sum\limits_{n = 1}^{{{N}_{g}}} {M_{{1,n}}^{ + }} .$$

In integrating the system of equations (1.1)–(1.6), there is no need to solve the Ng systems of differential equations (1.9)–(1.12) in each time step, since such an algorithm is not very economic. It is sufficient to make this only for the most characteristic structures of gasdynamic fields. In the case of an appreciable influence of emission and reabsorption of thermal radiation on gas dynamics of the process, such calculations should be made in each time step. Note that within the framework of the semi-moment method the total thermal extraction (heat release) in the volume of hot radiating gas can be determined from the formula [35]

$${{Q}_{{v}}} = \sum\limits_{g = 1}^{{{N}_{g}}} {2\pi {{\kappa }_{g}}} [2{{J}_{{b,g}}} - (M_{{0,g}}^{ + } + M_{{0,g}}^{ - })].$$

The surface of the scramjet combustion chamber was assumed to be catalytic, i.e., it was assumed that equilibrium in the reacting mixture of gases is reached on the internal surfaces. This equilibrium corresponds to the current pressure and a given temperature of the combustion chamber wall Tw. The series of numerical experiments with formulation of the non-catalytic conditions on the boundary, i.e., vanishing the diffusive fluxes

$$\frac{{\partial {{{\left( {{{Y}_{i}}} \right)}}_{w}}}}{{\partial y}} = 0,\quad i = 1,\;2,\;3,\; \ldots ,\;{{N}_{s}}$$

did not lead to the qualitative modification of the solution, although the density of convective heat fluxes turned out to be lower.

At inlet to the channel (at x = 0 in Fig. 1a, flow from left to right) the boundary conditions were imposed in accordance with [8] and given in Table 2. The emissivity factor of the surface was specified to be equal to 0.8.

2 RESULTS OF THE NUMERICAL SIMULATION

Taking the gasdynamic channel geometry (Fig. 1) and the main initial data (the air velocity and the pressure and temperature pinp and Tinp at air-intake inlet) together with the constant Mach number M = 2.2, the chamber surface temperature Tw = 400 K, and the combustible mixture velocity in injection to the combustion chamber Vinj = 60 000 cm/s as the base, the numerical investigation was carried out for various fuel (ethylene-air mixture) flow rate through the atomizers located inside the cavity. Variants of a single or two injection zones (marked by numbers 8 and 9 in Fig. 1 and variants 1–6 and 7, 8 in Table 2, respectively) were considered. In this case the gasdynamic processes were considered at two rising heights of the butterfly valve (5), h = 1 and 2 cm.

In all the variants considered, the density distributions of convective, spectral, and integral radiation heat fluxes were calculated along the lower and upper surfaces of the diffuser (see zone 1 in Fig. 1a), the combustion chamber (zones 2 and 3), and the nozzle (zone 4). The flameholder zone in form of trapezoidal cavity (6) and butterfly valve (5) was especially distinguished. The total force exerted on the surface of the investigated chamber was also calculated in various computational cases in the streamwise direction. The forces calculated and the combustible mixture flow rates were related to 1 cm of the gasdynamic channel width.

The ethylene/air mass ratio in the fuel injected through atomizers was set to be equal to 0.5 (mass fractions of the injected components were as follows: \({{Y}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}}\) = 0.5, \({{Y}_{{{{N}_{2}}}}} = \) 0.5 × 0.78, and \({{Y}_{{{{{\text{O}}}_{{\text{2}}}}}}} = \) 0.5 × 0.22). The optimum relation between the fuel components to ensure the most effective burning was not searched, although in preliminary calculations it was established that the completeness of burning turned out to be appreciably lower at \({{Y}_{{{{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{4}}}}}}}\) = 1.0 in the injected ethylene jets. Both in the first and in the second injection zone the fuel jet was injected either along or counter the x axis (see 8 and 9 in Fig. 1a).

We will consider the results of numerical simulation in the case of a single injection zone at various pressures pinp of the injected jet (see variants 1, 2, and 3 in Table 1).

Table 1. Kinetic ethylene combustion model [21]
Full size table

In the first calculated variant (Fig. 2) we can observe fairly stable ethylene combustion in the cavity domain with periodic ejection of hot gas masses in the direction opposite to main stream along the upper surface of diffusor. Noteworthy is that these ejections (they can be clearly seen in Figs. 2b and 2h) take place with the period of approximately 10 ms and extend over a relatively short time ∼2 ms. In this case the intervals of relatively stable combustion (Figs. 2c–2g) extend over time of the order of  7 ms. Such a pattern replicates with good regularity. In Fig. 3 we have reproduced the typical distributions of basic gasdynamic functions which characterize the quasi-steady combustion process (Figs. 2c–2f). Flow is supersonic over the entire domain of gas dynamic channel in the neighborhood of the lower surface. Flow is subsonic in the cavity. Here, we can observe a clearly expressed periodically pulsing vortex motion. This favors to better mixing of the reacting gas mixture.

Fig. 2.
figure 2

Temperature field (in K) in the combustion chamber at successive instants of time in step \(\Delta t\) = 1.7 ms. Computational variant no. 1. Animated file with the temperature distributions at successive instants of time in step \(\Delta t\) = 0.1 ms is given in application Fig_02App_Var_01_Temp_1InjZ_h1_0.416atm_427K_0.624atm_1800K.avi/

Full size image
Fig. 3.
figure 3

Typical distributions of the Mach numbers (a), the pressure (Pres in atm) (b), and the mass fractions of the combustion products CO (c), CO2 (d), and H2O (e) for the first computational variant.

Full size image

On the lower surface, beneath the cavity, the higher-pressure zone can be observed (Fig. 3b). At the instants of ejections of subsonic stream from the cavity along the upper surface in the direction opposite to main flow, the above-mentioned higher-pressure zone is also displaced upstream to the distance of 35–40 cm from the inlet cross-section.

In Figs. 3c–3e we can clearly see that the intense combustion process with formation of the main combustion products, namely, CO, CO2, and H2O, takes place in the cavity domain. Moreover, these combustion products represent important optically active components, which mainly form thermal radiation towards the internal surfaces of the combustion chamber.

In Fig. 4 we have shown the development of the fuel combustion process during significantly shorter time intervals than those shown in Fig. 2. In Fig. 4 we have reproduced the structure of the temperature field in step \(\Delta t = \) 0.1 ms. We can clearly see that the hot reaction cavity zone generates periodic ejections of heated gas masses along the main stream. The distributions of mass ethylene fractions shown in Fig. 5 demonstrate that masses of unreacted ethylene whose concentration, however, reduces downstream are ejected from the cavity with the same periodicity. In this case the fields of the z-projections of the velocity curl, shown in Fig. 6, confirm relation of these heated gas and unreacted fuel masses with the vortex flow structure. We also note that the time sweep of the vortex field in Fig. 6 demonstrates the vortex structure of gas flow in the cavity.

Fig. 4.
figure 4

Temperature fields (in K) in the combustion chamber at successive instants of time in step \(\Delta t\) = 0.1 ms. Computational variant no. 1.

Full size image
Fig. 5.
figure 5

Fields of the mass ethylene fractions in the combustion chamber at successive instants of time in step \(\Delta t\) = 0.1 ms. Computational variant no. 1. Animated file of unsteady ethylene combustion is given in application. Fig_05App_Var_01_С2Н4_1InjZ_h1_0.416atm_427K_0.624atm_1800K.

Full size image
Fig. 6.
figure 6

Fields of the z-component of velocity curl (in units of 21 513 s–1) in the combustion chamber at successive instants of time in step \(\Delta t\) = 1.7 ms. Computational variant no. 1. Animated file of the field of the z-component of velocity curl at successive instants of time is given in application Fig_06App_Var_01_Vorticity_1InjZ_h1_0.416atm_427K_0.624atm_1800K.avi

Full size image

Based in Figs. 2–4, we can estimate the velocity of motion of hot vortices along the х axis which correlates well with the velocity of the main supersonic flow in the chamber.

Thus, the results of the first computational variant considered above demonstrate implementation of the oscillating dual-mode character of flow. The high-frequency oscillation component at the frequency fh ~ 3000 Hz corresponds to generation of hot gas masses and their drifting downstream, while the low-frequency oscillation component at the frequency fl ~ 200 Hz corresponds to periodic ejection of hot gas masses in the direction opposite to flow from the cavity.

In the variant considered above the completeness of ethylene combustion is not ensured and the effectiveness of this regime is not high. From Fig. 5 we can see that a considerable fraction of fuel is also ejected from the nozzle by periodic vortex structures.

In the second computational variant, in which the pressure in the injected jet was increased by 1.6 times, more regular oscillatory motion of the hot subsonic domain upstream of the cavity can be observed. In this case, while the vortex structures generated in the cavity are drifted downstream at the main flow velocity, a sufficiently stable high-temperature zone with small oscillations along the upper surface can be observed in the neighborhood of the upper surface of the flameholder upstream of the cavity. Within this zone the subsonic motion is implemented and ethylene combustion occurs.

In Fig. 7 we have reproduced the temperature distributions in time step \(\Delta t = \) 0.2 ms. Increase in the pressure in the cavity domain has the significant effect on the distributions of gasdynamic functions along the gasdynamic channel. The zone of subsonic motion increases substantially and occupies approximately half the height of the gasdynamic channel (Fig. 8a) and its leading front reaches the distance x = 28 cm from the inlet cross-section.

Fig. 7.
figure 7

Temperature fields (in K) in the combustion chamber at successive instants of time in step \(\Delta t\) = 0.2 ms. Computational variant no. 2. Animated file with the temperature distributions at successive instants of time in step \(\Delta t\) = 0.2 ms is given in application Fig_07App_Var_02_Temp_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi

Full size image
Fig. 8.
figure 8

Typical distributions of the Mach numbers (a), the pressure (Pres in atm) (b), and the mass fractions of the combustion products C2H4 (c), CO (d), CO2 (e), and H2O (f) for the second computational variant. Animated files with the distributions of the Mach numbers, the z-component of velocity curl, the mass fractions of ethylene and combustion products CO, CO2 , and H2O at successive instants of time in step \(\Delta t\) = 0.2 ms are given in applications, respectively: Fig_08AppA_Var_02_Mach_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi, Fig_08AppB_Var_02_Vorticity_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi, Fig_08AppC_Var_02_C2H4_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi, Fig_08AppD_Var_02_CO_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi, Fig_08AppE_Var_02_CO2_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi, Fig_08AppF_Var_02_H2O_1InjZ_h1_0.416atm_427K_1.0atm_1800K.avi.

Full size image

The relatively high pressure is established in a considerable volume of the combustion chamber (Fig. 8b). As a consequence, we can note the high completeness of ethylene combustion (Fig. 8c). The distributions of main combustion products testify to the fairly high effectiveness of combustions.

Increase in the pressure to 2.5 atm leads to the catastrophic consequences for the process of combustion in the chamber, namely, the shock wave generated in the neighborhood of the cavity goes out continuously in the direction opposite to the air stream to the diffusor.

In the fourth computational variant, a relatively low pressure of the injected fuel was given and the effective ignition temperature was decreased to Tinj = 1200 K. Combustion did not cease but its intensity decreased significantly. Ejection of hot gas from the cavity in the direction opposite to the main stream was not observed, although the periodic outgoing of vortex masses of hot gas was observed, as before. In Fig. 9 we have reproduced the typical distribution of the gasdynamic functions. The zone of subsonic motion is localized in the cavity (Fig. 9b), while the higher pressure, as before, is localized beneath the cavity (Fig. 9c). The distributions of the mass fractions of ethylene and combustion products (Figs. 9d–9g) show the low burning effectiveness.

Fig. 9.
figure 9

Typical distributions of the temperature (a), the Mach numbers (b), the pressure (Pres in atm) (c), and the mass fractions of the combustion products C2H4 (d), CO (e), CO2 (f), and H2O (g) for the fourth computational variant.

Full size image

In Fig. 10 we have reproduced the results of the numerical simulation of combustion under the higher-pressure conditions at the chamber inlet (variant 5 in Table 2). In this case generation of the backpressure in cavity is insufficient for propagation of the hot subsonic flow region upstream; therefore, the basic ethylene combustion zone is localized in the neighborhood of the cavity (Fig. 10a). As before, the hot ethylene masses, which thereafter are drifted downstream, are periodically carried out from the combustion zone. As judged by Figs. 10d–10g, ethylene combustion occurs more effectively. The intense vortex motion at the subsonic velocity can be observed in the cavity domain (Fig. 10b), while the higher-pressure domain which is almost at rest is localized in the neighborhood of the lower surface (Fig. 10c).

Fig. 10.
figure 10

Typical distributions of the temperature (a), the Mach numbers (b), the pressure (Pres in atm) (c), and the mass fractions of the combustion products C2H4 (d), CO (e), CO2 (f), and H2O (g) for the fifth computational variant.

Full size image
Table 2. Input data and results of calculation of the total forces exerted on the internal surface of the combustion chamber in the streamwise direction
Full size table

In the final variant no. 6 of the calculation series for a single fuel injection zone the height of rising the butterfly valve 5 (Fig. 1a) was increased. The other input data remained the same as those in variant 1. The structure of the flow field turned out to be mainly similar to that obtained in the first variant, namely, periodic ejections of the subsonic combustion domain along the upper surface to the distance х ∼ 32 cm are observed, while the burning-gas vortices are drifted at the higher frequency downstream of the cavity. However, an important difference between this and the first variants (the latter has the practical value) is increase in the force \({{F}_{{x,{\text{bot}}}}}\), exerted in the positive direction of the x axis just owing to the risen valve. This means that there is an increase in the total drag of the gasdynamic channel.

In two final variants (nos. 7 and 8) of the calculation series, we have studied the influence of an additional ethylene injection to the cavity (see injection 9 in Fig. 1a) on the combustion process. In the case of variant 7 the additional injection to the cavity was carried out under the conditions similar to the first variant; therefore, an increase in the pressure in cavity should be expected. Just this was observed in our calculations. The results obtained are very similar to variant 2 in which the pressure in the injected fuel jet was of the order of 1 atm. Not only the distributions of the gasdynamic functions and the mass fractions of combustion products in time and space, but also the parameters of the total force impact (compare rows 2 and 7 in Table 1) turned out to be similar.

The use of an additional fuel injection at the height of rising the butterfly valve h = 2 cm (variant 8 in Table 2) showed the results similar to those in variant 6, the projections of the total force on the x axis increasing by approximately 10%.

Thus, the calculated data showed that generation of the additional pressure in the frameholder is practically equivalent to using the butterfly valve. However, in addition to variations in the flow field structure, it is necessary to take into account the force and thermal action of burning gas mixture to the combustion chamber walls. As an example of analysis of these actions, in Figs. 11 and 12 we have reproduced the pressure and density distributions of convective heat fluxes along the upper and lower surfaces for two heights of rising the butterfly valve. The lower surface is subject to the strongest force action. As the height of rising the butterfly valve increases by 1 cm, the region of the strongest force action is displaced in the direction opposite to the stream by approximately 10 cm.

Fig. 11.
figure 11

Pressure distributions in the case of two injection zones on the lower (curves 1 and 2) and upper (curves 3 and 4) surfaces for the heights of the butterfly valve h = 1 cm (curves 1 and 3) and h = 2 cm (curves 2 and 4).

Full size image
Fig. 12.
figure 12

Distributions of the density of convective heat flux in the case of two injection zones on the lower (curves 1 and 2) and upper (curves 3 and 4) surfaces for the heights of the butterfly valve h = 1 cm (curves 1 and 3) and h = 2 cm (curves 2 and 4).

Full size image

The upper surface of combustion chamber in whose neighborhood the high-temperature ethylene combustion products are localized is subject to the strongest thermal action. The density of convective heat fluxes increases in the case of the greater height of rising the butterfly valve.

As noted above, the character of time-dependent self-oscillatory flow in the combustion chamber can be seen in all the calculated cases considered. The heat flux density and the surface pressure vary in time in accordance with the specific unsteady process. Therefore, in Figs. 11 and 12 we have reproduced certain instantaneous by typical structures.

It is obvious that this also relates to the densities of radiative heat fluxes on the internal combustion chamber surfaces. In Fig. 13 we have reproduced the density distributions of convective and radiative heat fluxes over the upper surface in the second variant. As a rule, the highest density of convective heat fluxes is reached in the neighborhood of the cavity. In Fig. 13 we have reproduced the case of the strongest heating of the upper surface downstream and upstream of the cavity. This case corresponds to the flow field structure shown in Fig. 7d. In the cases considered the density of integral radiative heat fluxes amounts to approximately 10% of the convective heat flux level. However, it should be kept in mind that the density of radiative heat fluxes will appreciably increase with the radiating volume.

Fig. 13.
figure 13

Distributions of the densities of convective (solid curve) and integral radiative (broken curve) heat fluxes along the upper surface of the combustion chamber for the second computational variant.

Full size image

SUMMARY

The thermogasdynamic processes that accompany ethylene combustion in the supersonic air flow in a model dual-mode scramjet chamber in which combustion can take place in both sub- and supersonic regimes are studied with the use of the computer radiative-gasdynamic model based in the time-dependent Navier–Stokes, energy conservation, and diffusion equations together with the system of chemical kinetics and selective thermal radiation transfer equations in the multigroup formulation. The process of ethylene combustion is considered within the framework of the three-stage kinetic combustion model so that in calculations 7 components, namely, H2, O2, N2, CO, CO2, H2O, and C2H4, are taken in to account.

The features of flow and combustion in the chamber with the flameholder of a trapezoidal shape located on one of the surfaces are considered under typical conditions at inlet in the gasdynamic channel: М = 2.2, the pressure of 0.416–1 atm, and the temperature of 427–700 К. Variants with one or two zones of injection of an ethylene-air mixture and two configurations of the butterfly valve located at inlet to the nozzle part of the chamber on the lower surface are considered.

It is shown that a periodic self-oscillating combustion regime is formed in the combustion chamber. Two frequency modes of gas flow oscillations are distinguished in this regime. The first high-frequency mode is related to periodic ejection of burning vortex structures from the cavity into which a combustible mixture is injected. The second low-frequency mode is related with periodic ejection of the combustible mixture counter the main gas stream along the upper surface from the cavity. In all the cases considered a vortex oscillating subsonic motion is observed in the cavity.

It is shown that the effects similar to the use of various heights of rising the butterfly valve can be reached using variations in pressure in the flameholder.

The determination of levels of the densities of convective and radiative heat fluxes on the combustion chamber walls that are equal to 10–20 and ~1 W/cm2, respectively, became the result of the thermogasdynamic calculations.