The interest in the process of the total enthalpy \({{i}_{0}}\) redistribution in compressible gas flows, in addition to fundamental interest, relates to the devices able to separate a gas stream into cold and hot streams (with low and high stagnation temperatures) without mechanical work or external heat supply (for example, the Ranque–Hilsch vortex tube or the Leont’ev tube) [1, 2]. At present, various methods for increasing the effectiveness of such devices are being investigated [3–5]. In this connection, the study of the energy separation process (total enthalpy redistribution) in canonical flows is topical. One of the examples of such flows is considered in the present study, namely, energy separation in gas flows past bodies is studied.

The question of energy separation in flows around bodies was discussed in many experimental and theoretical works [6–16]. The basic motivation for these investigations is the Eckert–Weiss effect (or the “aerodynamic cooling effect” [8]) which consists in the formation of a region with the low recovery temperature on the leeward side of the thermally insulated cylinder: under certain conditions the recovery temperature can be lower than the free-stream static temperature.

From the energy conservation law written in dimensionless form (see Section 1)

$$\frac{{d{{i}_{0}}}}{{dt}} = \frac{1}{\rho }\frac{{\partial p}}{{\partial t}} + \frac{1}{{\rho {\text{Re}}}}\nabla \cdot \left( {{\boldsymbol{\tau }} \cdot {\mathbf{u}}} \right) + \frac{\gamma }{{\rho {\text{RePr}}}}{{\nabla }^{2}}T$$
(0.1)

it follows that redistribution of the total enthalpy i0 in fluid particles can occur as a result of pressure fluctuations, work of viscous stresses, and heat conduction. If the unsteadiness and the dissipation mechanisms can be neglected (for example, outside the wake region), then the total enthalpy is conserved in fluid particles. The dissipation mechanisms can be neglected in the developed wake region; therefore, the energy separation process is determined by pressure fluctuations. Generally speaking, all the mechanisms should be taken into account in the neighborhood of the body surface. An estimate of the extent of influence of these mechanisms (terms in Eq. (0.1)) on the basis of numerical calculations [14] confirms these considerations.

The most expressed reduction in i0 is observed in the neighborhood of the rear part of the body. The drop in the total enthalpy along the boundary layer in the front part of the cylinder turns out to be significantly smaller and, consequently, cannot explain this effect. Based on the experimental results [8], a connection between the Eckert–Weiss effect and the vortex formation process was proposed which was also implicitly confirmed in successive experimental studies [7, 9]. In [9] it was shown that the effect attenuates when a separation plate is introduced into the vortex formation region. In [7] considerable decrease in i0 due to intensification of vortices in the resonance between steady acoustic wave frequencies in the aerodynamic tunnel and shedding of vortices was observed. In numerical calculations [16] the impact on the vortex formation process was implemented by varying the distance between two cylinders located across the flow. It was shown that there is a considerable influence of the vortex formation process on the intensity of the Eckert–Weiss effect and an explanation was proposed. In accordance with [16], the effect is determined by the balance of two factors:

(i) cooling—the vortex is formed in the neighborhood of the body surface such that in the initial stage of intensive growth it is displaced to the wake centerline. In this case the pressure in the vortex decreases, i.e., the first term in Eq. (0.1) is negative. This is the basic reason for the formation of cooled fluid regions in the neighborhood of the rear part of body.

(ii) heating—in the following stage, when the appearing vortex is being displaced downstream and shedded into the stream, intense gas flow develops in the gap between the rear part of the cylinder and the vortex. This stream fills the space in the neighborhood of the body with heated gas that appears as a result of pressure fluctuations in the shear layers shedding from the body. Moreover, since the vortex core represents the reduced pressure region, we have \(\partial p{\text{/}}\partial t > 0\) behind the vortex that travels downstream. These facts have the opposite effect by tending to increase the time-averaged stagnation enthalpy.

Thus, even though all three mechanisms are commensurable in the neighborhood of the rear part of the body surface, cooling of the body surface is determined by the non-dissipative term. Modification in the regime of interaction of the shedding vortices with the body surface can lead to a considerable increase in the intensity of these processes. In Subsection 2.1 we will discuss the influence of the body shape on the Eckert–Weiss effect and the distribution of \({{i}_{0}}\) in the vortex formation region.

A representation of the total enthalpy distribution in the developed wake can be obtained based on the experimental data and the results of numerical simulation [7, 9, 12, 14–16]. Time-averaged total enthalpy \(\overline {{{i}_{0}}} \) takes reduced values in the neighborhood of the wake centerline (here and in what follows, the time-averaged quantities are denoted by a bar on top). The minima are reached in the vortex formation region. The effect attenuates with the distance downstream. However, it should be noted that tending \(\overline {{{i}_{0}}} \) to the free-stream value \({{i}_{{0\infty }}}\) can be non-monotonic due to the restructuring of the developed vortex wake that leads to the appearance of local extrema of  \(\overline {{{i}_{0}}} \).

As noted above, the energy separation process in the developed wake can be described by neglecting the impact of viscous forces and heat conduction. In [7] gas cooling in the neighborhood of the wake centerline was explained as follows. In the developed wake the fluid particle trajectories are structured in such a way that ahead of (behind) the vortices the particles travel to (from) the wake region. Taking into account the fact that the vortex core pressure is reduced, we have \(\partial p{\text{/}}\partial t < 0\) (\(\partial p{\text{/}}\partial t > 0\)) ahead of (behind) the vortex. Therefore, in accordance with Eq. (0.1) \({{i}_{0}}\) decreases when particles move towards the central part of the wake. In [14] variation in the total enthalpy along trajectories was given on the basis of numerical calculations.

Using the von Karman street model based on infinite vortex chains, the following relation between the total enthalpy and the parameter of the vortex street along the wake centerline can be established [7, 15]:

$$\overline {{{i}_{0}}} - {{i}_{{0\infty }}} = - \frac{{{{\Gamma }_{0}}}}{l}(1 + U).$$
(0.2)

Here, \(l\) is the von Karman street period, \({{\Gamma }_{0}}\) and \(1 + U\) are the circulation of vortices and their velocity in the coordinate system moving with the cylinder. In [15] this idea was applied to the case of wakes consisting of \(N\) vortex chains and the agreement between the estimates obtained on the basis of this simplified model and the numerical results was demonstrated. One of the main difficulties in constructing these models is the assumption on the temperature distribution in the vortex cores, which can be affected by the vortex formation process. This question will be discussed in Subsections 2.2 and 2.3 based on the numerical experiment.

The applicability of such estimates is complicated in the situation with irregular large-scale vortex structures in the wake. However, in calculations and experiments (see [16]) a similarity of the time-averaged velocity and total enthalpy profiles is observed, the following inequality being usually fulfilled

$$\mathop {\max}\limits_y [{{i}_{{0\infty }}} - \overline {{{i}_{0}}} (x,y)] < \mathop {\max}\limits_y [1 - \bar {u}(x,y)].$$

This inequality agrees with Eq. (0.2) and can be obtained independently for the asymptotic far wake when Pr < 1.

In the present study the processes of the total enthalpy redistribution in the near wake behind an elliptic cylinder and a pair of cylinders are considered on the basis of numerical simulation. The initial and boundary-value problems are solved for the Navier–Stokes equations that describe two-dimensional viscous perfect gas flows at the Reynolds number \({\text{Re}} = 1000\), the Mach number \({{{\text{M}}}_{\infty }} = 0.4\), and the Prandtl number \({\text{Pr}} = 0.72\). The formulation of the problem of a flow around bodies and the numerical method are described in Section 1. The simulation results are discussed in Section 2. Most attention is given to the questions of the influence of the body shape on the intensity of energy separation (Subsection 2.1), the onset of regions with reduced total enthalpy \({{i}_{0}}\) in the developed wake and adequacy of the results of a simplified model for describing these regions (Subsections 2.2 and 2.3).

1 FORMULATION OF THE PROBLEM AND NUMERICAL METHOD

1.1 Formulation of the Problem

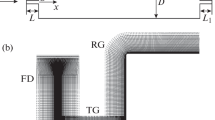
We will consider the problems of flow past an elliptic-cross-section cylinder and the pair of side-by-side circular cylinders in the Cartesian coordinate system \((x',y')\) taken as follows: the free-stream velocity is equal to \(({{u}_{\infty }},0)\), in the case of the elliptic cylinder its center is at the origin, while in the case of the pair of side-by-side cylinders their centers are located at points \((0,0)\) and \((0,L)\). It is convenient to parametrize the elliptic cylinder cross-section using the length of the major axis of the ellipse D and the compression parameter \(k\) which is equal to the ratio of the lengths of semiaxes along the \(y'\) and \(x'\) coordinate axes (see Fig. 1). Thus, at \(k = 1\) the problem corresponds to a flow past a circular cylinder of diameter D, at \(k = 0\) and \(k = \infty \) the problem corresponds to a flow past an infinitely thin plate of depth D located along and across the flow, respectively. In the case of the pair of circular cylinders there are also two parameters which determine the flow geometry, namely, the diameter of cylinders D and the distance between their centers \(L\).

Fig. 1.
figure 1

Diagram of flow past an elliptic cylinder.

Full size image

Fluid flow can be described by the model of a viscous perfect gas with constant specific heats \({{c}_{V}}\) and \({{c}_{p}}\) at constant volume and pressure, respectively, and the heat conductivity and viscosity coefficients \(\kappa \) and \(\mu \). The Navier–Stokes equations will be solved; in dimensionless form they take the form:

$$\begin{gathered} \frac{{d\rho }}{{dt}} + \rho \nabla \cdot {\mathbf{u}} = 0, \\ \rho \frac{{d{\mathbf{u}}}}{{dt}} = - \nabla p + \frac{1}{{{\text{Re}}}}\nabla \cdot {\boldsymbol{\tau }}, \\ \rho \frac{d}{{dt}}\left( {T + \frac{1}{2}{{{\mathbf{u}}}^{2}}} \right) = - \nabla \cdot (p{\mathbf{u}}) + \frac{1}{{{\text{Re}}}}\nabla \cdot \left( {{\boldsymbol{\tau }} \cdot {\mathbf{u}}} \right) + \frac{\gamma }{{{\text{RePr}}}}{{\nabla }^{2}}T, \\ p = (\gamma - 1)\rho T. \\ \end{gathered} $$

Here, \(\tau \) is the viscous stress tensor with the following components:

$$({{\tau }_{{ij}}}) = \left( {\begin{array}{*{20}{c}} {\frac{4}{3}\frac{{\partial u}}{{\partial x}} - \frac{2}{3}\frac{{\partial {v}}}{{\partial y}}}&{\frac{{\partial u}}{{\partial y}} + \frac{{\partial {v}}}{{\partial x}}} \\ {\frac{{\partial u}}{{\partial y}} + \frac{{\partial {v}}}{{\partial x}}}&{\frac{4}{3}\frac{{\partial {v}}}{{\partial y}} - \frac{2}{3}\frac{{\partial u}}{{\partial x}}} \end{array}} \right),$$

\(\rho (x,y,t),p(x,y,t),{\mathbf{u}}(x,y,t) = (u,{v})\), and \(T(x,y,t)\) are the density, the pressure, the velocity vector, and the temperature, respectively, and \(\gamma = 1.4\) is the specific heat ratio. The Reynolds, Prandtl, and Mach numbers are introduced as follows:

$${\text{Re}} = \frac{{{{\rho }_{\infty }}{{u}_{\infty }}D}}{\mu },\quad {\text{Pr}} = \frac{{\mu {{c}_{p}}}}{\kappa },\quad {{{\text{M}}}_{\infty }} = \frac{{{{u}_{\infty }}}}{{{{c}_{\infty }}}},$$

where \({{\rho }_{\infty }}\) is the free-stream density and \({{c}_{\infty }} = \sqrt {\gamma {{p}_{\infty }}{\text{/}}{{\rho }_{\infty }}} \) is the speed of sound in the free stream. Nondimensionalization is carried out using the following relations:

$$t = \frac{{{{u}_{\infty }}t'}}{D},\quad {\mathbf{x}} = \frac{{{\mathbf{x}}'}}{D},\quad p = \frac{{p'}}{{{{\rho }_{\infty }}u_{\infty }^{2}}},\quad {\mathbf{u}} = \frac{{{\mathbf{u}}'}}{{{{u}_{\infty }}}},\quad T = \frac{{{{c}_{V}}T'}}{{u_{\infty }^{2}}}.$$

Here, the dimensional quantities are denoted by primes.

The equations are solved in variables \((p,{\mathbf{u}},T)\) for which the following boundary conditions are imposed:

– on the cylinder surface \({\mathbf{u}} = (0,0)\) and \(\nabla T \cdot {\mathbf{n}} = 0\) (here, n is the unit vector of the outward normal);

– at infinity \({\mathbf{u}} = (1,\;0)\), \(p = 1{\text{/}}(\gamma {\text{M}}_{\infty }^{2})\), and \(T = {1 \mathord{\left/ {\vphantom {1 {[\gamma (\gamma - 1){\text{M}}_{\infty }^{2}]}}} \right. \kern-0em} {[\gamma (\gamma - 1){\text{M}}_{\infty }^{2}]}}\).

The initial conditions are specified by introducing a finite time interval in which the cylinder (cylinders) is (are) smoothly accelerated from rest (with the corresponding change in the boundary conditions and supplementing the inertia forces to the equations).

The solution of equations depends on the following parameters: the Reynolds, Prandtl, and Mach numbers \({\text{Re}}\), Pr, and \({{{\text{M}}}_{\infty }}\) and the compression parameter \(k\) (the case of elliptic cylinder) or the distance between the cylinders \(L{\text{/}}D\) (the case of a pair of side-by-side cylinders).

We should mention the constraints of the model connected with neglecting some aspects of real physics of flow such as three-dimensionality and fine-scale turbulent fluctuations. The absence of these aspects in the model is not an obstacle for correct description of the key physical reasons for redistribution of the total enthalpy since the model includes: all three possible mechanisms of change in the total enthalpy in a fluid particle (see Eq. (0.1)); the distinctive features of flow which affect the total enthalpy redistribution (the process of vortex formation, vortex streets, and the effect of compressibility). In [16] the correspondence between the results of calculations within the framework of the used model and the experimental data is discussed in detail.

1.2 Numerical Method

In this subsection we will briefly describe the used numerical method, more detailed information can be found in [14, 16].

The problems are solved numerically by means of the stabilized finite-element method (the Galerkin least-squares method) on unstructured triangular meshes. The implicit Euler scheme is used for calculations in time. The system of nonlinear algebraic equations obtained by discretization is solved by means of the iteration Newton method in combination with the generalized minimum residual method. To diminish the effect of the artificial far boundaries the solution is constructed in the large computational domain: \([ - 200,\;400] \times [ - 200,\;200]\).

The computational mesh has the nested structure with the following resolution in the domains which are of interest to us: the step is equal to approximately 0.025 and 0.0005 in the near wake (\( - 1.5 \leqslant x \leqslant 26\)) and in the neighborhood of the cylinder surfaces, respectively. This corresponds to approximately 40–70 computational nodes across the formed vortices and the dynamic and thermal boundary layers at \({\text{Re}} = {{10}^{3}}\) and \({\text{Pr}} = 0.72\). The time step is \(\Delta t = 0.0025\).

For the considered flow regimes the detailed investigation of how the numerical method parameters (time step and mesh resolution) influence the solution (integral characteristics, frequencies, total enthalpy distribution in the wake) as well as the comparison with the data of other authors are given in [14, 16]. It is shown that the decrease in the taken mesh resolution and the time step does not lead to a significant change in the results.

2 RESULTS

2.1 Influence of the Body Shape on the Reduced Total Enthalpy Regions

In Fig. 2 we have given an example of the influence of the body shape on the distribution of \(\overline {{{i}_{0}}} \) at \({\text{Re}} = 1000\), \({{{\text{M}}}_{\infty }} = 0.4\), and \({\text{Pr}} = 0.72\). For the problem of flow around an elliptic cylinder the parameter \(k\) was taken from the interval \(0.1 \leqslant k \leqslant 10\) on which the wake varies from a narrow steady-state wake without vortex formation at \(k = 0.1\) to a wide wake with the formation of large high-intensity vortices at \(k = 10\). The case of flow past a pair of circular side-by-side cylinders at \(L{\text{/}}D = 1.1\), in which the wake behind the pair of cylinders becomes similar to the flow behind a single body with common vortex street, is also considered. In Fig. 2 the characteristic length for this problem was taken to be equal to \(2.1D\) (in the middle cross-section) for the comparison with the flow past the elliptic cylinder. The geometry of the pair of bodies is close to the case \(k = 2\). This is manifested in similar flow patterns and intensity of redistribution of the total enthalpy (however, the vortex wake behind the pair of cylinders turns out to be less ordered).

Fig. 2.
figure 2

Redistribution of the total enthalpy in flow past bodies of various shapes: figures (a, b) correspond to the instantaneous and time-averaged total enthalpy distributions, respectively; figures (c, d) correspond to the contribution of the internal and kinetic energies to the distribution of \(\overline {{{i}_{0}}} \): \(\overline {{{i}_{0}}} {\text{/}}{{i}_{{0\infty }}} - 1\) = \(\gamma (\overline T - {{T}_{\infty }}){\text{/}}{{i}_{{0\infty }}} + (\overline {{{u}^{2}}} + \overline {{{{v}}^{2}}} - 1){\text{/}}(2{{i}_{{0\infty }}})\). In the case of \(k = 0.1\) in figures (a, b) the color scale is diminished by 10 times. Vorticity isolines (except for the steady-state case at \(k = 0.1\)) are plotted at the instant of time that corresponds to the local maximum of the lift coefficient (red and blue colors of the curves correspond to \(\omega = 1\) and \( - 1\), respectively).

Full size image

In Fig. 2a we have reproduced the flow patterns at the instant of time that corresponds to the local maximum of the lift coefficient. Gas volumes with the higher (reduced) total enthalpy are transported together with vortices so that in the part of vortex which is internal (external) with respect to the wake centerline we have \({{i}_{0}} < {{i}_{{0\infty }}}\) (\({{i}_{0}} > {{i}_{{0\infty }}}\)). Therefore, in time-averaging (Fig. 2b) we have a reduction in \(\overline {{{i}_{0}}} \) in the central part of the wake. Such an inhomogeneity of \({{i}_{0}} = \gamma T + ({{u}^{2}} + {{{v}}^{2}}){\text{/}}2\) in the vortices is attributable to the kinetic energy distribution in the coordinate system connected with the cylinder, in the internal (external) part the kinetic energy is smaller (greater) than its value in the free stream.

From Figs. 2c and 2d we can see that the contribution of the internal and kinetic energies to redistribution of \(\overline {{{i}_{0}}} \) is ambiguous and depends significantly on k. When \(k = 0.5\) and \(1\) the kinetic energy redistribution is favorable to the increase in \(\overline {{{i}_{0}}} \) in the developed wake and the decrease in \(\overline {{{i}_{0}}} \) in the vortex formation region. When \(k \geqslant 2\) we have the opposite case: the mean velocity and the kinetic energy decrease in the central part of the wake due to the increase in the transverse distance between the vortices and their circulation, while in the vortex formation region the kinetic energy increases due to intense cross flow in vortex formation. In steady-state flow (\(k = 0.1\)) \({{i}_{0}}\) reduces in the central part due to negative contribution of the kinetic energy. In the near wake the time-averaged temperature also significantly depends on the wake structure and the process of vortex formation: at small \(k\) the time-averaged temperature in the wake is higher than the static temperature and, therefore, it tends to increase \({{i}_{0}}\); on the contrary, at the large \(k\) the temperature becomes considerably lower than \({{T}_{\infty }}\) and is favorable to increase the energy separation intensity. The cause of such a behavior is the balance between vortex heating and cooling in the process of vortex formation discussed in Subsection 2.3.

The intensity of redistribution of the total enthalpy (energy separation intensity) in the domain \(\Omega \) can be estimated from the local minimum of the time-averaged normalized total enthalpy:

$$E = \left| {\mathop {\min}\limits_{(x,y) \in \Omega } \frac{{\overline {{{i}_{0}}} (x,y) - {{i}_{{0\infty }}}}}{{{{i}_{{0\infty }}}}}} \right|.$$

The values of \(E\) are calculated on the cylinder surface and for two regions \(\Omega \) in the near wake, namely, the vortex formation region and the developed-wake region, in which the local minima of \(\overline {{{i}_{0}}} \) can be clearly observed (except the cases \(k = 0.1\) and 0.5, see Fig. 2b). When \(k \geqslant 0.5\) the total enthalpy reaches minima in the vortex formation region (Fig. 3). In this region the quantity \(E\) increases with \(k\) and reaches \(6.9\% \) at \(k = 10\). As can be seen from Fig. 2, this is connected with the decrease in the mean temperature. Energy separation is most intense in the developed wake also at \(k = 10\), E reaches 4.7%. This differs only slightly from the value of \(E\) at \(k = 2\) (4.5%); however, in this case the area of the region with reduced values of \(\overline {{{i}_{0}}} \) is appreciably greater. The increase in the area is connected with the growth of the transverse distance between the vortices.

Fig. 3.
figure 3

Energy separation efficiency \({{\min}_{{(x,y)}}}(\overline {{{i}_{0}}} {\text{/}}{{i}_{{0\infty }}} - 1)\) calculated on the cylinder surface, in the vortex formation region, and in the developed wake (the region in which the minimum was sought was bounded: x < 11). Light-grey strikes indicate that in flow past an elliptic cylinder with small \(k\) there is no local minimum in the region considered.

Full size image

In Fig. 4 we have plotted the distribution of the recovery coefficient \(r = 2({{i}_{0}} - {{i}_{{0\infty }}}) + 1\) over the cylinder surface. We can see that the recovery coefficient drops sharply in the rear part of the body as soon as steady-state flow in the near wake becomes unstable and vortices (\(k > 0.1\)) begin to be formed. This confirms the connection of the process of vortex formation with the Eckert–Weiss effect. In the highest degree this effect is manifested at \(k = 10\), namely, a wide region with negative recovery coefficient develops, at the point θ = 180° the temperature being lower than the free-stream static temperature by 0.6%. It should be noted that the dependence \({{\min}_{\theta }}r(\theta )\) on \(k\) is non-monotonic; to explain this fact and the presence of local extrema in the dependence \(r(\theta )\), it is necessary to consider in detail, similarly to [16], the process of vortex formation and the balance between the processes of heating and cooling in the rear part of body described in the introduction.

Fig. 4.
figure 4

Distribution of the recovery coefficient r over the surface of an elliptic cylinder.

Full size image

2.2 Model of Total Enthalpy Redistribution in the Developed Wake

We will consider the simplified wake model which makes it possible to explain qualitatively the redistribution of \({{i}_{0}}\). Similar models for vortex streets and individual vortices were discussed, in particular, in [7, 9, 10, 15]. We will assume that in the developed wake

(1) the dissipation processes (the second and third terms in Eq. (0.1)) can be neglected, then variation in the enthalpy is described by the equation

$$\frac{{d{{i}_{0}}}}{{dt}} = \frac{1}{\rho }\frac{{\partial p}}{{\partial t}};$$
(2.1)

(2) flow in the coordinate system moving with the vortices traveling along the x axis can be considered to be steady-state, then from relation (2.1) it follows that in this coordinate system the total enthalpy \(i_{0}^{ * }\) is constant along the streamlines:

$$i_{0}^{ * } = \gamma T + \frac{1}{2}[\mathop {\left( {u - 1 - U} \right)}\nolimits^2 + {{{v}}^{2}}] = C = {\text{const,}}$$
(2.2)

where 1 + U is the velocity of the centers of vortices;

(3) constant C is the same (\(C = \gamma {{T}_{\infty }} + 0.5{{U}^{2}}\)) inside and outside of vortex cores. This makes it possible to write the following explicit expression for the temperature as a function of the velocity:

$$\gamma (T - {{T}_{\infty }}) = (1 + U)(u - 1) - \frac{1}{2}({{u}^{2}} + {{{v}}^{2}} - 1).$$
(2.3)

The total enthalpy (or temperature) distribution inside the core is one of the main difficulties in constructing such models since there are mechanisms which are able to both increase and reduce the temperature (and total enthalpy) the vortices during their formation; as the vortices travel downstream, the temperature distribution in the cores can change qualitatively (for example, in [16] a situation was given when in the near wake the vortices are cooled, \(T < {{T}_{\infty }}\), and in the far wake the vortices are heated, \(T > {{T}_{\infty }}\)).

A straightforward way to close the model used in the present study is the assumption that in the vortex also, as mentioned above, \(C = \gamma {{T}_{\infty }} + 0.5{{U}^{2}}\). Thus, relation (2.3) is assumed to be fulfilled over the entire domain of the developed wake. In [7] the model in which the static temperature in the vortex core was assumed to be constant (the velocity field was described by the pair of vortex chains consisting of the Rankine vortices). The use of this model for the velocity field obtained numerically is complicated by the necessity to determine the core boundaries under an additional restriction related to the continuity of temperature, i.e., in accordance with (2.2), the relation \(\mathop {\left( {u - 1 - U} \right)}\nolimits^2 + {{{v}}^{2}} = {\text{const}}\) must be fulfilled on the core boundary. The method for constructing such a boundary correctly is not evident. Therefore, this model can be more conveniently used together with a certain velocity field approximation (for example, using the Rankine vortices). In Subsection 2.3 we will discuss to what extent both these assumptions on the temperature distribution in vortices agree with numerical calculations.

In literature there is also a model with the isentropic temperature distribution over the vortex \(T = {{T}_{\infty }}\mathop {(p{\text{/}}{{p}_{\infty }})}\nolimits^{1 - 1/\gamma } \) [17]. In this case, in addition to the velocity field, it is necessary to know the pressure or density distribution in the developed wake. Since in the cases considered the entropy in vortices turns out to be significantly higher than the free-stream entropy, the model gives strongly reduced values of the temperature in vortices (when the pressure obtained from the numerical calculation is used) and is not considered in the present study.

Using (2.3), we obtain the following expression for the total enthalpy:

$${{i}_{0}} - {{i}_{{0\infty }}} = \gamma (T - {{T}_{\infty }}) + \frac{1}{2}({{u}^{2}} + {{{v}}^{2}} - 1) = (1 + U)(u - 1).$$
(2.4)

To reach the minimum values of \(\overline {{{i}_{0}}} - {{i}_{{0\infty }}}\), it is advantageous to have the large velocity defect \(1 - \bar {u}\) (usually, \(1 - \bar {u} > 0\)), but, simultaneously, to have also the high vortex velocity 1 + U (usually,\( - 1 < U < 0\)). As can be seen from Eq. (2.3), the latter fact is directly connected with the temperature distribution, namely, within the framework of this model, the increase in the vortex velocity 1 + U at a fixed velocity defect (\(1 - \bar {u}\)) decreases the mean temperature.

From Figs. 5a and 5b it can be seen that the model reproduces the distribution of \({{i}_{0}}\) qualitatively. Here, the velocity 1 + U was determined on based on the vortex distinguished by heavy curve as the velocity at the point of local maximum vorticity. Comparison is meaningful only in the neighborhood of this vortex.

Fig. 5.
figure 5

Comparison of the total enthalpy (a and b) and the temperature (c, d) obtained by solving the Navier–Stokes equations (a, c) and predicted from the velocity field (b, d): formulas (2.3) and (2.4). In the figure the vorticity isolines are also plotted (red and blue colors correspond to \(\omega = 1\) and \( - 1\), respectively); heavy dashed curve denotes the vortex from which the velocity \(U\) was determined. The instant of time corresponds to the local minimum of the lift coefficient.

Full size image

To use the model, it is sufficient to know the velocity field in the developed vortex wake. Using the point-vortex model (or a generalization, for example, by replacing the point vortices with the Rankine vortices), the problem of finding the wake configurations, which are optimum from the point of view of the energy separation intensity, can be solved by relating the velocities \(u\) и U to the characteristics of an idealized vortex wake (the number of vortex chains, the distance between the vortices, the circulation of vortices, see, for example, relation (0.2)) [7, 15].

2.3 Comparison of the Results of Numerical Experiment and the Model

In essence, the model described above gives the explicit expression for the temperature (2.3). From Figs. 2c and 2d it can be seen that the contributions to \(\overline {{{i}_{0}}} \) from redistribution of the internal and kinetic energies are commensurable in the regimes considered. Consequently, the choice of the model for the temperature distribution in vortices is significant when describing energy separation in the wake. In this section we will consider the issue of the degree of correspondence between the model and real temperature distributions.

From Figs. 5c and 5d it can be seen that the temperature distribution in the vortices obtained within the framework of the model does not correspond to the results of numerical simulation, namely, the temperature in the vortex core is appreciably lower than that predicted by the model at large \(k\) (in accordance with (2.3), at the centers of vortices the temperature must have a local maximum). This fact leads to the difference between the distributions of \({{i}_{0}}\) in Figs. 5a and 5b. In the space between the vortices the difference is less significant.

We will consider the basic mechanisms that determine the temperature of vortices in the near wake. Variation in the temperature \(T\) in fluid particles can be described by the equation

$$\frac{{dT}}{{dt}} = - p\frac{d}{{dt}}\left( {\frac{1}{\rho }} \right) + \frac{1}{{\rho {\text{Re}}}}{\boldsymbol{\tau }}:\nabla {\mathbf{u}} + \frac{\gamma }{{\rho {\text{RePr}}}}{{\nabla }^{2}}T,$$
(2.5)

where the first two terms on the right-hand side correspond to the work of the internal surface pressure and friction forces (the first and the second terms, respectively); the third term describes variation in the temperature as a result of heat conduction. The sum of the first two terms determines transitions between the internal energy (in dimensionless variables it coincides with the temperature) and the kinetic energy. The kinetic energy \(K = {{({{u}^{2}} + {{{v}}^{2}})} \mathord{\left/ {\vphantom {{({{u}^{2}} + {{{v}}^{2}})} 2}} \right. \kern-0em} 2}\) can additionally change due to the work done by the external pressure and friction forces (the sum of the first two terms and the fourth term, respectively)

$$\frac{{dK}}{{dt}} = \frac{1}{\rho }\frac{{\partial p}}{{\partial t}} - \frac{d}{{dt}}\left( {\frac{p}{\rho }} \right) + p\frac{d}{{dt}}\left( {\frac{1}{\rho }} \right) + \frac{1}{{\rho {\text{Re}}}}\left( {\nabla \cdot {\boldsymbol{\tau }}} \right) \cdot {\mathbf{u}}.$$

Two factors determine the temperature in the forming vortices. The first factor is gas heating in the neighborhood of the body surface due to the work of the internal forces (primarily, the friction forces); the second factor is gas cooling in the vortex formation region in which the density decreases significantly (and, consequently, the temperature also decreases in accordance with the first term on the right-hand side of Eq. (2.5)). Since at small \(k\) (\(k \leqslant 0.5\)) we have the body of a more streamlined shape, the density behind it varies only slightly and the higher temperature is observed in the vortices (Figs. 2c and 5c). At large \(k\) (\(k > 1.0\)) gas is considerably rarefied, the temperature of vortices reduces during vortex formation. For example, in the numerical calculations at \(k = 0.1\) the maximum density decrease is equal to approximately 5%, whereas at k = 10 in the vortex cores it can be greater than 40%. Within the framework of the model described above, at the center of vortices the maximum density

$${{\rho }_{{{\text{max}}}}} = \mathop {\left( {1 + \frac{{\gamma - 1}}{2}M_{\infty }^{2}{{U}^{2}}} \right)}\nolimits^{1/(\gamma - 1)} $$

is reached.

We will consider the temperature distribution in the vortices distinguished in Fig. 5 in more detail. In Fig. 6 we have plotted the temperature and absolute value of the velocity V (in the coordinate system moving with the vortex) in the vortex cross-sections \(x = {{x}_{0}}\) and \(y = {{y}_{0}}\), where \(({{x}_{0}},{{y}_{0}})\) are the coordinates of the vortex center. Inside the vortex cores, the dependence of the velocity V on the distance from the center \(({{x}_{0}},{{y}_{0}})\) is close to the linear one (Figs. 6a and 6b). In this region a qualitative difference of the temperature distribution appears at \(k \geqslant 1\) (Figs. 6c and 6d): within the framework of the model it increases, in calculations the core has the lower temperature as compared with the surrounding medium. However, at \(k = 0.5\), as in the model, there is a local maximum at the center of vortex. As mentioned above (Subsection 2.2), in constructing the model we can assume that in the vortex cores the static temperature is constant. Such an assumption is in a better agreement with the numerical experiment only at \(k \geqslant 1\), although, as can be seen from Figs. 6c and 6d, at large \(k\) it also leads to the overestimated temperature values (within the framework of the modified model the temperature must be equal to the temperature on the core boundary).

Fig. 6.
figure 6

Velocity and temperature distributions in the vortex cores. The cross-sections of the vortices marked by heavy dashed curves in Fig. 5 and the lines \(x = {{x}_{0}}\) (b, d) and \(y = {{y}_{0}}\) (a, c) are given. Here, \(({{x}_{0}},{{y}_{0}})\) are the coordinates of the center of the vortex; (a, b) correspond to absolute value of the velocity in the coordinate system moving with the vortex; (c, d) correspond to temperature \(T - {{T}_{\infty }}\) obtained in solving the Navier–Stokes equations (black curve) and calculated from formula (2.3) (thin red curve).

Full size image

The results of numerical calculations (Figs. 5c and 6) show that in the vortex cores the temperature can both increase and decrease. This is determined by the flow in the vortex formation region. This fact is not taken into account in the considered model based on the velocity field in the developed wake. Therefore, the assumption on the temperature distribution in the vortex core that leads to Eq. (2.3) turns out to be rough.

Thus, we should expect that the predictions for \({{i}_{0}}\) in the near wake behind the bluff body with the use of simplified model will be overestimated since the model neglects an additional vortex cooling in the process of vortex formation. For “wide” wakes the estimate of the energy separation intensity will be more accurate because the temperature distribution is in good agreement with calculations in space between the vortices in which the minimum of \({{\bar {i}}_{0}}\) is reached.

SUMMARY

The process of redistribution of the total enthalpy in the wake behind cylindrical bodies of various cross-sections in viscous perfect gas flow is investigated based on numerical solution of the Navier–Stokes equations at \({\text{Re}} = 1000\), \({{{\text{M}}}_{\infty }} = 0.4\), and Pr = 0.72.

In the case of bluff bodies the total enthalpy is more intensively redistributed in a time-averaged flow: the local minimum of \(\overline {{{i}_{0}}} \) decreases and the size of the region of significantly reduced \(\overline {{{i}_{0}}} \) increases. In the flow past an elliptic cylinder with the transverse-to-longitudinal-dimension ratio \(k = 10\) we obtain reduction in the minimum value of \(\overline {{{i}_{0}}} \) (reached in the vortex formation region) by 6.9% as compared with the free-stream value. For the circular cylinder (\(k = 1\)) this value is equal to 4.8%, while it is equal to only 0.6% at \(k = 0.1\). At \(k = 10\) the area of the region of significantly reduced \(\overline {{{i}_{0}}} \) increases considerably in the developed wake with the minimum equal to 4.7%.

The intensification of \(\overline {{{i}_{0}}} \) redistribution in the developed wake is attributable to the more intensive decrease in the kinetic energy in the central part of the wake due to the increase in circulation of shedding vortices and the transverse distance between them, as well as significant rarefaction in the vortex formation region. This leads to the reduction in the temperature of the vortices shedding to the stream.

The simplified model that makes it possible to estimate the intensity of redistribution of the total enthalpy \({{i}_{0}}\) in the developed near wake from the velocity field is considered. The results obtained are in qualitative agreement with the numerical calculations. The shortcoming of the model is the neglect of redistribution of \({{i}_{0}}\) in forming the vortices. This process significantly affects the gas temperature in the vortex cores in the near wake which can be both higher and lower than the free-stream static temperature. For the bluff bodies this leads to overestimating the values of \({{i}_{0}}\) predicted by the model.