Hysteresis in Supersonic Flow Past a Plane Cascade of Cylindrical Rods

Abstract—

The results of numerical simulation of the interaction of supersonic flow with a permeable screen in form of an infinite plane cascade (lattice) of circular cylinders are given. The interaction regime in which the shocks ahead of the cylinders are localized on the scale of the cascade step is considered. The multi-block computational technique in which the viscous boundary layers are resolved by means of local grids using the Navier–Stokes equations, while the effects of inteferrence between the shock-wave structures in supersonic wake are described within the framework of Euler’s equations. The action of shock waves induced by the neighboring elements of lattice to the near-wake region behind the intermediate elements can ambiguously affect the aerodynamic lattice performance as well as generate time-dependent phenomena in the wake. The flow regimes are classified depending on continuous increase and decrease in the free-stream supersonic air flow in the Mach number range from 2.4 to 4.2 with reference to the lattice of the 80% permeability. The sources of the hysteresis behavior of the lattice aerodynamic drag with respect to the Mach number and the mechanisms of the onset of self-oscillating wake flow regimes are discussed.

Supersonic flow past permeable screens (grids, perforated plates, lattices and so on) is of interest in many technological applications [1–5], as well as in the problems of analysis of certain natural phenomena such as gas dynamics of splintering of disintegrating meteoroids and other [6‒8]. The formulation of the adequate boundary conditions on the surfaces of a strong gas dynamic discontinuity that simulate the permeable screens [9, 10] is of fundamental value. In the case of fairly permeable screens located transversely supersonic stream, the flow takes place without formation of global stand-off shock wave [2, 5, 10]. A very simple model of the permeable screen is the plane cascade (lattice) of parallel circular cylinders located at an identical distance from each other. In this case the flow past a permeable screen can be described in detail on all scales–from the local dimension of lattice elements to the global dimension of screen [11–13]. In the regime without stand-off bow shock ahead of the screen the perturbations from the windward side of lattice are limited by the fronts of local shock waves ahead of the rigid lattice elements, while a discrete system of small supersonic jets develops on the leeward side. These jets close up gradually and form the secondary supersonic stream behind the latticed screen [10]. In accordance with classification in [9, 10], this is the regime E3 for which the boundary condition on the permeable surface can be represented as an algebraic relation between the Mach numbers of supersonic streams upstream and downstream of the surface of strong discontinuity that simulates the lattice. In such a regime the general lattice dimension has no value and the lattice can be considered as an infinite permeable screen [11]. In this case, to describe flow on the scale of the lattice step the attention can be restricted to calculations in the strip that contains a single cylindrical element, so that the boundary conditions of periodicity of flow should be fulfilled on the parallel side faces of the strip [12].

The investigations [11, 12] showed that complex shock-wave flow structures develop in the near-wake region behind the cylindrical lattice elements. In these structures the shock waves propagating from the neighboring lattice elements interact between themselves and with inhomogeneous domains of the near aerodynamic wake. In this case, the ambiguity of the structure of such flows and the corresponding parametric hysteresis are possible under certain combinations of the problem parameters when the characteristics of flow past the lattice depend on not only the values of constitutive parameters but also on the prehistory of establishing the values of these parameters. In [11] the hysteresis related to the well-known ambivalence of the possible schemes of intersection of shock waves in accordance with the Mach-type or regular interaction was described. In [12] a new type of hysteresis related to restructuring of the near wake behind the lattice as a result of the action of shock waves from the neighboring elements directly to the rear flow region behind intermediate lattice element was identified. Recently, the time-dependent flow regimes with formation of a discrete vortex street in the supersonic wake behind the lattice were reported [13, 14]. In the present study supersonic air flow past a periodic lattice of 80% permeability is investigated as a function of continuously increasing and decreasing free-stream Mach number in the range of 2.4–4.2. The reasons of ambiguous dependence of the flow structures in the wake on the Mach number of supersonic free stream and the corresponding parametric resonance as well as the mechanisms of the development of time-dependent flow regimes in the wake are discussed.

FORMULATION OF THE PROBLEM AND THE NUMERICAL MODEL

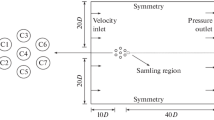
We will consider the interaction between uniform supersonic flow of a viscous perfect gas and an infinite permeable screen in the form of a plane periodic lattice of parallel cylindrical rods. The plane of lattice is perpendicular to the free-stream supersonic velocity vector V₁. The gas specific heat ratio γ = 1.4. The Reynolds number calculated on the basis of the undisturbed stream parameters and the diameter D of the cylindrical lattice element is equal to Re = 10⁵. The free-stream Mach number M₁ is varied from 2.4 to 4.2. The lattice period h = 5D ensures the fairly high degree of the screen permeability σ = 1 – D/h = 0.8 for which the shock waves ahead of the lattice elements remain local and do not form a global bow shock ahead of the permeable screen [12]. In this case a secondary supersonic stream which is the result of confluence of discrete small jets formed between the lattice elements is formed behind the screeen [2, 10].

Gas flow is described by the system of two-dimensional Navier–Stokes equations with the no-slip boundary conditions on the isothermal surface of the lattice elements. The solution is constructed numerically in the strip of width h between two longitudinal planes on which the condition of periodicity of the solution in the transverse coordinate Y is imposed. A single lattice element is located inside the strip (Fig. 1a).

Fig. 1.

Computational domain and coordinate system (a); structure of computational grids (b) with finite overlapping (c).

The results of comparative calculations [13] of flow past a system of elements of finite lattice and flow past a single element with the periodicity conditions for the infinite rare lattice confirm the absence of qualitative differences; in particular, the diversity of flow diagrams past the infinity lattice is conserved. In this case the boundary condition of periodicity makes it possible to improve the resolution of the computational grid.

The inlet boundary of the computational domain is located in the undisturbed stream with the Mach number M₁ ≥ 2.4. The outflow boundary is located far downstream in the supersonic wake region and the free-outflow boundary conditions are imposed here. In what follows, all linear elements in the flow region are normalized using the radius of a lattice element, in particular, D = 2.

When γ = 1.4 and σ = 0.8 the necessary condition of existence of a steady-state supersonic flow ahead of the infinite lattice [12]

$${{\sigma }^{2}} > \frac{{2 + (\gamma - 1){\text{M}}_{1}^{2}}}{{(\gamma + 1){\text{M}}_{1}^{2}}}{{\left( {\frac{{2\gamma {\text{M}}_{1}^{2} + 1 - \gamma }}{{(\gamma + 1){\text{M}}_{1}^{2}}}} \right)}^{{\frac{2}{{\gamma - 1}}}}}$$

reduces to the condition M₁ > 2.15. In accordance with calculations [11], transition from the regime with the branching system of local shock waves ahead of the lattice elements to the regime with the smooth stand-off occurs in the interval 2.35 < M₁ < 2.4. These facts were taken into account in choosing the lower boundary M₁ = 2.4 of variation in the parameter M₁ in the present study. The upper boundary M₁ = 4.2 was chosen from the condition of absence of the alternative to the scheme of regular intersection of the bow shocks initiated by the neighboring cylindrical lattice elements [11]. When M₁ > 4.2 the angle 2α of regular intersection of these shocks is smaller than the theoretical limit 2α_N of existence of the triple Mach configuration at this point. Here, α_N = f(M₁, γ) is the Neuman angle [15, 16].

The solution of the formulated boundary-value problem can be constructed by means of the multi-block computational technique [7, 12, 17] using local curvilinear grids “B” adapted to the body surface. These grids have finite overlapping domains with the global rectilinear grid “A” for the entire computational domain (Figs. 1b and 1c). The viscous boundary layers are resolved using the Navier–Stokes equations on grids condensed to the body surfaces, while the effects of inteference between the shock-wave structures in the supesonic wake are descrtibed within the framework of Eulers’s equations. Function interpolation to the boundaries of transition from a grid to another one is used in the grid overlapping domains. In [17] the mathematical model and the integration method are described in detail. In the basic series of present calculations the step of the global grid “A” (Fig. 1) was equal to 0.0125 (in fractions of the radius of cylindrical lattice element); the minimum step of the local grid “B” was equal to 0.0005 in the neighborhood of the boundaries of lattice elements; and the totasl number of conputational nodes amounted to 3 270 000. The test and check computations were caried out using the grids of the density that is lower and higher by two times.

Tactics of successive variation in the Mach number M₁ [11, 12] on the inlet boundary of the computational domain were used for diagnostics of the possible hysteresis regimes. In this case the solution from the previous small step in M₁ was taken as the initial gas dynamic field. The isolines of the Mach numbers, the pressure, and the absolute value of the density gradient, as well as the characteristic streamlines were computated to visualize the resulting flow fields in the neighborhood of the lattice. The coefficients С_x and С_y of the aerodynamic force acting on a lattice element were determined by integrating the pressure over the surface of this element. The differences between С_x and the values of the drag coefficient C_x0 of a single cylinder in infinite supersonic flow characterize the effect of aerodynamic interference between the lattice elements. The calculated values of C_x0 obtained in the interval 2.4 ≤ M₁ ≤ 4.2 can be fairly adequately described by the approximation dependence C_x0 = 1.39 – 0.097 ln(M₁ – 1).

CALCULATION RESULTS

In Figs. 2a and 2b we have reproduced the flow patterns of M₁ at the ends of its interval of variation (density of shades of grey is proportional to the absolute value of the gas density gradient). At M₁ = 4.2 the perturbations from the neighboring lattice elements interact between each other in the supersonic part of the aerodynamic wake and do not affect neither the shock layer ahead of the cylinder nor the near wake (Fig. 2a). The bow shock ahead of the cylinder and the main part of the near wake are the same as those in flow past the cylinder in unbounded supersonic flow. The aerodynamic drag coefficients of lattice elements and a single cylinder are identical: C_x = C_x0 = 1.277. A complex shock-wave structure is formed in the supersonic flow region behind the lattice. Initially, the bow shock waves “1” induced by the neighboring elements intersect each other and the rear shocks “2” in accordance with the regular interaction scheme and thereafter they form the triple Mach-type configuration in the supersonic wake region behind the intermediate lattice element (Fig. 2c). In this case a local secondary subsonic region is formed behind the Mach stem “3” in the neighborhood of the wake axis and the departing branch of the triple Mach-type configuration “4” overtakes the refracted front “5” of the rear shock and merges with it by forming the supersonic λ-configuration of shocks with a weak contact discontinuity [18]. It should be noted that in calculations [11] the attention was focused only to the zones of primary interaction of bow shocks going out from the neighboring lattice elements and the further variety of secondary shock-wave interactions behind the lattice was not reproduced and studied. In particular, the separated base flow and the rear shocks in the near wake behind the lattice elements could not be obtained without regard for gas viscosity. Accordingly, the cellular shock configuration in the supersonic wake was not reproduced (Fig. 2a).

Fig. 2.

Visualization patterns of the computational fields of absolute value of the density gradient at М₁ = 4.2 (a) and М₁ = 2.4 (b); main structural elements of flow (c).

Significantly different pattern can be observed at M₁ = 2.4 (Fig. 2b). The bow shocks from the neighboring lattice elements intersect in accordance with the Mach-type interaction with formation of clearly expressed Mach stem. In this case the reflected shock waves directly act on the subsonic region of the near wake leading to almost three-fold increase in its dimensions and considerable increase in the base pressure on the lattice elements. At M = 2.4 the corresponding value of the aerodynamic drag coefficient of the lattice element C_x = 1.02 is significantly smaller than C_x0 = 1.36 for a single cylinder.

In both cases for the values of M₁ on the ends of its interval of variation the flow of interaction between the supersonic stream and the lattice (Fig. 2) is uniquely determined by the Mach number M₁ (Fig. 2). However, inside the interval 2.4 < M₁ < 4.2 there exist regions of the ambiguous dependence of flows on this parameter.

In Fig. 3 we have reproduced two different regimes of flow past the lattice at the same Mach number М₁ = 3.2 but for different prehistory of establishing this value. In Fig. 3a the flow was obtained in accordance with the scenario with gradual decrease in М₁ starting from М₁ = 4.2. In general outline, it is similar to the steady-state flow shown in Fig. 2a. The perturbations from the neighboring lattice elements have no effect on in near flow field. Therefore, all basic characteristics of flow past lattice elements and a single cylinder in unbounded flow coincide. In particular, such features as the structure of the subsonic region of near wake and the value of the aerodynamic drag coefficient (in our case C_x = C_x0 = 1.31) coincide. As opposed to this, in Fig. 3b the flow was obtained by gradually increasing М₁, starting from М₁ = 2.4. On this way, transition from the steady-state to the time-dependent flow regime in the aerodynamic lattice wake takes place. The secondary shocks from the neighboring lattice elements interact with the inhomogeneous transonic near-wake region; as a result, suspended sepaeration structures develop; in turn, these structures interact with the subsonic part of the near wake. This complex interaction has the clearly expressed unsteady nature. The aerodynamic drag and the lift force of a lattice element perform quasi-periodic oscillations. The mean value of the drag coefficient C_x = 1.25 is considerably smaller than the value of C_x0 = 1.31 for a single cylinder.

Fig. 3.

Visualization of the computational fields of absolute value of the density gradient at М₁ = 3.2 calculated in accordance with the scenarios with decrease in М₁ starting from 4.2 (a) and with increase in М₁ starting from 2.4 (b).

Figure 4 illustrates the ambiguity of the lattice flow regimes at М₁ = 2.6. In Fig. 4a the flow was obtained by means of gradual increase in the Mach number starting from М₁ = 2.4. Flow is similar to the steady-state flow shown in Fig. 2b. In the case of the irregular interaction between the bow shocks initiated by the neighboring lattice elements, the reflected shocks in the triple Mach-type configuration directly act on the subsonic near-wake region leading to increase in its dimensions and growth in the base pressure on the lattice elements. In this case the resultant flow remains to be steady-state and the aerodynamic drag coefficient of the lattice element C_x = 1.03 is much smaller than the value of C_x0 = 1.34 for a single cylinder at M₁ = 2.6. As opposed to this, in Fig. 4b the flow was obtained by means of gradual decrease in the Mach number. Flow has the clearly expressed unsteady nature in which the aerodynamic drag C_x and the lift force C_y of a lattice element perform quasi-periodic oscillations. On the graph of oscillations of C_y (Fig. 4c) we have plotted the quantity i = 0.01t/Δt, which corresponds to the number of hundreds of time steps Δt during the numerical simulation. In this case the mean value of C_x = 1.25 remains smaller than the drag coefficient C_x0 = 1.34 of a single cylinder.

Fig. 4.

Visualization of the computational fields of absolute value of the density gradient at the Mach number М₁ = 2.6 calculated in the scenarios with increase in М₁ starting from 2.4: the steady-state regime (a) and with decrease in М₁ from 4.2: the non-stationary regime (b); oscillations of the lift coefficient of a lattice element in the non-stationary regime (c).

The ratio C_x/C_x0 characterizes the contribution of the effects of aerodynamic interference to the lattice aerodynamic drag. In Fig. 5a we have constructed the calculated data obtained in accordance with the scenarios of continuous increase and de crease in the Mach number M₁ in the interval from 2.4 to 4.2. The dependence C_x/C_x0 = f(M₁) is disintegrated into three isolated branches. The lower branch I corresponds to the steady-state flow regimes as those shown in Figs. 2b and 4a. In this lower regime the aerodynamic drag of an element inside the lattice is smaller by 20–27% than the drag of a single element in unbounded flow. The upper branch III corresponds to the steady-state flow regimes as those shown in Figs. 2a and 3a. In the upper regime the aerodynamic drag of a lattice element and the drag of the same single element in unbounded flow coincide. The intermediate branch II corresponds to the unsteady flow regimes similar to those shown in Figs. 3b and 4b. Transitions from one branch to another occur in the threshold way as shown by arrows in Fig. 5a. Clearly, there are two hysteresis loops and, accordingly, two intervals of the values of the parameter M₁, for which the solution of the problem of flow past the lattice is not single-valued. The selection of one of the possible flow regimes in the non-uniqueness intervals is determined by not only a particular value of the parameter M₁, but also the prehistory of establishing this value. This property of ambiguity of the solution is the reason of the hysteresis behavior of the dependence of C_x/C_x0 on M₁.

Fig. 5.

Classification of regimes I, II, and III of flow past the lattice: hysteresis calculated dependence of C_x/C_x0 on M₁ (a); indicator К = f(M₁) calculated from formula (2).

If the lattice together with the neighboring layer of inhomogeneous dissipative flow is interpreted as the surface of strong gas dynamic discontinuity, then the drag coefficient of unit lattice area C_x1 can be calculated from the theoretical formula [9]

$${{C}_{{x1}}} = \frac{{\gamma + 1}}{\gamma }\left( {1 - \frac{{{{\lambda }_{2}}}}{{{{\lambda }_{1}}}}} \right)\left( {1 - \frac{1}{{{{\lambda }_{2}}{{\lambda }_{1}}}}} \right),$$

(1)

where

$${{\lambda }_{{1,2}}} = {{{\text{M}}}_{{1,2}}}{{\left( {\frac{{\gamma - 1}}{{\gamma + 1}}{\text{M}}_{{1,2}}^{2} + \frac{2}{{\gamma + 1}}} \right)}^{{ - 1/2}}},$$

and M₁ and M₂ are the Mach numbers ahead of and behind the surface of discontinuity.

The calculated gas dynamic fields were used to determine the values of gas dynamic flow parameters averaged over the periodicity strip width (Fig. 1). The ratio of the drag coefficient of permeable surface (1) to the actual drag coefficient of the lattice (1 – σ)C_x

$$K = \frac{{{{C}_{{x1}}}}}{{(1 - \sigma ){{C}_{x}}}}$$

(2)

characterizes the accuracy of the permeable surface model [9] with reference to the lattice of cylindrical rods. In Fig. 5b we have reproduced the calculated dependence K = f(M₁) for the steady-state flow regimes I and III shown in Fig. 5a. In calculating C_x1 from formula (1), we used the averaged calculated Mach number M₂ in the cross-section X = 20 in the lattice wake, while in calculating the drag coefficient C_x of a lattice element the actual calculated pressure on the surface of this element was used. The small deviation of the parameter (2) from 1 characterizes the high accuracy of formula (1) in the steady-state regimes of flow past the lattice. In the case of time-dependent regimes II (Fig. 5a) the question of simulation of a lattice using the surface of gas dynamic discontinuity remains open.

In Fig. 6 we have reproduced the fields of the Mach number M when the values of M₁ decrease successively with transition from the stationary state of flow on the upper branch III of the curve C_x/C_x0 = f(M₁) to the non-stationary state on the intermediate branch II (Fig. 5a).¹ At M₁ = 4.0 the Mach-type interaction of the secondary shocks in the supersonic part of wake generates the subsonic region (Fig. 6a). This subsonic region increases with decrease in M₁ (Fig. 6b). In this case the presence of the local minimum Mach number in the core of inhomogeneous supersonic wake behind the lattice element generates a precursor in the form of local projection on the shock front that intersects the axis of this wake (Fig. 6b). As M₁ decreases, the precursor grows rapidly and penetrates into the near-wake region behind the lattice element (Fig. 6c). As a result, a long subsonic «tongue» that interacts with reflected and refracted shock waves in adjacent supersonic flow regions is formed. Instability and oscillations of this complex shock-wave and selected structure (Fig. 6d) are the reason of formation of a time-dependent system of vortex bunches that drift downstream along the supersonic wake behind the lattice (Fig. 3b). Figure 7 illustrates the details of the corresponding self-oscillating process. In this figure the time-dependent shock-wave configurations and the subsonic zones (M < 1) are visualized² for the approximately half-period of self-oscillations in successive instants of time with the step of 500Δt (Δt is the dimensionless time step in the calculation).

Fig. 6.

Fields of the Mach number M calculated in the scenario with successive decrease in the parameter М₁ from 4.0 (a) to 2.8 (d).

Fig. 7.

Oscillations of the near wake at М₁ = 2.8: (a– f) correspond to instantaneous level lines of the Mach number M at successive instants of time in step of 500Δt.

DISCUSSION OF THE RESULTS

Three principal mechanisms determine complexity of the interaction of supersonic flow and the rare lattice that does not give rise to flow chocking and appearing of the stand-off shock wave.

The first mechanism is the action of local shocks initiated by the neighboring lattice elements directly to the base separation region of the near wake behind the intermediate elements (similar to that shown in Fig. 2b). As a result, the dimensions of the base region increase considerably and the base pressure on the lattice elements also increases. The ambiguity of the flow structure related to this mechanism and the corresponding parametric hysteresis appear in those cases in which the above-mentioned local shocks are displaced downstream so much that they pass by the short undisturbed base region but are not able to fall into the preliminarily disturbed increases base region. In the present study such a hysteresis is identified in accordance with the parameter M₁. In [12] a similar hysteresis was revealed in varying the distance between the lattice elements at fixed M₁ = 6. Obviously, the same mechanism can lead to hysteresis with respect to other problem parameters including the specific heat ratio and the Reynolds number. The same mechanism can be the cause of parametric hysteresis of characteristics of supersonic plow past not only the lattice but also past other systems of bodies.

The second mechanism relates to existence of the interval of ambiguity of the schemes of intersection and reflection of shock waves from the neighboring lattice elements. Variation in the Mach number M₁ leads to variation of the angle of inclination and the intensity of shocks on the axis of symmetry between the lattice elements. There exists a known range of these parameters in which reflection of shock waves can occur in accordance with the scheme of both the regular and the Mach-type interaction [15, 16]. The hysteresis of shock-wave configurations between lattice elements determined by this mechanism is described in [11].

The third mechanism is the formation of a precursor of supersonic wake behind the lattice element during the interaction of reflected shock waves with the core of wake inhomogeneity (similar to that shown in Figs. 6b and 6c). The presence of the core of transverse inhomogeneity in supersonic flow similar to the local minimum of the Mach number is the well-known cause of the development of a precursor in the form of a separation structure projected upstream in the zone of intersection of the shock wave and the core of inhomogeneity [19]. The corresponding time-dependent analog is the appearance of a precursor ahead of the shock front propagating along the local reduced-density channel in a gas at rest [20]. Penetration of the precursor into the near-wake region behind the lattice element leads to the formation of an extended subsonic channel (Fig. 6c) through which the separated base region interacts with the shock-wave structures in the supersonic part of the wake. Instability of such a configuration generates self-oscillations (Figs. 6d and 7) accompanied by the formation of discrete street of vortex bunches drifting in the supersonic wake (Fig. 3b).

The simultaneous action of the second and third mechanisms can lead to secondary hysteresis phenomena. This relates to the fact that transition from the regular to Mach-type reflection takes place with sudden formation of the Mach stem of finite height. This leads to jump-wise displacement (towards the lattice) of reflected shock waves that interact with the aerodynamic wake. In particular, for the lattice of 80% permeability such a transition is inevitable when M₁ decreases from 3.2 to 3.1 due to reaching the theoretical limit in the angle of rotation of the stream in accordance with the scheme of regular reflection of shocks in this interval [16]. Regular reflections of shocks at M₁ = 3.15 represented in Fig. 6c are close to this limiting state. Further decrease in M₁ leads to sudden appearance of triple shock configurations with the Mach stem of finite height (Fig. 6d). However, the reverse motion in the parameter M₁ towards increase does not leads to restoration of the scheme of regular reflection at M₁ = 3.15. As M₁ increases, the dimensions of the Mach stem gradually decrease to zero. In [11] this process was investigated in detail by means of special measures on refinement of the computational grids in the neighborhood of the point of reflection.

It should be also noted that the interaction of reflected shock waves with rear shocks and between each other can also occur in accordance with the schemes of Mach-type or regular reflection. In turn, this can affect the conditions of their interaction with the core of inhomogeneous flow in the wake. In part, this can lead to multiple parametric hysteresis in flow past lattices and systems of bodies. A certain spread of the points on the mean branch II of the regime curve obtained in the present calculations (Fig. 5a) can be explained by manifestation of secondary hysteresis.

SUMMARY

The flow regimes developed as the air free-stream Mach number continuously increases or decreases in the range from 2.4 to 4.2 are classified with reference to supersonic flow past an infinite lattice of cylindrical rods of the 80% permeability. The action of shock waves from the neighboring lattice elements on the region of near aerodynamic wake behind the intermediate elements generates both ambiguous flow structures and time-dependent phenomena in the wake. Three basic flow regimes (lower, intermediate, and upper regimes I, II, and III in Fig. 5a) are identified and the mechanisms that determine the variety of the corresponding wake flows including the manifestation of parametric hysteresis in transition from one to another regime are explained. The interpretation of the lattice as the surface of gas dynamic discontinuity gives the functional dependence between the drag coefficient and the Mach numbers of average supersonic streams on both sides of the permeable screen. The results of present calculations confirm the high accuracy of such a simulation in the case of steady-state regimes I and III (Fig. 5b).