Pulsating Flow of a Viscous Fluid over a Cavity Containing a Compressible Gas Bubble

A two-dimensional pulsating flow of a viscous fluid in a plane channel whose wall has rectangular microcavities partially or completely filled with a compressible gas is investigated. This problem formulation can clarify the friction reduction mechanism in a laminar sublayer of a turbulent viscous boundary layer flow over a textured stripped superhydrophobic surface containing periodically arranged rectangular micro-cavities filled with gas. It is assumed that the dimensions of the cavities are much smaller than the channel thickness. On the macroscale, the problem of one-dimensional unsteady viscous flow in a plane channel with no-slip conditions on the walls and a harmonic variation of the pressure difference is solved. The solution obtained in this way is used for formulating non-stationary in time and periodic in space boundary conditions for the flow on the scale of a chosen cavity (microscale), with the instantaneous volume of the gas bubble in the cavity depending on the instantaneous pressure over the cavity. The flow on the microscale near a cavity with a gas bubble occurs in the Stokes regime. The numerical solution is obtained using an original version of the boundary element method. A parametric numerical study of the flow field in a pulsating shear flow over a cavity with a compressible gas bubble is performed. The averaged parameters characterizing the effective ‘velocity slip’ of viscous fluid and the friction reduction in a pulsating flow over a stripped superhydrophobic surface are calculated.

Surfaces with a structured roughness (texture) in combination with chemical hydrophobicity are called superhydrophobic surfaces. When such a surface is immersed in a viscous-fluid flow, in the roughness elements (microcavities) gas microbubbles can be trapped by the surface tension force. This state of the surface is called the Cassie state [1]. Since there is almost no friction on the bubble boundary, an averaged (macroscopic) velocity slip of the fluid and a noticeable decrease in the averaged friction occur on the superhydrophobic surface. For practical purposes, the problem of optimizing the texture of superhydrophobic surfaces in order to minimize the friction in viscous-fluid flows over such surfaces is of interest. The need in solving this problem supports the interest in a parametric numerical study of viscous-fluid flows along superhydrophobic surfaces. As a rule, the characteristic dimensions of the microcavities of superhydrophobic surfaces do not exceed fractions of a millimeter, so the local flow over a cavity is characterized by small Reynolds numbers. Researches consider mainly the textures formed by a periodic system of infinite rectangular microcavities completely occupied by a gas or other low-viscosity fluid, with the shape of the phase interface assumed to be known and given. For a flat phase interface and periodic boundary conditions on the scale of a single cavity, within the Stokes approximation the solution of this problem can be obtained by expanding it into a Fourier series or using the theory of functions of a complex variable [2–5]. However, the values of the effective slip length and the friction reduction calculated under such assumptions are much higher than those in the available experimental measurements. Experimental observations of the flow on the cavity scale show that usually the bubble surface is curved, and the cavity can be only partially filled with gas, i.e., the position of the meniscus may not coincide with the upper corner points of the microcavity. These factors were taken into account in the studies of a steady flow over cavities with gas bubbles in [6–8], where an original version of the boundary integral equation method for the Stokes operator was developed, taking into account the alternating boundary conditions (no-slip/zero friction) on the boundaries of the computational domain. Both the shape of the meniscus and its location relative to the cavity corner points affect very substantially the parameters characterizing the average fluid velocity slip and the friction reduction. In recent years, in the literature there appear numerical calculations of flows near microcavities with account for not only a meniscus curvature but also a deformation of the phase interface, different geometries of the cavity, and different ratios of the viscosities of the outer flow and the fluid filling the cavity [9–10]. Accordingly, it may be concluded that the factors influencing the friction reduction effect in steady-state laminar flows along superhydrophobic surfaces have been studied in sufficient detail. However, for unsteady and turbulent flows along superhydrophobic surfaces the possible friction reduction mechanisms are still not well understood, although there exist experimental confirmations of a noticeable reduction of the friction on a superhydrophobic surface in a turbulent flow [11]. In attempts to model numerically turbulent flows in channels with superhydrophobic walls, it is common to specify the Navier slip boundary conditions for the velocity (the proportionality of the average slip velocity to the vertical gradient of the longitudinal velocity on the wall). In doing this, to get a substantial variation of the turbulent friction on the wall in the calculations, it is necessary to specify fairly large values of the ‘velocity slip length’, which are greater than the similar values for steady laminar flows. In [12], it was revealed that in a turbulent flow in a circular pipe a longitudinal velocity slip results in a drag reduction, while a velocity slip in the transverse direction, on the contrary, increases the friction on the pipe walls. In the literature, there are attempts to model directly the boundary conditions on a superhydrophobic wall by altering small segments of no-slip and zero-shear-stress conditions on the microscale [13]. However, to the authors’ knowledge, for a laminar sublayer of a turbulent flow the effect of velocity and pressure fluctuations on the behavior of gas bubbles in microcavities of a superhydrophobic surface and, as a result, on the value of average velocity slip has not been studied. An exclusion is the authors’ short note [14] in which a shear flow over a plane rectangular cavity with a gas bubble pulsating under the action of a harmonic pressure variation over the cavity was considered. In [14] it was demonstrated that in the presence of pressure fluctuations under certain conditions the average slip of the fluid over the cavity can be greater and the friction lower than in a similar steady-state flow.

In the present study, the problem formulation of [14] is substantially complicated by the account for fluctuations of the longitudinal fluid velocity over the cavity, which better matches real conditions in the near-wall region of a turbulent flow over a stripped superhydrophobic surface.

1 PULSATING FLOW IN A PLANE CHANNEL

For certainty, as the external flow over a cavity with a gas bubble we will consider a pulsating flow of a viscous fluid in a plane channel with width H* in Cartesian coordinates x*, y*, where the x*-coordinate is directed along the lower channel wall. The asterisk here and below denotes dimensional variables.

In dimensional form the equations of one-dimensional unsteady flow read:

$$\rho {\text{*}}\frac{{\partial u{\text{*}}}}{{\partial t{\text{*}}}} = - \frac{{\partial p{\text{*}}}}{{\partial x{\text{*}}}} + \mu {\text{*}}\frac{{{{\partial }^{2}}u{\text{*}}}}{{\partial {{y}^{{{\text{*}}2}}}}},\quad \frac{{\partial p{\text{*}}}}{{\partial y{\text{*}}}} = 0,\quad \frac{{\partial u{\text{*}}}}{{\partial x{\text{*}}}} = 0.$$

(1.1)

Here, u* is the longitudinal velocity, p* is the pressure, and μ* is the dynamic viscosity. From the second equation it follows that p* = p*(t*, x*). It is assumed that the pressure drop in the channel varies in accordance with the monochromatic law, so that the longitudinal pressure gradient takes the form

$$\frac{{\partial p{\text{*}}}}{{\partial x{\text{*}}}} = - K{\text{*}} - A{\text{*}}\sin \omega {\text{*}}t{\text{*}}{\text{.}}$$

Here, K* is the modulus of the pressure gradient in the absence of the pressure fluctuations, and A* and ω* are the amplitude and the frequency of the pressure fluctuations. The following dimensionless variables are introduced: (x*, y*) = (xH*, yH*), p* = pH*K*, u* = uU*, and t* = t/ω*. The velocity scale U* corresponds to the channel flow in the absence of pressure fluctuations: U* = K*H*²/μ*. In dimensionless form the equations of motion read:

$$\begin{gathered} B\frac{{\partial u}}{{\partial t}} = 1 + A\sin (t) + \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}},\quad \frac{{\partial u}}{{\partial x}} = 0, \\ A = \frac{{A{\text{*}}}}{{K{\text{*}}}},\quad B = \operatorname{Sh} \, \cdot {\text{Re}} = \frac{{\rho {\text{*}}\omega {\text{*}}H{{{\text{*}}}^{2}}}}{{\mu {\text{*}}}}. \\ \end{gathered} $$

(1.2)

Here, Sh = ω*H*/U* and Re = ρ*U*H*/μ* are the Strouhal and Reynolds numbers for the channel flow. We will consider the flow regimes for which all terms in the momentum equation are of the same order, i.e., Sh ∙ Re = B ~ O(1).

On the upper and lower channel walls we specify the no-slip conditions for the velocity: u(t, y = 0) = u(t, y = 1) = 0.

In dimensionless form the pressure distribution along the channel reads:

$$p = {{p}_{0}} + A{\text{sin}}t-(A{\text{sin}}(t))x.$$

(1.3)

Here, p₀ is the dimensionless pressure in the steady-state flow in a channel section taken as the origin of the coordinate system. The solution of Eqs. (1.2) for the velocity profile can be represented as the sum of the steady-flow velocity and the pulsatory component:

$$u(t,y) = {{u}_{0}}(y) + {{u}_{1}}(t,y).$$

The velocity profile for the classic Poiseuille flow takes the form:

$${{u}_{0}}(y) = \frac{1}{2}(y - {{y}^{2}}).$$

(1.4)

From the linearity of Eq. (1.2) it follows that u₁(t, y) can be sought as the real part of the solution of an equation for a complex-valued function V(t, Y). This equation with the corresponding boundary conditions read:

$$\frac{{\partial V}}{{\partial t}} = \frac{{{{\partial }^{2}}V}}{{\partial {{Y}^{2}}}} - {{A}_{1}}i\exp (it),\quad Y = y\sqrt B ,\quad {{A}_{1}} = \frac{A}{B},\quad V(t,0) = V(t,\sqrt B ) = 0.$$

(1.5)

Here, i is the imaginary unit. The solution of (1.5) is sought in the form V(t, Y) = A₁exp(it)g(Y), then from (1.5) we obtain the following boundary-value problem for g(Y):

$$\frac{{{{d}^{2}}g}}{{d{{Y}^{2}}}} - ig - i = 0,\quad g(0) = g(\sqrt B ) = 0.$$

(1.6)

The analytical solution of ordinary differential equation (1.6) is found using a standard method. This solution can be represented in the form:

$$g(Y) = \frac{{{\text{Cosh}}(cY - c\sqrt B {\text{/}}2)}}{{{\text{Cosh}}(c\sqrt B {\text{/}}2)}} - 1,\quad c = \frac{{1 + i}}{{\sqrt 2 }}.$$

(1.7)

Here, Cosh(Z) is the hyperbolic cosine of the argument Z. Now we obtain the required pulsatory velocity component u₁(t, y) by calculating the real part of V(t, Y):

$$\begin{gathered} {{u}_{1}}(t,y) = {\text{Real}}\{ (A{\text{/}}B)g(y\sqrt B )\exp (it)\} \\ = \;\alpha \left[ {\exp ({{Y}_{1}})\cos ({{Y}_{1}} + t) + \exp \left( {{{Y}_{1}} + \sqrt {\frac{B}{2}} } \right)\cos \left( {{{Y}_{1}} - \sqrt {\frac{B}{2}} + t} \right)} \right. \\ \left. { + \;\exp \left( { - {{Y}_{1}} + \sqrt {\frac{B}{2}} } \right)\cos \left( { - {{Y}_{1}} + \sqrt {\frac{B}{2}} + t} \right) + \exp ( - {{Y}_{1}} + \sqrt {2B} )\cos (t - {{Y}_{1}})} \right] - \frac{A}{B}{\text{cos(}}t) \\ \alpha = \frac{A}{{B[1 + 2\exp (\sqrt {B{\text{/}}2} )\cos (\sqrt {B{\text{/}}2} ) + \exp (\sqrt {2B} )]}},\quad {{Y}_{1}} = y\sqrt {\frac{B}{2}} . \\ \end{gathered} $$

(1.8)

Similar solutions, but in different notation, are known in the literature. In particular, in [15] a solution was constructed for a pulsating flow in a channel with more general time dependences of the pressure gradient.

It should be noted that the pulsatory component of the longitudinal velocity depends non-monotonically on the vertical coordinate (Fig. 1). The local maxima are located at a certain distance from the walls, and this distance varies during the pressure fluctuation period.

Fig. 1.

Instantaneous profiles of the fluctuating velocity component u₁(t, y) at a succession of times; B = 100, A = 100, solid lines: t = {0, π/4, π/2, 3π/4} (1–4), broken lines: t ={π, 5π/4, 3π/2, 7π/4} (5–8).

The obtained expressions for the instantaneous pressure in the fluid p(t, x) and the velocity profile u(t, y) = u₀(y) + u₁(t, y) will be used below in specifying the boundary conditions for the flow over a small chosen rectangular cavity located on the lower channel wall, with a compressible gas bubble inside.

As is clear in Fig. 2, the fluctuations of the pressure and shear-stress on the wall occur with the same period but shifted phases. For other values of A, the qualitative behavior of the curves will not change. At large values of B, such time intervals exist on which the pressure starts to decrease (and hence the bubble in the cavity grows) but the friction still increases (and vise versa). As a rule, an increase in the pressure over the bubble results in a shift of the phase interface into the cavity and, as a result, in an increase in the average friction. Thus, according to the solution of the Navier-Stokes equations, simultaneous fluctuations of the pressure and the longitudinal velocity near the wall may result in both the co-directed and counter-directed actions on the average friction in the flow over a microcavity with a gas bubble.

Fig. 2.

Typical time dependences of the pressure (broken line) and the derivative of the velocity (dimensionless shear stress) on the wall; p₀ =1, the shear stress τ_w is scaled to τ_w0 = 1/2, corresponding to the channel flow in the absence of pressure fluctuations; A = 1, B = 100, 10, 1 (curves 1–3).

2 FLOW ON THE SCALE OF A CAVITY

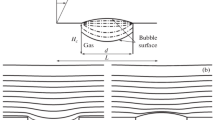
Near the channel wall, we consider an outer pulsating flow over a single rectangular microcavity containing a compressible gas bubble. This problem formulation corresponds to the modeling of unsteady flow over a chosen element of a periodic superhydrophobic surface containing rectangular microcavities which are partially or completely filled with a compressible gas (Fig. 3).

Fig. 3.

A conditional diagram of a pulsating flow in a channel over a chosen microcavity of a striped superhydrophobic wall; L is the period length, H_c is the cavity depth, d is the cavity width, δ is the initial shift of the meniscus into the cavity; broken lines show the possible locations of the bubble surface in the course of oscillations.

In Fig. 3, the geometric proportions between the dimensions of the macrochannel and the microcavties are not kept correctly. In reality, the dimensions of a single cavity are very small (do not exceed hundreds micrometers). This is why the flow on the macroscale (the scale of the channel width) plays the role of the ‘outer’ asymptotic solution, and the flow on the microcavity scale can be regarded as the ‘inner’ asymptotic solution. Accordingly, in formulating the boundary conditions on the scale of the cavity with a gas bubble we should use the near-wall asymptotics of the solution obtained in the previous section of the paper. To describe the flow near the cavity, we introduce a local Cartesian coordinate system with the origin located in the middle of the segment connecting the upper corners of the cavity.

As the local linear scale we use the period L* of the superhydrophobic-wall texture (L* ≪ H*), as the velocity scale U$_{{in}}^{*}$ we use the velocity of the outer steady flow in the absence of fluctuations at a distance L* from the wall; the scale of the spatial pressure drop near the cavity is μ*U*/L*, and the full dimensional pressure in the ‘inner’ region can be represented in the form:

$$p_{{in}}^{*} = K{\text{*}}H{\text{*}}\left( {{{p}_{0}} + A\sin t + \frac{{L{\text{*}}}}{{H{\text{*}}}}{{p}_{{in}}}(t,{{x}_{{in}}},{{y}_{{in}}})} \right).$$

(2.1)

Here, the value of the dimensionless pressure (p₀ + Asin(t)) coincides with the corresponding value obtained in the outer problem solution in the channel section over the middle of the cavity (see formula (1.3)). The subscript in here and below refers to the flow parameters in the inner flow region: (x*, y*) = (x_inL*, y_inL*), u* = uU$_{{in}}^{*}$, ${v}{\text{*}}$ = ${v}U_{{in}}^{*}$. The local flow on the scale L* with a characteristic velocity U$_{{in}}^{*}$ is characterized by small Reynolds numbers, this is why the flow near the cavity is described by the Stokes equations:

$${{\nabla }^{2}}{\mathbf{u}_{{in}}} - \nabla {{p}_{{in}}} = 0,\quad \nabla \cdot {\mathbf{u}_{{in}}} = 0.$$

(2.2)

The fluctuations of the outer flow make a double impact on the local flow near the microcavity. The first impact consists in the variation of the instantaneous velocity profile ahead of and behind the cavity. The second impact is the variation of the instantaneous pressure over the cavity (and hence the volume of the gas bubble and the location of the bubble surface), which results in the variation of the instantaneous flow domain. The problem formulation for Eqs. (2.2) is quasi-steady, since the time enters as a parameter in the specification of the phase interface position and the flow velocity on the calculation domain boundaries.

For each time instant, at the inlet and outlet of the calculation domain (ahead of and behind the cavity) we specify a plane-parallel flow with a linear velocity profile, corresponding to the linear part of solution (1.8):

$$\begin{array}{*{20}{c}} {{{u}_{{in}}}\left( {t, - 1{\text{/}}2,{{y}_{{in}}}} \right) = {{u}_{{in}}}\left( {t,1{\text{/}}2,{{y}_{{in}}}} \right) = (U{\text{*/}}U_{{in}}^{*})u\left( y \right) = {{u}_{0}}\left( y \right) + {{u}_{1}}\left( {t,y} \right),} \\ {{{y}_{{in}}} \in \left[ {0;\;1} \right] = y{{H{\text{*}}} \mathord{\left/ {\vphantom {{H{\text{*}}} {L{\text{*}}}}} \right. \kern-0em} {L{\text{*}}}}.} \end{array}$$

According to the scales chosen, on the outer edge of the calculation domain (y_in = 1) we have: u_in = u_in(t, –1/2, 1). On the solid boundaries we specify the no-slip condition u = 0. On the bubble surface, the no-flow condition u ∙ n = 0 and the absence of the shear stress are specified: τ_ijn_je_i = 0, where τ_ij are the components of the shear stress tensor, n_j are the components of the normal vector, and e_i are the basis vectors, i, j take the values 1 or 2; the repeating indexes signify summation.

At each instant of time, the pressure inside the bubble is assumed to be uniform over the space. The pressure variation along the phase interface in the cavity, attributable to the fluid motion, is much smaller than the difference of the static pressures in the fluid over the cavity and in the gas bubble [6]; this is why, as in statics, the bubble surface can be approximated by a circle arc. The dimensional radius of curvature of the bubble surface meniscus r* is determined by the angle of wetting at the points of touching the meniscus with the cavity walls. In our problem formulation this angle is assumed to be known.

In the coordinate system $x_{{in}}^{*}Oy_{{in}}^{*}$ used in this section, with the origin located in the middle of the cavity, the dimensionless equation for the bubble surface shape takes the form (below, the subscript in is omitted):

$$y = - \delta \pm \sqrt {{{r}^{2}} - {{{(d{\text{/}}2)}}^{2}}} \mp \sqrt {{{r}^{2}} - {{x}^{2}}} ,\quad x \in \left[ { - d{\text{/}}2,d{\text{/}}2} \right].$$

(2.3)

In nondimensionalization of Eq. (2.3), all quanities with dimension of length are scaled to the period length L*; r is the dimensionless radius of curvature of the bubble surface, d is the dimensionless width of the cavity with the gas bubble, and δ is the dimensionless shift of the edge points of the meniscus into the cavity. The choice of the upper or lower sign in (2.3) depends on the direction of convexity of the bubble surface: into the cavity or into the bulk flow of the fluid. We note that during one period of pressure fluctuations in the channel the direction of convexity of the bubble can change.

The instantaneous bubble volume V$_{g}^{*}$(t) is determined from the condition of constant mass of the gas in the cavity m$_{g}^{*}$, with the solvability of the gas being neglected. It is assumed that the gas is perfect, accordingly we have:

$$p_{g}^{*}\left( {t{\text{*}}} \right)V_{g}^{*}\left( {t{\text{*}}} \right) = m_{g}^{*}R{\text{*}}T_{g}^{*}.$$

(2.4)

The subscript g denotes the parameters of the gas, R* is the gas constant, and T$_{g}^{*}$ is the gas temperature assumed to be constant. The equation relating the static pressure over the bubble in the middle of the cavity p$_{e}^{*}$ and the pressure in the bubble takes the form:

$$p_{e}^{*}\left( {t{\text{*}}} \right) - p_{g}^{*} = \pm \frac{{\Sigma {\text{*}}}}{{r{\text{*}}\left( {t{\text{*}}} \right)}}.$$

(2.5)

Here, Σ* is the surface tension coefficient. The radius of curvature of the meniscus is assumed to be constant while the bubble surface travels inside the cavity and does not reach its upper corners. After reaching the upper corners of the cavity, the radius of curvature of the bubble surface is found using the condition of known bubble volume and the equation of a circle arc touching the upper corners of the cavity. The oscillating static pressure over the cavity p$_{e}^{*}$ is related with the pressure distribution in the macroproblem (1.3) by the formula:

$$p_{e}^{*}(t) = K{\text{*}}H{\text{*}}({{p}_{0}} + A\sin (t)).$$

(2.6)

Thus, for given values of the gas mass in the bubble, the gas temperature, and the angle of wetting the problem formulation for finding the shape and location of the phase interface in the cavity (2.2)–(2.6) becomes closed and matched with the outer problem of pulsating flow in the channel. It should be noted that the amplitude of pressure oscillations in the bubble can vary substantially depending on the ratio of the amplitude of pressure gradient oscillations in the channel A to the value of the local static pressure over the cavity p₀; i.e. for different cavities located along the lower channel wall this amplitude is different. This is why in discussing the calculation results we will consider several qualitatively different cases of oscillations of the bubble meniscus, which are of the main interest.

For solving Stokes equations (2.2) at a given instantaneous fluid velocity profile and a meniscus position, we use the boundary integral equation method [16]. To be more specific, we use a variant of an algorithm of this method developed earlier in [6–8]. This method has substantial advantages as compared to finite-difference methods of solving the Stokes equations, since it makes it possible to reduce the original problem by one dimension and to avoid the difficulties associated with the finite-difference approximation of infinite derivatives of the parameters near the points of matching the no-slip boundary conditions on the solid wall and zero shear stress on the bubble surface. According to the boundary integral equation method, the fluid velocity field u satisfying Eqs. (2.2) can be found by the convolution of the fundamental solutions of the Stokes operator with certain their beforehand unknown ‘densities’ distributed over the flow domain boundary:

$$\begin{gathered} \Lambda {{u}_{j}}({\mathbf{x}_{0}}) = - \frac{1}{{4\pi }}\int\limits_\Gamma {{{f}_{i}}(\mathbf{x}){{G}_{{ij}}}(\mathbf{x},{\mathbf{x}_{0}})dl(\mathbf{x})} + \frac{1}{{4\pi }}\int\limits_\Gamma {{{u}_{i}}(\mathbf{x}){{T}_{{ijk}}}(\mathbf{x},{\mathbf{x}_{0}}){{n}_{k}}(\mathbf{x})dl(\mathbf{x})} , \\ {{G}_{{ij}}} = - {{\delta }_{{ij}}}{\text{ln}}r + \frac{{{{\xi }_{i}}{{\xi }_{j}}}}{{{{r}^{2}}}},\quad {{T}_{{ijk}}} = - 4\frac{{{{\xi }_{i}}{{\xi }_{j}}{{\xi }_{k}}}}{{{{r}^{4}}}}, \\ \boldsymbol\xi = \mathbf{x} - {\mathbf{x}_{0}},\quad r = \left| \xi \right|. \\ \end{gathered} $$

(2.7)

Here, G_ij(x, x₀) and T_ijk(x, x₀) are the fundamental solutions of the two-dimensional Stokes operator called the ‘stokeslet’ and ‘stresslet’; x and x₀ are the points lying on the boundary and inside the calculation domain, respectively; Λ equals to 1/2 and 1 for the boundary and inner points of the calculation domain; Γ is the calculation domain boundary; f = σ_ijn_je_i is the stress vector; i, j, and k are equal to 1 or 2; repeating indexes mean summation.

The densities of the distributions of the fundamental solutions are found from integral boundary equations (2.7) written for the points of the calculation domain boundary. As a result of solving these equations the fluid velocity on the interface is also calculated. The numerical solution of the boundary integral equations is found using a collocation method. In doing this, the calculation domain boundary is represented in the form of a polygonal curve containing straight segments (‘elements’) and the integrals are replaced by discrete integral sums of local integrals over each element. The densities of the ‘stresslet’ and ‘stokeslet’ distributions on each element are assumed to be constant. As a result, we obtain a system of linear algebraic equations for discrete values of these densities. In writing the boundary integral equations on the elements where |x – x₀| → 0 there appear two types of singularities, namely, a logarithmic singularity and that of 1/r kind. The integrals over the elements containing the singularities are calculated analytically with the help of introducing a local coordinate system fitted to element’ center, in the same way as in [18]. The integrals over other elements are calculated using the quadrature formulas of fifth order. The obtained system of linear algebraic equations should be accomplished with the equations corresponding to the boundary conditions specified on the phase interface and on the inlet/outlet sections of the channel, which are considered as the equations written for the boundary points. The periodic boundary conditions for the points lying in the inlet/outlet sections of the calculation domain are replaced by their finite-difference analogs, which are written for each point of the inlet/outlet section of the calculation domain and added to the system of linear algebraic equations as additional equations for unknown components of the velocity vector $u$. The resulting final system of linear algebraic equations is solved by a standard Gauss method. In our calculations, the typical number of boundary elements was of the order of 10³. This ensured the sufficient accuracy of calculating all required flow parameters (up to two decimal points), which was verified by the further increase in the number of boundary elements.

In addition to [6–8], last years other authors also started to use the boundary integral equation method for numerical studies of viscous fluid flows near superhydrophobic surfaces. For example, in [17] a variant of the boundary element method was used for a biharmonic equation, the solution of which was constructed using the ‘stream function–vorticity’ variables. In [9, 18], the method of boundary integral equations was used for calculating Stokes flows over cavities filled with another viscous fluid, with different ratios of the viscosities of the outer and inner fluid.

After the calculation of the velocity field in the fluid and on the bubble surface from the solution of a system of boundary integral equations satisfying the specified boundary conditions, we calculate the instantaneous, averaged over the texture period, effective characteristics of the superhydrophobic surface: the average velocity slip of the fluid ${{u}_{w}} = \langle {{u}_{{in\,}}}_{w}\rangle$ and ${{\tau }_{w}} = {{\left. {\left\langle {{{\partial {{u}_{{in}}}} \mathord{\left/ {\vphantom {{\partial {{u}_{{in}}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right\rangle } \right|}_{w}}$, i.e. the value proportional to the average friction on the wall. For a bubble convex into the cavity, the average ‘velocity slip length’ can be calculated directly by the formula $b = {{\left\langle {{{u}_{{in\,w}}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{u}_{{in\,w}}}} \right\rangle } {\left( {{{{\left. {\left\langle {{{\partial {{u}_{{in}}}} \mathord{\left/ {\vphantom {{\partial {{u}_{{in}}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right\rangle } \right|}}_{w}}} \right)}}} \right. \kern-0em} {\left( {{{{\left. {\left\langle {{{\partial {{u}_{{in}}}} \mathord{\left/ {\vphantom {{\partial {{u}_{{in}}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right\rangle } \right|}}_{w}}} \right)}}$. Here, $\left\langle \cdot \right\rangle$ signifies the averaging over the period of the texture, containing a bubble, the subscript w corresponds to the parameters calculated on the straight line connecting the upper corners of the cavity. For a bubble whose surface protrudes from the cavity into the region of the bulk flow, we use a specific procedure proposed earlier in [8] for calculating the average values of the velocity slip and the friction. After the calculation of the instantaneous values of the parameters averaged over the texture period we can perform time averaging over the fluctuation period.

3 CALCULATION RESULTS

In [7, 8], it was shown that for a periodic system of cavities located on a superhydrophobic surface the periodic velocity profile formed between the cavities differs from the linear profile only slightly when the system of cavities is sufficiently rarefied (d*/L* < 0.5). This is why below we present the calculations of averaged parameters on the wall u_w and τ_w for d*/L* = 0.5 and 0.6. For smaller values of d*/L* the effects attributable to the flow fluctuations and the shift of the meniscus into the cavity are qualitatively similar to the results presented below.

Figure 4 shows the instantaneous streamline patterns for several instants of time, calculated for the cavity with d*/L* = 0.6, H$_{{\text{c}}}^{*}$/L* = 0.5, and the initial condition δ*/L* = 0.1; the angle θ = –20°, and the amplitude of fluctuations of the local static pressure over the bubble is ~60%. Here, θ is the angle between the horizontal and the bubble surface (see Fig. 3). These streamline patterns show the main specific features of the flow restructuring which may occur during one fluctuation period of the bubble surface, such as: the formation of one large eddy occupying the entire space in the cavity over the bubble; the formation of local eddies near the edge points of the meniscus; and a shear flow of the fluid along the phase interface when the cavity is completely occupied by the gas bubble. The bubble surface can be convex into the cavity or protrude from the cavity into the bulk flow. In deeper cavities, two large counter-rotating eddies can be formed.

Fig. 4.

Instantaneous streamline patterns over the gas bubble in the cavity with d*/L* = 0.6, H$_{{\text{c}}}^{*}$/L* = 0.5: δ*/L* = 0.2 (t = π/2), 0.1 (t = 0, π, 2π), θ = –20° (a, b); δ*/L* = 0, θ = –20° (t = 1.2π, 1.8π), the angle θ = 30° (t = 3π/2) (c, d).

The analysis of instantaneous streamline patterns obtained in the calculations indicated that the flow structure over the phase interface is determined by the gas section portion d*/L*, the cavity depth H$_{{\text{c}}}^{*}$/L*, the initial position of the meniscus in the cavity δ*/L*, and the instantaneous shape of the bubble surface depending on the amplitude of pressure fluctuations over the cavity.

In Figs. 5–8, we present the time dependences of the instantaneous values of the velocity slip u_w and friction τ_w averaged over the period L*. They are calculated for several sets of the outer flow parameters and geometric parameters of the initial flow domain, which correspond to qualitatively different modes of oscillations of the phase interface. For all calculations presented, the value of the dimensionless static pressure over the cavity p₀ was set equal unity, so the value of the parameter A determines the amplitude of the pressure oscillations.

Fig. 5.

Typical dependences of the instantaneous values of the velocity slip u_w (a) and friction τ_w (b) averaged over the spatial period: 1, pulsating flow, 2, flow with neglected fluctuations of the velocity profile, 3, mean (averaged over the pressure fluctuation period) values of the effective parameters; A = 0.13, B = 1, H$_{{\text{c}}}^{*}$/L* = 1, d*/L* = 0.5, θ = –40°.

Fig. 6.

Typical time dependences of the instantaneous values of the fluid velocity slip u_w (a) and friction τ_w (b) averaged over the spatial period: 1, pulsating flow, 2, flow with neglected fluctuations of the velocity profile, 3, mean (averaged over the pressure fluctuation period) values of the effective parameters; A = 0.46, B = 1, H$_{{\text{c}}}^{*}$/L* = 0.5, d*/L* = 0.5, δ*/L* = 0.1, θ = –10°.

Fig. 7.

Typical dependences of the instantaneous values of the fluid velocity slip u_w (a) and friction τ_w (b) averaged over the spatial period: 1, pulsating flow, 2, flow with neglected fluctuations of the velocity profile, 3, mean (averaged over the pressure fluctuation period) values of the effective parameters; A = 0.22, B = 1, H$_{{\text{c}}}^{*}$/L* = 1, d*/L* = 0.6, θ = –30°.

Fig. 8.

Typical dependences of the instantaneous values of the fluid velocity slip uw (a) and friction τw (b) averaged over the spatial period: 1, pulsating flow, 2, flow with neglected fluctuations of the velocity profile, 3, mean (averaged over the pressure fluctuation period) values of the effective parameters; A = 0.08, B = 1, H$_{{\text{c}}}^{*}$/L* = 1, d*/L* = 0.6, θ = 20°.

In the calculations shown in Fig. 5, the initial state corresponds to a curved bubble surface attached to the corner points of the cavity δ*/L* = 0; the limiting state corresponding to the minimal local pressure over the bubble is a plane phase interface connecting the upper corner points of the cavity. In the calculations the fluctuations of ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}$ on the wall in front of and ahead of the cavity attained ~15%. The calculated values of u_w and τ_w are scaled to u_w0 and τ_w0 which correspond to the same initial state of the bubble in the steady channel flow with the Poiseuille profile. The broken line shows the calculations in which we neglected the fluctuations of the velocity profile but took into account the pressure fluctuations, same as in [14]. For 0 < t < 3.14, the pressure in the cavity is greater than the initial value, the edge points of the meniscus move up relative to the vertical cavity walls but the shape of the meniscus does not change; for 3.14 < t < 6.28 the edge points of the meniscus coincide with the corner points of the cavity, the gas in the cavity expands, and the shape of the meniscus varies and tends to the limiting position. In the gas compression stage the instantaneous characteristics of the superhydrophobic surface deteriorate and in the expansion stage with the surface straightening these characteristics improve, as compared to the initial state. For other values of the geometrical parameters of the cavity and the same initial position of the bubble surface the dependences of the instantaneous values of u_w and τ_w on t qualitatively coincide with the curves presented in Fig. 5. The absence of symmetry of curves (1) with respect to the quarter of the period is attributable to the phase shift between the oscillations of the pressure over the bubble and the velocity shear near the wall. If in the calculations we take into account only the pressure fluctuations then the curve branches become symmetrical with respect to the quarter of the fluctuation period (2). For the pulsating flow, the mean, i.e., averaged over the fluctuation period, value of the effective ‘velocity slip length’ is b = u_w/τ_w ≈ 0.03, and the ratio of the ‘velocity slip lengths’ in the flows with and without fluctuations is equal to b/b₀ ≈ 1.07. Hence, for the given initial position of the meniscus, the considered amplitudes of the local pressure fluctuations over the bubble, and the velocity shear ahead of the cavity, the fluctuations imposed slightly increase the ‘velocity slip length’ (basic characteristic of the drag reduction efficiency in the flow over a superhydrophobic surface) as compared to the steady-state flow.

Figure 6 shows the dependence of the instantaneous values of u_w and τ_w calculated for another initial position of the bubble surface in the cavity. At the initial instant of the fluctuations t = 0, the edge points of the meniscus are shifted into the cavity, i.e., the bubble occupies only part of the cavity. The limiting position corresponding to the minimal value of the pressure over the bubble is a flat phase interface connecting the upper corner points of the cavity. In the calculations, the fluctuations of ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}$ on the wall ahead of and behind the cavity attained ~40%. The results obtained are scaled to u_w0 and τ_w0 calculated for the same initial position of the bubble surface in the steady-state flow. For 0 < t < 3.14, the pressure over the phase interface is greater than the initial one, the gas in the cavity is compressed additionally, and the meniscus move down relative to cavity walls, with the meniscus shape being unchanged; for 3.14 < t < 6.28, the gas expands, the edge points of the meniscus go up to the corner points of the cavity, and the bubble surface shape tends to its limiting position. When the gas is compressed, the instantaneous characteristics important for the superhydrophobic surface (e.g., the velocity slip length) deteriorate, and when the gas expands and the bubble surface is straightened the characteristics improve, as compared to the initial state of the gas in the cavity. For other geometric parameters of the cavity and the same initial position of the bubble surface, the dependences of the instantaneous parameters of the superhydrophobic surface coincide qualitatively with those shown in Fig. 6. An analysis of the results for the case considered indicates that the value of the fluid velocity slip u_w averaged over the fluctuation period is smaller than in the previous case, when in the initial state the gas bubble occupied the entire volume of the cavity and the edge points of the meniscus coincided with the corner points of the cavity. At the same time, the value of τ_w averaged over the fluctuation period is much greater than in the case when the edge points of the cavity were fixed at the upper cavity corner points for the same values of A and B. For the considered pulsating flow, the value of the effective velocity slip length averaged over the fluctuation period is b = u_w/τ_w ≈ 0.024, and the ratio of the velocity slip lengths b/b₀ ≈ 1.39. In this case, the fluctuations imposed improve significantly the property of the superhydrophobic surface to reduce the average friction in the flow of a viscous fluid.

Figure 7 shows the calculation results for the case when after the compression stage the gas starts to expand and the bubble surface starts to protrude from the cavity into the bulk flow. At the initial instant of fluctuations t = 0 the phase interface connects the upper corner points of the cavity, and in the limiting position the bubble surface protrudes from the cavity. In the calculations, the fluctuations of ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}$ on the wall ahead of and behind the cavity attained ~25%. The results are scaled to u_w0 and τ_w0 calculated for the same initial position of the bubble surface in the steady-state Poiseuille flow. For other initial values of the parameters and the pressure fluctuation amplitude, which determines the value of the bubble surface protrusion from the cavity, the calculation results coincide qualitatively with those shown in Fig. 7. For the pulsating flow, the value of the effective velocity slip length averaged over the fluctuation period is b = u_w/τ_w ≈ 0.05 and b/b₀ ≈ 1.05.

Figure 8 shows the calculation results for the situation when at the initial instant t = 0 the phase interface is fixed at the corner points of the cavity and protrudes from the cavity into the outer flow. The limiting state corresponding to the maximal local pressure over the cavity is the bubble with a flat surface. In the calculations, the fluctuations of ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}$ on the wall ahead of and behind the cavity attained ~9%. As before, the parameters averaged over L* are scaled to u_w0 and τ_w0, calculated for the same initial state of the bubble in the steady state flow without velocity fluctuations. For the pulsating flow, the value of the effective velocity slip length was b = u_w/τ_w = 0.091 and b/b₀ ≈ 1.02.

The analysis of gas bubble pulsations in the cavity, attributable to the outer flow fluctuations, indicates that over a wide range of parameters there exists a time interval when the edge points of the meniscus are shifted into the cavity. In this situation, the instantaneous properties of the superhydrophobic surface deteriorate significantly. Nevertheless, the main qualitative result obtained in the calculations consists in the fact that small harmonic fluctuations of the pressure and the flow velocity near a superhydrophobic surface with microcavities occupied by gas bubbles do not decrease (and for some initial positions of the meniscus in the cavity even noticeably increase) the effective fluid ‘velocity slip length’ on the wall, i.e. prompts the reduction of the average friction on the superhydrophobic surface.

SUMMARY

On the basis of parametric calculations of a pulsating viscous-fluid flow over a two-dimensional microcavity with a gas bubble, the estimates of variation of the average parameters of the flow over the cavity (the velocity slip, the average friction, and the ‘velocity slip length’) are obtained for different modes of imposed pressure and velocity fluctuations, and different initial positions of the bubble surface in the cavity. It is shown that, as compared to the steady-state flow, the imposed fluctuations do not decrease (under some conditions even increase) the average velocity slip and the friction reduction effect in the flow over a striped superhydrophobic surface with microcavities occupied by gas bubbles. The results obtained may explain a possible mechanism of a noticeable friction reduction in turbulent regimes of viscous-fluid flows along superhydrophobic surfaces.