Numerical Solution Methods for a Nonlinear Operator Equation Arising in an Inverse Coefficient Problem

Abstract

We consider the inverse problem of determining two unknown coefficients in a linear system of partial differential equations using additional information about one of the solution components. The problem is reduced to a nonlinear operator equation for one of the unknown coefficients. The successive approximation method and the Newton method are used to solve this operator equation numerically. Results of calculations illustrating the convergence of numerical methods for solving the inverse problem are presented.

1. INTRODUCTION

Consider the problem of determining functions $u(x,t)$ and $a(x,t)$ such that

$$ u_x+a_t=0,\quad 0\leq x\leq l,\quad 0\leq t\leq T, $$

(1.1)

$$ a_t=\gamma (t)(\varphi (t)u-a),\quad 0\leq x\leq l,\quad 0\leq t\leq T,$$

(1.2)

$$ u(0,t)=\mu (t),\quad 0\leq t\leq T, $$

(1.3)

$$ a(x,0)=\psi (x),\quad 0\leq x\leq l. $$

(1.4)

This problem is a mathematical model of the sorption dynamic process [1, p. 174; 2, p. 6] under the assumption that the absorbent properties change over time.

The existence and uniqueness of the solution of the following inverse problem were studied in [3].

Assume that the functions $\mu (t)$ and $\psi (x)$ are given and the functions $\gamma (t)$ and $\varphi (t)$ are unknown. It is required to determine $\gamma (t)$, $\varphi (t)$, $u(x,t)$, and $a(x,t)$ from the following additional information about one of the components of the solution to problem (1.1)–(1.4):

$$ u(l,t)=g(t),\quad 0\leq t\leq T, $$

(1.5)

$$ u_x(l,t)=p(t),\quad 0\leq t\leq T. $$

(1.6)

We will assume that the given functions $\mu (t)$, $\psi (x)$, $g(t)$, and $p(t)$ satisfy the following conditions.

Conditions A.

One has $\mu ,g,p\in C[0,T]$; $\psi \in C[0,l]$; $\mu (t)>0$, $g(t)>0$, and $p(t)<0$ for $0\leq t\leq T$; $\psi (x)\ge 0$ for $0\leq x\leq l$; $\psi (l)=0$; and $\psi (x)$ is not zero identically.

Let us give the definition of solution of the inverse problem. Let $t_0\in (0,T]$. We introduce the rectangle $Q_{t_0}=\{(x,t):0\leq x\leq l$, $0\leq t\leq t_0\}$.

Definition.

A quadruple of functions $(\gamma (t),\varphi (t), u(x,t),a(x,t))$ is called a solution of the inverse problem for $t\in [0,t_0]$ if $\gamma ,\varphi \in C[0,t_0]$, $u,u_x,a,a_t\in C(Q_{t_0})$, $\gamma (t)>0$ and $\varphi (t)>0$ for $0\leq t\leq t_0$, $u(x,t)>0$ and $a(x,t)\ge 0$ for $(x,t)\in Q_{t_0}$, and $\gamma (t)$, $\varphi (t)$, $u(x,t)$, and $a(x,t)$ satisfy Eqs. (1.1) and (1.2) and conditions (1.3)–(1.6) in $Q_{t_0}$.

Here are some results in [3] to be used in what follows.

Given a function $\gamma (t)$, consider the integral equation

$$ \eqalign { u(x,t)&=\mu (t)\exp \big \{\!-R(t;\gamma )x\big \}+ \gamma (t)\exp \left \{\!-\!\int _0^t\gamma (\theta )\,d\theta \right \} \int _0^x\exp \big \{\!-R(t;\gamma )(x-s)\big \}\psi (s)\,ds \cr &\quad {}+\gamma (t)\int _0^x\int _0^t \exp \left \{-R(t;\gamma )(x-s)-\int _{\tau }^t\gamma (\theta )\,d\theta \right \} R(\tau ;\gamma )u(s,\tau ) \,d\tau \,ds,\; (x,t)\in Q_{t_0},}$$

(1.7)

for the function $u(x,t)$, where

$$ R(t;\gamma )=-\left [p(t)+\gamma (t)\int _0^tp(\tau ) \,d\tau \right ]\big (g(t)\big )^{-1}.$$

Under Conditions A, there exists a unique solution of the integral equation (1.7). To emphasize the dependence of this solution on the function $\gamma (t)$, we denote it by $u(x,t;\gamma )$.

Let us define the operator

$$ \eqalign { (A\gamma )(t)&=\left [g(t)-\mu (t)\exp \big \{-R(t;\gamma )l\big \}- \gamma (t)\int _0^l\int _0^t H(l,s,t,\tau ;\gamma )R(\tau ;\gamma )u(s,\tau ;\gamma )\,d\tau \,ds\right ] \cr &\qquad {}\times \left (\,\int _0^lH(l,s,t,0;\gamma )\psi (s)\,ds\right )^{-1},\quad 0\leq t\leq t_0,} $$

(1.8)

where

$$ H(x,s,t,\tau ;\gamma )= \exp \left \{-R(t;\gamma )(x-s)-\int _{\tau }^t \gamma (\theta )\,d\theta \right \}. $$

It was shown in [3] that solving the inverse problem is reduced to solving the nonlinear operator equation

$$ \gamma (t)=(A\gamma )(t),\quad 0\leq t\leq t_0. $$

(1.9)

The present paper deals with numerical methods for solving Eq. (1.9) and the above-stated inverse problem. We use two iterative methods, the successive approximation method and the Newton method, to solve the nonlinear operator equation (1.9). There are quite a few papers dealing with iterative methods for solving operator equations to which inverse problems can be reduced (see, e.g., [4,5,6,7,8,9,10,11]). Many of them are determined by the peculiarities and specific features of each specific inverse problem.

Consider the successive approximation method for the operator equation (1.9).

Assume that the inequality

$$ g(0)-\mu (0)\exp \big \{(p(0)/g(0))l\big \}>0 $$

(1.10)

is satisfied. Define the positive constant

$$ \gamma _0=\bigg (g(0)-\mu (0)\exp \Big \{\big (p(0)/g(0)\big )l\Big \}\bigg ) \left (\,\int _0^l\exp \Big \{\big (p(0)/g(0)\big )(l-s)\Big \}\psi (s) \,ds\right )^{-1}. $$

Let us introduce the set of functions

$$ \Gamma _0=\big \{\gamma (t):\gamma \in C[0,t_0],\; \gamma _0/2\leq \gamma (t)\leq 3\gamma _0/2,\; 0\leq t\leq t_0\big \}.$$

Consider the sequence of functions $\gamma _n(t)$, $n=0,1,2,\ldots$, recursively defined by the successive approximation method for solving Eq. (1.9),

$$ \gamma _0(t)\in \Gamma _0,\quad \gamma _{n+1}(t)=(A\gamma _n)(t),\quad n=0,1,2,\ldots$$

(1.11)

The results in [3] imply an assertion about the convergence of the successive approximation method.

Theorem 1.

Let the functions $\mu (t)$, $\psi (x)$, $g(t)$, and $p(t)$ satisfy conditions A and inequality (1.10). Then there exists a $t_0\in (0,T]$ such that, for each function $\gamma _0(t)\in \Gamma _0$, the sequence of functions $\gamma _n(t)$ belongs to the set $\Gamma _0$ and uniformly converges as $n\to \infty$ to a continuous function $\bar {\gamma }(t)$ that is a solution of Eq. (1.9).

2. NEWTON METHOD

Consider the application of the Newton method to the numerical solution of the inverse problem under study. As was already noted, it suffices to apply the Newton method to solve the nonlinear operator equation (1.9).

To construct the Newton method, one needs to know the derivative of the operator defined by formula (1.8). First, let us study the differentiability of the solution of the integral equation (1.7) with respect to the parameter.

Consider functions $\gamma (t)$ and $\gamma _{\Delta }(t)$ and a number $\varepsilon$ such that the functions $\gamma (t)$ and $\gamma (t)+\xi \gamma _{\Delta }(t)$ are positive and continuous on the interval $[0,t_0]$ for all $\xi \in (-\varepsilon ,\varepsilon )$.

Lemma.

If conditions A are satisfied, then the solution $u(x,t;\gamma +\xi \gamma _{\Delta })$ of Eq. (1.7) has the partial derivative $\dfrac {\partial u}{\partial \xi }(x,t;\gamma +\xi \gamma _{\Delta })\Big |_{\xi =0}$.

Proof. Consider the function

$$ v(x,t;\gamma ,\gamma _{\Delta },\xi ) =\frac {u(x,t;\gamma +\xi \gamma _{\Delta })- u(x,t;\gamma )}{\xi }. $$

Since the functions $u(x,t;\gamma +\xi \gamma _{\Delta })$ and $u(x,t;\gamma )$ are solutions of Eq. (1.7) for $\gamma (t)+\xi \gamma _{\Delta }(t)$ and $\gamma (t)$, respectively, it follows that $v(x,t;\gamma ,\gamma _{\Delta },\xi )$ satisfies the equation

$$ \eqalign { v(x,t;\gamma ,\gamma _{\Delta },\xi )&=\frac {F_1(x,t;\gamma ,\gamma _{\Delta },\xi ) -F_1(x,t;\gamma ,0,0)}{\xi } \cr &\quad {}+\int _0^x\int _0^t\frac {F_2(x,t,s,\tau ;\gamma ,\gamma _{\Delta },\xi ) -F_2(x,t,s,\tau ;\gamma ,0,0)}{\xi }u(s,\tau ;\gamma +\xi \gamma _{\Delta })\,d\tau \,ds \cr &\quad {}+\int _0^x\int _0^tF_2(x,t,s,\tau ;\gamma ,0,0) v(s,\tau ;\gamma ,\gamma _{\Delta },\xi )\,d\tau \,ds,\enspace (x,t)\in Q_{t_0}, \enspace (x,t)\in Q_{t_0}, }$$

(2.1)

where

$$ F_1(x,t;\gamma ,\gamma _{\Delta },\xi ) =\mu (t)\exp \big \{-R(t;\gamma +\xi \gamma _{\Delta })x\big \}+ \big (\gamma (t)+\xi \gamma _{\Delta }(t)\big )\int _0^x H(x,s,t,0;\gamma +\xi \gamma _{\Delta })\psi (s) \,ds$$

and $F_2(x,t,s,\tau ;\gamma ,\gamma _{\Delta },\xi )= (\gamma (t)+\xi \gamma _{\Delta }(t)) H(x,s,t,\tau ;\gamma + \xi \gamma _{\Delta })R(\tau ;\gamma +\xi \gamma _{\Delta }).$ Passing to the limit as $\xi \to 0$, we obtain

$$ \lim \limits _{\xi \to 0}\big [F_1(x,t;\gamma ,\gamma _{\Delta },\xi )- F_1(x,t;\gamma ,0,0)\big ]/\xi =F_3(x,t;\gamma ,\gamma _{\Delta }),$$

(2.2)

$$ \lim \limits _{\xi \to 0}\big [F_2(x,t,s,\tau ;\gamma ,\gamma _{\Delta },\xi )- F_2(x,t,s,\tau ;\gamma ,0,0)\big ]/\xi =F_4(x,t,s,\tau ;\gamma ,\gamma _{\Delta }),\qquad$$

(2.3)

where

$$ \eqalign { F_3(x,t;\gamma ,\gamma _{\Delta })&=\mu (t)\exp \big \{-R(t;\gamma )x\big \}\frac {1}{g(t)} \int _0^tp(\theta )\,d\theta x\gamma _{\Delta }(t)+ \gamma _{\Delta }(t)\int _0^x H(x,s,t,0;\gamma )\psi (s) \,ds \cr &\quad {}+\gamma (t)\int _0^x H(x,s,t,0;\gamma )\left (\frac {1}{g(t)} \int _0^tp(\theta )\,d\theta (x-s)\gamma _{\Delta }(t)- \int _0^t\gamma _{\Delta }(\theta )\,d\theta \right )\psi (s)\,ds } $$

and

$$ \eqalign { F_4(x,t,s,\tau ;\gamma ,\gamma _{\Delta })&=\gamma _{\Delta }(t) H(x,s,t,\tau ;\gamma )R(\tau ;\gamma ) \cr &\quad {}+\gamma (t)H(x,s,t,\tau ;\gamma )\left (\frac {1}{g(t)} \int _0^tp(\theta )\,d\theta (x-s)\gamma _{\Delta }(t)- \int _{\tau }^t\gamma _{\Delta }(\theta )\,d\theta \right ) R(\tau ;\gamma ) \cr &\quad {}-\gamma (t)H(x,s,t,\tau ;\gamma )\frac {1}{g(\tau )} \int _0^{\tau }p(\theta )\,d\theta \gamma _{\Delta }(\tau ). }$$

Equation (2.1) is a Volterra integral equation of the second kind for the function $v(x,t;\gamma ,\gamma _{\Delta },\xi )$. Solving it for $v(x,t;\gamma ,\gamma _{\Delta },\xi )$, passing to the limit as $\xi \to 0$, and using formulas (2.2) and (2.3), we find that the derivative ${\partial u(x,t;\gamma +\xi \gamma _{\Delta })}/\partial \xi$ exists for $\xi =0$. Denote it by $w(x,t;\gamma ,\gamma _{\Delta })$. Equation (2.1) implies that $w(x,t;\gamma ,\gamma _{\Delta })$ is a solution of the integral equation

$$ \eqalign { w(x,t;\gamma ,\gamma _{\Delta })&=F_3(x,t;\gamma ,\gamma _{\Delta })+ \int _0^x\int _0^tF_4(x,t,s,\tau ;\gamma ,\gamma _{\Delta })u(s,\tau ;\gamma )\,d\tau \,ds \cr &\quad {}+\int _0^x\int _0^tF_2(x,t,s,\tau ;\gamma ,0,0)w(s,\tau ;\gamma ,\gamma _{\Delta })\,d\tau \,ds, \quad (x,t)\in Q_{t_0}. }$$

(2.4)

The proof of the lemma is complete.

Let us study the Gateaux differentiability of the operator $A$ defined in (1.8). It follows from the results in [3] that there exists a $t_0\in (0,T]$ such that $A$ maps the set $\Gamma _0$ into itself. In what follows, we assume that the number $t_0$ satisfies this condition.

We introduce the set

$$ \Gamma _{{00}}=\big \{\gamma (t):\gamma \in C[0,t_0],\ \ \gamma _0/2<\gamma (t)<3\gamma _0/2,\ \ 0\leq t\leq t_0\big \}. $$

Theorem 2.

If conditions A and inequality (1.10) are satisfied, then, for each function $\gamma \in \Gamma _{00}$, the operator $A$ is Gateaux differentiable on $\Gamma _{00}$.

Proof. Let $\gamma (t)$ be an arbitrary function in $\Gamma _{00}$, and let $\gamma _{\Delta }(t)$ be a function and $\xi$ a number such that the function $\gamma (t)+\xi \gamma _{\Delta }(t)$ belongs to the set $\Gamma _{00}$ as well. Let us show that the functions $((A(\gamma +\xi \gamma _{\Delta }))(t)-(A\gamma )(t))/\xi$ converge uniformly on the interval $[0,t_0]$ as $\xi \to 0$.

Consider the functions

$$ \frac {1}{\xi }\left [\left (\,\int _0^lH(l,s,t,0;\gamma +\xi \gamma _{\Delta })\psi (s)\,ds\right )^{-1} -\left (\,\int _0^lH(l,s,t,0;\gamma )\psi (s)\,ds\right )^{-1} \right ]. $$

They uniformly converge on the interval $[0,t_0]$ to the function

$$ \eqalign { F_5(t;\gamma ,\gamma _{\Delta })&= -\left (\,\int _0^lH(l,s,t,0;\gamma )\psi (s)\,ds\right )^{-2} \cr &\quad {}\times \int _0^lH(l,s,t,0;\gamma ) \left [\frac {1}{g(t)}\int _0^tp(\theta )\,d\theta (l-s)\gamma _{\Delta }(t)- \int _0^t\gamma _{\Delta }(\theta )\,d\theta \right ]\psi (s) \,ds }$$

(2.5)

as $\xi \to 0$.

It follows from the lemma that the functions

$$ \gamma (t)\int _0^l\int _0^t H(l,s,t,\tau ;\gamma )R(\tau ;\gamma ) \frac {u(s,\tau ;\gamma +\xi \gamma _{\Delta }) -u(s,\tau ;\gamma )}{\xi }\,d\tau \,ds $$

uniformly converge on the interval $[0,t_0]$ to the function

$$ \gamma (t)\int _0^l\int _0^t H(l,s,t,\tau ;\gamma )R(\tau ;\gamma )w(s,\tau ;\gamma ,\gamma _{\Delta })\,d\tau \,ds $$

(2.6)

as $\xi \to 0$. It follows from formulas (2.3), (2.5), and (2.6) that

$$ \eqalign { \lim \limits _{\xi \to 0}&\frac {(A(\gamma +\xi \gamma _{\Delta }))(t)-(A\gamma )(t)}{\xi }= \left (\,\int _0^lH(l,s,t,0;\gamma )\psi (s)\,ds\right )^{-1} \cr &\quad {}\times \left [-\frac {\mu (t)}{g(t)}\int _0^tp(\theta )\,d\theta \exp \big \{\!-R(t;\gamma )l\big \}l\gamma _{\Delta }(t) -\int _0^l\int _0^t F_4(l,t,s,\tau ;\gamma ,\gamma _{\Delta })u(s,\tau ;\gamma )\,d\tau \,ds\right ] \cr &\quad {}-\left (\gamma (t)\int _0^l\int _0^t H(l,s,t,\tau ;\gamma )R(\tau ;\gamma )w(s,\tau ;\gamma ,\gamma _{\Delta })\,d\tau \,ds\right )\! \left (\,\int _0^lH(l,s,t,0;\gamma )\psi (s)\,ds\right )^{-1} \cr &\quad {}+\left [g(t)-\mu (t)\exp \big \{\!-R(t;\gamma )l\big \}-\gamma (t)\int _0^l\int _0^t H(l,s,t,\tau ;\gamma )R(\tau ;\gamma )u(s,\tau ;\gamma )\,d\tau \,ds\right ] \cr &\qquad \qquad \times F_5(t;\gamma ,\gamma _{\Delta }), }$$

(2.7)

where the function $w(x,t;\gamma ,\gamma _{\Delta })$ is determined from Eq. (2.4). Thus, the operator $A$ is Gateaux differentiable on the set $\Gamma _{00}$, and its derivative $A^{\prime}[\gamma ]\gamma _{\Delta }$ is determined by the right-hand side of Eq. (2.7). The proof of the theorem is complete.

The iterative process corresponding to the Newton method [12, p. 669] is defined as follows. One specifies the function $\gamma _0(t)$. The subsequent functions $\gamma _{n+1}(t)$, $n=0,1,\ldots$, are determined by the formula $\gamma _{n+1}(t)=\gamma _n(t)+\gamma _{\Delta n}(t)$, where $\gamma _{\Delta n}(t)$ is the solution of the linear integral equation

$$ \gamma _{\Delta n}-A^{\prime}[\gamma _n]\gamma _{\Delta n}=-\gamma _n+A\gamma _n.$$

(2.8)

3. NUMERICAL EXPERIMENTS

Let us present the results of some numerical experiments in which the successive approximation method (1.11) and the Newton method (2.8) were used to solve the inverse problem under study.

The general scheme of computational experiments was as follows. The functions $\mu (t)$, $\gamma (t)$, and $\varphi (t)$ were specified on the interval $[0,T]$, and the function $\psi (x)$ was defined on the interval $[0,l]$. With these functions, problem (1.1)–(1.4) was solved, and the functions $g(t)=u(l,t)$ and $p(t)=u_x(l,t)$ were determined. Then the operator equation (1.9) with the functions $\mu (t)$, $g(t)$, $p(t)$, and $\psi (x)$ was solved by the iterative methods (1.11) and (2.8), and the approximate function $\tilde {\gamma }(t)$ was found. To determine the approximate function $\tilde {\varphi }(t)$, we used the formula [3]

$$ \tilde {\varphi }(t)=-\left [p(t)+\tilde {\gamma }(t)\int _0^tp(\tau )\,d\tau \right ] (g(t)\tilde {\gamma }(t))^{-1}. $$

(3.1)

One and the same initial approximation $\gamma _0(t)=\gamma _0$ and the same stopping criterion

$$ \big \|\gamma _{n+1}(t)-\gamma _{n}(t)\big \|_{C[0,T]} \Big (\big \|\gamma _{n}(t)\big \|_{C[0,T]}\Big )^{-1}\leq \delta$$

were used in the approximate solution of the operator equation (1.9) by both iterative methods.

In the first computational experiment, $T=0.5$, $l=1$, and

$$ \mu (t)=1+t,\quad \psi (x)=2-2x,\quad \gamma (t)=3+\sin (2\pi t),\quad \varphi (t)=0.5+0.1\cos (2\pi t).$$

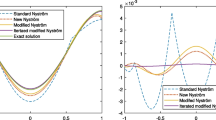
Figure 1 shows the function $\gamma (t)=3+\sin (2\pi t)$, the first iteration $\gamma ^{I}_{1}(t)$ and the second iteration $\gamma ^{I}_{2}(t)$ of the successive approximation method, and the first iteration $\gamma ^{N}_{1}(t)$ and the second iteration $\gamma ^{N}_{2}(t)$ of the Newton method. For $\delta =0.001$, the successive approximation method stopped at the 9th iteration step, and the Newton method stopped at the 6th iteration step. In the scale of Fig. 1, the approximate solutions $\tilde {\gamma }^{I}(t)=\gamma ^{I}_{9}(t)$ and $\tilde {\gamma }^{N}(t)=\gamma ^{N}_{6}(t)$ thus obtained visually coincide with the exact solution $\gamma (t)=3+\sin (2\pi t)$ and hence are not shown.

Figure 2 shows the function $\varphi (t)=0.5+0.1\cos (2\pi t)$ and the functions $\varphi ^{I}_{1}(t)$, $\varphi ^{I}_{2}(t)$, $\varphi ^{N}_{1}(t)$, and $\varphi ^{N}_{2}(t)$ obtained by the substitution of the functions $\gamma ^{I}_{1}(t)$, $\gamma ^{I}_{2}(t)$, $\gamma ^{N}_{1}(t)$, and $\gamma ^{N}_{2}(t)$, respectively, into formula (3.1). The approximate solutions $\tilde {\varphi }^{I}(t)=\varphi ^{I}_{9}(t)$ and $\tilde {\varphi }^{N}(t)=\varphi ^{N}_{6}(t)$ obtained in a similar manner visually coincide with the exact solution $\varphi (t)=0.5+0.1\cos (2\pi t)$ and hence are not shown.

Fig. 1.

Results of the first computational experiment: the exact function $\gamma (t)$ and the functions defined on the first two iterations.

Fig. 2.

Results of the first computational experiment: the exact function $\varphi (t)$ and the functions defined on the first two iterations.

In the second computational experiment, $T=0.5$, $l=1$, and

$$ \mu (t)=1+t,\quad \psi (x)=2-2x,\quad \gamma (t)=1.5-0.5\sin (\pi t),\quad \varphi (t)=2+0.5\sin (2\pi t). $$

The parameter $\delta$ was chosen to be $0.001$. By analogy with Fig. 1, Fig. 3 shows the values of the exact function $\gamma (t)$ as well as the functions obtained on the first two iterations for both methods. The convergence criterion was satisfied at the 7th step of the successive approximation method and at the 9th step of the Newton method. The approximate solutions $\tilde {\gamma }^{I}(t)=\gamma ^{I}_{7}(t)$ and $\tilde {\gamma }^{N}(t)=\gamma ^{N}_{9}(t)$ found at the final iteration of both methods visually match the exact solution in the scale of Fig. 3.

Figure 4 shows the function $\varphi (t)=2+0.5\sin (2\pi t)$ as well as the functions $\varphi ^{I}_{1}(t)$, $\varphi ^{I}_{2}(t)$, $\varphi ^{N}_{1}(t)$, and $\varphi ^{N}_{2}(t)$ corresponding to the first two iterations. The functions $\tilde {\varphi }^{I}(t)=\varphi ^{I}_{7}(t)$ and $\tilde {\varphi }^{N}(t)=\varphi ^{N}_{9}(t)$ found by formula (3.1) coincide in the figure with $\varphi (t)=2+0.5\sin (2\pi t)$.

Fig. 3.

Results of the second computational experiment: the exact function $\gamma (t)$ and the functions defined on the first two iterations.

Fig. 4.

Results of the second computational experiment: the exact function $\varphi (t)$ and the functions defined on the first two iterations.

The above examples, as well as a number of other numerical calculations, allow us to conclude that the convergence of both methods is quite fast and that there are no significant advantages in the rate of convergence of one of the methods in comparison with the other.