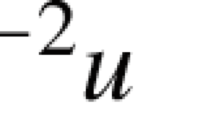Skip to main content
SpringerLink
Log in

Spectral Properties of the Cauchy Problem for a Second-Order Operator with Involution

  • ORDINARY DIFFERENTIAL EQUATIONS
  • Published:
Differential Equations Aims and scope Submit manuscript

Abstract

We study the spectral properties of the Cauchy problem for the differential operator \(-u^{{\prime \prime }}(x)+\alpha u^{{\prime \prime }}(-x) \) with an involution for \(\alpha \) satisfying the inequalities \(0<|\alpha |<1 \). Based on the analysis of the spectrum and the Green’s function constructed here, it is shown that if the parameter \(\varkappa =\sqrt {(1-\alpha )/(1+\alpha )}\) is irrational, then the system of root functions is complete but is not a basis in \(L_2\). In the opposite case, it is established that the root functions can be chosen to form an unconditional basis in \(L_2 \).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Note that zero does not belong to the spectrum of the operator \(\mathcal {L}_\alpha \).

  2. Here and throughout the following, by \(C,C_1,\ldots \) we denote some positive constants.

  3. The symbol \(\|\cdot \|_2 \) from now on denotes the norm on \(L_2(-1,1) \).

  4. The Green’s function \( G(x,t;\lambda )\) is constructed just as in [14]. The particular form of the Green’s function in (19) was provided to the present authors by A.M. Sarsenbi.

REFERENCES

  1. Przeworska-Rolewicz, D., Equations with Transformed Argument. Algebraic Approach, Amsterdam–Warszawa: Elsevier-PWN, 1973.

    MATH  Google Scholar 

  2. Wiener, J., Generalized Solutions of Functional Differential Equations, Singapore–New Jersey–London–Hong Kong: World Scientific, 1993.

    Book  Google Scholar 

  3. Wu, J., Theory and Applications of Partial Functional Differential Equations, New York: Springer, 1996.

    Book  Google Scholar 

  4. Cabada, A. and Tojo, F.A.F., Differential Equations with Involutions, Amsterdam–Paris–Beijing: Atlantis, 2015.

    Book  Google Scholar 

  5. Kurdyumov, V.P. and Khromov, A.P., Riesz bases formed by root functions of a functional-differential equation with a reflection operator, Differ. Equations, 2008, vol. 44, no. 2, pp. 196–204.

    Article  MathSciNet  Google Scholar 

  6. Burlutskaya, M.Sh. and Khromov, A.P., On one theorem on equiconvergence on the entire interval for functional-differential operators, Izv. Saratov. Univ. Ser. Mat. Mekh. Inf., 2009, vol. 9, no. 4(1), pp. 3–10.

    Article  Google Scholar 

  7. Burlutskaya, M.Sh. and Khromov, A.P., Fourier method in an initial-boundary value problem for a first-order partial differential equation with involution, Comput. Math. Math. Phys., 2011, vol. 51, no. 12, pp. 2102–2114.

    Article  MathSciNet  Google Scholar 

  8. Burlutskaya, M.Sh., Asymptotic formulas for eigenvalues and eigenfunctions of a functional-differential operator with involution, Vestn. Voronezh. Gos. Univ. Cer. Fiz. Mat., 2011, no. 2, pp. 64–72.

  9. Burlutskaya, M.Sh., Mixed problem for a first-order partial differential equation with involution and periodic boundary conditions, Comput. Math. Math. Phys., 2014, vol. 54, no. 1, pp. 1–10.

    Article  MathSciNet  Google Scholar 

  10. Kurdyumov, V.P., On Riesz bases of eigenfunctions of a second order differential operator with involution and integral boundary conditions, Izv. Saratov. Univ. Ser. Mat. Mekh. Inf., 2015, vol. 15, no. 4, pp. 392–405.

    Article  Google Scholar 

  11. Sadybekov, M.A. and Sarsenbi, A.M., Criterion for the basis property of the eigenfunction system of a multiple differentiation operator with an involution, Differ. Equations, 2012, vol. 48, no. 8, pp. 1112–1118.

    Article  MathSciNet  Google Scholar 

  12. Kopzhassarova, A.A. and Sarsenbi, A.M., Basis properties of eigenfunctions of second-order differential operators with involution, Abstr. Appl. Anal., 2012, article ID 576843.

  13. Kritskov, L.V. and Sarsenbi, A.M., Riesz basis property of system of root functions of second-order differential operator with involution, Differ. Equations, 2017, vol. 53, no. 1, pp. 33–46.

    Article  MathSciNet  Google Scholar 

  14. Kritskov, L.V. and Sarsenbi, A.M., Equiconvergence property for spectral expansions related to perturbations of the operator \(-u^{{\prime \prime }}(-x) \) with initial data, Filomat, 2018, vol. 32, no. 3, pp. 1069–1078.

    Article  MathSciNet  Google Scholar 

  15. Shkalikov, A.A. and Vladykina, V.E., Spectral properties of ordinary differential operators with involution, Dokl. Ross. Akad. Nauk, 2019, vol. 484, no. 1, pp. 12–17.

    MATH  Google Scholar 

  16. Kal’menov, T.Sh. and Iskakova, U.A., A criterion of strong solvability of a mixed Cauchy problem for the Laplace equation, Dokl. Ross. Akad. Nauk, 2007, vol. 414, no. 2, pp. 168–171.

    MathSciNet  MATH  Google Scholar 

  17. Figueroa, R. and Pouso, R.L., Minimal and maximal solutions to second-order boundary value problems with state-dependent deviating arguments, Bull. London Math. Soc., 2011, vol. 43, pp. 164–174.

    Article  MathSciNet  Google Scholar 

  18. Kirane, M. and Nasser, A.-S., Inverse problems for a nonlocal wave equation with an involution perturbation, J. Nonlinear Sci. Appl., 2016, vol. 9, pp. 1243–1251.

    Article  MathSciNet  Google Scholar 

  19. Ashyralyev, A. and Sarsenbi, A.M., Well-posedness of a parabolic equation with involution, Numer. Funct. Anal. Optim., 2017, vol. 38, no. 10, pp. 1295–1304.

    Article  MathSciNet  Google Scholar 

  20. Sarsenbi, A.A., Ill-posed problem for heat equation with involution, Zh. Srednevolzhsk. Mat. O-va, 2019, vol. 21, no. 1, pp. 48–59.

    MathSciNet  Google Scholar 

  21. Kritskov, L.V. and Sarsenbi, A.M., Spectral properties of a nonlocal problem for a second-order differential equation with an involution, Differ. Equations, 2015, vol. 51, no. 8, pp. 984–990.

    Article  MathSciNet  Google Scholar 

  22. Kritskov, L.V. and Sarsenbi, A.M., Basicity in \(L_p \) of root functions for differential equations with involution, Electron. J. Differ. Equat., 2015, vol. 2015, no. 278, pp. 1–9.

    MathSciNet  MATH  Google Scholar 

  23. Il’in, V.A., On connection between the form of boundary conditions and the properties of basicity and equiconvergence with a trigonometric series of expansions in the root functions of a nonself-adjoint differential operator, Differ. Uravn., 1994, vol. 30, no. 9, pp. 1516–1529.

    Google Scholar 

  24. Kritskov, L.V., Sadybekov, M.A., and Sarsenbi, A.M., Nonlocal spectral problem for a second-order differential operator with an involution, Bull. Karaganda Univ. Math., 2018, vol. 91, no. 3, pp. 53–60.

    Article  Google Scholar 

  25. Kritskov, L.V., Sadybekov, M.A., and Sarsenbi, A.M., Properties in \(L_p \) of root functions for a nonlocal problem with involution, Turk. J. Math., 2019, vol. 43, pp. 393–401.

    Article  MathSciNet  Google Scholar 

  26. Khinchin, A.Ya., Tsepnye drobi (Continued Fractions), Moscow: Nauka, 1978.

    Google Scholar 

  27. Naimark, M.A., On some tests for the completeness of the system of eigenvectors and associated vectors of a linear operator in a Hilbert space, Dokl. Akad. Nauk SSSR, 1954, vol. 98, no. 5, pp. 727–730.

    MathSciNet  Google Scholar 

Download references

Funding

The work by L.V. Kritskov was supported by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan, project no. AP 08855792.

Author information

Authors and Affiliations

  1. Lomonosov Moscow State University, Moscow, 119991, Russia

    L. V. Kritskov & V. L. Ioffe

Authors
  1. L. V. Kritskov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. L. Ioffe
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to L. V. Kritskov or V. L. Ioffe.

Additional information

Translated by V. Potapchouck

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kritskov, L.V., Ioffe, V.L. Spectral Properties of the Cauchy Problem for a Second-Order Operator with Involution. Diff Equat 57, 1–10 (2021). https://doi.org/10.1134/S0012266121010018

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0012266121010018

Search

Navigation