Skip to main content
SpringerLink
Log in

On Libration Points in the Asteroid–Research Probe System

  • Published:
Cosmic Research Aims and scope Submit manuscript

Abstract

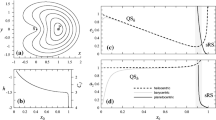
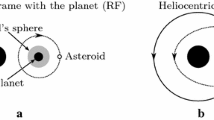
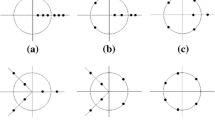
This paper is dedicated to a study of relative motion in the field of homogeneous spheroid bodies. It is assumed that an asteroid’s satellite does not affect its translational and rotational motion by inertia. The latter motion has the form of rotation in the mode of regular precession. The case in which the asteroid is an ellipsoid of revolution is considered. A system of conditions that the libration points must satisfy is constructed; it is shown that its solution is two types of libration points, which differ in their location with respect to the constant vector of the angular momentum and the axis of symmetry of the ellipsoid. Thereafter, the stability of libration points is investigated numerically and analytically in the first approximation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.

Similar content being viewed by others

REFERENCES

  1. Markeev, A.P., Tochki libratsii v nebesnoy mekhanike i kosmodinamike (Libration Points in Celestial Mechanics and Cosmodynamics), Moscow: Nauka, 1978.

  2. Batrakov, Yu.V., Periodic motions of a particle in the gravitational field of a rotating triaxial ellipsoid, Byull. Inst. Teor. Astron., 1957, vol. 6, no. 8, pp. 524–542.

    MathSciNet  Google Scholar 

  3. Abalakin, V.K., On the question of the stability of a libration point in the vicinity of a rotating gravitating ellipsoid, Byull. Inst. Teor. Astron., 1957, vol. 6, no. 8, pp. 543–549.

    Google Scholar 

  4. Beletsky, V.V., Generalized restricted circular three-body problem as a model for dynamics of binary asteroids, Cosmic Res., 2007, vol. 45, no. 5, pp. 408–416.

    Article  ADS  Google Scholar 

  5. Beletsky, V.V. and Rodnikov, A.V., Coplanar libration points in the generalized restricted circular problem of three bodies, Nelin. Din., 2011, vol. 7, no. 3, pp. 569–576.

    Google Scholar 

  6. Beletsky, V.V. and Rodnikov, A.V., Libration points of the generalized restricted circular problem of three bodies in the case of imaginary distance between attracting centers, Nelin. Din., 2012, vol. 8, no. 5, pp. 931–940.

    Google Scholar 

  7. Rodnikov, A.V., Triangular libration points of the generalized restricted circular problem of three bodies for conjugate complex masses of attracting centers, Nelin. Din., 2014, vol. 10, no. 2, pp. 213–222.

    MATH  Google Scholar 

  8. Rodnikov, A.V., On a particle motion along the leier fixed in a precessing rigid body, Nelin. Din., 2011, vol. 7, no. 2, pp. 295–311.

    Google Scholar 

  9. Appell, P., Traité de mécanique rationnelle, Paris: Gauthier-Villar, 1941, vol. 2.

    MATH  Google Scholar 

  10. Duboshin, G.N., Nebesnaya mekhanika. Osnovnye zadachi i metody (Celestial Mechanics. Main Problems and Methods), Moscow: Nauka, 1968.

Download references

Author information

Authors and Affiliations

  1. Institute of Mechanics, Moscow State University, 119991, Moscow, Russia

    E. K. Lavrovsky

Authors
  1. E. K. Lavrovsky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. K. Lavrovsky.

Additional information

Translated by M. Chubarova

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lavrovsky, E.K. On Libration Points in the Asteroid–Research Probe System. Cosmic Res 61, 305–313 (2023). https://doi.org/10.1134/S0010952523700211

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0010952523700211

Search

Navigation