Abstract
The interaction of the magnetospheric–ionospheric (MI) system surrounding the Earth with the environment (solar wind) occurs in the form of a series of transient processes at different scales. The largest of them, magnetic storms, are obviously triggered by disturbances in the solar wind (direct driving). The role of the internal dynamics of the MI system, which is caused to a large extent by the nonlinearity and temporal delays of the loading–unloading processes of energy and particle from the solar wind into the magnetosphere, becomes more significant at smaller scales (substorms, pseudobreakups, injections, and activations). A typical dynamic state of the MI system is characterized as self-organized criticality or turbulence, which are characterized by statistical scale invariance (scaling) in the fluctuation distributions of many characteristics. The dynamics of the MI system is projected into the region of the auroral oval, the very existence of which is due to this dynamics. The space–time structure of auroral disturbances largely reflects the structure of processes in the MI plasma. The description of this structure is important both for studying the fundamental study of plasma processes and for many topical applied problems related to the propagation of radio waves in the ionosphere and vital activity at high latitudes. The paper discusses approaches and developments for constructing a model of the space–time structure of the auroral oval, based on fractal and multifractal characteristics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
INTRODUCTION
The magnetospheric–ionospheric (MI) system surrounding the Earth is an open nonlinear distributed dynamic system in a complex structured environment, the solar wind. Simple electrodynamic considerations (a cavity with plasma created by the field of a permanent magnet, which is flowed around by a stream of charged particles with a frozen magnetic field) give a representation of the global structure of the MI system. From general physical considerations, due to the limited volume of the MI system and its spatial distribution, interaction with the external environment during long-term evolution brings the system to a state in which it balances on the threshold of stability, and it is convenient for the system to dump excess energy/particles. Constant interaction with an inhomogeneous medium manifests itself, among other things, in the form of a series of transient processes at different scales, which largely determines the dynamics and the very structure of the MI system. The largest of them, magnetic storms, are apparently triggered by disturbances in the solar wind (direct driving), variations in the dynamic pressure of the solar wind and the orientation of the interplanetary magnetic field (IMF). Part of the solar-wind energy entering the MI system can be accumulated inside in the form of energization of plasma flows and current sheets. Therefore, the internal dynamics of the MI system also plays a role, which is caused to a large extent by the nonlinearity and temporal delays in the loading–unloading processes of energy and particle from the solar wind into the magnetosphere, which becomes more significant on smaller scales (substorms, pseudobreakups, injection, activation) [1]. Various plasma instabilities cause local transient processes that lead to the precipitation of energetic particles into the atmosphere, to auroral phenomena projected due to the configuration of the Earth’s magnetic field into a region called the “auroral oval” (see review [2]). Thus, the very existence of the auroral oval is determined by the plasma dynamics in the MI systems, in this case, the space–time structure of auroral disturbances, reflects the structure of processes in MI plasma [3]. The description of this structure is important both for the fundamental study of plasma processes and for many topical applied issues related to the propagation of radio waves in the ionosphere and vital activity at high latitudes [4]. Existing models describe the boundaries of the auroral oval, at best, with some division into types of precipitating particle fluxes depending on the disturbance level. However, within these boundaries, there is a significant inhomogeneity of precipitating particle fluxes in space and time, which plays an important role, for example, in the formation of the structure of MI currents [5], and not only leads to local fluctuations in the ionospheric electron concentration.
The paper discusses approaches and developments for constructing a model of the space–time structure of auroral disturbances in the auroral oval, based on fractal and multifractal characteristics, which should fill a significant gap in environmental models.
METHODOLOGICAL CONSIDERATIONS
As already mentioned, the magnetospheric–ionospheric system of the Earth is an open nonlinear distributed dynamic system, which is far from the state of thermodynamic equilibrium with the environment, the solar wind. However, under the influence of the energy/particle flux in it, the so-called “nonequilibrium study state” (NESS) arises from the solar wind [6], which is maintained by dissipation in numerous plasma instabilities and local transients (transient dissipative processes) [7]. To study this state, two approaches (languages) have historically emerged: one is based on the concept of turbulence in the broad sense [8], and the other is based on the concept of self-organized criticality (SOC) [9, 10]. Both concepts, especially their mathematical description, are an idealization that can be applied to natural objects with certain restrictions.
Both approaches are based on the property of statistical self-similarity (scaling) that often occurs in the analysis of time series, which manifests itself in the power-law distribution of values measured in natural systems [11]. Such distribution means that there is some order in seemingly random fluctuations, which can be used for inclusion in empirical models. Next, we present some regularities that can be used for this.
We note that it is precisely the attempts of a geometric description of natural structures and their complexity that led to the creation of fractal geometry [12]. The concept of self-similarity underlying this approach implies that the elements of a structure at different scales are statistically similar to each other. An expansion in scale-dependent test functions yields a power-law spectrum. In the simplest version, the structure is described by the value of the observed quantity I(x) at certain points {xi} of space Rn, and the test function is the increment dI(x, s) = I(x + s) – I(x) on spatial scale s. Statistical averaging of the value of dI(x, s)q over all points x gives a statistical moment of order q, S(s, q) = 〈dI(x, s)q〉. It should be noted that studies of high-order moments are limited by the length of the available data series and, for moments q > 6, they usually do not make sense. The power-law dependence of the statistical moments on scale s for small s, S(s, q) ~ sζ(q) indicates a fractal structure. With a linear dependence of the exponent on the moment number, ζ(q) = Hq, one speaks of a monofractal, and with a nonlinear one, of a multifractal (Fig. 1). As far as possible, it is better to use wavelet leaders having a number of advantages as trial functions [13]. To characterize the (multi)fractal structure, one can use the expansion of the ζ(q) dependence in a Taylor series at q → 0: ζ(q) = Σp≥1 cpqp/p!. In this case, the values of the first two coefficients have a simple interpretation: с1 = H > 0 and с2 = 0 in the case of a monofractal, and deviation of с2 from 0 characterizes the degree of multifractality. An example of processing the multifractal series of values for 2000 of the value (vsw Bz), the product of the solar-wind velocity and the z component of the IMF, is shown in Fig. 1. Structure function S(s, q) was constructed for scales of 4–128 min, and the bootstrap procedure was used to estimate the confidence intervals of the approximations.
STATISTICAL RESULTS FOR CHARACTERISTICS OF AURORAL TRANSIENTS
Let us consider the auroral atmospheric airglow at night as a reflection of the transient processes occurring in the MI system, regardless of the details of the physical mechanisms in MI plasma that lead to this glow. On the images of an aurora obtained by the all-sky camera (or a camera on the satellite), we select the connected areas (spots) of the glow that exceed a certain background value. Having a sufficiently long record of auroras, we will trace its history for each such spot, fixing its properties: size, integrated brightness on the frame, and lifetime. It was shown that the statistical distribution of the characteristics of the auroral glow regions in a wide range of scales has scaling properties characteristic of the SOC state [14–17] (see the example in Fig. 2).
Distribution density of the characteristics of individual auroral spots during the active phases of substorms: (a) lifetime; (b) lifetime-integrated spot area. Black symbols are from [16] according to Polar satellite data (squares) and ground-based data for January 19, 2001 (triangles). Lines are approximations by a power dependence: black for January 19, 2001; green for January 14, 2005; and red for January 28, 2001.
It was also shown that the obtained power exponents of the statistical distributions are related to each other by relations characteristic of critical phenomena [18]. Thus, these characteristics as the size and lifetime of the auroral spot are not completely independent random variables, but are consistent in a certain way. This internal matching was used, for example, in [19] to optimize the spatial and temporal resolution of the auroral camera, when designing a research satellite.
The statistical features of the spatial distribution of the auroral glow during substorm activity can also be studied using the characteristics that are usually applied to turbulent currents. According to television observations of the all sky at the Barentsburg Observatory (Spitsbergen), in [20, 21], the features of the probability-density function (PDF) of auroral fluctuations were studied at different spatial scales (Fig. 3). Observable PDFs usually have a non-Gaussian shape with heavy tails. We also analyzed the generalized structure function (GSF) of fluctuations of the auroral glow to determine the scaling properties of moments up to the sixth order and determined the evolution of the scaling indices during the substorm expansion phase. The obtained scaling features can be interpreted as signs of the turbulent motion of the magnetospheric–ionospheric plasma.
Typical distributions of the glow intensity during the recording of the auroras on January 19, 2001: (a) the number of pixels vs. the intensity for 20-s intervals, color indicates the beginning of the interval; (b) intensity fluctuations vs. scale, for an interval of 20 s, beginning from 22:26:20 UTC. Data from [21].
Using newer data from the ALIS system cameras, the scaling in auroras was analyzed in [22] using logarithmic diagrams constructed using the discrete wavelet transform of the data [23], as well as the functions of the standard deviation, excess, and fluctuation-probability density. It was shown that the images of substorm auroral forms are close to self-similarity. Aurora fluctuations in different emission lines exhibit very similar scale behavior. A comparison was made with the electric field fluctuations observed by the Dynamics Explorer 2 satellite under substorm conditions. It was shown that the signs of intermittency in turbulent characteristics are more pronounced for substorm electric fields than for auroral fluctuations.
RESULTS: CHARACTERISTICS OF INDIVIDUAL TRANSIENTS
Not only in statistics, but also within an individual auroral transient, there are various similarities between space–time scales.
Estimates of the dimension of isolines of equal intensity in images containing auroras carried out by the simplest method of box dimension were given in [24, 25]. The spectra of the dimension of the isolines, the dependences of the dimension on the level, for which the isoline was built, were obtained. These spectra make it possible to localize the auroral form from the background glow, identify the range of glow intensities associated with the most developed structures in the auroral form, and trace the development of the structure of the auroral glow region. It was shown that there usually exists a level the isoline dimension of which can numerically characterize the spatial structure of the aurora on a single frame. The dimensions of isolines for diffuse shapes turn out to be larger than for more clearly localized arcs, which is intuitively clear.
In [26], the evolution of the scaling index characterizing fluctuations of the auroral glow at the beginning of the substorm explosive phase was studied. The images of the ultraviolet imager (UVI) from the Polar satellite show that this index usually varies from values less than unity to 1.5, increasing as the auroral breakup develops (Fig. 4). Similar scaling features have previously been noted for fluctuations on smaller scales from television observations of the all sky. If this behavior is interpreted in terms of nonlinear interactions between scales, then this means that the power of small-scale fluctuations is transferred over time to larger scales, a kind of reverse turbulent cascade. The scaling behavior in auroras during substorm activity was compared with the scaling behavior of a system of field-aligned current filaments simulated numerically using the model of nonlinear interactions of Alfvén coherent structures according to the scenario of [27]. This scenario also assumes a reverse cascade, which manifests itself in the combination of small-scale filaments of field-aligned currents of the same polarity and the formation of coarse-grained structures of field-aligned currents.
UVI images from the Polar satellite (a) before and (b) during the aurora activation on February 7, 2000, the calculation area is marked with a rectangle; (c) evolution of the scaling index. Data from [26].
A similar behavior is observed not only during substorm disturbances. In [28], a similar behavior of the scaling index is observed, in which the perturbation of the transpolar arc is activated in the northward direction of the IMF. Thus, scaling is present in the structure of the auroral glow. In this case, it seems that it underlies the processes that lead to auroral transients, regardless of their morphological classification.
To numerically estimate the degree of complexity (the number of degrees of freedom) of the processes, the approach from study [29] and the Grassberger–Procacci algorithm [30] to data of optical observations [31–33] were used in a number of studies. Estimates were obtained for the cases of pulsating auroras, substorm intensifications, and variations in the number of degrees of freedom during the development of an auroral disturbance.
RESULTS AND DISCUSSION
Some questions regarding signs of self-similarity and models leading to such manifestations require additional discussions.
On triggering in the SOC system. Strictly speaking, self-organization into a critical state under the action of a nonspecific (not explicitly imposing a structure) infinitely slow external influence, which is declared in the SOC concept, is not fulfilled for the terrestrial MI system. The solar wind also has a complex structure (see Fig. 1), and its effect on the terrestrial MI system cannot be considered weak. Nevertheless, in this case, the main conditions for the emergence of a state close to the SOC can be considered: (1) the system is limited, (2) the existence of energy (mass) flux from the external environment into the system, (3) the possibility of energy (mass) accumulation in the system with a nonlinear reset–redistribution threshold within the system, and (4) the inflow and outflow from the system are separated by space–time scales. Under such conditions, the system tends to a state in which all reservoirs in the internal phase space are close to the overflow threshold.
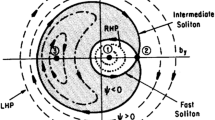
In a state close to critical, transient processes are possible that are directly triggered by disturbances in the external environment. There are many studies in the literature devoted to the comparison of triggered and spontaneous substorm disturbances of the magnetosphere depending on the features in the solar wind (usually, the most effective is considered to be a turn from the south to the north direction of the IMF, or variations in the dynamic pressure of the solar wind) (Fig. 5).
Depending on the internal state of the MI system, proximity to the threshold of the occurrence of a transient process, this triggering pulse can be more or less pronounced. In [34], for 13 substorm disturbances, angle χ between the magnetic-field vector and the solar-magnetospheric equator in the near tail of the nighttime magnetosphere was used as a characteristic of the energy accumulated in the magnetosphere according to GEOS-2 satellite data. Events were selected for Kp ≥ 4, when the satellite entered the region near the outer boundary of energetic particles. The smaller angle χ, the more stretched the magnetic field (it deviates from the dipole one) and the more energy is accumulated in the current system of the magnetotail. Smooth stretching at the preliminary phase of a substorm allows substorms to be ordered for comparison (see the diagram shown in Fig. 6). With the beginning of the substorm active phase, the magnetic field returns to a more dipole state (dipolization). For different events, the beginning of dipolization occurs at different angles. The disturbances observed in the IMF near the beginning of dipolization according to the IMP-8 (Interplanetary Monitoring Platform) and ISEE-3 (Interplanetary Sun-Earth Explorer) satellite data are shown in Fig. 6 at the bottom. For a weakly elongated magnetic field configuration, the external disturbance was stronger before the substorm. Under the conditions of a highly tail-elongated configuration, a substorm can develop spontaneously with insignificant external disturbances.
Schematic comparison of the state of the magnetosphere and the external disturbance dBz near the times of the beginning of the substorm (according to data from [34]).
Evolution of multifractal characteristics of transients. Signs of intermittency in the study of fluctuations in the magnetospheric plasma were noted by many authors according to various data. Fluctuations of the auroral glow also showed such features [20, 22]. In the general case, this means that fluctuations have not just a fractal, but a multifractal structure. In [2], a comparison of the dynamics of transient processes in four different models of two-dimensional distributed systems is performed: the cellular automaton of the Zang model (sand-pile model), damped turbulence in a liquid, the MHD model (magnetogasdynamic) of current filaments interacting due to Ampère forces (Fig. 7), and a dusty plasma crystallization model. The spatial distribution of two-dimensional fields was studied using the multifractal formalism described in Methodological Considerations. It is shown that the evolution of spatial structures arising from a random initial state has common regularities, despite the significant difference between the connections acting in the simulated systems: (1) self-similarity index с1 grows and reaches saturation and (2) the multifractality parameter с2 decreases, moving away from 0 with the development of the transient process (the width of the multifractal spectrum increases), and then returns to zero (see Fig. 7).
Processing of the results of MHD simulation of a system of current filaments interacting due to Ampère forces: (a) current distribution at the beginning (20 s) and near the maximum of transient development (60 s); (b, c) evolution of the first two cumulants (expansion according to formula (1)), characterizing the dynamics of the multifractal structure.
That is, it is multifractality that is characteristic of transients in distributed systems, and proximity to monofractality is typical of the decay phase of transients.
Anisotropy of fractal indices. It should be noted that, in many cases, the structure of the auroral glow has a clear anisotropy. Figure 8 at the top shows an example of an image of a multiple (multiplet) auroral arc observed on February 4, 2014, in Apatity (Murmansk oblast). The images were recorded by a camera with a diagonal field of view of 67° (camera 4 in the green channel, see Table 1 in [35]). For this structure, dimension df can be estimated from linear sections from the relation df – 1 = (α – 2)/2. Here, α is the scaling index obtained from logarithmic diagrams constructed using discrete wavelet decomposition [23], and corrections for distortions discussed in [36] are taken into account. Figure 8 shows a graph over the image representing the angular dependence of scaling index α. The index value is expressed as a radial distance, and the angle indicates the direction of the linear cross section of the image used to calculate the index. Dashed circles mark the extreme values of the scaling factor. The direction perpendicular to the arcs corresponds to the north–south direction. The development of the structure in dynamics can be seen in Fig. 9 at the top, which shows an auroral keogram constructed from meridional sections of camera images in the interval 18:00–18:09 UTC (Coordinated Universal Time). Figure 9 at the bottom shows the time evolution of scaling index α in the direction perpendicular and parallel to the direction of the arcs. As can be seen, in this case, the main dynamics is observed in the perpendicular structure. As is shown in [5, 37], the fractal structure of auroral precipitations is probably associated with the maintenance of the flow (percolation) of the ionospheric–magnetosphere current system.
CONCLUSIONS
From the above, the following conclusions can be drawn.
(1) The auroral oval reflects the dynamics of the magnetospheric–ionospheric system controlled by both the external environment and internal processes.
(2) Existing models do not describe the internal structure of auroral fluxes of charged auroral particles.
(3) Along with regular structures (arcs, pulsating spots), self-similarity (power-law distributions) is present in the structure of auroral precipitation in both statistical distributions and in individual transient processes.
(4) The description of these structures can be included in the model using representations of fractal geometry.
At the same time, the following features of auroral structures should be kept in mind.
(1) Anisotropy of aurora and, consequently, their fractal characteristics.
(2) In the general case, the multifractality of nonequilibrium transients, which include the observed processes in the magnetospheric–ionospheric system.
Change history
16 September 2023
An Erratum to this paper has been published: https://doi.org/10.1134/S001095252333002X
REFERENCES
Akasofu, S.-I., Polar and Magnetospheric Substorm, Dordrecht: D. Reidel, 1968. https://doi.org/10.1007/978-94-010-3461-6
Kozelov, B.V., The nature of auroras and approaches to describing the structure of the auroral glow, Mat. issled. v estestv. naukakh: Tr. 7-i Vserossiiskoi nauch. shkoly (Mathematical Research in the Natural Sciences: Proceedings of the 7th All-Russian Scientific School), October 3–6, 2011, Voitekhovskii, Yu.L., Ed., Apatity: Izd. K&M, 2011, pp. 32–47.
Yahnin, A.G., Despirak, I.V., Lubchich, A.A., et al., Relationship between substorm auroras and processes in the near-Earth magnetotail, Space Sci. Rev., 2006, vol. 122, pp. 97–106.
Sakharov, Ya.A., Mingalev, I.V., Kozelov, B.V., et al., Effect of a geomagnetic disturbance on the zone of availability of single-jump communication in the high-frequency band, Bull. Russ. Acad. Sci.: Phys., 2022, vol. 86, no. 3, pp. 310–315.
Chernyshov, A.A., Kozelov, B.V., and Mogilevsky, M.M., Study of auroral ionosphere using percolation theory and fractal geometry, J. Atmos. Sol.-Terr. Phys., 2017, vol. 161, pp. 127–133.
Milovanov, A.V., Zelenyi, L.M., and Zimbardo, G., Fractal structures and power law spectra in the distant Earth’s magnetotail, J. Geophys. Res., 1996, vol. 101, no. A9, pp. 19903–19910.
Carreras, B.A., Newman, D., Lynch V.E., and Daimond P.H., A model realization of self-organized criticality for plasma confinement, Phys. Plasmas, 1996, vol. 3, p. 2903.
Frisch, U., Turbulence: The Legacy of A.N. Kolmogorov, Cambridge: Cambridge Univ. Press, 1995.
Bak, P., How Nature Works. The Science of Self-Organized Criticality, Oxford: Oxford Univ. Press, 1997.
Jensen, H.J., Self-Organized Criticality, Cambridge: Cambridge Univ. Press, 1998.
Lui, A.T.Y., Multiscale phenomena in the near-earth magnetosphere, J. Atm. Sol.-Terr. Phys., 2002, vol. 64, pp. 125–143.
Mandelbrot, B., The Fractal Geometry of Nature, San-Francisco: Freeman, 1982.
Wendt, H., Roux, S.G., Jaffard, S., and Abry, P., Wavelet leaders and bootstrap for multifractal analysis of images, Signal Process., 2009, vol. 89, pp. 1100–1114.
Uritsky, V., Pudovkin, M.I., and Steen, A., Geomagnetic substorm as perturbed self-organized critical dynamics of the magnetosphere, J. Atm. Sol.-Terr. Phys., 2001, vol. 63, pp. 1415–1424.
Uritsky, V.M., Klimas, A.J., Vassiliadis, D., et al., Scale-free statistics of spatiotemporal auroral emissions as depicted by POLAR UVI images: Dynamic magnetosphere is an avalanching system, J. Geophys. Res., 2002, vol. 107, no. A12, p. 1426. https://doi.org/10.1029/2001000281
Kozelov, B.V., Uritsky, V.M., and Klimas, A.J., Power law probability distributions of multiscale auroral dynamics from ground-based TV observations, Geophys. Res. Lett., 2004, vol. 31, p. L20804.
Kozelov, B.V. and Roldugin, A.V., Spatial and temporal self-similarity on small scales in substorm activations, according to data from a high-speed camera in Lovozero, Bull. Russ. Acad. Sci.: Phys., 2022, vol. 86, no. 3, pp. 262–265.
Uritsky, V., Klimas, A., and Vassiliadis, D., Evaluation of spreading critical exponents from the spatiotemporal evolution of emission regions in the nighttime aurora, Geophys. Res. Lett., 2003, vol. 30, no. 15. https://doi.org/10.1029/2002GL016556
Uritsky, V.M., Donovan, E., Trondsen, T., et al., Data-derived spatiotemporal resolution constraints for global auroral imagers, J. Geophys. Res., 2010, vol. 115, p. A09205.
Kozelov, B.V. and Rypdal, K., Intermittence in auroral fluctuations during substorm, Phys. Auroral Phenomena, Proc. Proc. 29th Annual Seminar, Apatity, 2006, pp. 48–51.
Kozelov, B.V. and Rypdal, K., Spatial scaling of optical fluctuations during substorm-time aurora, Ann. Geophys., 2007, vol. 25, pp. 915–927.
Golovchanskaya, I.V., Kozelov, B.V., Sergienko, T.I., et al., Scaling behavior of auroral luminosity fluctuations observed by Auroral Large Imaging System (ALIS), J. Geophys. Res., 2008, vol. 113, p. A10303.
Abry, P., Flandrin, P., Taqqu, M.S., and Veitch, D., Wavelets for the analysis, estimation and synthesis of scaling data, in Self-Similar Network Traffic and Performance Evaluation, Park, K. and Willinger, W., Hoboken, NJ: Wiley-Interscience, 2000, pp. 39–88.
Kozelov, B.V., Fractal characteristics of the spatial structure of auroras, in Fizika okolozemnogo kosmich. prostranstva (Physics of Near-Earth Space), Apatity: Kol’sk. Nauchn. Tsentr Ross. Akad. Nauk, 2000, pp. 572–597.
Kozelov, B.V., Fractal approach to description of the auroral structure, Ann. Geophys., 2003, vol. 21, pp. 2011–2023.
Kozelov, B.V., Golovchanskaya, I.V., and Mingalev, O.V., Inverse cascade in the structure of substorm aurora and non-linear dynamics of field-aligned current filaments, Ann. Geophys., 2011, vol. 29, pp. 1349–1354.
Chang, T., Tam, S.W.Y., and Wu, C., Complexity induced anisotropic bimodal intermittent turbulence in space plasmas, Phys. Plasmas, 2004, vol. 11, no. 4, pp. 1287–1299.
Kozelov, B.V. and Golovchanskaya, I.V., Scaling of electric field fluctuations associated with the aurora during northward IMF, Geophys. Res. Lett., 2006, vol. 33, p. L20109.
Takens, F., On the numerical determination of the dimension of an attractor, in Dynamical Systems and Bifurcations, Braaksma, B.L.J., Broer, H.W., Takens, F., Groningen. Lecture Notes in Mathematics, Berlin: Springer-Verlag, 1985, vol. 1125, pp. 99–106.
Grassberger, P. and Procaccia, I., Characterization of strange attractors, Phys. Rev. Lett., 1983, vol. 50, no. 5, pp. 346–349.
Kozelov, B.V. and Vjalkova, N.Y., Search of temporal chaos in TV images of aurora, Int. J. Geomagn. Aeron., 2005, vol. 5, p. GI3005. https://doi.org/10.1029/2005GI000102
Kozelov, B.V., Kozelova, T.V., and Kornilova, T.A., Dynamics of auroral intensification as an output of magnetosphere-ionosphere system, Proc. 6th Int. Conf. Substorms, Univ. Washington, Seattle, March 25–29, 2002, pp. 432–437.
Kozelov, B.V. and Roldugin, A.V., Obtaining information on ionospheric–magnetospheric plasma from auroral observations, Bull. Russ. Acad. Sci.: Phys., 2021, vol. 85, no. 3, pp. 256–261.
Kozelova, T.V., Pudovkin, M.I., and Lazutin, L.L., Peculiarities of development of stimulated and spontaneous magnetospheric substorms according to satellite and ground data, Geomagn. Aeron., 1989, vol. 29, no. 6, pp. 910–915.
Kozelov, B.V., Pilgaev, S.V., Borovkov, L.P., and Yurov, V.E., Multi-scale auroral observations in Apatity: Winter 2010–2011, Geosci. Instrum. Method. Data Syst., 2012, vol. 1, no. 1, pp. 1–6. https://doi.org/10.5194/gi-1-1-2012
Kozelov, B.V. and Golovchanskaya, I.V., Derivation of aurora scaling parameters from ground-based imaging observations: numerical tests, J. Geophys. Res., 2010, vol. 115, p. A02204.
Chernyshov, A.A., Mogilevsky, M.M., and Kozelov, B.V., Use of fractal approach to investigate ionospheric conductivity in the auroral zone, J. Geophys. Res., 2013, vol. 118, no. 7, pp. 4108–4118.
ACKNOWLEDGMENTS
The author thanks A.V. Milovanov, I.V. Golovchanskaya, K. Rypdal, V.M. Uritsky, and A.A. Chernyshev for discussing the issues raised in this study when writing joint publications.
Funding
This study was supported by the Russian Science Foundation, grant no. 22-12-20017 “Space–Time Structures in the Near-Earth Space of the Arctic: from Aurora through the Features of Plasma Self-Organization to the Propagation of Radio Waves.”
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by N. Topchiev
The original online version of this article was revised: Due to a retrospective Open Access order.
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kozelov, B.V. Space–Time Structures in the Auroral Oval: Approaches to Modeling. Cosmic Res 61, 185–193 (2023). https://doi.org/10.1134/S001095252370020X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S001095252370020X