Stability Analysis of the PI3K–Akt–mTOR Signaling Pathway

Abstract—MAPK and PI3K−Akt−mTOR signaling cascades regulate important cellular processes. There was developed the mathematical model that was used for the analysis of the interactions within these cascades. Stability analysis of the PI3K–Ak–mTOR signaling pathway model showed that the baseline state of the signaling pathway is metastable and signal transduction can be activated by overcritical exogenous stimulation. An explicit expression was obtained for the threshold level of external stimuli. It was shown that triggering events in the dynamics of the signaling pathway are described by the fold catastrophe of the elementary catastrophe theory. A discussion about whether the results obtained are significant for molecular hematology and hemostaseology is presented.

SUPPLEMENT

I. No external stimulation. An analysis of the system of equations (1)–(3) shows that in the absence of a signal from outside (S ≡ 0), the system has two stationary states. One of them has the form

$$Y_{1}^{0} = 0,$$

(S1)

$$Y_{2}^{0} = 0,$$

(S2)

$$Y_{3}^{0} = 0,$$

(S3)

an the second has the form

$$Y_{1}^{0} = 0,$$

$$Y_{1}^{0} = \frac{{{{k}_{{32}}}{{K}_{{\text{M}}}}}}{{{{\varkappa }_{2}}}}\left[ {\frac{{{{\varkappa }_{2}}{{\varkappa }_{3}}}}{{{{k}_{2}}{{k}_{3}}}} - 1} \right],$$

(S5)

$$Y_{3}^{0} = {{K}_{{\text{M}}}}\left[ {\frac{{{{\varkappa }_{2}}{{\varkappa }_{3}}}}{{{{k}_{2}}{{k}_{3}}}} - 1} \right].$$

(S6)

It is easy to see that the second solution belongs to the region $Y_{1}^{0}$ ≥ 0, $Y_{2}^{0}$ ≥ 0, $Y_{3}^{0}$ ≥ 0 only if the condition is fulfilled

$$\mu \equiv \frac{{{{\varkappa }_{2}}{{\varkappa }_{3}}}}{{{{k}_{2}}{{k}_{3}}}} \geqslant 1.$$

(S7)

Then, in the absence of an external stimulus, the considered signal system can formally be in one of two stationary states: either in state (S1)–(S3) or in state (S4)–(S6). In order to answer in which state the system can actually be, it is necessary to analyze both stationary states for stability.

Direct research on the first ”method” of A.M. Lyapunov [19] showed that when condition (S7) is satisfied it allows us to find that the stationary state (S1)–(S3) is asymptotically stable with respect to small deviations: all three Lyapunov exponents are negative. Thus, the solution (S1)–(S3) is a node in the phase space of the considered system of equations (1)–(3). A similar study of the stationary solution (S4)–(S6) shows that, of the three Lyapunov exponents, one is positive and the other two are negative. This means that this solution is a saddle in the phase space, i.e., it is unstable to arbitrarily small disturbances and therefore cannot be physically realized.

In addition, it follows from the analysis of the foregoing that, in the complete absence of external stimulation (case S ≡ 0), the dynamics of the signaling path under consideration is actually determined by a pair of equations for Y₂ and Y₃:

$${{\dot {Y}}_{2}} = - {{\varkappa }_{2}}{{Y}_{2}} + {{k}_{{32}}}{{Y}_{3}},$$

(S8)

$${{\dot {Y}}_{3}} = {{k}_{2}}{{Y}_{2}} - {{\frac{{{{\varkappa }_{3}}{{Y}_{3}}}}{{(1 + {{{{Y}_{3}}} \mathord{\left/ {\vphantom {{{{Y}_{3}}} {{{K}_{{\text{M}}}}}}} \right. \kern-0em} {{{K}_{{\text{M}}}}}})}}}_{3}}.$$

(S9)

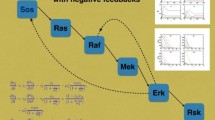
II. Stimulating mTOR with ERK. As can be seen from Fig. 1, the ERK protein is able to directly activate mTOR. This effect can be formally taken into account by adding an additional term to the equation (12). Then, system (10)–(12) takes the following form:

$${{\dot {y}}_{1}} = \Omega - {{y}_{1}}({{\varkappa }_{1}} + {{k}_{{31}}}{{K}_{{\text{M}}}}{{y}_{3}}),$$

(S10)

$${{y}_{2}} = {{y}_{1}} - {{\varkappa }_{2}}{{y}_{2}} + {{k}_{2}}{{k}_{{32}}}{{y}_{3}},$$

(S11)

$${{y}_{3}} = \Lambda + {{y}_{2}} - \frac{{{{\varkappa }_{3}}{{y}_{3}}}}{{1 + {{y}_{3}}}},$$

(S12)

where Λ is value proportional to ERK protein concentration. Given the Λ term, when searching for a stationary state, one of the nullclines will shift down by Λ:

$${{y}_{2}} = \frac{{{{\varkappa }_{3}}{{y}_{3}}}}{{1 + {{y}_{3}}}} - \Lambda .$$

(S13)

The expression for σ takes the following form:

$$\begin{gathered} \sigma = \frac{{{{y}_{3}}(\varepsilon + {{y}_{3}})(\delta - {{y}_{3}})}}{{1 + {{y}_{3}}}} - \frac{{{{\varkappa }_{2}}}}{{{{k}_{2}}{{k}_{{32}}}}}\Lambda (\varepsilon + {{y}_{3}}) \\ = \frac{{{{y}_{3}}(\varepsilon + {{y}_{3}})(\delta - {{y}_{3}})}}{{1 + {{y}_{3}}}} - \lambda (\varepsilon + {{y}_{3}}), \\ \end{gathered} $$

(S14)

where the dimensionless parameter is introduced

$$\lambda = \frac{{{{\varkappa }_{2}}}}{{{{k}_{2}}{{k}_{{32}}}}}\Lambda .$$

(S15)

The solvability condition takes the following form:

$$\begin{gathered} \sigma (1 + y_{3}^{0}) = y_{3}^{0}(\varepsilon + y_{3}^{0})(\delta - y_{3}^{0}) \\ - \,\,\lambda (\varepsilon + y_{3}^{0})(1 + y_{3}^{0}). \\ \end{gathered} $$

(S16)

Then, the expression for the value of threshold stimulation taking the λ term into account takes the form:

$${{\sigma }^{\lambda }} = \mathop {\max }\limits_{0 < x < \delta } \left[ {\frac{{x(x + \varepsilon )(\delta - x)}}{{1 + x}} - \lambda (\varepsilon + x)} \right].$$

(S17)

A comparison of expressions (21) and (S17) shows that in the presence of the λ term (λ > 0) the amplitude of the critical level of stimulation σ^λ is less than σ^#. The higher the λ value is, the lower the value of σ^λ is. Therefore, the MAPK cascade is capable of parametric destabilization of the PI3K–Akt–mTOR signaling pathway.