1. INTRODUCTION

The first papers on finding a line of bounded curvature and minimum length joining two given points are due to A.A. Markov. In [1], he discussed four problems of laying railroad tracks. The first problem was stated as the search for a line connecting two points on the plane and having the minimum length and bounded curvature, with the direction of exit of this line fixed at the first point. The corresponding shortest path is called a geodesic line. Without loss of generality, we can consider the minimum radius of curvature of such a line to be unity.

The first Markov problem can be restated as the problem of minimizing the time in which an object with limited maneuverability moving at a velocity of constant magnitude reaches the terminal point. In this setting, the problem was considered by Isaacs [2] to illustrate the example of a universal surface in the problem of a homicidal chauffeur and a stationary pedestrian. Using the Pontryagin maximum principle, Berdyshev [3] obtained a complete closed-form solution of this problem in the case where the considered object of limited maneuverability is a point. In addition, the paper [3] gives a solution of the problem on the fastest travel from a given initial state to a circle with velocity vector normal to the circle at the final time, provided that the initial object position is sufficiently far from the circle center. The result by Berdyshev supplements Markov’s results with closed-form expressions for the optimal control. The first Markov problem was solved in some more general cases: when a moving object has the shape of a circle or a segment [4, 5]; when additional control of the derivative of the velocity modulus is introduced [6, 7]; and when the moving object is subject to a constant disturbance [8].

Dubins [9] classified optimal motion trajectories in the problem of finding a line of smallest length and bounded curvature for a given direction of exit from the starting point and a given direction of arrival at the terminal point. A detailed analytical solution of this problem was obtained by Pecsvaradi [10]. Later, this result was rediscovered by another group of researchers [11]. The shortest trajectory in such a problem is called the “Dubins path,” and the corresponding mobile object with limited maneuverability is called a “Dubins car.” (The first analogies with a car were apparently drawn by Isaacs.)

The notion of reachability set plays an important role in some applications [12, 13] using the Dubins car model. In the Cartesian coordinates \((x,y) \), the boundary of the time \(t \) reachability set is described in [14], and that of the time \(\le t \) reachability set, in [15]. Patsko et al. [16, 17] constructed and analyzed reachability sets in the three-dimensional state space for the Dubins car. In the present paper, we use some properties of the projection of the time \(t \) reachability set onto the Cartesian plane for a Dubins car (closedness, continuity of boundaries or their parts, and change in connectedness).

In contrast to [18], the present paper considers the nongame problem of the time-optimal interception of a moving target by a Dubins car. It is assumed that the target is moving along an arbitrary and previously known continuous trajectory. In contrast to [19, 20], the control is assumed to be a bounded function of time.

A similar problem simultaneously occurs in several papers where the authors restrict themselves to a partial solution. Necessary and sufficient conditions for capturing the target in the game of two cars were established for any initial conditions in [21]. In the nongame case of prescribed target movements, these conditions are sufficient. Sufficient conditions for an arc–straight-line trajectory to be an optimal path were established in [22]. These conditions impose constraints on the ratio of the minimum vehicle trajectory curvature radius to the distance between the target and the vehicle at the initial time. A control to intercept the target along a geodesic line drawn from the beginning of vehicle movement to the interception point was synthesized in [7, 23], the target being assumed to move along a straight line at a constant velocity. The paper [24] provides an algorithm for intercepting a target moving in a straight line by a Dubins car that chooses the shortest trajectory in the arc–straight-line class.

Meyer et al. [25, 26] identified several assertions related to the problem considered in the present paper. First, they established that if the target trajectory avoids unit disks tangent to the initial velocity vector of the Dubins car, then the time-optimal interception occurs along a geodesic line. Second, if the trajectory happens to fall into these circles, then there exist cases in which the optimal interception does not occur along a geodesic line. These authors also provided upper and lower bounds for the optimal interception time.

Problems of lateral interception of a moving target were considered in some papers. The angle of interception at the terminal time is fixed in such problems. For example, a solution of the problem of time-optimal interception at the right angle was obtained in [27], and the case of time-optimal interception by hitting the target, which moves in a circle, from behind was considered in [28]. It was assumed in both papers that the target is sufficiently far from the vehicle at the initial time.

2. STATEMENT OF THE PROBLEM

We describe a mobile plant by the Dubins car model [3, 15]. We select the units of measurement of length and time so that the velocity and the minimum radius of curvature of the car trajectory be equal to unity. In this case, the car dynamics in the Cartesian coordinates is described by the system

$$ \left \{\thinspace \begin {aligned} &\dot {x}=\cos \varphi ;&\quad &\dot {\varphi }=u\\ &\dot {y}=\sin \varphi ;&\quad &\big |u(t)\big |\leqslant 1. \end {aligned}\right .$$
(2.1)

Here \((x(t),y(t)) \) is the position of the car on the Cartesian plane, \(\varphi (t) \) is the angle between its velocity and the abscissa axis, and \(u(t) \) is the control at time \(t \). Set all initial conditions for system (2.1) to be fixed,

$$ x(0)=0,\quad y(0)=0,\quad \varphi (0)=\frac {\pi }2. $$
(2.2)

Let a continuous vector function \(E(t)=(x_E(t),y_E(t)) \) define the trajectory of motion of the target on the Cartesian plane. The terminal capture conditions are as follows:

$$ x_T\overset {\mathrm {def}}{=}x(T)=x_E(T),\quad y_T\overset {\mathrm {def}}{=}y(T)=y_E(T).$$
(2.3)

Here \(T\in \mathbb {R}^+_0\) is the time of motion from the initial point to the interception point. We pose the problem of capturing the target in minimum time as the optimal control problem

$$ J[u]\overset {\mathrm {def}}{=}\int \limits _0^Tdt\to \min _{u} $$

in the class of piecewise constant functions. It follows from Theorem 1 in the paper [14] that the class of piecewise constant functions will suffice.

In what follows, we use the notation in [11] to name the classes of trajectories: the letter \(C \) is assigned to the motion in a unit radius circle arc, and the letter \(S \) corresponds to the motion in a straight-line segment. Then \(CS \) is the class of trajectories consisting of a circle arc of unit radius and a segment, and \(CC\) is the class of trajectories consisting of two arcs of different circles of unit radius. All joints of arcs and segments are assumed to be smooth. In the present paper, it will be shown that the trajectories in the classes \(CS \) and \(CC \) suffice for the optimal interception. The letter \(C \) can be replaced by the letter \(L \) or \(R \) to indicate the direction of the turn (left or right turns, respectively). When moving in a straight line, \(u(t)=0 \); in the case of an \(L \)-turn, \(u(t)=1 \); for an \(R \)-turn, \(u(t)=-1 \). Unit radius circles tangent to the car velocity vector at the initial time will be denoted by \(\mathcal {D}_L\) and \(\mathcal {D}_R \).

By analogy with [14], we denote the reachability set of the Dubins car at time \(t \) on the plane of geometric coordinates by \(\mathcal {R}(t) \) and the boundary of this set by \(\mathcal {B}(t) \). The solution of the problem with a stationary target was fully studied in [3, 14, 15], where a detailed description of the set \(\mathcal {R}(t) \) [14] was obtained; therefore, instead of applying the Pontryagin maximum principle, we will use the properties of this set to synthesize an optimal control in the problem with a moving target. In Sec. 3, we write out algebraic relations describing \(\mathcal {B}(t) \); in the set \(\mathcal {B}(t) \), we will isolate the subset \(\mathcal {B}_G(t) \) of points to which the car can arrive at time \(t \) along a geodesic line; we will find a time threshold after which the optimal geodesic trajectories belong only to the class \(CS \). It will be shown in Sec. 4 that, except for only one situation, the optimal interception point lies on \(\mathcal {B}(t)\); we will derive equations for calculating the optimal interception time; an algebraic criterion will be given for interception to occur along a geodesic line. Section 5 describes an optimal control synthesis algorithm relying on the solution of nonlinear algebraic equations and also provides the results of numerical modeling of optimal interception for various target motion trajectories.

3. BOUNDARY OF THE REACHABILITY SET

Consider controls leading to the boundary \(\mathcal {B}(t) \) of the reachability set \(\mathcal {R}(t) \). It was shown in [14, p. 212] that any point in \(\mathcal {B}(t) \) can be reached along a trajectory of length \(t \) in the classes \(CS \) and \(CC \). The controls corresponding to these trajectories lead to \(\mathcal {B}(t)\) and can be concisely described using the following lemma, which naturally follows from Theorem 4 in the paper [14].

Lemma 1.

Each point of \(\mathcal {B}(T) \) can be reached at time \(T \) with the use of a control of the form

$$ u(t)= \bigg \{\thinspace \begin {aligned} &s,&\quad t&\in [0,\tau ]\\ &-\sigma s,&\quad t&\in (\tau , T], \end {aligned} $$
(3.1)

where \(s\in \{-1, 1\}\) , \( \sigma \in \{0, 1\}\) , \(\tau \in [0,T]\) , and \(\tau \leqslant 2\pi \) .

Indeed, the control (3.1) is associated with trajectories of the type \(CS\) if \(\sigma =0 \) and of the type \(CC \) if \(\sigma =1 \); the initial turn is to the left if \(s=1 \) and to the right if \(s=-1 \). The number \(\tau \) is called the control switching time.

In the sequel, by \(\mathcal {B}_\Lambda (t) \) we denote subsets \(\mathcal {B}(t) \) reachable at time \(t \) using a control of the type \(\Lambda {\thinspace \in \thinspace }\{LS,RS,LR,RL\}\). We also write \(\mathcal {B}_{CS}(t)=\mathcal {B}_{LS}(t)\cup \mathcal {B}_{RS}(t) \) and \(\mathcal {B}_{{CC}}(t)=\mathcal {B}_{LR}(t) \cup \mathcal {B}_{RL}(t)\). The subsequent exposition in this section essentially reproduces the results in [14] in a form more convenient for the interception problem and also refines them.

First, consider controls leading to \(\mathcal {B}_{CS}(T) \). Let us integrate the dynamic equations (2.1) with the initial conditions (2.2) for the control (3.1) with \(\sigma =0\),

$$ \left \{\thinspace \begin {aligned} sx_T+1&=-(T-\tau )\sin \tau +\cos \tau \\ y_T&=(T-\tau )\cos \tau +\sin \tau . \end {aligned}\right .$$
(3.2)

Define the sign function as

$$ \mathrm {sgn}~x\overset {\mathrm {def}}{=} \left \{\thinspace \begin {aligned} &1,\quad &x&>0\\ &0,\quad &x&=0\\ -&1,\quad &x&<0. \end {aligned}\right .$$

According to [3, 15], for \((x_T,y_T){\thinspace \in \thinspace }\mathcal {B}_{CS}(T) \) to hold, it is required that \(s=-\mathrm {sgn}~x_T \) except for the case in which \(x_T=0 \) and \(y_T<0 \). This means that within the time period \(\tau <2\pi \) the Dubins car should turn to the side of the ordinate axis where the point \((x_T,y_T)\) lies. If \((x_T,y_T) \) lies on the negative part of the ordinate axis, then the initial direction of turn is arbitrari; i.e., \(s=\pm 1\). Substituting \(s \) into the first equation in (3.2), we obtain the equation

$$ |x_T| = (T-\tau )\sin \tau -(\cos \tau -1)\geqslant 0,$$

which yields a constraint on the switching time \(\tau \) for a fixed \(T \). Let us introduce the notation

$$ \begin {aligned} x_{LS}(\tau , T)&\overset {\mathrm {def}}{=}-x_{RS}(\tau , T)\overset {\mathrm {def}}{=}-(T-\tau )\sin \tau +(\cos \tau -1);\\ y_{LS}(\tau , T)&\overset {\mathrm {def}}{=}y_{RS}(\tau , T)\overset {\mathrm {def}}{=}(T-\tau )\cos \tau +\sin \tau . \end {aligned}$$

Using this notation, we can write out an explicit form for the subsets \(\mathcal {B}_{CS}(T) \),

$$ \begin {aligned} \mathcal {B}_{LS}(T)&=\Big \{\big (x_{LS}(\tau , T), y_{LS}(\tau , T)\big )\thinspace \big | \:\tau \in [0,T],\:\tau <2\pi ,x_{LS}(\tau , T)\leqslant 0\Big \};\\ \mathcal {B}_{RS}(T)&=\Big \{\big (x_{RS}(\tau , T), y_{RS}(\tau , T)\big )\thinspace \big | \:\tau \in [0,T],\:\tau <2\pi ,x_{RS}(\tau , T)\geqslant 0\Big \}. \end {aligned} $$

Further, consider controls of the type \(CC \) leading to \(\mathcal {B}_{{CC}}(T) \). We integrate the dynamic equations (2.1) with the initial conditions (2.2) for the control (3.1) for \(\sigma =1\) and obtain the system

$$ \left \{\thinspace \begin {aligned} sx_T+1&=\big (2-\cos (T-\tau )\big )\cos \tau -\sin (T-\tau )\sin \tau \\ y_T&=\big (2-\cos (T-\tau )\big )\sin \tau +\sin (T-\tau )\cos \tau . \end {aligned}\right . $$
(3.3)

According to [14, p. 211], for \((x_T,y_T){\thinspace \in \thinspace }\mathcal {B}_{{CC}}(T)\) to hold, it is required that \( s=\mathrm {sgn}\;x_T\) for \(x_T\neq 0 \); i.e., within the time period \(\tau \leqslant \pi /2 \), the Dubins car should turn in the direction opposite to the side of the ordinate axis where the point \((x_T,y_T) \) lies. If, however, \(x_T=0 \), then the direction of the first turn is arbitrary; i.e., \(s=\pm 1 \). Substituting \(s \) into the first equation in (3.3), we obtain the equation

$$ |x_T| = \big (2-\cos (T-\tau )\big )\cos \tau -\sin (T-\tau )\sin \tau - 1\geqslant 0,$$
(3.4)

which gives a constraint on the switching time \(\tau \) for a fixed \(T \).

Fig. 1.
figure 1

Evolution of the set \(\mathcal {B}(t)\), the boundary of the reachability set.

Full size image

By following a trajectory of the type \(CC\), one can only get on the boundary of the reachability set for \(T<\mathcal {T}^*=2\pi +\mathrm {arccos}(23/27) \) [14, p. 215]. The set \(\mathcal {B}_{{CC}}(t) \) “shrinks” to some point \(E^* \) in the sense that starting from some time \(t \), an arbitrary \(\varepsilon \)-neighborhood of the point \(E^* \) contains all points in \(\mathcal {B}_{{CC}}(t) \). A trajectory of the type \(CC \) with \(\tau =\mathrm {arccos}(1/3) \) [14, p. 215] leads to the “shrinking” point. The position of the point \(E^* \) can be calculated by substituting \(\tau =\mathrm {arccos}(1/3)\) and \(T=\mathcal {T}^* \) into Eqs. (3.3); this yields \(E^*=(0{,}2\sqrt {2}/3) \).

We introduce the notation

$$ \begin {aligned} x_{LR}(\tau , T)&\overset {\mathrm {def}}{=}-x_{RL}(\tau , T)\overset {\mathrm {def}}{=}\big (2-\cos (T-\tau )\big )\cos \tau -\sin (T-\tau )\sin \tau - 1;\\ y_{LR}(\tau , T)&\overset {\mathrm {def}}{=}y_{RL}(\tau , T)\overset {\mathrm {def}}{=}\big (2-\cos (T-\tau )\big )\sin \tau +\sin (T-\tau )\cos \tau . \end {aligned} $$

According to [14, p. 214], for \(T>2\pi \) the boundaries of the inner cavity consist only of the points \( \mathcal {B}_{{CC}}(T)\); therefore, the point with the least ordinate in \(\mathcal {B}_{{CC}}(T) \) lies not lower than \(T-2\pi \). (Otherwise, a trajectory of the type \(CS \) with \(\tau =2\pi \) would have led to the point with the least ordinate.) Now we are in a position to write out an explicit form for the subsets \(\mathcal {B}_{{CC}}(T) \) for \(T<\mathcal {T}^* \),

$$ \begin {aligned} \mathcal {B}_{LR}(T)&=\Big \{\big (x_{LR}(\tau , T), y_{LR}(\tau , T)\big )\thinspace \big | \:\tau \in [0,T], \tau \leqslant \frac {\pi }{2},x_{LR}(\tau , T)\geqslant 0,y_{LR}(\tau , T)\geqslant T-2\pi \Big \}; \\ \mathcal {B}_{RL}(T)&=\Big \{\big (x_{RL}(\tau , T), y_{RL}(\tau , T)\big )\thinspace \big | \:\tau \in [0,T], \tau \leqslant \frac {\pi }{2},x_{RL}(\tau , T)\leqslant 0,y_{RL}(\tau , T)\geqslant T-2\pi \Big \}. \end {aligned}$$

In other cases, we set \(\mathcal {B}_{{CC}}(T)=\varnothing \). The evolution of the boundary of the reachability set is illustrated by Fig. 1.

Let us describe the set of points \(\mathcal {B}_G(T)\subset \mathcal {B}(T)\) which the Dubins car can reach at time \(T \) along a geodesic line. According to [1, 3], the geodesic line belongs to the class \(CC\) if the terminal point is inside the circle \(\mathcal {D}_L\) or \(\mathcal {D}_R \) and to the class \(CS \) if the terminal point is outside these circles. Taking into account the additional condition that all points \(\mathcal {B}_{CS}(t) \) lie outside the circles \(\mathcal {D}_L \) and \(\mathcal {D}_R \), we obtain

$$ \mathcal {B}_G(T) = \mathcal {B}_{CS}(T)\cup \Big \{(x, y)\in \mathcal {B}_{{CC}}(T)\thinspace \big |\:\big (|x|-1\big )^2+y^2<1\Big \}. $$
(3.5)

Lemma 2.

The time \(\mathcal {T}=2(\pi +\mathrm {arctan}\sqrt {3/125})\) is the minimum time such that the set \(\mathcal {B}_G(T) \) consists only of the elements of the set \(\mathcal {B}_{CS}(T) \) for any \( T\geqslant \mathcal {T}\) .

Fig. 2.
figure 2

Illustration of behavior of the implicit function \(\chi (\tau ,T) = 0\). The domain where \(\chi (\tau , T) > 0\) is black, and the domain where \(\chi (\tau ,T) < 0\) is white.

Full size image

Proof. According to the expression (3.5), for \(\mathcal {B}_G(T)\) we need to show that

$$ {\big \{(x, y)\in \mathcal {B}_{{CC}}(T)|\:(|x|-1)^2+y^2<1\big \}=\varnothing }\text { for }{T\geqslant \mathcal {T}}.$$

Owing to symmetry, we consider only the case of the right half-plane. It was noted earlier that \(\tau \leqslant \pi /2\) for trajectories leading to \(\mathcal {B}_{{CC}}(T) \). If \(\tau >\pi /3 \), then the second arc of the trajectory \(LR \) does not meet the circle \(\mathcal {D}_R \) for any \(T \). Hence each geodesic line leading into \(\mathcal {D}_R \) has the switching time \(\tau \leqslant \pi /3 \). Let us substitute the second relation in (3.3) and relation (3.4) into

$$ \big (|x_T|-1\big )^2 + y_T^2 < 1 $$

to obtain

$$ \chi (\tau ,T)\overset {\mathrm {def}}{=}2(\cos \tau -1)+\cos (T-\tau )-\cos (T-2\tau )>0.$$
(3.6)

Since \(\mathcal {B}_{{CC}}(T)=\varnothing \) for \(T\geqslant \mathcal {T}^*\), we need to show that inequality (3.6) does not hold for any \(\tau \in [0,\pi /3] \) and \(T\in [\mathcal {T},\mathcal {T}^*]\). The function \(\chi (\tau ,T) \) is monotone decreasing with respect to \(T \) for any \(\tau \in (0,\pi /3] \). Let us analyze the graph of the implicit function given by the equation \(\chi (\tau ,T)=0\) for \(T \) (Fig. 2). This implicit function has a single maximum on the rectangle \(\tau \in (0,\pi /3]\), \(T\in [2\pi ,\mathcal {T}^*] \). The position of this maximum is determined by the solution of the system of equations

$$ \left \{\thinspace \begin {aligned} 2(\cos \tau -1)+\cos (T-\tau ) &= \cos (T-2\tau )\\ -2\sin \tau +\sin (T-\tau ) &= 2\sin (T-2\tau ). \end {aligned}\right .$$

Solving this system on the rectangle under consideration is rather bulky. By a straightforward substitution we can verify that its solution is the pair \(\tau =2\:\mathrm {arctan}\sqrt {5/27} \), \(T=\mathcal {T} \). The proof of the lemma is complete. \(\quad \blacksquare \)

Fig. 3.
figure 3

Boundary \(\mathcal {B}(t)\) of the reachability set at time \(t = 11\pi /6 \). All six points of matching smooth boundaries are present on the boundary at this time.

Full size image

4. SOLUTION OF THE INTERCEPTION PROBLEM

Let us show that the optimal point of interception of the moving target lies on the boundary \( \mathcal {B}(t)\) of the reachability set \(\mathcal {R}(t)\) except for one case. According to [14, p. 208], the set \(\mathcal {R}(t) \) is closed and bounded for all positive \(t \). The reachability set boundary \(\mathcal {B}(t) \) consists of several smooth parts. These parts are continuously connected with one another at at most six points at each time \(t \) (Fig. 3). For \(t\in (0{,}3\pi /2+1) \), there are four such points (a), (b), (c), and (d); for \(t=3\pi /2+1 \), there are five points: point (e) coincides with point (f); for \( t\in (3\pi /2+1{,}2\pi )\), there are six points; for \(t\in [2\pi ,\thinspace \mathcal {T}^*)\), there are four points: points (c), (d), and (e) coincide at \(t=2\pi \); for \(t\geqslant \mathcal {T}^*\), there are two points—(a) and (f).

A set-valued mapping \(\mathcal {B}\) is said to be lower semicontinuous at time \(t_0\) if for each \(\varepsilon >0 \) and each point \(P_0\in \mathcal {B}(t_0) \) there exists a \(\delta >0 \) such that for each \(t:|t-t_0|<\delta \) there exists a point \(P\in \mathcal {B}(t) \) such that \(\lVert P-P_0 \rVert < \varepsilon \). A set-valued mapping \(\mathcal {B} \) is upper semicontinuous at time \(t_0 \) if for each \(\varepsilon >0 \) there exists a \(\delta >0 \) such that for each \(t:|t-t_0|<\delta \) and each point \(P\in \mathcal {B}(t) \) there exists a point \(P_0\in \mathcal {B}(t_0) \) such that \(\lVert P-P_0 \rVert < \varepsilon \). If a set-valued mapping \(\mathcal {B} \) is lower and upper semicontinuous at a point \(t_0 \), then it is said to be continuous at this point.

Lemma 3.

The set-valued mapping \( \mathcal {B}\) determining the evolution of the boundary of the reachability set is continuous at each time \(t>0 \) except for \( t=\mathcal {T}^*\) , where the mapping \(\mathcal {B} \) is lower semicontinuous.

Proof. First, we show that all points \(\mathcal {B}(t_0)\) except for (a)–(f) have a finite velocity of motion on the plane for each \(t_0>0\). Fix a \( P_0=(x_0,y_0)\in \mathcal {B}(t_0)\) and consider two cases. In the first case, \(P_0\in \mathcal {B}_{CS}(t_0) \), with the point \(P_0 \) not coinciding with points (a), (c)–(f). In accordance with (3.2), one has the system

$$ \left \{\thinspace \begin {aligned} x_0&= s_0(-(t_0-\tau _0)\sin \tau _0+\cos \tau _0 - 1)\\ y_0&= (t_0-\tau _0)\cos \tau _0+\sin \tau _0. \end {aligned}\right . $$

Taking the partial derivatives of the first and second equation in this system with respect to \(t_0\), squaring them, and adding, we obtain the equation

$$ \left (\frac {\partial x_0}{\partial t_0}\right )^2 + \left (\frac {\partial y_0}{\partial t_0}\right )^2 = 1. $$

In the second case, \(P_0\in \mathcal {B}_{{CC}}(t_0)\), with the point \(P_0 \) not coinciding with points (b)–(d). In accordance with (3.3), one has the system

$$ \left \{\thinspace \begin {aligned} x_0 &= s_0((2-\cos (t_0-\tau _0))\cos \tau _0-\sin (t_0-\tau _0)\sin \tau _0 - 1)\\ y_0 &= (2-\cos (t_0-\tau _0))\sin \tau _0+\sin (t_0-\tau _0)\cos \tau _0. \end {aligned}\right .$$

We again take the partial derivatives of the first and second equations in this system with respect to \(t_0 \), square them, and add to obtain the equation

$$ \left (\frac {\partial x_0}{\partial t_0}\right )^2 + \left (\frac {\partial y_0}{\partial t_0}\right )^2 = 1.$$

With the unit velocity, there always exists a \(\delta =\varepsilon >0\) and a point \(P\in \mathcal {B}(t) \) such that for \(|t-t_0|<\delta \) one has \(\lVert P-P_0\rVert \leqslant |t-t_0|<\delta =\varepsilon \).

Now let \(P_0\) be one of points (a)–(f). By virtue of the fact that \(P_0\) is adjacent to the continuous lines of the set \(\mathcal {B}(t_0)\), for any \(t_0 \) there exists a point \(P_0^{\prime }\in \mathcal {B}(t_0)\) distinct from (a)–(f) such that \(\lVert P_0-P_0^{\prime } \rVert < \varepsilon /2\), and for \( P_0^{\prime }\), owing to what has been proved above, there exists a \(P\in \mathcal {B}(t) \) with \(\lVert P-P_0^{\prime }\rVert <\varepsilon /2\). Using the triangle inequality, we obtain \(\lVert P-P_0 \rVert < \varepsilon \); this proves the lower semicontinuity.

Since \(\mathcal {B}(t)\) consists of continuous parts, it follows that for each point \(P\!\in \!\mathcal {B}(t) \) there exists a \(P^{\prime }\!\in \!\mathcal {B}(t)\), distinct from (a)–(f), with \(\lVert P-P^{\prime }\rVert \!\leqslant \! \varepsilon /2 \). If \(t_0\!\neq \!\mathcal {T}^* \), then, taking \(\delta \!=\!\min (|\mathcal {T}^*-t_0|,\varepsilon /2)\), for each time \( t:|t-t_0|<\delta \) and for each point \(P\in \mathcal {B}(t)\) there exists a point \(P_0\in \mathcal {B}(t_0) \) such that

$$ \lVert P-P_0 \rVert \leqslant \lVert P-P^{\prime } \rVert + \lVert P^{\prime }-P_0 \rVert \leqslant \varepsilon /2 + |t-t_0| < \varepsilon /2 + \delta \leqslant \varepsilon ; $$

this proves the upper semicontinuity for all \(t_0>0 \) except for \(t_0=\mathcal {T}^* \). At time \(t_0=\mathcal {T}^* \), the set \(\mathcal {B}_{{CC}}(t_0) \) separated from \(\mathcal {B}_{CS}(t_0) \) disappears, and therefore, the upper semicontinuity is absent at this time. The proof of the lemma is complete.\(\quad \blacksquare \)

Assertion 1.

If the optimal interception of the target is possible in time \(T\) , then the optimal interception point lies on \(\mathcal {B}(T) \) except for the case where the optimal interception point is \(E^*=(0, 2\sqrt {2}/3) \) and the optimal interception time is \(T=\mathcal {T}^* \) .

Proof. If \(E(T)=E^* \) and \(T=\mathcal {T}^* \), then the optimal interception occurs along a trajectory of the type \(RL\) or \(LR \) but not on \(\mathcal {B}(T) \), because, by virtue of the description of the boundary of the reachability set given in Sec. 3, one has \( E^*\notin \mathcal {B}(\mathcal {T}^*)\). Now let \(E(T)\neq E^* \) or \(T\neq \mathcal {T}^* \). Assume that \(E(T) \) is an interior point of \(\mathcal {R}(T) \). Then there exists a ball \(\mathcal {O} \) centered at the point \(E(T) \) which lies entirely inside \(\mathcal {R}(T) \), and each point of the boundary of such a ball is separated from \( \mathcal {B}(T)\) by at least \(\varepsilon >0 \). By virtue of Lemma 3 and the “shrinking” of \(\mathcal {B}_{{CC}}(t) \) to \(E^*\neq E(T) \) as \(t\to \mathcal {T}^* \), there exists a \(\delta >0 \) such that for any \(t\in (T-\delta , T+\delta ) \) the points of the boundary \(\mathcal {B}(t) \) do not fall in this ball, and therefore, \(\mathcal {O}\subset \mathcal {R}(t)\). By virtue of the continuity of \( E(t)\), one can choose \(\delta \) small enough that \(E(t)\in \mathcal {O} \) holds. Hence \(E(t)\in \mathcal {R}(t) \); this contradicts the fact that \(T \) is the minimum interception time, and consequently, \( E(T)\) lies on the boundary \(\mathcal {R}(T) \). The proof of the assertion is complete. \(\quad \blacksquare \)

Let us derive algebraic equations for the optimal interception time. If the optimal interception occurs along a trajectory of the type \(CS \), then, in accordance with (2.3) and (3.2), the optimal \(\tau \) and \(T \) are determined from the system

$$ \left \{\thinspace \begin {aligned} 1-|x_E(T)|=-(T-\tau )\sin \tau +\cos \tau \\ y_E(T)=(T-\tau )\cos \tau +\sin \tau . \end {aligned}\right .$$
(4.1)

Squaring the expressions in (4.1) and adding them, after easy transformations and considering the fact that \(T\geqslant \tau \), we obtain

$$ T - \tau = \sqrt {\Big (1-\big |x_E(T)\big |\Big )^2+y_E^2(T)-1}.$$
(4.2)

Let us introduce the notation

$$ \begin {aligned} \alpha _{C}(T)&\overset {\mathrm {def}}{=}\frac {1-\big |x_E(T)\big |+y_E(T)\sqrt {\Big (1-\big |x_E(T)\big |\Big )^2+y_E^2(T)-1}}{\Big (1-\big |x_E(T)\big |\Big )^2+y_E^2(T)},\\ \alpha _{S}(T)&\overset {\mathrm {def}} {=}\frac {y_E(T)-\Big (1-\big |x_E(T)\big |\Big ) \sqrt {\Big (1-\big |x_E(T)\big |\Big )^2+y_E^2(T)-1}} {\Big (1-\big |x_E(T)\big |\Big )^2+y_E^2(T)}; \end {aligned} $$

then, after substituting (4.2) into (4.1) and solving system (4.1) for \(\tau \in [0,2\pi ) \), we obtain

$$ \tau =\theta _{CS}(T)\overset {\mathrm {def}}{=} \left \{\thinspace \begin {aligned} &\arccos {\alpha _{C}(T)},&\quad \alpha _{S}(T)&\geqslant 0\\ &2\pi -\arccos {\alpha _{C}(T)},&\quad \alpha _{S}(T)&<0.\\ \end {aligned}\right . $$

Substituting the value of \(\tau =\theta _{CS}(T) \) into (4.2), we obtain an equation for the optimal interception time. Thus, the optimal interception time \(\mathcal {T}_{CS}[x_E,y_E] \) is the least nonnegative root of the following equation for \(T \):

$$ T-\theta _{CS}(T)-\sqrt {\Big (1-\big |x_E(T)\big |\Big )^2+y_E^2(T)-1} = 0.$$
(4.3)

If this equation does not have nonnegative roots, then we assume that \(\mathcal {T}_{CS}[x_E,y_E]=+\infty \). Ill-defined operations such as division by zero, taking the square root of a negative number, etc. may arise for some \(T \) on the left-hand side in the expression (4.3). In such cases, optimal capture at time \(T \) along a trajectory of the type \(CS \) is impossible. For example, if we assume that the optimal interception point lies inside the circle \(\mathcal {D}_L\) or \(\mathcal {D}_R \), then the optimal interception cannot be performed along a trajectory of the type \(CS\), because the calculation of the left-hand side of (4.3) involves taking the square root of a negative number; therefore, in this case we assume that \(\mathcal {T}_{CS}[x_E,y_E]=+\infty \).

Now let us carry out similar reasoning for the case of optimal interception along a trajectory of the type \(CC\). In accordance with (2.3) and (3.3), the optimal \(\tau \) and \(T \) are determined by the system

$$ \left \{\thinspace \begin {aligned} \big |x_E(T)\big |+1&=\big (2-\cos (T-\tau )\big ) \cos \tau -\sin (T-\tau )\sin \tau \\ y_E(T)&=\big (2-\cos (T-\tau )\big )\sin \tau +\sin (T-\tau )\cos \tau . \end {aligned}\right .$$
(4.4)

Squaring the expressions in (4.4) and adding them, after easy transformations we obtain

$$ \cos (T-\tau )=\frac {5-\Big (1+\big |x_E(T)\big |\Big )^2-y_E^2(T)}{4}\overset {\mathrm {def}}{=}\alpha (T). $$
(4.5)

After substituting (4.5) into (4.4) and solving system (4.4) for \(\tau \in [0,\pi /2] \), we, generally speaking, obtain two solutions,

$$ \tau =\theta ^{\pm }_{{CC}}(T)\overset {\mathrm {def}}{=}\arccos {\frac {\Big (1+\big |x_E(T)\big |\big )\big (2-\alpha (T)\big )\pm y_E(T)\sqrt {1-\alpha ^2(T)}}{\Big (1+\big |x_E(T)\big |\big )^2+y^2_E(T)}}.$$

It can be shown that if \( T\leqslant \pi \), then \(\tau =\theta ^+_{{CC}}(T) \), and if \(T\geqslant \pi +\mathrm {arccos}(1/3)\), then \(\tau =\theta ^-_{{CC}}(T) \).

Separately considering the cases of \(\tau =\theta _{{CC}}^+(T) \) and \(\tau =\theta _{{CC}}^-(T) \), after the substitution of \(\tau \) into (4.5) and the inversion of cosine with allowance for the fact that \(T-\tau \in [0,2\pi ]\), we will obtain two equations for the optimal interception time,

$$ \begin {aligned} T-\theta ^+_{{CC}}(T)-\arccos {\alpha (T)} &= 0,\\ T-\theta ^-_{{CC}}(T)-2\pi +\arccos {\alpha (T)} &= 0. \end {aligned} $$
(4.6)

The least nonnegative roots of these two equations will be denoted by \( \mathcal {T}^+_{{CC}}[x_E,y_E]\) and \(\mathcal {T}^-_{{CC}}[x_E,y_E]\), respectively. In the case of no roots, we assume that \(\mathcal {T}^{\pm }_{{CC}}[x_E,y_E]=+\infty \). Just as in the case of trajectories of the type \(CS \), ill-defined operations may arise when calculating the left-hand side of either equation in (4.6) for some \(T \). If ill-defined operations arise when calculating two expressions at once, then optimal capture at time \(T \) along a trajectory of the type \(CC \) is impossible. If ill-defined operations arise when calculating the first expression and the second expression turns into an identity after the substitution of \(T \), then optimal interception is performed with the switching time \( \theta _{{CC}}^-(T)\) and vice versa. The optimal interception time is determined by the choice of the least of two times, \( {\mathcal {T}_{{CC}}[x_E,y_E] =\min (\mathcal {T}^{+}_{{CC}}[x_E,y_E], \mathcal {T}^{-}_{{CC}}[x_E,y_E])} \). For known \(T \), the optimal switching time is determined as follows:

$$ \tau =\theta _{{CC}}(T)\overset {\mathrm {def}}{=} \left \{\thinspace \begin {aligned} &\theta ^+_{{CC}}(T),&\quad \mathcal {T}^+_{{CC}}[x_E,y_E]&\leqslant \mathcal {T}^-_{{CC}}[x_E,y_E]\\ &\theta ^-_{{CC}}(T),&\quad \mathcal {T}^+_{{CC}}[x_E,y_E]&>\mathcal {T}^-_{{CC}}[x_E,y_E]. \end {aligned}\right . $$

If the interception is impossible, then Eqs. (4.3) and (4.6) do not have nonnegative solutions. If the interception is possible, then at least one of Eqs. (4.3) and (4.6) has a nonnegative solution, because the Dubins car is completely controllable in the trajectory classes \(CS \) and \(CC \).

If the optimal interception point lies on the ordinate axis, then the initial control sign can be selected arbitrarily (by virtue of the symmetry of the problem). In accordance with Lemma 1, if the optimal trajectory is a line of the type \(CS \), then the optimal control has the form

$$ u(t)=u^o_{CS}(t)\overset {\mathrm {def}}{=} \left \{\thinspace \begin {aligned} &-\mathrm {sgn}\:x_E\big (\mathcal {T}_{CS}[x_E,y_E]\big ),&t&<\theta _{CS}\big (\mathcal {T}_{CS}[x_E,y_E]\big ),\:x_E\big (\mathcal {T}_{CS}[x_E,y_E]\big )\neq 0\\ &\pm 1,&t&<\theta _{CS}\big (\mathcal {T}_{CS}[x_E,y_E]\big ),\:x_E\big (\mathcal {T}_{CS}[x_E,y_E]\big )=0\\ &0,&t&\geqslant \theta _{CS}\big (\mathcal {T}_{CS}[x_E,y_E]\big ).\\ \end {aligned}\right .$$

If the optimal trajectory is a line of the type \(CC\), then the optimal control has the form

$$ u(t)=u^o_{{CC}}(t)\overset {\mathrm {def}}{=} \left \{\thinspace \begin {aligned} &\mathrm {sgn}\:x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ),&t&<\theta _{{CC}}\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ),\:x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big )\neq 0\\ &-\mathrm {sgn}\:x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ),&t&\geqslant \theta _{{CC}}\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ),\:x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big )\neq 0\\ &\pm 1,&t&<\theta _{{CC}}\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ),\:x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big )=0\\ &\mp 1,&t&\geqslant \theta _{{CC}}\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ),\:x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big )=0.\\ \end {aligned}\right . $$

The sign \(\pm \) in the above expressions can be selected in an arbitrary way.

Let the time of interception of a target whose motion is known in advance be finite. Then the following assertion holds.

Assertion 2.

The optimal control in the problem of time-optimal interception of a moving target by the Dubins car has the form

$$ u(t)=u^o(t)\overset {\mathrm {def}}{=}\left \{\thinspace \begin {aligned} &u^o_{CS}(t),&\quad \mathcal {T}_{CS}[x_E,y_E]&\leqslant \mathcal {T}_{{CC}}[x_E,y_E]\\ &u^o_{{CC}}(t),&\quad \mathcal {T}_{CS}[x_E,y_E]&>\mathcal {T}_{{CC}}[x_E,y_E]. \end {aligned}\right . $$

Based on the description of \(\mathcal {B}_G(t)\) and Assertion 1, one can readily state an algebraic criterion for the interception along a geodesic line to be optimal. To this end, it is necessary and sufficient to require that the optimal interception point lies on \(\mathcal {B}_G(T) \).

Assertion 3.

The optimal interception trajectory is a geodesic line if and only if

$$ {\mathcal {T}_{CS}[x_E,y_E]\leqslant } {\mathcal {T}_{{CC}}[x_E,y_E]}\text { or } \Big (\big |x_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big )\big |-1\Big )^2 + y^2_E\big (\mathcal {T}_{{CC}}[x_E,y_E]\big ) < 1.$$

Theorem 5 in [26] is a special case of this assertion. Indeed, if the optimal interception is possible and \(\mathcal {T}_{CS}[x_E,y_E]\leqslant \mathcal {T}_{{CC}}[x_E,y_E] \), then it occurs along a trajectory of the type \(CS \) and finishes outside the circles \(\mathcal {D}_L \) and \(\mathcal {D}_R \). In this case, the requirement for the target trajectory not to have its parts inside \(\mathcal {D}_L\) and \(\mathcal {D}_R \) drops out.

Fig. 4.
figure 4

Trajectory of optimal interception (solid line) for seven different versions of the target motion (dashed line); \(E_{i}(t) = E_{i0} + \vec {v}_{i}t\), where \(\vec {v}_{i} = (v_{i} \cos \varphi _{i}, v_{i} \sin \varphi _{i})\), \(i\in \{1, 2,\ldots , 7\}\).

Full size image

5. NUMERICAL EXAMPLES

Using Assertion 2 and the expressions (4.3) and (4.6), one can construct an optimal trajectory of interception of the moving target. Let us describe the sequence of actions that makes such a construction possible. At the first step, we need to find three minimum nonnegative roots of Eqs. (4.3) and (4.6). If some of these equations does not have roots, then we take the root to be equal to \(+\infty \). At the end of the first step, we have three values \(\mathcal {T}_{CS}[x_E,y_E]\), \(\mathcal {T}_{{CC}}^+[x_E,y_E] \), and \(\mathcal {T}_{{CC}}^-[x_E,y_E] \). If all three values are equal to \(+\infty \), then the interception is impossible. Otherwise, the three values calculated suffice to produce an optimal control using Assertion 2.

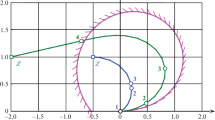
The target motion trajectory can be any continuous line. For simplicity of illustrations, we will assume that the target moves in a straight line at a constant speed. Figure 4 shows seven different cases of interception. For \( i=1\) the target starts its motion from the disk \(\mathcal {D}_L \) at a sufficiently small speed that allows the target to avoid encounter on the set \(\mathcal {B}_{CS}(t) \) and delay interception to the time of falling on \(\mathcal {B}_{{CC}}(T)\). For \(i=2 \) the target trajectory does not meet the circles \(\mathcal {D}_L \) and \(\mathcal {D}_R \); therefore, the optimal interception occurs along a trajectory of the type \(CS\). For \(i=3 \) the target starts its motion from \(\mathcal {D}_R \), and the optimal interception, just as in the case of \(i=2 \), occurs along a geodesic line, because the conditions in Assertion 3 are satisfied. For \(i=4 \) the motion starts from within \(\mathcal {D}_R \), and the optimal interception occurs in \(\mathcal {D}_L \). This case is notable in that the trajectory of the target can intersect the optimal trajectory of the car before interception. For \(i=5 \) the target motion starts outside the circles \(\mathcal {D}_L \) and \(\mathcal {D}_R \), and the optimal interception occurs inside \(\mathcal {D}_R \) along a trajectory of the class \(CC \). For \(i=6 \) and \(i=7 \) the target has a velocity greater than or equal to that of the car; despite this fact, the car is still capable of intercepting the target.

The examples provided supplement the list of special cases of optimal interception available in the literature. Note that the cases of \(i\in \{1,2,3,6,7\} \) illustrate the fact that if the optimal interception point lies outside the circles \(\mathcal {D}_L\) and \( \mathcal {D}_R\), then the optimal car trajectory can be both in the class \(CC\) (e.g., for \(i\in \{1,6,7\}\) ) and in the class \(CS\) (for \( i\in \{2,3\}\)). If, however, the optimal interception point lies outside the circles \(\mathcal {D}_L\) and \( \mathcal {D}_R\), then the optimal car trajectory belongs only to the class \(CC\).

6. CONCLUSIONS

We have obtained the closed-form expressions (4.3) and (4.6) allowing one to determine the minimum interception time for the problem of time-optimal interception of a moving target by a Dubins car. Using Lemma 3, we show that the set-valued mapping \(\mathcal {B} \) defining the evolution of the reachability set boundary is continuous except for one time. Assertions 1 and 2 allow determining the position of the optimal interception point and the type of optimal control. The above expressions make it possible to solve the problem of time-optimal interception for an arbitrary continuous and predetermined trajectory of the target. The expressions (4.3) and (4.6) can be simplified, and the optimal interception time can be expressed explicitly if the class of target trajectories is narrower than the class of continuous lines (for example, a point if the target is at rest).

Assertion 3 contains an algebraic criterion for the optimality of interception along a geodesic line. For any time, Lemma 2 defines the threshold value of the interception time past which the optimal geodesic trajectories belong only to the class \(CS \). However, for some cases of target motion, the optimal interception does not always follow a geodesic line; this is also illustrated by numerical examples and modeling.