Abstract
The diffusion of electric vehicles suffers from immature and expensive battery technologies. Repurposing electric vehicle batteries for second-life application scenarios may lower the vehicles’ total costs of ownership and increases their ecologic sustainability. However, identifying the best – or even a feasible – scenario for which to repurpose a battery is a complex and unresolved decision problem. In this exaptation research, we set out to design, implement, and evaluate the first decision support system that aids decision-makers in the automobile industry with repurposing electric vehicle batteries. The exaptation is done by classifying decisions on repurposing products as bipartite matching problems and designing two binary integer linear programs that identify (a) all technical feasible assignments and (b) optimal assignments of products and scenarios. Based on an empirical study and expert interviews, we parameterize both binary integer linear programs for repurposing electric vehicle batteries. In a field experiment, we show that our decision support system considerably increases the decision quality in terms of hit rate, miss rate, precision, fallout, and accuracy. While practitioners can use the implemented decision support system when repurposing electric vehicle batteries, other researchers can build on our results to design decision support systems for repurposing further products.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Imagine that by the year 2020, electric vehicles are a widespread technology. Automobile companies manage electric vehicles and their decisive component – a lithium-based electric vehicle battery (henceforth battery) that is a complex power storage device for supplying an electric vehicle with electric current (Burke, 2009) – along their entire lifecycle.
Because of a deterioration of their cell materials (Ebner et al, 2013; Sasaki et al, 2013), batteries should be removed from electric vehicles once their capacity has dropped below 80% of their initial capacity (limiting a vehicle’s range) or their internal resistance has doubled (impeding a vehicle’s acceleration and charging power) (Burke, 2009; Knowles & Morris, 2014; Waag et al, 2013). Current battery technology is estimated to reach this point after having powered an electric vehicle for some 100,000 km or after about eight years of operation (Ahmadi et al, 2014). With rising sales figures of electric vehicles (Shahan, 2014), the automobile industry can expect a considerable number of batteries to be returned soon (Lache et al, 2008; Pillot, 2012). The global market for used batteries is estimated to grow from $16 million in 2014 to more than $2 billion in 2022 (EVWorld.com Inc., 2011) and to around $3 billion in 2035 (PRNewswire, 2014).
BMW’s (evworld.com, 2013), Chevrolet’s (Howard, 2013), and Nissan’s (St. John, 2015) proof-of-concept projects have shown that batteries can be repurposed as energy storage solutions. Related research has investigated additional stationary second-life application scenarios, including applications as energy storage in a smart home (Sachenbacher et al, 2012), as uninterruptible power supply (Cready et al, 2003), as energy grid stabilization (Patten et al, 2011; Knowles & Morris, 2014), or as residential load levelling (Burke, 2009; Beer et al, 2012). However, the decision to assign an individual battery to the most suitable application scenario is so complex and unexplored that there has been no research in this area. At the same time, the literature on decision support systems (DSSs) provides a rich array of methods that may solve decision problems related to repurposing batteries.
The purpose of this paper is to design a DSS that aids decision-makers with matching used batteries to second-life application scenarios (henceforth scenarios). In line with the generic architecture of a model-driven DSS (Power, 2004; Power & Sharda, 2007), the system contains a database of batteries and scenarios, provides decision models for optimal matching, and features a graphical user interface. The paper is exaptation research (Gregor & Hevner, 2013) since it seeks to apply and modify established methods from the DSS field to solve a new and unexplored decision problem. In line with research guidelines prescribed in the literature on design science research (DSR) (Hevner et al, 2004; Peffers et al, 2008; Gregor & Hevner, 2013), the IT artifact has been designed and evaluated in a cyclic search process.
This research offers descriptive and prescriptive contributions. First, we characterize the repurposing of used batteries to scenarios as an unresolved decision task. We explain how the decision process works and why finding fitting batteries and scenarios classifies as a bipartite matching problem. Second, based on adopted methods and tools for solving bipartite matching problems, we design two decision models that (a) identify the technical fit between all products and all scenarios and (b) provide an optimal solution for matching many products to many scenarios. These generic decision models inform decision processes for repurposing any class of products in physical environments. Third, we design the first DSS to support the entire decision process, from modeling the available products and scenarios to assigning each individual product to a scenario. Fourth, we parameterize the decision models for repurposing batteries, based on natural laws and empirical data. In a field experiment, we show that the designed IT artifact efficiently solves the decision problem and that it substantially increases decision quality. Practitioners can use the designed IT artifact for repurposing used batteries. Other researchers can use the artifact and the parametrization process as blueprints for designing DSS to repurpose products other than batteries.
The remainder of the paper is structured in line with the DSR publication schema proposed by Gregor & Hevner (2013). In “Research background”, we characterize repurposing batteries as an unresolved decision problem, identify the underlying class of decision problems, and identify suitable artifacts for the exaptation. In “Research method”, we describe and justify the research process. In "Artifact description", we present the designed and implemented DSS. In “Model parametrization, demonstration, and evaluation”, we parameterize the decision models for repurposing used batteries and evaluate the system’s effectiveness and efficiency. “Discussion” provides a discussion of the paper’s contributions and limitations, and “Conclusions” concludes the paper.
Research background
Repurposing electric vehicle batteries
An electric vehicle battery is an energy storage system that mainly consists of a modular battery pack (including cells that provide electric power), a battery management system for monitoring and controlling the pack, a thermal management system, and a battery case (Schlick et al, 2011; Klör et al, 2015b). Currently, the battery accounts for about 20–40% of an electric vehicle’s costs (e.g., Nykvist & Nilsson, 2015).
Driving and charging the vehicle cause the battery to age. After about eight to ten years of operation or around 100,000 km driven, battery aging noticeably limits a vehicle’s range (capacity fade) (Ahmadi et al, 2017), acceleration, and fast charging capability (both power fade) so that car manufacturers offer a battery replacement. Different driving patterns, operating temperatures, and charging rates (Price et al, 2012; Knowles & Morris, 2014; The Electropedia, 2015) let each battery age individually, such that it is hard to predict a battery’s aging behavior.
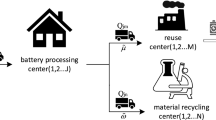
Even if removed from cars, repurposing the batteries for less demanding scenarios is a promising strategy (Cready et al, 2003; Narula et al, 2011; Ahmadi et al, 2017) to generate additional revenues and to reduce the total costs of electric vehicles (Elkind, 2014; Knowles & Morris, 2014). In stationary applications, the battery system is permanently installed, e.g., for storing energy in a smart home, as a buffer storage for wind parks, or for stabilizing off-grid systems (Patten et al, 2011; Knowles & Morris, 2014). In mobile applications, the battery propels devices with lower demands than cars, such as forklifts or wheelchairs.
Whereas early proof-of-concept projects have demonstrated that repurposing batteries is feasible from a technical point of view (Sachenbacher et al, 2012; Gohla-Neudecker et al, 2015), business models are only beginning to emerge (St. John, 2015). However, the market for used batteries will likely be intermediary-based (Klör et al, 2015a). Acting on behalf of a car manufacturer, the intermediary will collect, repurpose, and sell used batteries to second-life customers.
For three reasons, matching batteries and scenarios is a complex decision problem. First, each battery is unique regarding its electric properties, usage history, and condition. Second, the importance of technical properties varies greatly among scenarios; for instance, the weight of a battery is far more constraining in mobile than it is in stationary applications. Third, batteries can be repurposed en bloc, decomposed into their subsystems, or combined with other batteries.
Repurposing products as a class of decision problems
Implementing end-of-life strategies for products, such as remanufacturing, reuse, repurposing, and recycling, is motivated by producers’ environmental responsibility, environmental legislation, and economic considerations (Seitz, 2007). Previous research has discussed these strategies as product recovery management (Thierry et al, 1995), closed-loop supply chain management (Guide et al, 2003), or reverse logistics (Fleischmann et al, 1997). Recurring research topics include selecting optimal end-of-life strategies (Staikos & Rahimifard, 2007; Wadhwa et al, 2009), implementing reverse logistics for used products (Chouinard et al, 2005), and informing product recovery activities (Rahimifard et al, 2004). However, no research has been conducted on making decisions on repurposing complex and valuable products – such as electric vehicle batteries – and using them in second-life application scenarios.
In line with Simon (1977, p. 41), we conceptualize repurposing used products as a four-step decision-making process (Figure 1). First, in an intelligence phase, the properties of the available products and the requirements of the scenarios are explored. Second, in a design phase, a consideration set of scenarios in which each product can be repurposed is compiled based on assessing the fit (or misfit) between the products and scenarios in terms of specific decision criteria. Third, in a choice phase, the acceptable (“satisficing”) or the best (“maximizing”) (Simon, 1956) scenario for which to repurpose a product is selected by the decision-maker. In a maximizing strategy, this allocation is supposed to be optimal for the entire set of available products. Fourth, in an implementation phase, repurposing the products might necessitate additional activities to fit the battery to the scenario, such as adding technical components or value-added services that are needed to operate the battery.
The decision problem of matching objects from two sets classifies, in graph theory, as the bipartite matching problem (Schrijver, 2003) or, in operations research, as the assignment problem (Hillier & Lieberman, 2000; Anderson et al, 2009). This decision problem can be represented by bipartite graphs (Figure 2). Research on bipartite graphs and related matching problems has a long history (Plummer, 1992; Schrijver, 2003) and applies to several similar problem contexts, e.g., matching employees to jobs (Taha, 2010).
As every graph, a bipartite graph consists of vertices and edges. However, a bipartite graph separates its set of vertices in two disjoint partitions (bipartitions) (Diestel, 2000). Edges in a bipartite graph connect vertices from two bipartitions only (Figure 2, left). In the spirit of the bipartite matching problem, a matching in a bipartite graph is a subset of all edges containing only those edges that do not share one common vertex in each bipartition (Figure 2, right).
Businesses that repurpose used products need to identify optimal assignments between products and second-life scenarios. Such a matching is required for, e.g., incomplete and complete bipartite graphs since not every vertex from one set (e.g., product) is necessarily eligible for matching to all vertices of the other set (e.g., scenario). Hence, depending on the structure of a bipartite graph (e.g., regular and incomplete bipartite graph), it is possible to find a maximum cardinality matching (maximum matching hereafter) or even perfect matching in weighted (e.g., assignments with the best fit and/or best revenues) and unweighted (feasible assignments) bipartite graphs (Schrijver, 2003). Plenty of algorithms have been proposed for efficiently solving bipartite matching problems (Schrijver, 2003; Plummer, 1992). In addition, these problems can be formulated and solved using binary integer linear programming (Schrijver, 2003; Bondy & Murty, 2008; Vanderbei, 2008).
Decision support systems
Considering larger quantities in both sets of used products and second-life scenarios, the organizational task of manually identifying (all) feasible assignments or even a maximum matching might become cumbersome, expensive, and thus inoperable. Furthermore, it seems to be impossible to manually identify a weighted maximum matching that provides a global optimum (e.g., best technical fit and/or economic performance). Because such efficient solutions are required to run a business successfully, the need for information systems, such as decision support systems (DSSs), arises.
Depending on the specific decision problem, different types of DSSs apply (Power, 2004), each of which comprises a “dominant component driver” (p. 161). Since model-driven DSSs (Power & Sharda, 2007) contain quantitative and mathematical models (e.g., for binary integer linear programming) as their main component driver (Power, 2000, 2004), they can serve for modeling and solving bipartite matching problems to identify a maximum matching of used products and scenarios.
The generic architecture of such model-driven DSSs is comprised of three components (Keen, 1980; Sprague Jr., 1980; Sprague Jr. & Carlson, 1982; Sen & Biswas, 1985; Shim et al, 2002; Holsapple, 2008). Required data for decision-making are stored in the database management system. Decision models are specified in a model-base management system. Human decision-makers are guided through the decision processes and provided with functionalities to input and output decision-related data by user interfaces.
Research method
Repurposing batteries qualifies as a “heretofore unsolved and important business problem” (Hevner et al, 2004, p. 82) and warrants conducting a design science research project. Whereas the maturity of this application domain is low, the solution maturity of designing and solving optimization problems, i.e., assignment problems, is high. Therefore, we position our paper as exaptation research (Gregor & Hevner, 2013), an approach focused on adopting artifacts from one field to solve problems in another field.
In line with the dual mission of design science research to design applicable IT artifacts and to develop theories for design and action (March & Smith, 1995; Nunamaker Jr. & Chen, 1990; Walls et al, 1992; Hevner et al, 2004; Gregor & Jones, 2007), our objective was twofold. In terms of developing theories for design and action, we exapted concepts, methods, and tools from the fields of operations research, decision support systems, and decision science to design a class of DSSs that fosters decision-making for repurposing any kind of product. In terms of designing an applicable IT artifact, we instantiated this class of systems by developing a DSS for repurposing used batteries. The instantiation involved two steps. First, we conducted a Delphi study with battery experts to parameterize the generic decision models for the specific problem of repurposing batteries. Second, we surveyed a panel of battery experts to define which of the identified technical parameters have hard upper bounds and lower bounds. These bounds determine if assigning a battery to a scenario is feasible.
IT artifacts designed in DSR projects must be demonstrated and/or evaluated to assess their utility and applicability (Venable et al, 2016). While a demonstration serves to document the IT artifact’s ability “to solve one or more instances of the problem” (Peffers et al, 2008, p. 55), an evaluation documents “how well the IT artifact supports a solution to the problem” (Peffers et al, 2008, p. 56). To evaluate our design, we performed a field experiment, an approach often used for naturalistic evaluation in DSR (Venable et al, 2016). The field experiment revealed that the instantiated system improves the hit rate, miss rate, precision, fallout, and accuracy of decisions on repurposing used batteries. Other researchers can use a similar approach to design and evaluate their own DSSs for repurposing other types of products, thereby instantiating the proposed class of DSSs.
In terms of the nominal design science research methodology (Peffers et al, 2008), we summarize our research approach in Table 1.
Artifact description
This section provides an outline of the developed IT artifact in line with the three components of a model-driven DSS.
Data
The DSS’s database contains records that characterize all available products and scenarios such that used products and scenarios can be matched. Product records must include any technical properties that are relevant for solving the assignment problem. Scenarios must be described in terms of their lower bounds, target values, and upper bounds on these technical properties.
Data in the instantiated DSS for repurposing used batteries are stored in a relational database. Batteries are described based on a domain-specific modeling language (Klör et al, 2015b), including the battery’s master data (e.g., battery type, size, weight), usage history (e.g., cycles of (dis)charging, count of deep discharges taken), and condition (e.g., remaining capacity, voltage, amperage, internal resistance). Scenarios are described in terms of the (technical) requirements a battery to be used in this scenario must possess, including its capacity, voltage, and amperage. For each requirement of each scenario, the upper bound, target value, and lower bound can be stored in the database. This is important to account for the different requirements of mobile and stationary scenarios.
Decision models
We designed two decision models for matching batteries and scenarios (see their mathematical formulation in the “Appendix”). While the first decision model identifies all technical feasible assignments, the second decision model identifies a maximum matching regarding the minimal relative deviation of all decision parameters. Both models are stored in the DSS’s model-base as binary integer linear programs. They are solved at runtime by a mathematical optimization solver.
While the decision models support repurposing any product, as long as the decision task qualifies as a bipartite matching problem, the decision models need to be parameterized for repurposing any individual product. For instance, repurposing used batteries requires defining upper bounds and lower bounds for many technical parameters, which are subject to natural laws (e.g., Ohm’s law).
Decision model for identifying all feasible assignments
Although this decision model does not correspond to a bipartite matching problem at its heart, the model defines the decision-maker’s course of action for making manual assignments. For that to happen, the decision model maximizes the number of assignments and results in the set of all feasible assignments. To ensure technical feasibility, the decision model comprises two constraints representing upper bounds and lower bounds on the technical parameters (Table 2).
Decision model for identifying optimal assignments
Beyond compiling all feasible assignments, decision models are required to identify an (optimal) maximum matching of all products and all scenarios. Since scenarios specify minimum (lower bounds), ideal (target values), and maximum (upper bounds) requirements, products that meet these requirements best are reasonably the preferred choice. Therefore, we design a decision model that minimizes the relative deviation of all products’ parameters and all scenarios’ ideal parameters, identifying the most efficient matching set of all feasible assignments. In other words, the parameters of each product should match the requirements of the scenarios as closely as possible.
In addition to the feasibility constraints included in the first decision model, two constraints are added to ensure that one product is assigned to, at most, one scenario and that one scenario is assigned to, at most, one product. Regarding the objective for minimizing the relative deviation of the technical parameters, the solver would optimally make no assignments, since the zero vector would contribute best to the defined objective function. To find an optimal solution anyway, a constraint for identifying the maximum cardinality (k) of the bipartite matching problem is included in the decision model (Table 3).
For repurposing used batteries, we argue that the repurposing of as many batteries as possible identifies this maximum cardinality, since batteries suffer from calendar aging effects (Broussely et al, 2005; Barré et al, 2013) diminishing the batteries’ value over time. To quantify this maximum cardinality mathematically, an additional optimization problem of maximizing the number of assignments, subject to the same constraints applied in the minimization problem, is solved (Table 4).
The result of this optimization strategy identifies the weighted maximum matching with an optimal technical fit across all assignments.
User interface
Inspired by Simon’s (1977) decision-making process, the DSS’s user interface reflects the three steps of intelligence, design, and choice (Figure 3). In the intelligence phase, available products and scenarios (the decision objects) stored in the DSS’s database are selected and a check for inconsistencies in the decision objects’ data records is performed. If data required for instantiating the decision models are missing, three model adaptation strategies are available: (1) supplementing the incomplete decision objects by inserting any missing data; (2) removing decision objects with incomplete data from the decision-making process; (3) not solving inapplicable decision models. In the subsequent design phase, the decision models are instantiated. By solving the instantiated decision models, the choice phase supplies decision-makers with feasible and with optimal assignments.
We designed the user interface of our DSS for repurposing batteries (Figs. 4, 5, 6) to instantiate the generic decision process. Based on the available data on the selected batteries and scenarios, a model check component reveals whether the decision models are applicable. For instance, if some battery data are unavailable because of battery management system’s data encryption or insufficient data-recording strategies (Monhof et al, 2015), some decision models may not be applicable. Subsequently, the DSS solves the decision models to identify an optimal matching, indicated by the assignments highlighted in green color (Figure 6). The DSS contains a model-base management system (Figure 7) to enable users to design and modify the decision models based on any specific product and scenario properties that can result in different objectives and constraints.
Model parametrization, demonstration, and evaluation
Parameter elicitation
We elicited the parameters that govern the decision process in three steps. First, we performed a literature search on second-life application scenarios for batteries, resulting in a categorized list of parameters. Second, we performed a workshop with seven battery experts to complement the parameters and evaluate their correctness. Third, we performed a Delphi study to weight the relevance of the parameters for characterizing a stationary application scenario, in which the battery is used in a private household for optimizing the use of energy from an installed photovoltaic panel, the so-called residential load following (Prüggler, 2012). We invited 68 battery experts who deal with battery systems or the repurposing of batteries in their day-to-day business to evaluate 45 parameters in 11 categories and to add any missing parameters. A panel of 20 battery experts participated in the first round. In the spirit of a group decision-making process that is provided by a Delphi study (Linstone & Turoff, 1975; Okoli & Pawlowski, 2004), the results were aggregated and passed back to the panelists. Subsequently, we asked the panelists to weight the relevance of the parameters again. From the 20 participants of the first round, 15 also responded to the second round. Due to the high bounce rate and stable answers for most parameters, we concluded the study after two rounds (Figure 8). Based on the results, we compiled a set of parameters for describing second-life application scenarios for used batteries in our DSS.
Results of the Delphi study on parameter elicitation (round 1: n = 20; round 2: n = 15) (Beverungen et al., 2017).
Decision rules for technical feasibility
Based on the parameters elicited, we asked seven battery experts to identify constraining technical properties (upper bounds and lower bounds) that they considered important for stationary scenarios. Since only the parameters of the three categories of “adequacy,” “durability,” and “reliability” deal with technical requirements, parameters from the other categories were excluded from this expert survey, as were parameters that received less than half the number of the available votes. However, four exceptions were made regarding the technical parameters “required charging current” (included with 47% of the votes), “required discharging current” (included with 40% of the votes), “derating factor” (excluded with 80% of the votes), and “tolerable mean time to restoration” (excluded with 87% of the votes). The last two parameters were excluded because they cannot be measured properly. “Required charging current” and “required discharging current” were included since they received more than half the votes in the first Delphi round. The remaining fifteen technical parameters (Table 5) were presented to the panelists to identify exclusion criteria that guide the decision-making process (i.e., to exclude batteries that exceed or fall short of the bounded requirements in a scenario). Based on the experts’ majority view, we explored if a technical parameter \(({\text{TP}}_{i} )\) should be constrained by an upper and/or lower bound \((n_{i} \ge 4)\) or not \((n_{i} < 4)\).
Subsequently, we analyzed the data to derive decision rules that govern the fit or misfit of a battery vis-à-vis the technical requirements for applying used batteries to smart home scenarios.
Finding 1 Ten \({\text{TP}}_{i} \;\left( {i \in \left\{ {2,4,6,7,8,9,10,11,14,15} \right\}} \right)\) have neither an upper bound nor a lower bound. For instance, if a scenario requests a battery that should minimally serve 10 kWh, a particular battery that provides either 7 kWh or 17 kWh could be utilized in this scenario. These parameters are unconstrained because they affect the scenario’s economic perspective rather than its technical feasibility. A battery that fails to meet, for example, a scenario’s capacity requirement would either overachieve or underachieve the scenario’s needs without compromising the technical feasibility of repurposing the battery. Hence, these parameters do not require dedicated constraints in the decision models. However, since the experts in the Delphi study attested that most parameters have a raison d’être, these unconstrained parameters could still be included to the objective function of the technical decision model for minimizing the total relative technical deviation of batteries assigned to scenarios.
Finding 2 While the parameters identified in finding 1 remained unconstrained, the experts unanimously determined that the nominal voltage \(({\text{TP}}_{1} )\) in a scenario must be strictly met by the battery because each electric load requires a constrained range of voltage in which it can be operated. Following the European norm “EN 50160” (European Committee for Electrotechnical Standardization, 2011), a range of ca. ±10% of the “nominal voltage” requirement, which is defined for a scenario, is acceptable. Consequently, the decision model must be supplemented with two inequality constraints that define this corridor.
Finding 3 With regard to the technical feasibility of assignments, four parameters, \({\text{TP}}_{i}\; \left( {i \in \left\{ {3,5,12,13} \right\}} \right)\), have no upper bound, but all are constrained by a lower bound. For instance, the electric power requirement of a scenario must be fulfilled to run the scenario’s electric loads properly, but if the battery potentially provides more electric power than needed, it does not compromise the scenario’s technical feasibility. Therefore, lower bounds must be put on these parameters.
Finding 4 Linking the assessment data acquired by the Delphi study (importance of parameters for scenario characterization) to the assessment results from the expert survey (important decision rules regarding the technical feasibility of batteries in scenarios) reveals that parameter weights could be derived and introduced to the objective function in order to minimize the scenarios’ relative technical deviations. In this way, the objective function for minimizing the relative technical deviation of battery parameters to the lower bounds or target values of the respective scenario requirements can work more precisely since some parameters characterize the quality and value of a used battery better than others. However, since the weighting of the technical parameters requires further in-depth knowledge, which could be gained by technical investigations of the field of repurposed batteries in the future, the objective function is currently defined to weight every technical parameter.
Finding 5 Based on finding 4, the data point at a contradiction. While the experts from the Delphi study stated that \(T_{5}\) is less important than the other parameters are, the experts in the survey advocated that this parameter must be constrained by a lower bound. However, a constrained parameter cannot be irrelevant, since it seems to have a substantial influence on the technical feasibility of a battery.
Finding 5 in particular convinced us that a triangulation of the expert survey’s results is required. Therefore, we asked two additional battery experts to assess the appropriateness, quality, and coherence of the decision rules we derived. After the two independent experts agreed with the majority view regarding the parameters’ boundaries, we asked which parameters could be easily assessed and, thus, extracted from used battery systems to provide the decision models with suitable decision-related data. The experts found a consensus in six \({\text{TP}}_{i}\; \left( {i \in \left\{ {1,2,3,4,5,7} \right\}} \right)\) remaining from the initial set. Three \({\text{TP}}_{i}\; \left( {i \in \left\{ {2,4,7} \right\}} \right)\) are included, even though they have no hard upper or lower bounds, because they are easily measurable and the experts of the Delphi study considered them relevant to the optimal technical assignment.
Although lower bounds were identified for the power source’s “open circuit voltage” and “voltage at maximum power”, these parameters were excluded because they are not directly comparable to the batteries’ parameters. Other parameters identified in the Delphi study were found to be too vague to be considered in a decision rule. For instance, the parameter “tolerable mean uptime until first failure” deals with a statistical fact that is difficult to measure or determine up-front, and empirical field data on this item are still unavailable.
Field experiment
In order to demonstrate that the implemented DSS successfully matches batteries and scenarios, we defined two decision tasks. For both decision tasks, we generated four used batteries and four scenarios to populate the DSS’s database. Generating consistent test data on used batteries was necessary since data on a sufficiently large set of used batteries are not publicly available.
Informed by two previous studies, we conducted a field experiment to compare the decision quality reached by human agents who used our DSS with the decision quality reached by human decision-makers without using a DSS. While research reminds us that human decision-making is constrained by bounded rationality (Simon, 1977), we sought to quantify the increase in decision quality that can be attributed to using our DSS as an aid in a simplified decision process. In line with the demand to evaluate IT artifacts with “testable propositions or hypotheses” (Gregor & Jones, 2007, p. 317), the field experiment was focused on testing four propositions.
Proposition 1
The decision quality of human agents who identify all feasible assignments of a given set of used batteries and scenarios without using an IT artifact are inferior to that of agents who use our DSS.
Proposition 2
The decision quality of human agents who quantify the cardinality of the maximum matching of a given set of used batteries and scenarios without using an IT artifact are inferior to that of agents who use our DSS.
Proposition 3
The decision quality of human agents who identify the weighted maximum matching of a given set of used batteries and scenarios without using an IT artifact are inferior to that of agents who use our DSS.
Proposition 4
Human agents who must identify all feasible assignments, quantify the cardinality of the maximum matching, and identify the weighted maximum matching of a given set of used batteries and scenarios without using an IT artifact spend more time on decision-making than agents who use our DSS.
The field experiment was set up as follows. Data related to used batteries were generated by battery experts, who based their assumptions on existing batteries’ master data acquired from official battery specifications. Data related to second-life scenarios (smart home case) were compiled from available photovoltaic panels and mean energy requirements of households with varying numbers of residents and usage profiles. The scenarios in this case request a stationary energy storage solution for storing energy from photovoltaic panels (charging) and for providing electric power (discharging). The used battery instances and the scenarios’ requirements (Table 6) were defined in terms of the technical parameters identified as important in our Delphi study (Figure 8).
Subsequently, eight battery experts were provided with these decision objects in order to identify all feasible assignments and propose a maximum matching. Based on their self-assessment (Table 7), we dealt with experts having an advanced (ADV) and excellent (EXC) level of battery expertise in the four domains battery research (RES), battery manufacturing (MAN), battery pack development (BPD), and BMS development (BMSD).
First, the experts proposed assignments for matching each battery to each scenario in order to determine whether a single assignment is feasible. Since the field experiment focused on analyzing the experts’ independent decision quality, the experts were not provided with the decision rules that were compiled in our expert survey. The optimal solution of this case is numerically solved by the DSS to the total number of \(Z_{\text{opt}} = 10\) feasible assignments (cf. Table 8).
Then, based on these feasible assignments, the experts were asked to find a maximum matching. In the proposed case, the solution of this decision task referred to a perfect matching (\(Z_{\text{opt}} = 4\)), as every battery could uniquely be assigned to a scenario and vice versa. Experts were not asked to decide in line with a predefined objective function, but minimizing the sum of the technical parameters’ relative deviations would be the most reasonable and efficient decision strategy one could apply. Since the field experiment case’s total number of feasible assignments (\(k = 4\)) could be optimally realized, the efficient set (Table 8) contributed to the global minimum of the total parameters’ relative deviations (\(Z_{\text{opt}} = 41.25\)).
Binary classification was used in the process of analyzing the result sets that were derived by the battery experts. Hence, based on the computed DSS’s results, the count of true-positive (TP), true-negative (TN), false-positive (FP), and false-negative (FN) answers was determined from the experts’ assignments. Five metrics – “precision,” “recall” (hit rate), “false-negative rate” (miss rate), “fallout,” and “accuracy rate” – were computed to reveal the quality of the human agents’ decisions (e.g., Chinchor, 1991; Fawcett, 2006; Powers, 2011). Other measures are available for characterizing the performance of classifiers, such as the “\(F_{\beta }\) score” (based on the effectiveness measure of van Rijsbergen, 1979) and “Matthews correlation coefficient” (MCC) (Matthews, 1975).
A more sophisticated accuracy measure, the \(F_{\beta }\) score is a harmonic mean of precision and recall that indicates the respective metric’s β-induced importance, where \(\beta\) is usually defined for doubling the importance of precision (\(\beta = 0.5\)) or recall \((\beta = 2)\) or weighting both equally (\(\beta = 1\)) (Chinchor, 1991). Since batteries are dangerous goods, erroneous repurposing decisions could lead to undesirable effects in the respective scenarios. Therefore, we argue that precision is more important for repurposing used batteries than recall is, so we used the \(F_{0.5}\) score in the analyzing our field experiment.
The MCC is regarded as a strong measure since “[t]he correlation coefficient uses all four numbers (TP, TN, FP, FN) and may often provide a much more balanced evaluation of the prediction than, for instance, the percentages.” (Baldi et al, 2000, p. 415, italics in the text). By returning a continuous value in the interval of \(\left[ { - 1, + 1} \right]\), the coefficient indicates whether a prediction is imperfect (\(- 1\)), perfect (\(+ 1\)), or not better than random (\(0\)) (Matthews, 1975). Thus, the MCC “[…] immediately gives an indication [of] how much better a given prediction is than a random one.” (Matthews, 1975, p. 445)
Testing Proposition 1
The field experiment revealed that the battery experts made numerous mistakes in their decisions compared to all feasible assignments provided by the DSS’s decision model (cf. Table 8), which operates according to a majority view of seven battery experts. The aggregated results of the first decision task show the bounded rationality of human agents’ attempts to identify all feasible and infeasible assignments (Table 9).
No participant reached a flawless result in terms of the solution provided by the decision model for identifying all feasible assignments implemented in our DSS, although the experts performed with a respectable mean accuracy rate of 70.3%. However, this rate indicates that the experts did not identify, on average, 29.7% of the feasible assignments. While the decision quality of the independent participants 2 and 6 was equally good (e.g., high accuracy rate of 93.8% and \(F_{0.5}\) score of 97.8%, no FP decisions made, MCC of 0.878), participants 1 and 3 had poor to average results. For instance, the recall of participant 1 was low (20%), and participant 3’s decisions resulted in an intolerably high fallout rate (two-thirds).
Hence, the quality of the decisions made by manually finding all feasible solutions can be regarded as poor, confirming proposition 1, because used batteries were illegitimately assigned to scenarios (FPs of participants 3, 4, 5, 7, and 8). In addition, none of the participants found all feasible solutions (mean FN rate of 32.5%). Despite participants 1, 3, and 7’s comparably high accuracy rates (50%, 56.3%, and 56.3%) and \(F_{0.5}\) scores (55.6%, 64.8%, and 65.8%), the three participants performed randomly, as indicated by their respective MCCs (0.293, 0.035, and 0.163), which are close to zero.
Testing Propositions 2 and 3
With regard to both decision tasks of quantifying the maximum matching and identifying the weighted maximum matching (set of optimal assignments), the experts’ decision quality varied (Table 10). While participants 2, 3, 4, and 6 feasibly provided each scenario with only one battery (and vice versa), participants 1, 5, 7, and 8 did not find a feasible (technical constraint violations), correct (columns’ and rows’ sum greater than one), or perfect (\(k \ne 4\)) matching set. Since only four of the eight participants were able to quantify the maximum matching (k) comprising correct and feasible assignments, proposition 2 is confirmed. Additionally, since only participants 2, 4, and 6 identified the optimal solution (weighted maximum matching) and the other participants did not perform better than a random choice (indicated by the low MCC values), proposition 3 is confirmed, too. Moreover, it seems that participant 4 found the optimal set randomly (\({\text{MCC}} = 0.358\)). Even if the percentage difference between the solution proposed by participant 3 and the optimal set identified by the DSS is marginal (2.6%), we can expect that the difference would be larger in more complex and realistic sets that include many batteries and scenarios.
Testing Proposition 4
With respect to the required time for completing the decision tasks manually, the assignments that were created by the participants took considerably longer than those derived from the DSS (Table 11). Despite the small sample size, it took the participants an average of 12.4 min to complete all decision tasks. Since the DSS solves all requested tasks in milliseconds (0.016 s), proposition 4 is confirmed. While roughly twelve minutes is not an unreasonable time in which to make the requested decisions, a larger number of batteries and scenarios would likely result in a workload that could not be managed manually with good performance, whereas the DSS could deal with more complex decisions quickly.
Linking the time required for solving the decision tasks to the quality of the participants’ decisions does not clearly reveal a dependent variable. While experts 7 and 8 spent the shortest, respectively, longest timespan for completing the experiment, both participants had poor results in terms of their performance, as indicated by low recall (7), high fallout (both), and close to zero MCCs (both). As more field experiments are conducted, time will remain an influential variable affecting the decision quality since insufficient processing time and low decision quality are basic concepts that call for dedicated IT support, such as that provided by the DSS.
Discussion
In line with the dual mission of DSR, our findings contribute to descriptive and prescriptive knowledge (Mokyr, 2002; Gregor & Hevner, 2013).
First, we characterized repurposing used batteries to different scenarios as an important and yet unsolved decision problem that necessitates the design and development of a DSS. We showed that the underlying class of decision problems – assigning used physical products to scenarios – refers to a bipartite matching problem. Drawing from decision science literature, we explained how the decision process for repurposing used products, such as batteries, works.
Second, we adopted IT artifacts from the DSS and operations research fields designed to solve arbitrary bipartite matching problems. In the exaptation, we designed two decision models that (a) identify the technical fit between physical products and scenarios and (b) provide an optimal solution for matching many products to many scenarios. Subsequently, we designed a class of DSSs that supports the entire decision process, from modeling used products and scenarios to assigning used products to scenarios based on the decision models. The DSS offers support as it reliably prevents technical misfit between any product and any scenario. Moreover, it provides a (weighted) maximum matching of all products to all scenarios, based on technical fit. Other researchers can use the proposed class of systems as a blueprint for designing their own DSSs for repurposing physical products.
Third, we instantiated the designed class of DSSs for repurposing used batteries, based on parametrizing the decision models and implementing the DSS. Relying on natural laws, interviews, and a Delphi study with battery experts, we identified a set of fifteen technical parameters that constitute the technical fit between batteries and scenarios. These parameters detail the decision models, such that they identify all technical feasible assignments. We designed decision rules for each parameter to account for its upper bound and lower bound that govern the technical fit between a battery and a scenario. Evidence from our field experiment reveals that, even for the artificially small decision problem of assigning four batteries to four scenarios, our DSS leads to a decision quality that is considerably superior to the decisions reached by battery experts who do not use such a software. Among other benefits, using our DSS prevented the experts from matching batteries to non-fitting scenarios and enabled them to repurpose additional batteries, too. Using the software accelerated the decision process even in our small evaluation scenario. As regards realistically large decision scenarios comprising thousands of batteries and dozens of scenarios, a long tradition of DSS research illustrates that human decision-makers cannot identify an optimal solution due to the overwhelming mental workload (Paas & Van Merriënboer, 1994) and the bounded rationality that constrains human decision-making (Simon, 1977). Therefore, we assert that utilizing a DSS as designed in this paper is essential for successfully repurposing complex products, such as used electric vehicle batteries.
Conclusions
Against the backdrop of electric vehicles’ growing sales figures, repurposing used batteries is an economical, societal, and ecological imperative. On a more general level, a similar rationale applies to repurposing other valuable products in second-life application scenarios.
This paper presents the design, implementation, and evaluation of a class of DSSs that aid human decision-makers with matching used products, such as electric vehicle batteries, to scenarios. The system prevents a technical misfit between a product and a scenario and provides an optimal solution for matching many products to many scenarios. While even in an artificially small evaluation scenario our DSS increases the decision quality of repurposing batteries as opposed to manual decision-making, we argue utilizing a DSS is indispensable for repurposing batteries on an industrial scale. Since our DSS is the first system to aid decision-makers with repurposing used batteries, we propose a solution to a heretofore unresolved decision problem.
Other researchers can extend the proposed class of systems as well as the instantiated system’s functionality in various ways. Additional decision models can maximize the ecologic sustainability of used products, whereas maximizing business value necessitates adding parameters like costs, prices of rival products, and a customer’s willingness-to-pay to the decision models. As regards technical considerations, scenarios might be incompatible with repurposing exactly one product, such that the DSS needs to match scenarios with interconnected products or with a product’s sub-components. From the perspective of offering complete solutions, decision-makers might not only match products to scenarios, but may configure more complex value propositions that consist of products and value-added services. Thus, used products might be bundled with services to transport the product to the field, starting it up, and operating it to create value-in-use for customers. To provide the required functionality, the DSS will have to move beyond matching products and scenarios to afford configuring individual value propositions from a catalog of used products and value-added services. From the perspective of economic theory, the system will have to avoid the adverse selection effect of the market for used batteries as a lemon market, as suggested by lemon market theory (Akerlof, 1970), so as to establish and sustain a market for trading used products.
References
Ahmadi L, Fowler M, Young SB, Fraser RA, Gaffney B and Walker SB (2014) Energy efficiency of Li-ion battery packs re-used in stationary power applications. Sustainable Energy Technologies and Assessments 8, 9–17.
Ahmadi L, Young SB, Fowler M, Fraser RA and Achachlouei MA (2017) A cascaded life cycle: reuse of electric vehicle lithium-ion battery packs in energy storage systems. The International Journal of Life Cycle Assessment 22(1), 111–121.
Akerlof G (1970) The Market for ‘Lemons’: Quality uncertainty and the market mechanism. The Quarterly Journal of Economics, 87(3), 488–500.
Anderson DR, Sweeney DJ, Williams TA, Camm JD and Martin K (2009) An Introduction to Management Science: Quantitative Approaches to Decision Making (13th edition). South-Western Cengage Learning, Mason, Ohio, USA.
Baldi P, Brunak S, Chauvin Y, Andersen CA and Nielsen H (2000) Assessing the accuracy of prediction algorithms for classification: an overview. Bioinformatics 16(5), 412–424.
Barré A, Deguilhem B, Grolleau S, Gérard M, Suard F and Riu D (2013) A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. Journal of Power Sources 241, 680–689.
Beer S, Gómez T, Dallinger D, Momber I, Marnay C, Stadler M and Lai J (2012) An economic analysis of used electric vehicle batteries integrated into commercial building microgrids. IEEE Transactions on Smart Grid 3(1), 517–525.
Beverungen D, Bräuer S, Plenter F, Klör B and Monhof M (2017) Ensembles of context and form for repurposing electric vehicle batteries: an exploratory study. Computer Science - Research and Development 32(1), 195–209.
Bondy JA and Murty USR (2008) Graph Theory. Springer. Berlin, Heidelberg, Germany.
Broussely M, Biensan P, Bonhomme F, Blanchard P, Herreyre S, Nechev K and Staniewicz RJ (2005) Main aging mechanisms in Li ion batteries. Journal of Power Sources 146, 90–96.
Burke AF (2009) Performance, Charging, and Second-use Considerations for Lithium Batteries for Plug-in Electric Vehicles. Technical Report. Institute of Transportation Studies, University of California, Davis, California, USA.
Chinchor N (1991) MUC-3 evaluation metrics. In: Proceedings of the 3rd Conference on Message Understanding—MUC3’91, pp 22–29.
Chouinard M, D’amours S and Aït-kadi D (2005) Integration of reverse logistics activities within a supply chain information system. Computers in Industry 56(1), 105–124.
Cready E, Lippert J, Pihl J, Weinstock I and Symons P (2003) Technical and Economic Feasibility of Applying Used EV Batteries in Stationary Applications. Technical Report. Sandia National Laboratories, Albuquerque, New Mexico, USA.
Diestel R (2000) Graph Theory (2nd edition). Springer, New York, New York, USA.
Ebner M, Marone F, Stampanoni M and Wood V (2013) Visualization and Quantification of Electrochemical and Mechanical Degradation in Li Ion Batteries. Science 342(6159), 716–720.
Elkind EN (2014) Reuse and Repower—How to Save Money and Clean the Grid with Second-Life Electric Vehicle Batteries. Technical Report, UCLA School of Law, Los Angeles, California, USA.
EUROPEAN COMMITTEE FOR ELECTROTECHNICAL STANDARDIZATION (2011) EN 50160: Voltage characteristics of electricity supplied by public distribution systems.
EVWORLD.COM INC (2011) Lithium Battery Recycling Expected to Reach $2B By 2022. [Online] http://evworld.com/news.cfm?newsid=25315 (accessed 21/04/15).
Fawcett T (2006) An introduction to ROC analysis. Pattern Recognition Letters 27(8), 861–874.
Fleischmann M, Bloemhof-ruwaard JM, Dekker R, Van der laan E, Van nunen JA and Van wassenhove LN (1997) Quantitative models for reverse logistics: A review. European Journal of Operational Research 103(1), 1–17.
Gohla-neudecker B, Bowler M and Mohr S (2015) Battery 2nd life: leveraging the sustainability potential of EVs and renewable energy grid integration. In: Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), pp 311–318.
Gregor S and Hevner AR (2013) Positioning and presenting design science research for maximum impact. MIS Quarterly 37(2), 337–356.
Gregor S and Jones D (2007) The anatomy of a design theory. Journal of the Association for Information Systems 8(5), 312–335.
Guide V, Harrison T and Wassenhove L Van (2003) The challenge of closed-loop supply chains. Interfaces 33(6), 3–6.
Hevner AR, March ST, Park J and Ram S (2004) Design science in information systems research. MIS Quarterly 28(1), 75–105.
Hillier FS and Lieberman GJ (2000) Introduction to Operations Research (7th edition). McGraw-Hill Higher Education, New York, New York, USA.
Holsapple CW (2008) DSS architecture and types. In: Handbook on Decision Support Systems 1: Basic Themes, pp 163–190. Springer: Berlin, Heidelberg, Germany.
Howard B (2013) GM Turns Your Old Chevy Volt Battery Into a Whole-House UPS|ExtremeTech. [Online] http://www.extremetech.com/extreme/155589-gm-turns-your-old-chevy-volt-battery-into-a-whole-house-ups (accessed 21/04/15).
Keen PGW (1980) Adaptive design for decision support systems. ACM SIGOA Newsletter 1(4–5), 15–25.
Klör B, Beverungen D, Bräuer S, Plenter F and Monhof M (2015) A market for trading used electric vehicle batteries—theoretical foundations and informations systems. In Proceedings of the Twenty-Third European Conference on Information Systems (ECIS 2015). Münster, pp 1–18.
Klör B, Bräuer S, Beverungen D and Monhof M (2015) A domain-specific modeling language for electric vehicle batteries. In Proceedings of the International Conference on Wirtschaftsinformatik 2015. Osnabrück, pp 1038–1054.
Knowles M and Morris A (2014) Impact of second life electric vehicle batteries on the viability of renewable energy sources. British Journal of Applied Science and Technology 4(1), 152–167.
Lache R, Nolan P and Crane J (2008) Electric Cars: Plugged In Batteries must be included. Deutsche Bank, FITT Research Report.
Linstone HA and Turoff M (1975) The Delphi Method—Techniques and Applications. Addison-Wesley, Reading, Massachusetts, USA.
March ST and Smith GF (1995) Design and natural science research on information technology. Decision Support Systems 15(4), 251–266.
Matthews BW (1975) Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochimica et Biophysica Acta 405(2), 442–451.
Mokyr J (2002) The Gifts of Athena: Historical Origins of the Knowledge Economy (5th edition). Princeton University Press, Princeton, New Jersey, USA.
Monhof M, Beverungen D, Klör B and Bräuer S (2015) Extending battery management systems for making informed decisions on battery reuse. In New Horizons in Design Science: Broadening the Research Agenda (Donnellan B, Helfert M, Kenneally J, VanderMeer D, Rothenberger M and Winter R, Eds), pp 447–454, Springer International Publishing, Dublin, Ireland.
Narula CK, Martinez R, Onar O, Starke MR, Andrews G and LABORATORY ORN (2011) Final Report—Economic Analysis of Deploying Used Batteries in Power Systems. Oak Ridge, Tennessee, USA.
Nunamaker JR. JF and Chen M (1990) Systems development in information systems research. Twenty-Third Annual Hawaii International Conference on System Sciences iii(3), 89–106.
Nykvist B and Nilsson M (2015) Rapidly falling costs of battery packs for electric vehicles. Nature Climate Change 5(4), 329–332.
Okoli C and Pawlowski SD (2004) The Delphi method as a research tool: an example, design considerations and applications. Information & Management 42(1), 15–29.
Paas FGWC and Van Merriënboer JJG (1994) Instructional control of cognitive load in the training of complex cognitive tasks. Educational Psychology Review 6(4), 351–371.
Patten J, Christensen N, Nola G and Srivastava S (2011) Electric vehicle battery—wind storage system. In: 2011 IEEE Vehicle Power and Propulsion Conference, VPPC 2011, pp 1–3.
Peffers K, Tuunanen T, Rothenberger MA and Chatterjee S (2008) A design science research methodology for information systems research. Journal of Management Information Systems 24(3), 45–77.
Pillot C (2012) The worldwide battery market 2011-2025. [Online] http://www.kigeit.org.pl/FTP/PRCIP/Literatura/063_The_worldwide_battery_market_2011_2025.pdf (accessed 21/04/15).
Plummer MD (1992) Matching theory—a sampler: from Dénes König to the present. Discrete Mathematics 100, 177–219.
Power DJ (2000) Web-based and model-driven decision support systems: concepts and issues. In: AMCIS 2000 Proceedings. Paper 387, pp 352–355.
Power DJ (2004) Specifying an expanded framework for classifying and describing decision support systems. Communications of the Association for Information Systems Volume (CAIS) 13(Article 13), 158–166.
Power DJ and Sharda R (2007) Model-driven decision support systems: concepts and research directions. Decision Support Systems 43(3), 1044–1061.
Powers DMW (2011) Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. Journal of Machine Learning Technologies 2(1), 37–63.
Price B, Dietz E and Richardson J (2012) Life cycle costs of electric and hybrid electric vehicle batteries and End-of-Life uses. In: IEEE International Conference on Electro Information Technology, pp 1–7.
Prnewswire (2014) Second-life batteries: from PEVs to stationary applications. [Online] http://www.prnewswire.com/news-releases/second-life-batteries-from-pevs-to-stationary-applications-242205851.html (accessed 21/04/15).
Prüggler W (2012) The impact of second life applications of electric vehicle batteries on customer’s mobility cost. In: Proceedings of the 12th Symposium Energieinnovation—Alternativen für die Energiezukunft Europas.
Rahimifard A, Newman ST and Rahimifard S (2004) A web-based information system to support end-of-life product recovery. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture 218(9), 1047–1057.
Van rijsbergen CJ (1979) Information Retrieval (2nd edition). Butterworth-Heinemann Ltd, Newton, MA, USA.
Sachenbacher M, Mayer T, Leucker M, Brand M and Jossen A (2012) Towards 2nd-Life Application of Lithium-Ion Batteries for Stationary Energy Storage in Photovoltaic Systems. In Proceedings of the ‘International Conference on Solar Energy for MENA Region (INCOSOL)’, pp 22–23, Amman, Jordan.
Sasaki T, Ukyo Y and Novák P (2013) Memory effect in a lithium-ion battery. Nature Materials 12(6), 569–575.
Schlick T, Hertel G, Hagemann B and Maiser E (2011) Zukunftsfeld Elektromobilität—Chancen und Herausforderungen für den deutschen Maschinen- und Anlagenbau. Technical Report, Roland Berger Strategy Consultants.
Schrijver A (2003) Combinatorial Optimization—Polyhedra and Efficiency (1st edition). Springer, Berlin, Heidelberg, Germany.
Seitz MA (2007) A critical assessment of motives for product recovery: the case of engine remanufacturing. Journal of Cleaner Production 15(11–12), 1147–1157.
Sen A and Biswas G (1985) Decision support systems: An expert systems approach. Decision Support Systems 1(3), 197–204.
Shahan Z (2014) The Electric Car Revolution - Why Electric Cars are Likely to Dominate in the Next Decade. [Online] http://www.fix.com/blog/why-buy-electric-cars/ (accessed 21/04/15).
Shim JP, Warkentin M, Courtney JF, Power DJ, Sharda R and Carlsson C (2002) Past, present, and future of decision support technology. Decision Support Systems 33(2), 111–126.
Simon HA (1956) Rational choice and the structure of the environment. Psychological Review 63(2), 129–138.
Simon HA (1977) The New Science of Management Decision. Prentice Hall, Englewood Cliffs, New Jersey, USA.
Sprague Jr. RH (1980) A framework for the development of decision support systems. MIS Quarterly 4(4), 1–26.
Sprague Jr. RH and Carlson ED (1982) Building Effective Decision Support Systems. Prentice Hall Professional Technical Reference.
Staikos T and Rahimifard S (2007) An end-of-life decision support tool for product recovery considerations in the footwear industry. International Journal of Computer Integrated Manufacturing 20(6), 602–615.
St. john J (2015) Nissan, Green Charge Networks Turn Second-Life EV Batteries Into Grid Storage Business|Greentech Media. [Online] http://www.greentechmedia.com/articles/read/nissan-green-charge-networks-turn-second-life-ev-batteries-into-grid-storag (accessed 25/02/16).
Taha HA (2010) Operations Research: An Introduction (9th edition). Prentice Hall, Upper Saddle River, New Jersey, USA.
THE Electropedia (2015) Battery Life (and Death). [Online] http://www.mpoweruk.com/life.htm (accessed 27/04/15).
Thierry M, Salomon M, VAN Nunen J and VAN Wassenhove L (1995) Strategic issues in product recovery management. California Management Review 37(2), 114–135.
Vanderbei RJ (2008) Linear Programming—Foundations and Extensions (3rd edition). Springer, Berlin, Heidelberg, Germany.
Venable J, Pries-heje J and Baskerville R (2016) FEDS: a framework for evaluation in design science research. European Journal of Information Systems 25(1), 77–89.
Waag W, Käbitz S and Sauer DU (2013) Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Applied Energy 102, 885–897.
Wadhwa S, Madaan J and Chan FTS (2009) Flexible decision modeling of reverse logistics system: a value adding MCDM approach for alternative selection. Robotics and Computer-Integrated Manufacturing 25(2), 460–469.
Walls JG, Widmeyer GR and EL Sawy OA (1992) Building an information system design theory for vigilant EIS. Information Systems Research 3(1), 36–59.
Author information
Authors and Affiliations
Corresponding author
Additional information
Accepting Editor: Ken Peffers.
Guest Editors: Bjoern Niehaves and Tuure Tuunanen.
The online version of this article is available Open Access.
Appendices
Appendix
- ADV:
-
Advanced
- BMSD:
-
Battery management system development
- BPD:
-
Battery pack development
- DSR:
-
Design science research
- DSS:
-
Decision support system
- EXC:
-
Excellent
- FN:
-
False negative
- FP:
-
False positive
- IT:
-
Information technology
- MCC:
-
Matthew’s correlation coefficient
- STP i :
-
i-th study participant
- RES:
-
Battery research
- TP i :
-
i-th technical parameter
- TN:
-
True negative
- TP:
-
True positive
- Z opt :
-
Optimal value of an objective function
Decision models
Nomenclature
Designators
Decision variables (model-endogenous)
Parameters (model-exogenous)
Technical decision model for identifying all feasible assignments
subject to
Technical decision model for identifying optimal assignments
subject to
where
subject to
Rights and permissions
Open Access This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/.
About this article
Cite this article
Klör, B., Monhof, M., Beverungen, D. et al. Design and evaluation of a model-driven decision support system for repurposing electric vehicle batteries. Eur J Inf Syst (2017). https://doi.org/10.1057/s41303-017-0044-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41303-017-0044-3