Does more competition result in better port performance?

Abstract

This study examines the impact of competitive pressure on port performance. We merge the competitive rivalry literature with the port management literature to explain the inverted U-shaped relationship between competitive pressure and port performance within the increasingly competitive realm of world ports. A newly designed index measures competitive pressure that organizations face based on market commonality and domain overlap. Using data for global hubs and national gateway ports, we find potential diseconomies of excessive competitive pressure on port performance.

Introduction

Over the past decade, various technological and regulatory changes have created unstable, contested business landscapes in the port sector. To effectively compete in global logistics and supply chains, ports now must adopt effective strategies and operations, contingent upon rapid change in their environment. Researchers are thus interested in inter-port competition in the maritime logistics sector. From an industrial economics perspective, the more competitive pressure a firm faces, the greater its performance (Kahn 1988). The empirical facts within the maritime logistics field, however, have not yielded clear evidence about the expected relationship between competition and performance (Cullinane et al. 2002). The complex relationship between port competition and performance originates from various market changes over the last decades in terms of trade liberalization and diversification of shipping routes, influences from port hinterlands, port strategies and management practices, and institutional capacity to implement new cost-recovery pricing schemes (Haralambides 2002).

In line with this thought, we argue that port competition is a multifaceted concept; complexity exists in the sense that ports are subject to national competition policies, and at the same time, influenced by geographical hinterlands in which neighbouring ports compete to gain market dominance. In this context, this study investigates the impact of competitive pressure on port performance, and makes the following major contributions. First, in conceptualizing the competitive environments that port organizations face, we differentiate between macro-level institutional competitive pressure (e.g. national competition policy) and organization-specific competitive pressure. Much business/logistics management literature, with the exception of competitive rivalry research, has focussed on competition at the industry level (Ang 2008; Baum and Korn 1996). Focussing on the competitive rivalry and port management literature, this study examines how ports face differing levels of competitive pressure (i.e. port-specific competitive pressure; henceforth ‘PSCP’), and how that pressure, in addition to macro-level competition institutions, influences port performance.

Our hypothesis and empirical findings suggest an inverted U-shaped relationship between the degree of competitive pressure ports face and their performance. Although previous studies have presumed a positive link between competition and performance, extreme competitive pressure from overlapping hinterlands (also called ‘market domains’ in Baum and Korn 1996; Chen 1996) may hinder ports’ long-term investment and strategic planning capabilities, in coordination with port supply chain actors, thus reducing port performance.

Second, the measure for competitive pressure proposed in this paper is based on the idea that port organizations face competitive tension from competitors that share hinterlands; the degree of impact is shaped by differences in competitor strengths, and therefore depends on ports’ geographic positions vis-à-vis their competitors, particularly their access to local/global markets and competitors (Barnett 1997). Our measure for estimating port competition intensity may thus apply to other sectors in which market domain-based or geographic location-driven competition is evident.

While the management aspect of port operations is an important part of port competition, the location of ports and their hinterlands are intrinsically geographically bound, and thus play an integral role in shaping the port competition–performance link by limiting market entry/exit. Looking into 138 of the world’s largest ports, we explore the relationships between competitive pressure and port performance.

Theoretical/empirical background

Competitive pressure was originally conceptualized as reflecting environmental aspects at the industry level: for example, market structure (Bain 1959). Organizational ecologists also initially adopted this structural view, recognizing that competition occurs between anonymous firms that can freely enter/exit markets while striving for limited resource pools.

Numerous studies have examined how firms under high competitive pressure improve their performance. Table 1 presents a list of representative theories and findings. We find that competitive pressure has a positive influence on organizational performance, although the impact on profitability and market share is more complicated (e.g. Ferrier et al. 1999).

Table 1 Mechanisms related to the impact of competition on performance

Most studies have assumed that competitive pressure stems from macro-level environmental factors: market structure or market-governing institutions (e.g. national-level competition policies). In this study, we distinguish organization-specific competitive pressure from macro-level institutional competitive pressure to better conceptualize the competitive environments that ports face and to understand ports’ competition–performance links.

Organizational competition

Firm-specific features shape the relational nature of competition and rivalry among firms (Barnet 1997). The idea is that the competitive pressure firms face is heterogeneous due to various conditions that affect firms’ capabilities and market contexts. Firms’ attributes—size, experience, resources, and their abilities to increase barriers to entry and imitation—affect their competitive intensity and their competitors’ chances of survival (Demsetz 1997). Varied market characteristics and different firms’ domains simultaneously create differentials in the competitive pressure that firms face.

Market commonality and functional similarity

The key components of organization-specific competitive pressure are market commonality (Chen 1996) and functional similarity (Kotler 2000). Market commonality refers to the extent of market overlap with competitors across various dimensions, such as product, geography, and brand. As the degree of overlap between focal firms’ market domains and other firms’ market domains increases (Baum and Korn 1996), the intensity of competition that focal firms face also increases (Scherer and Ross 1990). Functional similarity refers to the extent to which firms’ products and capabilities satisfy the same customer needs/performance expectations. Firms can thus identify strong competitors based on how well their rivals’ products/capabilities satisfy customer needs.

Firms essentially encounter distinctive rivals and shared markets with scarce customers and resources, depending on the particular market domain they target. Competitive intensity among multiple organizations is thus not symmetrically changed between competitors (Chen 1996), but is a function of each organization’s network position in the organizational population (Barnett 1997).

Port competitive pressure and hinterland markets

Inter-port competition in the port sector

The global port industry experienced significant shifts in the business landscape and market competition during the 1990s. Starting in the late 1980s and early 1990s, port sectors in various Western economies implemented several institutional reforms, including deregulation and decentralization. More recently, ports in Asia, Latin America, and the Middle East have also implemented reforms, seen also in Chinese ports in the early 2000s. These reforms, along with new technological developments, have lowered entry barriers for new port operators and investors, thus increasing uncertainty in port business environments. The liberalization of port services, trade openness, infrastructure investments, and new ‘pricing disciplines’ led many ports in the world to compete directly in order to capture newly emerging markets (Haralambides 2002, 2015). The traditional boundaries of port hinterlands have broadened and often overlap with those of other ports; globalized port competition beyond national boundaries thus emerged (Cullinane et al. 2005).

Hinterland markets as geographic market domains

The literature asserts that the key standard for defining inter-port competitive pressure is how much functionally similar ports serve the same or overlapping hinterland markets (Cullinane et al. 2005). Port hinterlands are “the market area[s] served by a port and from which a port draws its cargo” (UNESCAP 2005, p. 14); they are based on port access and patterns of customer patronage. Some port hinterlands extend across many nation states, while others remain within a single region. Market hinterlands differ from institutional and legal boundaries; hinterlands continuously expand or shrink as the key conditions facing ports change. Ports that are similar in function and resource usage thus normally compete, given the extent to which they share overlapping hinterland markets. Variances in the competitive pressure organizations face may widen as business environments become unstable (Chen et al. 2010).

Hypothesis

A shift in port business landscapes and escalating environmental selection due to global competition requires ports to delineate aggressive strategies and actions in order to avoid rivals’ threats and to shed operational inefficiency. Ports have strong incentives to reduce operational costs and adopt innovative cargo-handling technologies when they face high competitive pressure. The major intent of the proliferating alliances (Cass 1996) between major world ports and terminal operators (and between ports and shipping lines) is to find cost-effective ways to develop facilities to accommodate the ever-increasing ship sizes and intermodal transportation networks. Ports that face much competitive pressure attempt to design managerial structures that can reduce inefficient bureaucracy to reduce costs (Vickers and Yarrow 1988). For example, many world ports have adopted a ‘yardstick competition’ concept by comparing crane efficiency and cargo damage rates (Estache et al. 2002).

Nonetheless, there is the chance that a group of ports may face competitive pressure above a certain threshold from multiple head-to-head rivals and market volatility in a shared regional market. If ports face excessive degrees of competitive pressure, the industry recipe (Koka et al. 2006) that the ports have exercised loses validity. Ports should hasten to maintain consecutive temporary advantages under this hypercompetitive environment (Chen et al. 2010; D’Aveni 1994). Temporary advantage occurs, for instance, when ports build strategic alliances with leading global terminal operators, e.g. Hutchison Port Holdings (HPH), but when neighbouring ports also build alliances with the same or similar operators, the advantage of the focal ports erodes rapidly.

Ports can incur high transitory costs under excessive instability due to certain industrial characteristics, including long-term capital-intensive production, construction delays (Delmas and Tokat 2005), and spatially dispersed hinterland network infrastructure, all of which require strong strategic capital planning capabilities and risky new investments, without the benefits of instantly increased market share. Organizations that face excessive competitive pressure are disadvantaged for pursuing long-term planning and investment for innovation (Howitt 2004), as they must quickly respond to their rivals. Ports face increasing needs for strategic coordination between short-term operational efficiency and long-term collaboration among multiple port supply chain actors to promote hinterland infrastructure investment. Excessive competitive pressure potentially induces port organizations to focus on local competitors (Hoopes 2003) and shipowner’s short-term interests (e.g. minimizing ship turnaround times), and reduces attention to the long-term perspective and strategic collaboration (Ang 2008).

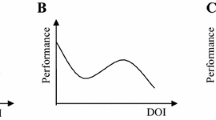
The aforementioned arguments suggest that an increase in PSCP would initially boost port performance, but ports that face competitive pressure above a certain threshold tend to display deteriorated performance (See Fig. 1). We thus hypothesize the following:

H1

An inverted U-shaped relationship exists between PSCP and port performance for certain periods of time.

Fig. 1

Proposed relationship between port competition and performance

We posit that this relationship is a relatively recent phenomenon. Before the early 1990s, monopolies in regional port markets were tolerated, based on natural monopoly arguments prevailing in ports and hinterland infrastructure. This mechanism allowed ports to face relatively low financial risks; they could set prices to cover their costs, and the demand for port services was relatively predictable (Clark et al. 2004). Even if ports did face some competitive pressure, the relatively predictable and benign business landscape was forgiving of their lack of capabilities for adopting proactive strategies (Ramaswamy 2001); the landscape endorsed competitive inertia and ‘comfortable inefficiency’ (Foster 1992). Thus, variations in competitive pressures (which all organizations feel) generated limited incentive effects on port performance. Following this line of thought, our proposal for an inverted U-shaped relationship between PSCP and performance is effective only for recent periods—for example, the post-2000s.

Methods

Scope of analysis

For our analysis of the port competition–performance link, we focussed on large-scale, global hubs, or national gateway ports, in 2004. Before the US housing market began to decline in 2006, leading to the global economic meltdown two years later, the selected year was the most dynamic for global shipping (annual growth of 14.4% in world container port traffic [World Bank 2015]), and it was thus suitable for testing our inverted-U hypothesis.

We have also added an analysis of the year 1991, as a contrast group against the year 2004. The global port sector experienced vast technological/institutional restructuring between these two periods, which caused greater market instability (Cheon et al. 2010). Comparing these two periods—which represent varying levels of environmental stability in the global container port market—provides us with a clearer picture for examining our hypothesis.

The idea of size-localized competition suggests that organizations in different size groups face fundamentally different mechanisms (e.g. minor fishing ports usually do not compete against major container ports), and that competition influences survival and performance (Hannan and Freeman 1989). Since economies of scale prevail in the port sector (Turner et al. 2004), smaller ports may face significant disadvantages in competition. We thus focussed on large-scale, global hubs or national gateway ports (Cheon et al. 2010) for constructing the comparison set of functionally similar organizations (138 world ports in 2004 and 98 ports in 1991).

Measuring PSCP

Measurement

Equation (1) presents the proposed measure of competitive pressure, hereafter called ‘hinterland market accessibility’ (HMA) (Cheon et al. 2008). HMA captures the extent to which the impact of each port reaches hinterland markets, discounted by any competitive threats that competing ports generate. Because the index measures the degree to which market demands support a port, given multiple competitors, the HMA of a port is inversely related to the intensity of competition:

$$\mathop {HMA_{i} }\limits_{i \ne k} = {{\sum\limits_{J} {\left( {GDP/D_{i,J}^{\alpha } } \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{J} {\left( {GDP/D_{i,J}^{\alpha } } \right)} } {\sum\limits_{J} {\sum\limits_{k = 1}^{m} {\left( {Q_{k} /D_{k,J}^{\alpha } } \right)} } }}} \right. \kern-0pt} {\sum\limits_{J} {\sum\limits_{k = 1}^{m} {\left( {Q_{k} /D_{k,J}^{\alpha } } \right)} } }},$$

(1)

where GDP _J is the gross domestic product of economic zone J (J = 1,2,…, N); D _i,J is the distance between port i (i = 1, 2,…, m) and economic zone J; D _k,J is the distance between port k and economic zone J; Q _k is the total throughput of port k $(k \ne i)$; and a is the distance impedance parameter.

In Fig. 2, since the hinterland markets related to port i consist of multiple, often legally defined economic zones, J _1, J _2, J _3,…J _N,, such as countries, states, and cities, the total market opportunities faced by port i are the additive aggregation of the hinterland market opportunities generated from the economic zones. The hinterland market opportunities can thus be expressed as a gravity model: $\sum\nolimits_{j} {\left( {GDP_{J} /D_{{i,J}}^{\alpha } } \right)}$, in which α is the distance impedance parameter. Let this scale value be a unique value for hinterland size of port i: i.e. port i’s unique geographic market domain, determined by the distinctive location of each port and the economic zones that are universally available to all ports.

Fig. 2

Conceptual diagram of hinterland market accessibility

The numerator of Eq. (1), hinterland size, should be discounted by the degree of threat from competing ports serving the overlapping hinterlands. The denominator of Eq. (1) assesses the port-specific degree of aggregated threats from all other ports across the economic zones considered. The aggregated threats of port i arise from (i) the aggregated size (and number) of competing ports, k, $\sum\nolimits_{{k = 1}}^{m} {Q_{k} }$ and (ii) the distance of each competitor, k, from the hinterland economic zones, J $\left( {\sum\nolimits_{k = 1}^{m} {1/D_{k,J}^{\alpha } } } \right)$. HMA essentially reflects the concepts of market domain overlap, market commonality rivals in a spatial dimension, and mass dependence competition (Barnett and Amburgey 1990).

Operationalization

The first issue when operationalizing HMA is to consider variations in demand across multiple economic zones. We apply two alternative approaches in order to compare the results and check the measures’ validity. The first, which is simpler and less data-intensive, uses countries’ economic data. We apply GDP data for calculating the aggregated sizes of the economic hinterlands for each port, and we use capital city locations (usually found in major economic conurbations) for measuring the distance between ports and the economic zones. We call this the HMA-Capitals model. While the assumption behind this is that capital cities are where major economic activities occur, this could be a source of error for larger countries’ economic activities. We adopt a second, more data-intensive approach to partly resolve this problem, using all global cities larger than 500,000 people. We name this the HMA-Cities model. We then assign each country’s GDP, using the ratio of city populations, based on the formula: $GDP_{j} = GDP_{c} \left( {P_{j} /\sum\nolimits_{l = 1}^{m} {P_{l} } } \right),$ where GDP _j  is the GDP assigned to city j; GDP _c  the GDP of country c, with which city j is territorially affiliated; P _j  the population of city j; and P _l= is the population of all cities within country c with >500,000 people.

The number of countries and cities considered for the 1991 and 2004 GDP data was 186 and 776, respectively, including most countries except small island ones. To calculate HMA, we initially consider the 257 largest container ports, which produced more than 90% of the 245 million 20-foot equivalent units (TEUs) handled by 533 container ports in the world in 2004 (CI 2004). The idea of scale-based selection suggests that smaller organizations will follow different mechanisms to deal with competitive pressure from scale gaps (Dobrev and Carroll 2003). We have thus removed the smallest ports (which produce the remaining 10% of world TEUs) for building our initial set of port samples engaged in competition.

We have measured distances along the geodesic curve using ArcGIS. The distance parameter α also had to be defined. The shape of the distance parameter can largely depend on the extent to which competition is local or global in a space dimension (Vogel 2008). In the case of local competition (high α), a port competes only with its direct neighbours, which is similar to the dyadic view of competition (e.g. Baum and Korn 1999). Under global competition (low α), a port competes with all other ports in the global port industry. This is also the approach early organizational ecologists have employed.

The level of α may also change depending on other distance-related factors which affect the spatial immobility of cargo movement between ports and economic zones. These include higher fuel prices in world oil markets, creating a high α. However, since few empirical studies have been conducted on the spatial scope of port competition, we also adopt a series of sensitivity analyses, attempting to avoid choosing between two extreme cases (global vs. local). We test a variety of cases with α values between 0.1 and 10 to confirm the consistency of data patterns with different scales of distance parameters, and to validate whether the results are consistent for certain ranges of distance parameters.

Variables for institutional competitive pressure

Because we differentiate between organization-specific competitive pressure and macro-level institutional competitive pressure, we have also collected data on several variables for the national-level institutional environment. For example, previous literature has discussed special restrictions on domestic participation of foreign suppliers of cargo-handling services, and how compulsory some port services are for incoming ships (Fink et al. 2002). Since limited information is available on these regulations, we have collected data on six variables for proxying national institutional environments: (1) number of administrative procedures for warehouse-building; (2) days needed to complete procedures for warehouse-building (from the World Bank [2005]); (3) customs procedures burden; (4) trade barriers prevalence; (5) government regulation burdens; and (6) national-level competition intensity in most industries (from the Global Competitiveness Reports [GCRs]; Schwab and Porter 2008).

Measuring port performance

We adopt data envelopment analysis (DEA) for measuring port performance. DEA translates Pareto efficiency into the relative efficiency of decision-making units (DMUs) based on non-parametric mathematical programming (Charnes et al. 1978). We have adopted the output-oriented DEA-CCR and DEA-BCC models, formalized in Eq. (2) (Cooper et al. 2004), based on the observation that ports are throughput maximizers (Tongzon 1995). In these models, DMUs on the efficient frontier have an efficiency score of 1. Efficiency scores of sub-optimal DMUs, measured relative to efficient DMUs, have scores >1.

$${\text{max}}\phi - \varepsilon \left( {\sum\limits_{{j = 1}}^{m} {s_{i}^{ - } + \sum\limits_{{r = 1}}^{s} {s_{r}^{ + } } } } \right),{\text{ subject to }}\sum\limits_{{j = 1}}^{n} {\lambda _{j} x_{{ij}} + s_{i}^{ - } = x_{{i0,}} {\mkern 1mu} \quad i = 1,2, \ldots m;} {\text{ }}\sum\limits_{{j = 1}}^{n} {\lambda _{j} y_{{rj}} - s_{r}^{ + } = \phi y_{{r0,}} } {\mkern 1mu} \quad r = 1,2, \ldots s;{\text{ }}\lambda _{j} ,s_{i}^{ - } ,s_{r}^{ + } \ge 0{\mkern 1mu} \quad \forall i,j,r;{\text{ }}\sum\limits_{{j = 1}}^{n} {\lambda _{j} = 1;{\text{ for the DEA-BCC model}}}$$

(2)

where ϕ ₀ is the relative efficiency of DMU₀; $s_{i}^{ - }$ is the input slack variable; $s_{r}^{ + }$ is the output slack variable; and ε is a ‘non-Archimedean’ element, which should be smaller than any positive real number.

Three main input factors for container production considered were as follows: total container berth length (metres), container terminal area (metres²), and total capacity of container cranes (tonnage), as has been used in the previous port studies (e.g. Tongzon and Heng 2005). As an output variable, we have selected the container volume handled (total TEUs) of a port. We acquired port input/output data from Cheon et al. (2010). We also selected the year 2004 for the competition–performance link analysis, and for constructing port competitive pressure data that would match our input/output data.

Control variables

We consider several control variables in estimating the impact of competition on port performance. These include the following:

• Port Size (‘Size’) Researchers have found that economies of scale have prevailed in the port sector over the years and these have significantly influenced port performance (Turner et al. 2004). We control for size effects by including a measure of overall capital assets, proxied by the natural logarithm of linear combinations of container berth numbers, container berth average depths, and crane numbers.

• Network Externalities (‘Network’) A port’s connectedness influences its performance; well-connected ports attract higher container volumes, because shipping networks are more valuable to shipping lines and shippers when ports are connected with other local liner services and spoke ports (McCalla 2003). We control for port connectedness by including the number of direct liner services in ports.

• Global Terminal Operator (‘GTO’) Two dozen GTOs have emerged in the last twenty years; they have been critical sources for the transformation of the structure of the global port sector (Cheon 2009). These specialized entities usually adopt effective investment/management programmes for port infrastructures and superstructures. Since ports involved with GTOs are expected to perform better, we include the percentage of TEUs handled by GTOs in ports’ total container production volume.

• Hinterland Infrastructure (‘Infra’) Ports’ surface infrastructure condition is crucial to port performance (Clark et al. 2004; Turner et al. 2004). If ports’ hinterland transportation networks are unfavourable to cargo movement, shippers/carriers may choose other ports. We consider this effect by using a national-level variable: the percentage of paved roads in the total road network.

• Dummy for China Factor (‘China’) Chinese ports are unusual in terms of their expansion and performance improvement during the last decade, their emerging economic hinterlands, and their new, well-designed container terminals. The dummy variable China can capture the difference in performance between Chinese ports and those of other countries.

Statistical model

As shown in Eq. (3), we specify port performance (DEA) as a quadratic function of competitive pressure (HMA) and the vector of control variables (X) including macro-level institutional competitive pressure for port i, in addition to an error term (u _i ):

$$DEA_{i} = \beta_{1} HMA_{i}^{2} + \beta_{2} HMA_{i} + \beta X_{i} + u_{i},$$

(3)

where β₁ represents a parameter for the quadratic relationship between competitive pressure and port performance.

We specify both HMA and DEA models in this way; that is, as the index values of HMA and DEA increase, the actual intensities of competitive pressure and port performance decrease. Therefore, we expect statistically significant, positive values for β₁ in 2004 to support the inverted-U hypothesis, and values that do not differ from zero for β₁ and β ₂ for 1991 as the contrast group. Table 2 summarizes the descriptive statistics of the variables.

Table 2 Descriptive statistics and correlation coefficients

Results

Impact of competition on performance

Port-specific competitive pressure

Table 3 presents the results of the regression models for 2004 and 1991. The results were checked for sensitivity using a range of distance parameters presented in the next section. The residuals were checked for homoscedasticity and normal distribution assumptions. Table 3 presents the results of the models with a distance parameter of 2, which are fairly consistent with the results from other distance parameters, as shown in Table 4.

Table 3 Regression results (α = 2)

For 2004, Column (a) in Table 3 shows the results of the full model constructed using the HMA-Cities model for competitive pressure and all control variables. The non-linear effect of PSCP on performance (HMA ²) was statistically significant (5%). We examined this effect further by considering whether the non-linearity of competitive pressure could be caused by high-performing Chinese ports, which may distort the full picture of global port competition. We found that the non-linear impact of competitive pressure on performance held, even if the model excluded the Chinese ports entirely (not shown in Table 3). Overall, this indicates that both too much and too little HMA in focal ports can lead to high DEA scores, i.e. overly low/high levels of competitive pressure lead to low port performance: the inverted U-shape.

Although the full model indicated that the impacts of Size, Network, and GTO were not statistically significant, we interpret this as a signal of multicollinearity (the correlation between Size and GTO is 0.452; the correlation between Size and Network is 0.662). We thus specify a combined effect model by multiplying the three variables.¹ The results (Column [b] in Table 3) show that the inverted U-shape between competitive pressure and performance still held, while the combined effect of these three variables on performance was statistically significant; higher GTO investment in ports that increase their container-handling and shipping-network levels leads to lower DEA scores, or higher port performance.

To create the most efficient model of the competitive pressure–performance link, we have reduced the model by using port size instead of the combined effect variable, and without the hinterland infrastructure condition that was not statistically significant in columns (a) and (b) (see Column [c] in Table 3). Overall, the non-linearity of competitive pressure (HMA ²) on performance remained robust in all three models.

Column (d) in Table 3 shows the results of the reduced model using the HMA-Capitals model for competitive pressure. Although non-linearity was not confirmed as strongly as in the results from the HMA-Cities models, it was statistically significant (around the 10% level; p = 0.105).

The signs and statistical significance of the other variables were mostly consistent throughout the four models. The national-level infrastructure condition (PavedRoad) was not statistically significant; the dummy for China was significant at the borderline 10% level, indicating a higher performance of Chinese ports relative to ports in other countries. The national regulatory and institutional environment (ProcWare) was statistically significant and it had a negative sign, which will be discussed in the next section.

Finally, for 1991, due to limited data availability, we specified the reduced models with only one control variable (Size). The results show that there was no statistically significant linear or non-linear relationship between competitive pressure and port performance.

Macro-level institutional competitive pressure

The negative sign for ProcWare indicated that if ports operate in nations that require fewer procedures for building warehouses, they have higher DEA scores or lower port performance. In other words, more restrictive national regulatory environments are related to higher port performance. Since this result is inconsistent with a finding from a previous study on the impact of regulations on port performance (Clark et al. 2004), we scrutinized this relationship further.

First, we tested the non-linearity of ProcWare on performance (not presented here). In particular, we have considered the case where the negative sign may have been a spurious relationship caused by the high-performing Chinese ports operating under high regulatory conditions. When we excluded all Chinese ports from our sample, we found a very weak sign of non-linearity between ProcWare and performance, although we found no evidence of statistical significance in the non-linearity of ProcWare on DEA scores.

We examine this relationship further by using five other variables to capture the national regulatory environments: customs procedures burden, trade barriers prevalence, government regulation burden, and national-level competition intensity in most industries, as measured by seven-point Likert-type scales from the GCRs (Schwab and Porter 2008), and number of days needed to complete procedures for warehouse-building (DaysWare) (World Bank 2005). We found no significant impact of the first four variables from GCR on DEA, but we did find the same negative relationship between DaysWare and DEA. We also examined the non-linearity of the five national-level regulatory condition variables on the dependent variable, and tested the interaction effect between national-level regulatory conditions and PSCP on performance; we found no evidence of non-linearity, however, and no evidence of an interaction effect.

A series of analyses showed that the negative impact of national regulatory and institutional conditions on port performance was not very consistent in several variables. We examined each observation to understand what might have caused the negative impact of ProcWare and DaysWare on the dependent variable. Many countries that require few procedures to build warehouses (<10 administrative steps) are less-developed or have small economies that have experienced low levels of national institutional development. Countries/regions/city/states with high-performing ports, such as Hong Kong, Singapore, Northern Europe, and the United States, have a relatively high number of procedures for building warehouses (about 15–25 steps). Countries with too few administrative steps may also have weak basic institutions for supporting the management of trade, customs, and public sector ports. The weakness of basic institutions at country level may undermine the ability to sustain long-term investment and public sector port operations, which may lead to weak port performance.

Sensitivity analyses

Table 4 presents the parameters of HMA and HMA ² from the reduced models for 2004 and 1991, depending on the different ranges of the distance parameter (α). According to the HMA-Cities model for 2004, non-linearity between competitive pressure and port performance is statistically confirmed for the range of α of 1–3, at the 1–10% statistical significance level. Although the HMA-Capitals models do not show as much statistical strength of non-linearity as the HMA-Cities models do, the HMA-Capitals models also signal non-linearity for the range of α between 2 and 3, at the 10–12% level of statistical significance.

Table 4 Parameters of HMA from the reduced models

When the value of the distance parameter is lower (α = 0.5) than the parameter values between 1 and 3, the competition–performance link becomes positively linear, at around the 10% significance level. Low distance parameter values imply low spatial immobility, partly due to low oil prices in the world crude oil market and overall excellent infrastructural conditions in a region, which makes the scope of port competition broader and more global. Relatively high spatial mobility between ports and hinterlands can make container movement and the container market more flexible and efficient. Thus, linearity in the lower distance parameter values implies that, as container shipping and hinterland markets become more efficient, the non-linear impact of port competition (diseconomies/cost of excessive competitive pressure) may disappear to some extent.

The opposite case occurs when spatial immobility is crucial in shaping HMA, such as when α = 10. The numerator of HMA implies that as the distance between focal ports and hinterland markets increases, ports face exponentially increasing costs and difficulties in reaching markets. The denominator simultaneously implies that focal ports do not face severe competitive forces from competitors for any of their own hinterland markets that are relatively close to those focal ports. The result is that ports can secure local niches through monopolies, in that each port separately occupies certain small segments of the geographic markets. Under this situation, with all else being constant, PSCP may not markedly influence port performance. That situation is quite close to the empirical case of 1991. In that case, ports may not change their operational behaviours, depending on the degree of competitive pressure. When ports operate in local niches, they are guaranteed a certain amount of cargo volume, and their performance is partly shaped ex ante.

The regression models for 1991 indicate that PSCP has no impact on performance throughout most of the range of the distance parameters tested. A weak signal even indicates a negative influence on port performance from a few models. Regardless, most of the results are not statistically significant, at the 10% level.

Overall, the results reasonably support the hypothesis that port-specific competitive pressures had a non-linear impact on port performance in 2004 under certain ranges of distance impedance parameters. In contrast, the models that used the 1991 data revealed little sign of either linear or non-linear impacts.

Discussion and conclusion

Competition–performance linkage

According to previous studies of competitive rivalry, firms that face greater competitive intensity tend to implement various means to improve their positions, including collaboration and ‘action aggressiveness’ (Ferrier 2001). These factors are generally recognized as sources of higher performance. We found a similar positive impact in our study, although we also found that those that face excessively high levels of competitive pressure may lack the capability to secure their outputs given their inputs.

Figure 3 presents a local linear regression (LLR) curve with a kernel smoother, using data from a scatter plot between HMA_(α=2) and DEA for 2004. The DEA scores increase from 2.86 (=e^1.05) to 3.32 (=e^1.2) as HMA increases from the mean level to the one standard deviation (1σ) level. This pattern suggests that to achieve the highest possible level of port performance, ports that face mean-level competitive pressure should expand their output by 2.86 times on average, given their current input levels, whereas ports that face the 1σ lower level of competitive pressure should expand their output by 3.32 times. The net difference of 46% additional output could be the result of an increase in competitive pressure from the 1σ level to the mean level. The effect of the output addition becomes increasingly larger for the next additional unit of higher competitive pressure. For example, a 116% difference in output results from a change of 2σ to 1σ.

Fig. 3

Non-linear impact of competitive pressure on port performance

The presence of ports that cannot exit the market, despite low performance, also triggers greater performance variation among ports that face strong competitive pressure. In Fig. 3, according to the LLR curve, three overall categories of competitive pressure–performance links may be identified: (1) ports that face moderate competitive pressure (−0.7σ to +1.3σ of HMA) and have higher performance than the mean performance level; (2) ports that face too little competitive pressure (above +1.3σ); and (3) ports that face too much competitive pressure (below −0.7σ) and have lower port performance than the mean. The ports that face too little competitive pressure have the lowest performance, with the smallest variance (mean DEA = 1.60, variance = 0.16), thus exhibiting an overall ‘comfortable inefficiency’, while the ports that face too much competitive pressure have the largest variance (mean DEA = 1.27, variance = 0.54).

Port authorities require the capabilities of strategic long-term capital investment to develop long-lived physical assets by collaborating with diverse public and private sector organizations (Cheon et al. 2017; Lindawati et al. 2014). In this sense, the inverted U-shaped impact of competitive pressure on performance may also be associated with Ang’s (2008) finding that firms that face moderate levels of competitive pressure tend to create more frequent and effective collaboration than those that face low or high levels of competitive pressure.

Implications for maritime logistics and port management

Our results can bridge two contrasting views on the role of inter-port competition in port performance. We show that the restructuring of global port markets since the early 1990s has become an impetus for port performance improvement by encouraging inter-port competition. This mechanism is especially effective in contexts where bureaucratic, centralized port policies within monopolistic market structures have dominated many countries’ port industries (Cullinane et al. 2005). On the other hand, we found that too much competitive pressure limits ports to few choices and strategies to manoeuvre under difficult conditions. Intense competition drives ports to bear the risks of excess- or under-capacity (Heaver 1995), because they deal with a series of conflicting forces, including investment in long-lived facilities and sophisticated equipment vis-à-vis shipowners’ short-term interests in minimizing ship turnaround times.

We therefore doubt arguments for the unconditionally positive or negative impact of inter-port competition on port performance. Our results imply that the role of competitive pressure in port operation is influenced by a series of contextual factors: (a) hinterland market conditions, including the position of competitors, and the size and overlap of hinterland market domains under imperfect markets with limited entries/exits and (b) the degree of spatial immobility in the hinterland transportation networks, which may also affect either the linear or non-linear shapes of the effect that competitive pressure has on port performance.

Research limitations and future directions

One limitation of this study is that we only considered a single-product market (containers) and two single-year periods in our assessment of the hypothesis due to the lack of availability of port data at a global scale. We thus cannot detail how the impact of port-specific competitive pressure on performance would be sustained over time or in response to recent changes. Future research should endeavour to address the issue within global port industries. It is also difficult to generate insights into how the implications of our study can be understood in multi-product markets within port and other industries. Future studies could increase the breadth of the competitive pressure to reflect multi-market contacts and could determine the conditions of the relationship between organization-specific competitive pressure and performance.