Abstract
Generalized structured component analysis (GSCA) is a technically well-established approach to component-based structural equation modeling that allows for specifying and examining the relationships between observed variables and components thereof. GSCA provides overall fit indexes for model evaluation, including the goodness-of-fit index (GFI) and the standardized root mean square residual (SRMR). While these indexes have a solid standing in factor-based structural equation modeling, nothing is known about their performance in GSCA. Addressing this limitation, we present a simulation study’s results, which confirm that both GFI and SRMR indexes distinguish effectively between correct and misspecified models. Based on our findings, we propose rules-of-thumb cutoff criteria for each index in different sample sizes, which researchers could use to assess model fit in practice.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Component-based structural equation modeling (SEM) is a general multivariate framework for evaluating the relationships between observed variables and their weighted composites (i.e., components). This SEM domain differs from factor-based SEM used to investigate the relationships between observed variables and common factors rather than components (e.g., Jöreskog and Wold 1982; Rigdon 2012; Tenenhaus 2008).Footnote 1 Covariance structure analysis (CSA; Jöreskog 1970) is a standard statistical approach to factor-based SEM, whereas partial least squares path modeling (PLSPM; Lohmöller 1989; Wold 1982) and generalized structured component analysis (GSCA; Hwang and Takane 2004) are full-fledged approaches to component-based SEM.
Although SEM has often been equated with factor-based SEM (Hair et al. 2011), our viewpoint coincides with that the two SEM domains are conceptually distinct, and their statistical methods should be used for estimating models with representations of constructs, which are consistent with what the methods assume (e.g., Hair and Sarstedt 2019; Hwang et al. 2020; Rigdon et al. 2017; Sarstedt et al. 2016). That is, CSA should be chosen for estimating models in which factors represent the unobservable concepts of interest, whereas PLSPM and GSCA should be used for estimating models where composites serve as such representations.
While PLSPM and GSCA share the same aim, which is estimating relationships between observed variables and components representing theoretical concepts of interest, they differ in several respects (Hwang et al. 2020).Footnote 2 A fundamental difference relates to the model specification and estimation. In PLSPM, model specification involves measurement and structural models. When estimating these models, PLSPM does not combine them into a single algebraic formulation (e.g., Tenenhaus et al. 2005), but divides the parameters into two sets, and estimates each set sequentially through two estimation stages (e.g., Lohmöller 1989). This characteristic, however, complicates the assessment of model fit, as no unique criterion is optimized according to which the degree of optimization can be assessed. While several model fit indexes have been proposed in the PLSPM context, researchers have long complained that these indexes are based on parameters that are not explicitly optimized as part of the algorithm (e.g., Hair et al. 2019; Lohmöller 1989; Sarstedt et al. 2017). Consequently, any statement about a model’s quality and decisions regarding potential model modifications based on existing model fit indexes are questionable when using PLSPM (Hair et al. 2019).
Conversely, model specification in GSCA involves three sub-models (i.e., measurement, structural, and weighted relation models), which are being combined into a single equation called the GSCA model. A single objective function is directly derived from the GSCA model, which is consistently minimized to estimate all the model parameters (Hwang and Takane 2004). GSCA is therefore regarded as a full information method utilizing all the information available in the entire system of equations (Tenenhaus 2008). The availability of a single objective function has the advantage that the overall model quality can be readily assessed, because the function value arises from the GSCA-based model estimation.
Research has suggested overall model fit measures for GSCA, such as the goodness-of-fit index (GFI; Jöreskog and Sörbom 1986) and the standardized root mean square residual (SRMR), which quantify the discrepancies between the sample covariances and the implied ones derived from the parameters. The indexes are scaled such that the GFI values close to one and the SRMR values close to zero indicate an acceptable fit level. Both indexes are well-known from the factor-based SEM context, where specific cutoff values have long been established. Specifically, researchers usually assume a cutoff value of .08 for the SRMR (e.g., Hu and Bentler 1999) and .90 for the GFI (e.g., McDonald and Ho 2002). However, it is unclear whether GSCA could adopt the same GFI and SRMR cutoff values (Hwang and Takane 2014, p. 29).
To our knowledge, no study has investigated the performance of the two fit indexes in GSCA. Consequently, there are no cutoff criteria that researchers could employ to evaluate their GSCA models’ fit. Addressing this concern, we conduct a simulation study to examine the indexes’ efficacy regarding differentiating between correct and misspecified models. Based on our results, we identify concrete cutoff values for each of the indexes, which minimize Type I and II error rates under different conditions.
The paper continues with this structure: After a brief description of GSCA, which addresses model specification and parameter estimation, we explain how to derive the GSCA model’s implied covariance matrix. Building on this explanation, we explain the GFI and SRMR indexes. We subsequently describe our simulation study’s design and report the results. Finally, we discuss the indexes’ behaviors, derive cutoff values, and highlight potential issues that researchers need to consider when employing the indexes.
Generalized structured component analysis
Model specification and estimation
In model specification, GSCA involves three sub-models: measurement, structural, and weighted relation models (Hwang and Takane 2014, Sect. 2.1). Let z and γ denote J by 1 and P by 1 vectors of J observed variables and P components, respectively, both of which are assumed to be standardized (i.e., they have zero means and unit variances). The measurement model is employed to express the relationships between observed variables and components, which can be generally written as
where C is a J by P matrix consisting of loadings relating observed variables to their components, and ε is a J by 1 residual vector of z. The structural model is used to specify the relationships between the components and can generally be expressed as
where B is a P by P matrix of path coefficients relating the components, and ζ is a P by 1 residual vector of γ. In addition, GSCA explicitly defines γ as components (i.e., weighted composites of observed variables) as follows:
where W is a P by J matrix of weights assigned to observed variables. This weighted relation model constitutes another submodel.
In the measurement model (1), GSCA does not specify an observed variable’s random measurement error explicitly in that the ε term simply includes observed variables’ residuals unexplained by components, as in linear regression. This is different from factor-based SEM, which divides each observed variable’s variance into two parts: The common variance shared with other observed variables in the measurement model of a construct, and the unique variance that consists of both specific variance and random measurement error variance (Mulaik 2010, pp. 132–133). Nonetheless, when creating a component in the weighted relation model (3), the unique variance of an observed variable, which includes the variance of its random measurement error, is much less counted than the shared variance (Mulaik 2010, p. 83). Consequently, forming a component plays a role in reducing random measurement error (Rigdon 2012). If researchers are interested in explicitly taking into account random measurement error in (3), they can apply Bayesian GSCA (Choi and Hwang 2020), where a component is obtained after each observed variable’s random measurement error is removed. It is also worth noting that factor-based SEM specifies a unique variance only, which is the sum of specific and random measurement error variances, being unable to distinguish between the two variances.
GSCA can have several linear models comprising observed variables and components as special cases (Hwang and Takane 2014, Sect. 2.5). For example, the combination of Eqs. (1) and (3) is equivalent to the confirmatory (principal) component model in the sense that weighted composites or components of observed variables in (3) are obtained in such a way that the components explain the maximum variances of the observed variables, reflected by loadings in (1). Note that some of weights and loadings are typically constrained to be zero based on prior theories or hypotheses (e.g., ten Berge 1993; Hair et al. 2020; Kiers et al. 1996). This is comparable to the confirmatory factor analysis model in factor-based SEM, where common factors replace components.
GSCA combines the three sub-models into a single equation as follows:
where I is an identity matrix, V = \(\left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ {\mathbf{W}} \\ \end{array} } \right]\), A = \(\left[ {\begin{array}{*{20}c} {\mathbf{C}} \\ {\mathbf{B}} \\ \end{array} } \right]\), and e = \(\left[ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}} \\ {{\varvec{\upzeta}}} \\ \end{array} } \right]\), which is called the GSCA model (Hwang and Takane 2014, p. 19). Per default, GSCA does not make distributional assumptions on e or impose any further constraints on (4). However, in component-based SEM, observed variables per component are typically assumed to be correlated to each other, rendering the covariance matrix of ε to be block-diagonal (e.g., Bollen and Bauldry 2011; Cho and Choi 2020; Dijkstra 2017; Grace and Bollen 2008), although GSCA does not need to assume a specific covariance structure of observed variables in advance, leaving them to be (un)correlated freely. PLSPM also includes measurement and structural models, but does not involve the weighted relation model explicitly, although it estimates γ as weighted composites of observed variables during the parameter estimation procedure (e.g., McDonald 1996). That is, PLSPM does not integrate its sub-models into a single algebraic formulation (e.g., Tenenhaus et al. 2005).
As shown in Eq. (4), the GSCA model includes loadings (C), path coefficients (B), and weights (W) as parameters. Let ei denote the residual term in Eq. (4) for a single observation of a sample of N observations (i = 1, …, N). To estimate all the parameters, GSCA aims to minimize the following least squares objective function
subject to the standardization constraints on components (i.e., diag\((\varvec{\upgamma\upgamma}^{\prime})\) = NI). This objective function is directly derived from the GSCA model. An iterative least squares algorithm, called alternating least squares (de Leeuw et al. 1976), is utilized to minimize the objective function without taking recourse to distributional assumptions, such as observed variables’ multivariate normality. This algorithm repeats two steps, each of which estimates a set of parameters in a least squares sense with the other sets fixed, until the difference in the values of (5) between two consecutive iterations becomes negligible (e.g., smaller than 10–5). Specifically, in one step, weights are updated while loadings and path coefficients are considered fixed temporarily. In the other step, loadings and path coefficients are updated while weights are considered fixed temporarily (see Hwang and Takane 2014, Sect. 2.2).
Model fit indexes
GSCA offers two overall fit indexes that reflect the discrepancies between the sample covariances and the model-implied covariances. These discrepancies are based on the parameter estimates on convergence (also called the reproduced covariances): GFI and SRMR (Hwang and Takane 2014, p. 28). We assume that cov(ε, ζ) = 0. The two indexes are directly derived from Eq. (4). Specifically, we can re-express (4) as follows:
where T = \(\left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{C}} \\ {\mathbf{0}} & {\mathbf{B}} \\ \end{array} } \right]\). The implied covariance matrix of z, denoted by Σ, is then given as
where G = [I, 0], and \({{E}}({\mathbf{ee}}^{\prime})\) is a block-diagonal covariance matrix of e.
Let S and \({\hat{\mathbf{\Sigma }}}\) denote the sample and the reproduced covariance matrices. Let sij and \(\hat{\sigma }_{ij}\) respectively denote an observed covariance in S and the corresponding reproduced covariance in \({\hat{\mathbf{\Sigma }}}\). Thereafter, the GFI and SRMR are obtained as
As shown in the above formulas, GFI values close to one and SRMR values close to zero denote a small degree of the covariance discrepancies, which allows them to be indicative of an acceptable fit (e.g., Hu and Bentler 1999; Hwang and Takane 2014; McDonald and Ho 2002). However, how the two indexes behave, and which values could be indicative of an acceptable fit in GSCA are not yet known. In the next section, we conduct a simulation study to address these issues.
Simulation study
Design
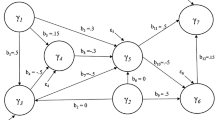
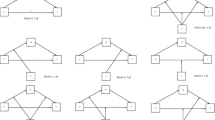
We considered a five-component model, with each component associated with five observed variables, in order to represent a relatively complex measurement model setting. Following Hu and Bentler's (1999) study, we did not assume path analytic relationships between the five components, indicating that our specified model was a confirmatory component model. We also considered a misspecification of the model, with each component incorrectly linked to one or two observed variables. A component is a linear deterministic function of observed variables, which means that adding different observed variables to a component changes its meaning substantively (e.g., Jarvis et al. 2003). Figure 1 shows the correct and misspecified models. Weights were also assigned to all the observed variables in order to yield components; see Eq. (3). In the correct model, we fixed the weights of the observed variables per component to .24, .24, .28, .32, and .32, and the corresponding loadings to .6, .6, .7, .8, and .8. These weights and loadings were chosen to consider that each observed variable should contribute comparably to forming its component, reflected by a similarly sizeable weight, and the component should in turn explain the variance of its observed variable well, signified by a relatively large loading.
Furthermore, we considered three levels of component correlations (r = 0, .2, and .4) and five different sample sizes (N = 100, 200, 500, 1000, and 2000). To ensure the model’s discriminant validity (Franke and Sarstedt 2019), we kept the component correlation levels lower than each loading value. Note that not all the components were assumed to be correlated with one another in order to ensure that their covariance matrix is positive definite. For each combination of the experimental conditions, we generated 1000 random samples from a multivariate normal distribution with zero means and the model-implied covariance matrix derived from Cho and Choi (2020). We explain the procedure of deriving the model-implied covariance matrix in the Appendix.
Results
Our analysis aims to assess whether the GFI and SRMR differentiate between correct and misspecified models and to identify cutoff values that minimize Types I and II error rates under different conditions. As in Hu and Bentler (1999), we assessed a Type I error rate for a given cutoff value of the GFI by counting how frequently in the 1000 samples each fitted correct model’s GFI value was smaller than the cutoff value, thus resulting in the correct model being rejected. Similarly, we computed a Type II error rate for the same cutoff value by counting how frequently each fitted misspecified model’s GFI value was greater than the cutoff, thus failing to reject the misspecified model. For the SRMR, we calculated the Types I and II error rates of a given cutoff value by counting how frequently over the samples each fitted correct model’s SRMR value was greater than the cutoff value and how frequently the fitted misspecified model’s SRMR was smaller than the cutoff.
Table 1 presents the averages and standard deviations of the GFI and SRMR values of the correct and misspecified models fitted to 1000 samples generated under each combination of the experimental conditions. As expected, the correct model’s GFI value was large (e.g., > .90), approaching one when the sample size became large (Table 1). This GFI pattern in the correct model remains the same across the different levels of component correlations (r). At the same time, the misspecified model’s GFI value was, on average, smaller than .90 when the component correlation was equal to or smaller than .2, although it tended to increase with the sample size. The same pattern was observed for r = .4, although the GFI value of the misspecified model was slightly greater than .90 in large samples (N ≥ 1000). Furthermore, as expected, the correct model’s SRMR value was small overall (e.g., < .08) and approached zero as the sample size increased, regardless of the component correlation’s degree. In general, the misspecified model’s SRMR value was greater than .08 in all conditions, although it tended to be slightly smaller when the sample size increased.
Table 2 shows the Types I and II error rates for different cutoff values of the GFI in the different conditions. As expected, a larger GFI cutoff value tended to produce a larger Type I error rate (i.e., more rejections of the correct model) in small sample sizes (N ≤ 200), regardless of the component correlation’s level. At the same time, when the sample size increased, all the cutoff values resulted in a zero Type I error rate. This result is consistent with our previous finding that the correct model’s average GFI values were rather large in moderate and large sample sizes (Table 1). Moreover, a larger GFI cutoff value tended to produce a smaller Type II error rate (i.e., more rejections of the misspecified model). When r = 0, Type II error rates for all the cutoff values were zero across the sample sizes, which was expected, because the misspecified model’s average GFI values were smaller than all the cutoff values in this condition (Table 1). Table 2 also presents the average of Types I and II error rates for each GFI cutoff value, which shows which cutoff value resulted in the minimum average of both error rates.
Table 3 shows the Types I and II error rates for different SRMR cutoff values in the same conditions. As expected, a smaller SRMR cutoff value resulted in a larger Type I error rate in small sample sizes (N ≤ 200), regardless of the component correlation’s level. When the sample size was moderate or large (N ≥ 500), all of the cutoff values led to zero Type I error rates. This is consistent with our previous finding that the correct model’s average SRMR values were quite small in these sample sizes (Table 1). As expected, a smaller SRMR cutoff value resulted in a smaller Type II error rate. Table 3 also shows the average of Types I and II error rates for each SRMR cutoff value.
Figure 2 presents the averages of Types I and II error rates for different GFI and SRMR cutoff values across the sample sizes, which we calculated by averaging each cutoff value’s mean Types I and II error rates over the component correlation’s three levels. In respect of N = 100, a GFI cutoff value of .89 resulted in the minimum average of Types I and II error rates, whereas in respect of N > 100, using a GFI cutoff value of .93 produced the minimum average of Types I and II error rates. On the other hand, in respect of N = 100, using an SRMR cutoff value of .09 led to the minimum average of Types I and II error rates, whereas in respect of N > 100, using an SRMR cutoff value of .08 resulted in the minimum average of Types I and II error rates. In addition, in respect of N = 100, the minimum average of Types I and II error rates—obtained by using SRMR = .09 (.001)—was smaller than that obtained by using GFI = .89 (.014). However, in respect of N > 100, both the SRMR = .08 and the GFI = .93 provided the same minimum average (i.e., zero).
Average error rates of GFI and SRMR cutoff values in different sample sizes. Note: The figure shows the averages of Types I and II error rates for different GFI and SRMR cutoff values aggregated over three levels of component correlation in each sample size. Plus: 100, asterisk: 200, open circle 500, open square 1000, and open diamond 2000
We also examined how the average Types I and II error rates changed in different combinations of the GFI and SRMR cutoff values. As shown in Table 4, in respect of N = 100, using an SRMR cutoff value of .09 in combination with GFI cutoff values from .85 to .89 resulted in a smaller minimum average of Types I and II error rates than that obtained by employing a GFI (.014) cutoff value of .89, whereas it was virtually identical to that obtained by using an SRMR cutoff value of .09. Conversely, in respect of N > 100, using a combination of SRMR = .08 and GFI = .93 yielded the same average error rate (i.e., zero) as using them separately. In addition, in this case, using an SRMR cutoff value of .08 seemed to minimize the average value of Types I and II error rates, no matter which GFI cutoff value we chose. This also applies to the GFI. That is, using a GFI cutoff value of .93 resulted in the minimum average of Types I and II error rates, regardless of the SRMR cutoff values.
Conclusions
Our simulation study suggests that GFI and SRMR are effective in discriminating between correct and misspecified component models when estimating the models using GSCA. With an increase in sample size, the GFI and SRMR respectively and consistently converge to one and zero in the correct model, whereas they tended to differ from their optimal values in a misspecified model. In addition, our results suggest that the sample size is relevant for GFI’s and SRMR’s cutoff selection. Although it is difficult to provide a specific cutoff value per index for every possible sample size and research setting (Niemand and Mai 2018), our results suggest the following:
-
When N = 100, researchers may choose a GFI cutoff value of .89 and an SRMR cutoff value of .09. That is, a GFI ≥ .89 and an SRMR ≤ .09 indicate an acceptable level of model fit. Although both indexes can be used to assess model fit, using the SRMR with the above cutoff value (i.e., SRMR ≤ .09) may be better than using the GFI with the suggested cutoff value (i.e., GFI ≥ .89), because the former generally resulted in Type I and Type II error rates having a smaller average. In addition, if SRMR ≤ .09, then a GFI cutoff value of ≥ .85 may still be indicative of an acceptable fit.
-
When N > 100, researchers may choose a GFI cutoff value of .93 and an SRMR cutoff value of .08. In this case, there is no preference for one index over the other, or for using a combination of the indexes over using them separately. Each index’s suggested cutoff value may be used independently to assess the model fit. That is, a GFI ≥ .93 or an SRMR ≤ .08 indicates an acceptable fit.
By investigating the performance of the GFI and SRMR indexes systematically through the analyses of simulated data under different experimental conditions, our study contributes to establishing an empirical basis for using the indexes to evaluate component models in GSCA. Nevertheless, similar to all simulation studies, this study is limited in scope, as it only considers a few experimental conditions and a relatively simple model, which, however, has been well-established in prior research’s simulations to evaluate model fit indexes (e.g., Hu and Bentler 1999; Marsh et al. 2004; Sivo et al. 2006). Researchers should not use the characterized cutoff criteria for GFI and SRMR as golden rules for making decisions on model fit assessment in GSCA. Just like in applications of factor-based SEM, researchers should use these cutoff criteria cautiously as reference points across different sample sizes and model set-ups (Niemand and Mai 2018). It is also worth noting that examining overall fit indexes, such as the GFI and the SRMR, is merely one aspect of model evaluation, which also needs to consider local fit measures such as FITM and FITS (Hwang et al. 2020). An acceptable model fit does not necessarily guarantee the model’s plausibility and this judgement should be made based on substantive theory (Byrne 2001, p. 88). Furthermore, a well-fitting model does not necessarily warrant enough predictive power, which is important to substantiate practical recommendations derived from any model (Hair et al. 2019; Liengaard et al. 2020).
Notes
References
Bollen, K.A., and S. Bauldry. 2011. Three Cs in measurement models: Causal indicators, composite indicators, and covariates. Psychological Methods 16 (3): 265–284.
Byrne, B.M. 2001. Structural equation modeling with AMOS: Basic concepts, applications, and programming. Mahwah, NJ: Erlbaum.
Cho, G., and J.Y. Choi. 2020. An empirical comparison of generalized structured component analysis and partial least squares path modeling under variance-based structural equation models. Behaviormetrika 47 (1): 243–272.
Choi, J.Y., and H. Hwang. 2020. Bayesian generalized structured component analysis. British Journal of Mathematical and Statistical Psychology 73 (2): 347–373.
de Leeuw, J., F.W. Young, and Y. Takane. 1976. Additive structure in qualitative data: An alternating least squares method with optimal scaling features. Psychometrika 41 (4): 471–503.
Dijkstra, T.K. 2017. A perfect match between a model and a mode. In Partial least squares path modeling: Basic concepts, methodological issues and applications, ed. H. Latan and R. Noonan, 55–80. Berlin: Springer.
Franke, G., and M. Sarstedt. 2019. Heuristics versus statistics in discriminant validity testing: A comparison of four procedures. Internet Research 29 (3): 430–447.
Grace, J.B., and K.A. Bollen. 2008. Representing general theoretical concepts in structural equation models: The role of composite variables. Environmental and Ecological Statistics 15 (2): 191–213.
Hair, J.F., M.C. Howard, and C. Nitzl. 2020. Assessing measurement model quality in PLS-SEM using confirmatory composite analysis. Journal of Business Research 109: 101–110.
Hair, J.F., C.M. Ringle, and M. Sarstedt. 2011. PLS-SEM: Indeed a silver bullet. Journal of Marketing Theory and Practice 19 (2): 139–152.
Hair, J.F., J.J. Risher, M. Sarstedt, and C.M. Ringle. 2019. When to use and how to report the results of PLS-SEM. European Business Review 31 (1): 2–24.
Hair, J.F., and M. Sarstedt. 2019. Factors versus composites: Guidelines for choosing the right structural equation modeling method. Project Management Journal 50 (6): 619–624.
Hu, L., and P.M. Bentler. 1999. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal 6 (1): 1–55.
Hwang, H., N.K. Malhotra, Y. Kim, M.A. Tomiuk, and S. Hong. 2010. A comparative study on parameter recovery of three approaches to structural equation modeling. Journal of Marketing Research 47 (4): 699–712.
Hwang, H., M. Sarstedt, J.H. Cheah, and C.M. Ringle. 2020. A concept analysis of methodological research on composite-based structural equation modeling: Bridging PLSPM and GSCA. Behaviormetrika 47 (1): 219–241.
Hwang, H., and Y. Takane. 2004. Generalized structured component analysis. Psychometrika 69 (1): 81–99.
Hwang, H., and Y. Takane. 2014. Generalized structured component analysis: A component-based approach to structural equation modeling. New York, NY: Chapman and Hall/CRC Press.
Jarvis, C.B., S.B. MacKenzie, and P.M. Podsakoff. 2003. A critical review of construct indicators and measurement model misspecification in marketing and consumer research. Journal of Consumer Research 30 (2): 199–218.
Jöreskog, K.G. 1970. A general method for analysis of covariance structures. Biometrika 57 (2): 239–251.
Jöreskog, K.G., and D. Sörbom. 1986. PRELIS: A program for multivariate data screening and data summarization.
Jöreskog, K.G., and H. Wold. 1982. The ML and PLS techniques for modeling with latent variables: Historical and comparative aspects. In Systems under indirect observation: Causality, structure, prediction, part I, ed. H. Wold and K.G. Jöreskog, 263–270. Amsterdam, Netherlands: North Holland.
Kiers, H.A.L., Y. Takane, and J.M.F. ten Berge. 1996. The analysis of multitrait-multimethod matrices via constrained components analysis. Psychometrika 61 (4): 601–628.
Liengaard, B., Sharma, P.N., Hult, G.T.M., Jensen, M.B., Sarstedt, M., Hair, J.F., and Ringle, C.M. (2020) Prediction: Coveted, yet forsaken? Introducing a cross-validated predictive ability test in partial least squares path modeling. forthcoming.
Lohmöller, J.B. 1989. Latent variable path modeling with partial least squares. New York, NY: Springer-Verlag.
Marsh, H.W., K.-T. Hau, and Z. Wen. 2004. In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural Equation Modeling: A Multidisciplinary Journal 11 (3): 320–341.
McDonald, R.P. 1996. Path analysis with composite variables. Multivariate Behavioral Research 31 (2): 239–270.
McDonald, R.P., and M.-H.R. Ho. 2002. Principles and practice in reporting structural equation analyses. Psychological Methods 7 (1): 64–82.
Mulaik, S. 2010. Foundations of factor analysis, 2nd ed. New York, NY: Chapman and Hall/CRC Press.
Niemand, T., and R. Mai. 2018. Flexible cutoff values for fit indices in the evaluation of structural equation models. Journal of the Academy of Marketing Science 46 (6): 1148–1172.
Petter, S. 2018. “Haters Gonna Hate”: PLS and Information Systems Research. ACM SIGMIS Database: the DATABASE for Advances in Information Systems 49 (2): 10–13.
Rhemtulla, M., R. van Bork, and D. Borsboom. 2020. Worse than measurement error: Consequences of inappropriate latent variable measurement models. Psychological Methods 25 (1): 30–45.
Rigdon, E.E. 2012. Rethinking partial least squares path modeling: In praise of simple methods. Long Range Planning 45 (5–6): 341–358.
Rigdon, E.E., M. Sarstedt, and C.M. Ringle. 2017. On comparing results from CB-SEM and PLS-SEM: Five perspectives and five recommendations. Marketing ZFP 39 (3): 4–16.
Sarstedt, M., J.F. Hair, C.M. Ringle, K.O. Thiele, and S.P. Gudergan. 2016. Estimation issues with PLS and CBSEM: Where the bias lies! Journal of Business Research 69 (10): 3998–4010.
Sarstedt, M., C.M. Ringle, and J.F. Hair. 2017. Partial least squares structural equation modeling. In Handbook of market research, ed. C. Homburg, M. Klarmann, and A. Vomberg, 1–40. Cham: Springer.
Sivo, S.A., X. Fan, E.L. Witta, and J.T. Willse. 2006. The search for ‘Optimal’ cutoff properties: Fit index criteria in structural equation modeling. The Journal of Experimental Education 74 (3): 267–288.
ten Berge, J.M.F. 1993. Least squares optimization in multivariate analysis. Leiden, Netherlands: DSWO Press.
Tenenhaus, M. 2008. Component-based structural equation modelling. Total Quality Management and Business Excellence 19 (7–8): 871–886.
Tenenhaus, M., V. Esposito Vinzi, Y.-M. Chatelin, and C. Lauro. 2005. PLS path modeling. Computational Statistics & Data Analysis 48 (1): 159–205.
Wold, H. 1982. Soft modeling: The basic design and some extensions. In Systems under indirect observation: Causality, structure, prediction, part II, ed. K.G. Jöreskog and H. Wold, 1–54. Amsterdam, Netherlands: North Holland.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The procedure of deriving the model-implied covariance matrix of observed variables in the simulation study
Appendix: The procedure of deriving the model-implied covariance matrix of observed variables in the simulation study
Let zp denote a Jp by 1 vector of observed variables forming the pth component and Σp denote a Jp by Jp covariance matrix of zp (p = 1, 2, ..., P). Let cp denote a Jp by 1 vector of loadings of the pth component. Let wp denote a 1 by Jp vector of weights for the pth component. Let εp denote a Jp by 1 vector of residuals for zp and Ψp denote a Jp by Jp covariance matrix of εp. Let Σ, Φ, and Ψ denote J by J, P by P, and J by J covariance matrices of z, γ, and ε, respectively.
Given the prescribed values of Σp and Φ, wp and cp are determined in such a way that components can maximize the explained variances of their observed variables, as follows.
where u1 is the first eigenvector of Σp. Then, Ψp is determined by
Lastly, Σ is obtained by
where C = diag(c1, c2, ... , cP), and Ψ = diag(Ψ1, Ψ2, ... , ΨP).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cho, G., Hwang, H., Sarstedt, M. et al. Cutoff criteria for overall model fit indexes in generalized structured component analysis. J Market Anal 8, 189–202 (2020). https://doi.org/10.1057/s41270-020-00089-1
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/s41270-020-00089-1