Introduction

The 2008–2009 and more recent financial crises have spurred renewed interest in risk management and approaches to capital allocation. The Markowitz (1952) approach, for long the mainstay of MBA textbooks, has been criticised for the maintained hypotheses that returns are well-described by a Gaussian distribution or that investors have mean-variance (MV) utility.Footnote 1,Footnote 2 With this in mind, we provide closed-form solutions for the gain in expected utility from accounting for non-normality in a mean-variance framework. Our analytical approach circumvents the pitfalls that can thwart empirical studies. We make assumptions about return and volatility generating models that change from very strong assumptions to versions closer to empirical data. Readers should be aware that we do not claim that each model is an accurate representation of the returns faced by asset managers; rather, such an approach allows us, at least partially to decompose the changes in expected utility that arise. We quantify the gain in expected utility for both international and domestic investors. First, we show that there are economically significant gains in mean-variance utility from accounting for non-normality commensurate with typical mutual fund fees. Second, we find that most of the gains in expected utility derive from accounting for stochastic volatility. Fleming et al. (2001, 2003, 2012), Gomes (2007), Han (2006), Busse (1999), and Kim and In (2012) all provide empirical evidence that accounting for stochastic volatility adds economic value. Our analytical model identifies the potential origin of this uplift in performance. Our result provides justification for an increased use of conditional volatility models, showing real economic gains for investors.

The remainder of this paper is organised as follows. In the section “Non-Normality and Investment”, we survey literature relating to investor preferences and the non-Gaussian characteristics of financial data. In the section “Analytical Framework”, we set out our stochastic return models and analytical approach. In the section “Derivation of Propositions”, we propose two distributions for our state variables that control asymmetry and stochastic volatility. Next, we derive closed-form solutions for the gain in expected utility from accounting for non-normality and then provide two empirical applications for a domestic and an international investor, before concluding.

Non-normality and investment

It has long been established that the returns of financial assets depart from normality. Mandelbrot (1963) documented extreme departures from normality for commodity prices, “warranting a radically new approach to the problem of price variation”. Analysing large cap equities, Fama (1963) reported that 5-standard deviation events occur 2000 times more often than the Gaussian distribution predicts.Footnote 3 Further, financial data tend to contain more extreme negative returns than extreme positive returns: the return distribution is asymmetric or skewed. In common parlance, “busts” are more common than “booms” (Beedles 1979; Alles and Kling 1994). Mandelbrot (1963) also identified volatility clustering for commodities where “large changes tend to be followed by large changes, of either sign, and small changes tend to be followed by small changes”. More recent research reveals asymmetric dependence structures between assets. In the international context, Karolyi and Stulz (1996) find that the dependence between US and Japanese stocks increases during large shocks to the respective markets. Within the US market, Ang and Chen (2002) show that the dependence between individual stocks and the aggregate market index is significantly higher for extreme downside moves than for extreme upside moves of the index.Footnote 4

Throughout our analysis, we consider a single investor with mean-variance utility. While the mean-variance assumption is largely normative in practice, our use of the mean-variance utility assumption is motivated in three ways. First, despite it being well established that returns are non-Gaussian and that investors are concerned with higher moments, the mean-variance approach remains ubiquitous. In a survey of investment managers, Amenc et al. (2011) find that most investors do not employ extreme risk measures, instead relying on the Gaussian distribution or not quantifying tail events whatsoever (see also Fabozzi et al. 2007). Second, the use of the mean-variance approximation is also justified through a second-order Taylor series expansion of expected utility. Samuleson’s (1970) Fundamental Approximation Theorem shows that for “compact” probabilities involving less and less risk, the mean-variance approach becomes increasingly accurate. Third, the mean-variance assumption is consistent with exponential utility when returns are normally distributed. Finally, in addressing the claims of DeMiguel et al (2009) that 1/N portfolios outperform optimised ones, Allen et al. (2019) show that M-V approaches can outperform more passive 1/N approaches with minimal forecasting ability. Although we formally compare the expected utility of “distinct” informed and uninformed investors, this is consistent with treating them as the same entity with and without information. This is important as comparing utility across different individuals leads to a number of additional requirements, which we do not wish to assume.

Analytical framework

Stochastic return models

The relationship between conditional returns and conditional variance intuitively plays an important role in determining the effect of accounting for stochastic volatility. If, for example, conditional returns and conditional variance are unrelated, it should be possible to increase utility by increasing exposure when risk is low, thereby capturing higher returns, and decreasing exposure when risk is high. Under the efficient market hypothesis, agents must be compensated for systematic risk and hence it follows that the conditional variance of market returns should be positively related to conditional excess returns. Empirical evidence, however, is inconclusive. Pindyck (1984), French et al. (1987), and Ghysels et al. (2005) find a positive relationship, while Campbell (1987), Glosten et al. (1993), Whitelaw (1994), (2003) and Brandt and Kang (2004) document negative relationships. Given this lack of a clear relationship between risk and return, we use two stochastic return models with different assumptions on the relationship between conditional variance and conditional excess returns. Both stochastic representations accommodate skew, heavy tails, tail dependence and stochastic volatility. Although the term unconditional expected mean variance may sound as if it has a redundancy, we use it to remind the reader that we have accounted for all variation in state variables. We also assume, in effect, three information sets for each of our different models. Knowing the full set and taking expectations is denoted by a subscript O (“Omniscient”), repeating the exercise with “possible” information is denoted by the subscript I (Informed), and for knowing less than the informed set, we use the subscript U (Uninformed). The precise details of each information set depend upon the model structure that we assume. This will change throughout the paper. Readers may wish to peruse Table 1 which sets out a sense of how this works.

Table 1 Unconditional and conditional moments under Model 1 with skew and stochastic volatility
Full size table

In the first model, we assume that conditional mean returns and conditional variance are independent. The first stochastic representations is given by

$$\begin{array}{*{20}{c}} {Model\;1:\quad {r_t} = {s_{1,t}}\mu + s_{2,t}^\frac{1}{2}H{z_t}} \end{array}$$
(1)

where \({r_t}\) is a vector of returns, \(\mu\), is the vector of unconditional mean returns, H is the Cholesky decomposition of the covariance matrix, \({\Sigma }\), \({s_1}\) and \({s_2}\) are state variables, and Ω is the unconditional covariance matrix.

The vector \({z}_{t}\) consists of iid normal variables. Hereinafter, we drop the time subscript for the state variables. For clarity, we initially drop information subscripts for expectations, showing them in later models. In both models, the expected values of the two state variables are: \(E\left[{s}_{1}\right]=E\left[{s}_{2}\right]=1\) and the two state variables are independent of each other, \(E\left[{s}_{1}{s}_{2}\right]=1\), and independent of \({z}_{t}\). In Model 1, when \({s}_{1}>1\), the conditional expected return is greater than \(\mu\). Similarly, when \({s}_{2}>1\), the conditional covariance matrix is increased in the sense that the difference between the new and old matrices is positive semi-definite. The first model subsumes many notable cases. If \({s}_{1}=1\) and \({s}_{2}=1\), we recover the Gaussian distribution; if \({s}_{1}={s}_{2}\sim {N}^{-}\left(\lambda ,\chi ,\psi \right)\) where \({N}^{-}\) denotes the generalised inverse Gaussian distribution,Footnote 5 we have the central generalised hyperbolic distribution;Footnote 6 if \({s}_{1}={s}_{2}\sim IG\left(v/2,v/s\right)\), where \(IG\) denotes the inverse gamma distribution, and \(v\) is the degrees of freedom parameter, we have the central multivariate skewed-t distribution of DeMarta and McNeil (2005).

The first state variable, \({s}_{1}\), introduces skew, heavy tails and tail dependence to the unconditional distribution with jumps occurring simultaneously across all assets. The second state variable, \({s}_{2}\), introduces time-varying volatility and heavy tails to the unconditional distribution. In this way, we capture the four stylised facts of financial assets: heavy tails, negative skew, volatility-clustering and tail dependence.

In the second model, we assume that conditional returns and the conditional variance of the market are positively dependent, in line with standard equilibrium theory. The second stochastic model is given by

$$\begin{array}{*{20}{c}} {Model\;2:\quad {r_t} = s_2^\frac{1}{2}\left( {{s_1}\mu + H{z_t}} \right)} \end{array}$$
(2)

Under the second model, assets react differently to information depending on the state of the market. When volatility is high, a given negative shock, \({s}_{1}<1\), will result in a larger price decline than when volatility is low.

Informed and uninformed investors

To quantify the benefits from accounting for non-normality, we assume the existence of informed and uninformed investors (or, equivalently, consider an investor with and without information, given our prior caveat). The informed investor is aware that the return distribution is skewed and that volatility is stochastic, whereas the uninformed investor assumes that returns are i.i.d. multivariate Gaussian. We therefore assume that informed investors are aware of the state variable, \({s}_{1}\), but are unaware of the value of \({s}_{1}\) at any point in time. This is consistent with the rational expectations equilibrium model of Veronesi (1999). Intuitively, this means that the informed investor accounts for the probability of a crash but cannot predict when that crash will occur. Additionally, we assume that the informed investor can observe the conditional level of variance, \({\mathrm{s}}_{2}\).Footnote 7

Derivation of propositions

We compare the objective expected utility of the mean-variance investor who ignores non-normality, with the objective expected utility of the informed mean-variance investor who takes non-normality into account. Our focus is on the objective conditional expected utility as known by the “omniscient being” that observes the true underlying probability distribution. We denote this with the subscript O. We also refer to the subjective expected utility that the investor expects to receive given her conditional expectations of return and risk which may or may not be equal to the objective conditional utility. We assume that we have no parameter uncertainty, no forecasting abilityFootnote 8 and no budget constraint. We assume:

  1. 1.

    Returns are skewed, and volatility is stochastic

  2. 2.

    The investor has mean-variance utility

  3. 3.

    The uninformed investor assumes the mean is non-stochastic: \({var(s}_{1})=0\)

  4. 4.

    The uninformed investor assumes volatility is non-stochastic: \({var(s}_{2})=0\) and sets \({s}_{2}=1\)

  5. 5.

    The informed investor is aware that the overall mean is stochastic: \({var(s}_{1})>0\)

  6. 6.

    The informed investor is aware that volatility is stochastic: \({var(s}_{2})>0\)

  7. 7.

    The informed investor is unaware of the level of the mean in each period.

  8. 8.

    The informed investor conditions on the level of volatility \({s}_{2}\)

The unconditional and subjective investor moments are shown in Table 1.

For the informed investor, returns are skewed and volatility is stochastic under Model 1. The utility function is:

$$\begin{array}{*{20}{c}} {{\omega^\prime }\mu - \lambda {\omega^\prime }\Omega \omega \;/2} \end{array}$$
(3)

The optimal weights are given by

$$\begin{array}{*{20}{c}} {\hat \omega = \frac{{{\Omega^{ - 1}}\mu }}{\lambda } = \frac{{{{\left( {\mu \mu ^{\prime}Var\left( {s_1} \right) + {s_2}\Sigma } \right)}^{ - 1}}\mu }}{\lambda }} \end{array}$$
(4)

Substituting the optimal weight of the informed investor into the expected utility function gives the following:

Proposition 1

The unconditional expected mean-variance utility of the informed mean-variance investor under the assumptions of stochastic volatility and skew under Model 1 and where \(\alpha = {\mu^\prime }{\Omega^{ - 1}}\mu\) is given by

$${E_O}\left[ {U_I} \right] = {E_I}\left[ {U_I} \right] = \frac{\alpha }{2\lambda }\left( {E\left[ {\frac{1}{{{s_2} + Var\left( {s_1} \right)\alpha }}} \right]} \right)$$
(5)

Proof: See “Appendix A”

For the uninformed investor, returns are skewed and volatility is stochastic under Model 1

The optimal weights of the uninformed investor are again given by

$$w = \frac{{{\Sigma^{ - 1}}\mu }}{\lambda }$$

The conditional expected return of the uninformed investor is given by

$${E_O}[{r_p}|{s_1}\;] = \frac{{{s_1}{\mu^\prime }{\Sigma^{ - 1}}\mu }}{\lambda }$$

The conditional expected risk is then:

$$\begin{aligned} {E_O}\left[ {\sigma_p^2|{s_1},{s_2}} \right] = & {\omega^\prime }\;\Omega \omega \\ = & \frac{1}{{\lambda^2}}{\left( {{\Sigma^{ - 1}}\mu } \right)^\prime }\left( {Var\left( {s_1} \right)\mu {\mu^\prime } + {s_2}\Sigma } \right)\left( {{\Sigma^{ - 1}}\mu } \right) \\ = & \frac{1}{{\lambda^2}}\left( {{s_2}\alpha + Var\left( {s_1} \right){\alpha^2}} \right) \\ \end{aligned}$$

The expected utility of the uninformed investor is hence given by

$${E_O}\left[ {{U_U}|{s_1},{s_2}} \right] = \left( {\frac{{{s_1}{\upalpha }}}{\lambda } - \frac{1}{{2{\uplambda }}}\left( {{s_2}{\upalpha } + Var\left( {s_1} \right){\alpha^2}} \right)} \right)$$

Now, since \({E_O}\left[ {s_1} \right] = 1\) and \({E_O}\left[ {s_2} \right] = 1\), we have:

Proposition 2

The unconditional expected mean-variance utility of the uninformed mean-variance investor under the assumptions of stochastic volatility and skew under Model 1

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {1 - Var\left( {s_1} \right)\alpha } \right)} \end{array}$$
(6)

It is again clear that this is less than the subjective expected utility. The gain in utility is given by:

$${E_O}\left[ {U_I} \right] - {E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {\left( {{E_O}\left[ {\frac{1}{{{s_2} + Var\left( {s_1} \right)\alpha }}} \right]} \right) - \left( {1 - Var\left( {s_1} \right)\alpha } \right)} \right)$$

Now from Jensen’s inequality, we know

$$\frac{\alpha }{2\lambda }\left( {\left( {{E_O}\left[ {\frac{1}{{{s_2} + Var\left( {s_1} \right)\alpha }}} \right]} \right)} \right) > \frac{\alpha }{2\lambda }\left( {\frac{1}{{1 + Var\left( {s_1} \right)\alpha }}} \right)$$

Hence,

$${E_O}\left[ {U_I} \right] - {E_O}\left[ {U_U} \right] > \frac{\alpha }{2\lambda }\left( {\left( {\frac{1}{{1 + Var\left( {s_1} \right)\alpha }}} \right) - \left( {1 - Var\left( {s_1} \right)\alpha } \right)} \right) > 0$$

The effect of skew and stochastic volatility under Model 2

We now turn to our second model where conditional returns are positively related to conditional variance, and the size of the crash depends on the prevailing level of volatility. Rewriting, for convenience:

$$Model\;2:\quad \;{r_t} = s_2^{1/2}\left( {{s_1}\mu + H{z_t}} \right)$$

The objective conditional mean-variance utility functions for our second model are given by:

$$\begin{array}{*{20}{c}} {{E_O}\left[ {{U_I}|{s_1},{s_2}} \right] = {\omega^\prime }\mu {s_1}s_2^{1/2} - \;\frac{{\lambda {s_2}}}{2}{\omega^\prime }\;\left( {\mu \mu ^{\prime}Var\left( {s_1} \right) + \Sigma } \right)\omega } \end{array}$$
(7)

where \(\lambda\) is the risk aversion parameter, and, as before, the subscript “O” refers to the expectation of the “omniscient being”, with full information.

As in Model 1, the expected values of the two state variables are \({E_O}\left[ {s_1} \right] = {E_O}\left[ {s_2} \right] = 1\) and the two state variables are independent, implying that \({E_O}\left[ {{s_1}{s_2}} \right] = 1\). As well as capturing the characteristics of market behaviour, this approach yields convenient mathematical properties. The objective mean return is determined by the interaction of the two state variables as follows:

$${E_O}\left[ {r|{s_1},{s_2}} \right] = {s_1}s_2^{1/2}\mu$$

The objective conditional covariance matrix is defined as follows

$${\Omega_s} = Cov\left[ {{r_t}|{s_1},{s_2}} \right] = {s_2}\left( {\mu \mu ^{\prime}Var\left( {s_1} \right) + \Sigma } \right)$$

Assuming that the elements of \(\mu\) are positive, the first state variable increases each element of the covariance matrix due to the effect of stochastic mean returns, while the second state variable scales the resulting covariance matrix. Under this model, the informed investor is aware that mean returns are stochastic and that volatility is also stochastic. Again, the informed investor is unaware of the value of the state variable \({s}_{1}\). The informed investor is unaware that the true mean return is a function of the second state variable \({s}_{2}\). Again, the informed investor can condition volatility on \({s}_{2}\) and thus can forecast the future level of volatility without error. The uninformed investor uses the Gaussian i.i.d. assumption.

The unconditional and conditional moments of the investors are shown in Table 2:

Table 2 Unconditional and conditional moments under Model 2 with skew and stochastic volatility
Full size table

For informed investors, returns are skewed and volatility is stochastic under Model 2.

Model 2

The conditional expected return of the informed investor is given by:

$${E_I}\left[ {r|{s_2}} \right] = s_2^{1/2}\mu$$

The informed covariance matrix is defined as follows:

$${E_I}\left[ {\Omega |{s_2}} \right] = {s_2}\left( {\mu {\mu^\prime }Var\left( {s_1} \right) + \Sigma } \right)\;$$

The optimal weights are then given by:

$$\hat \omega = \frac{{{{\left( {\mu \mu ^{\prime}Var\left( {s_1} \right) + \Sigma } \right)}^{ - 1}}\mu }}{{s_2^{1/2}\lambda }}$$

Substituting the optimal weights of the informed investor into the objective utility function gives:

Proposition 3

The unconditional expected mean-variance utility of the informed mean-variance investor under the assumptions of stochastic volatility and skew under Model 2

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_I} \right] = {E_I}\left[ {U_I} \right] = \frac{\alpha }{2\lambda }\left( {\frac{1}{{1 + Var\left( {s_1} \right)\alpha }}} \right)} \end{array}$$
(8)

For the uninformed investor, returns are skewed and volatility is stochastic in Model 2.

The full results are derived in Appendix B. Substituting the weights of the uninformed investor as before into the objective utility function gives:

Proposition 4

The unconditional expected mean-variance utility of the uninformed mean-variance investor under the assumptions of non-stochastic volatility and skew under Model 2

$${E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {2{E_O}\left[ {s_2^{1/2}} \right] - \left( {1 + Var\left( {s_1} \right)\alpha } \right)} \right)$$
(9)

It is easily seen that this is less than the subjective expected utility as \(s_2^{1/2}\) is a concave function so

\({E_O}\left[ {s_2^{1/2}} \right] < 1\) as \({E_O}\left[ {s_2} \right] = 1\).

Using Propositions 3 and 4, the gain in utility is given by:

$$\begin{aligned} {E_O}\left[ {U_I} \right] - {E_O}\left[ {U_U} \right] & = \frac{\alpha }{2\lambda }\left( {\frac{1}{{1 + Var\left( {s_1} \right)\alpha }}} \right) - \frac{\alpha }{2\lambda }\left( {2{E_O}\left[ {s_2^{1/2}} \right] - \left( {1 + Var\left( {s_1} \right)\alpha } \right)} \right) \\ & = \frac{\alpha }{2\lambda }\left( {\frac{1}{{1 + Var\left( {s_1} \right)\alpha }} + \left( {1 + Var\left( {s_1} \right)\alpha } \right) - 2{E_O}\left[ {s_2^{1/2}} \right]} \right) \\ & = \frac{\alpha }{2\lambda }\left( {\frac{{1 + {{\left( {1 + Var\left( {s_1} \right)\alpha } \right)}^2}}}{{1 + Var\left( {s_1} \right)\alpha }} - 2{E_O}\left[ {s_2^{1/2}} \right]} \right) \\ \end{aligned}$$
(10)

Taking the first term with the brackets of Eq. (10), we have

$$\frac{{1 + {{\left( {1 + Var\left( {s_1} \right)\alpha } \right)}^2}}}{{1 + Var\left( {s_1} \right)\alpha }} = \frac{1}{{1 + Var\left( {s_1} \right)\alpha }} + \left( {1 + Var\left( {s_1} \right)\alpha } \right)$$

Now,

$$\frac{1}{{1 + Var\left( {s_1} \right)\alpha }} + \left( {1 + Var\left( {s_1} \right)\alpha } \right) > 2$$

and

$$\frac{1}{{1 + Var\left( {s_1} \right)\alpha }} > 1 - Var\left( {s_1} \right)\alpha \quad {\text{as}}\quad 1 > 1 - Var{\left( {s_1} \right)^2}{\alpha^2}$$

Thus, the first term within the brackets of equation (10) is greater than two, and the second term is strictly less than two by Jensen’s inequality and the gain from accounting for non-normality is unambiguously positive under both of our models.

Closed-form expressions for expected utility under non-normality

Modelling the state variables

In order to quantify the gains from accounting for non-normality, we need to model the distributions of the two state variables. For the first state variable, we require a distribution that can accommodate skew and has a mean of one. We use a modified Bernoulli distribution defined as follows

$$\begin{array}{*{20}{c}} {{s_1}\;\ \;a + \left( {b - a} \right)Bernoulli} \end{array}$$
(11)

where the steady-state scaling factor, \(a > 1\), with a probability, p, and a crash scaling factor, \(b < 1\) with probability, \(1 - p\). Multiplying the mean return vector, \(\mu\), by our modified Bernoulli variable creates negative skew and a heavy left tail while leaving the unconditional return unchanged on average. This is a further example of a mean-preserving spread (Rothschild and Stiglitz 1970). The variance of the Bernoulli distribution is given by

$$V\left( {s_1} \right) = {\left( {b - a} \right)^2}\left( {1 - p} \right)p$$

Since the expected value of the second state variable is 1,

$$E({s_1}) = a + \left( {b - a} \right)p = 1$$

and we can express the variance solely in terms of the crash probability, p, and the crash scaling factor, b.

$$\begin{array}{*{20}{c}} {V\left( {s_1} \right) = \frac{1}{p}{{\left( {1 - b} \right)}^2}\left( {1 - p} \right)} \end{array}$$
(12)

For a fixed probability, \(1-p\), we can see that the variance of our modified Bernoulli distribution increases as the absolute magnitude of the crash, \(b\), increases.

The second state variable that we use to capture stochastic volatility must be strictly positive to prevent the variance from becoming negative and also have a mean of one to ensure the unconditional variance is unchanged on average. We use the scaled chi-square distribution to capture time-varying volatility. This distribution has the attractive feature that the inverse moment can be calculated which allows for explicit expressions for expected utility. Like the standard chi-square, the scaled chi-square is bounded by zero from below and is generated by summing squared random normal variables, consistent with the calculation of variance. Unlike the standard chi-square, the mean is one for all values of \(k\), corresponding to the steady-state market volatility level. The distribution of \({s_2}\) is given by

$$\begin{array}{*{20}{c}} {{s_2}\;\ \;\frac{{{\chi^2}\left( k \right)}}{k}\;} \end{array}$$
(13)

where \({\chi^2}\) defines a chi-square variable with \(k \geqslant 3\) degrees of freedom. The m-th moment of the distribution is given by:

$$\begin{array}{*{20}{c}} {E\left[ {X^m} \right] = \frac{{{2^m}\Gamma \left( {m + \frac{k}{2}} \right)}}{{{k^m}\Gamma \left( \frac{k}{2} \right)}}\;} \end{array}$$
(14)

The parameter k controls the level of variability in the volatility level, \({s_2}\). As k increases, the variability in the level of volatility approaches zero. The second moment of the scaled chi-square distribution is given by

$$\begin{array}{*{20}{c}} {E\left[ {X^2} \right] = \frac{{4\Gamma \left( {2 + \frac{k}{2}} \right)}}{{{k^2}\Gamma \left( \frac{k}{2} \right)}} = 1 + \frac{2}{k}\;} \end{array}$$
(15)
$$\begin{array}{*{20}{c}} {\operatorname{var} \left( X \right) = \frac{2}{k}} \end{array}$$
(16)

Panel A of Fig. 1 shows the density function of the scaled chi-square distribution for four values of k. Panel B shows the variance of the distribution conditional on k.

Fig. 1
figure 1

Probability density of the scaled chi-square distribution (panel A). Variance of scaled chi-square distribution vs. degrees of freedom, \(k\) (panel B). The left-hand panel shows the probability density function of the scaled chi-square distribution for 4, 8, 12 and 16 degrees of freedom. The right-hand panel shows the variance of the scaled chi-square distribution vs. \(k\) as given in equation 18

Full size image

We also draw upon the inverse moment of our modified chi-square distribution.

$$\begin{array}{*{20}{c}} {E\left[ {{X^{ - 1}}} \right] = \frac{{k\Gamma \left( {\frac{k}{2} - 1} \right)}}{{2\Gamma \left( \frac{k}{2} \right)}} = \frac{k}{k - 2}} \end{array}$$
(17)

We now use our modified Bernoulli and scaled chi-square distributions to give closed-form solutions for the expected gain in utility from accounting for non-normality.

Incorporating stochastic volatility and skew under Model 1

We now look to derive closed-form solutions under Model 1 incorporating skew and stochastic volatility. For the informed investor, it is possible to derive a closed-form solution for expected mean-variance utility for particular distributions of the state variable, \({s_2}\) using the following relationship:

$$\begin{aligned} {E_O}\left[ {U_I} \right] = & \frac{\alpha }{2\lambda }\left( {E\left[ {\frac{1}{{{s_2} + Var\left( {s_1} \right)\alpha }}} \right]} \right) \hfill \\ = & \frac{1}{{2\lambda Var\left( {s_1} \right)}}\left( {E\left[ {\mathop \sum \limits_{j = 0}^\infty {{\left( {\frac{{ - {s_2}}}{{Var\left( {s_1} \right)\alpha }}} \right)}^j}} \right]} \right) \hfill \\ \end{aligned}$$

As far as we are aware, however, it is not possible to derive a closed-form solution for expected utility of the informed investor using the scaled chi-square distribution. Accordingly, in the section “Empirical Application” we use numerical integration to give the expected utility of the informed investor. For the uninformed investor, we substitute the expected variance of the modified Bernoulli distribution into Proposition 2 to derive a closed-form expression for expected utility as follows:

Corollary 1

The unconditional expected mean-variance utility of the uninformed mean-variance investor under the assumptions of stochastic volatility and skew under Model 1 using the expected first moment of the modified Bernoulli distribution is

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {\frac{{p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha }}{p}} \right)} \end{array}$$
(18)

For our second stochastic representation, where risk and return is known, we can provide closed-form solutions for the gain in expected utility for both investors as we now show by substituting the variance of the modified Bernoulli distribution (14) into Proposition 3:

Corollary 2

The unconditional expected mean-variance utility of the informed mean-variance investor under the assumptions of non-stochastic volatility and skew under Model 2 using the expected moments of the scaled chi-square and the modified Bernoulli distribution is:

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_I} \right] = \frac{\alpha }{2\lambda }\left( {\frac{p}{{p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha }}} \right)} \end{array}$$
(19)

Substituting the definition of the kth moment of the scaled chi-square distribution (16) with m=0.5 and the variance of the modified Bernoulli distribution (14) into Proposition 4 gives:

Corollary 3

The unconditional expected mean-variance utility of the uninformed mean-variance investor under the assumptions of non-stochastic volatility and skew under Model 2 using the expected moments of the scaled chi-square and the modified Bernoulli distribution is:

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {\frac{{2\sqrt 2 \Gamma \left( {\frac{k + 1}{2}} \right)}}{{\sqrt k \Gamma \left( \frac{k}{2} \right)}} - \left( {\frac{{p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha }}{p}} \right)} \right)\;} \end{array}$$
(20)

The gain in expected utility is then given by the difference between Corollaries 2 and 3.

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_I} \right] - {E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {\frac{{{p^2} + {{\left( {p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha } \right)}^2}}}{{p\left( {p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha } \right)}} - \frac{{2\sqrt 2 \Gamma \left( {\frac{k + 1}{2}} \right)}}{{\sqrt k \Gamma \left( \frac{k}{2} \right)}}} \right)\;} \end{array}$$
(21)

Again, we see that this is unambiguously nonnegative as the first term within the brackets is strictly greater than or equal to 2 and the second term is strictly less than or equal to 2.

Corollary 4

The unconditional expected mean-variance utility of the informed mean-variance investor under the assumptions of non-stochastic volatility, skew and no estimation error under Model 2 using the expected moments of the modified Bernoulli and scaled chi-square distributions is:

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_I} \right] = \frac{\alpha }{2\lambda }\left( {\frac{p}{{p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha }}} \right)} \end{array}$$
(22)

Corollary 5

The unconditional expected mean-variance utility of the uninformed mean-variance investor under the assumptions of non-stochastic volatility and skew under Model 2 using the expected moments of the modified Bernoulli and scaled chi-square distributions is:

$$\begin{array}{*{20}{c}} {{E_O}\left[ {U_U} \right] = \frac{\alpha }{2\lambda }\left( {\frac{{2\sqrt 2 \Gamma \left( {\frac{k + 1}{2}} \right)}}{{\sqrt k \Gamma \left( \frac{k}{2} \right)}} - \left( {\frac{{p + {{\left( {1 - b} \right)}^2}\left( {1 - p} \right)\alpha }}{p}} \right)} \right)\;} \\ {} \end{array}$$
(23)

Empirical application

Data

In this section, we quantify the gain in expected utility from accounting for non-normality by calibrating our models to empirical data. Now, we have stepped away from the general case, and it is a valid criticism that our results are now subject to the vagaries of the data sets we have employed. To mitigate this risk and the scope for data-mining, we use asset classes that span significant periods of time that are commonly used in the literature. We consider the cases of both an international and a domestic investor. The opportunity set of our international investor is comprised of the MSCI equity indices of the G7 countries, Canada, France, Germany, Italy, Japan, the UK and the USA. To calibrate the two models, we use the MSCI total return indices for the period February 1999 to March 2013. Table 3 provides the sample summary statistics. All of the asset returns are negatively skewed and display excess kurtosis. Using the Jarque–Bera test, we can reject normality for each of the assets at the 1% level. We also reject normality in an average of 28% of overlapping 1,000 day sub-periods. The autocorrelation in the absolute value of returns is large and positive, indicative of heteroskedasticity.

Table 3 G7 MSCI indices summary statistics
Full size table

The investment universe of our domestic investor contains the five value-weighted US sectors using the K.R. French data for the period 1/1983-12/2012. The universe contains all NYSE, AMEX and NASDAQ stocks. Sector definitions are based on the four-digit SIC codes. The 30-year interval spans multiple market regimes including the October 1987 crash, the Russian debt default in and collapse of LTCM in 1998, the Tech bubble and ensuing correction beginning in March, 2001, the Financial Crisis of 2007-8 and the ensuing recovery. Table 4 provides the summary statistics. Again, we can reject the hypothesis of normality at the 1% level for each of the indices.

Table 4 Value-weighted US sectors: summary statistics
Full size table

Modelling the state variables with the method of simulated moments

To quantify the gain in utility from accounting for non-normality, we first need to estimate the parameters of the two return models. We employ the Bernoulli and scaled chi-square distributions for the two state variables; other choices are also valid, as discussed above. Estimating the models allows us to decompose the unconditional distribution into a Gaussian i.i.d. component employed by the uninformed investor and a non-Gaussian component that is employed by the informed investor. The stochastic representations of our two models are given by

$$\begin{gathered} Model\;1:{r_t} = {s_1}\mu + s_2^{1/2}H{z_t} \hfill \\ Model\;2:{r_t} = s_2^{1/2}\left( {{s_1}\mu + H{z_t}} \right) \hfill \\ \end{gathered}$$
(24)

where \({s_1}\) and \({s_2}\) are described in equations (11) and (13).

We require estimates of the parameters, \(\widehat{b}\), and \(\widehat{p}\), for the first state variable, the parameter, \(k\) for the second state variable, the vector \(\widehat{\mu }\) and the upper triangular matrix, \(\widehat{H}\) where \(\widehat{H}\) is the Cholesky decomposition of the covariance matrix of the uninformed investor, \(\widehat{\Sigma }\). By simultaneously estimating the parameters, we can decompose the unconditional distribution into a skew-related component and a standard covariance-related component. It is then strictly true that the unconditional covariance matrix, \(\Omega\), is greater than \(\Sigma\) over all elements. In total, we have \(3+2n+n\left(n-1\right)/2\) terms to estimate. This is a formidable challenge made more difficult by the lack of a closed-form multivariate density function, ruling out standard maximum likelihood estimation. McFadden (1998) introduced the method of simulated moments (MSM) to estimate the parameters of multivariate functions for problems where the density function may be difficult to estimate, and it is this approach that we use here. Prior examples of employing the MSM for fitting return generating distributions in an asset allocation context include Brandt (1999), Ait-Sahalia and Brandt (2001) and Das and Uppal (2004).

We are interested in replicating the non-Gaussian characteristics of our data, and we select the parameters, \(\theta\), to minimise weighted squared deviation between the second, third and fourth simulated and empirical moments as described below in (17). To ensure the covariance structure is also captured, we also employ the cross-moments of order two. The i-th empirical moment is given by the time-series average as follows:

$$\begin{array}{*{20}{c}} {{{\hat m}_{simkT,k}} = \frac{1}{T}\mathop \sum \limits_{t = 1}^T {m_i}\left( {z_t^{emp}} \right),\;\quad i = , \ldots ,{n_m}} \end{array}$$
(25)

where T is the number of data points, \({m_i}\left( . \right)\) is a function that gives the moment of order i, and \(z_t^{emp}\) is the observed return in period t.

The simulated counterpart of (15) is given by

$$\begin{array}{*{20}{c}} {{{\hat m}_{simkT,i}} = \frac{1}{T}\mathop \sum \limits_{t = 1}^{kT} {m_i}\left( {z_t^{sim}\left( \theta \right)} \right),\quad i = , \ldots ,{n_m}} \end{array}$$
(26)

where \(k\ge 1\) is a scaling factor that determines the length of the simulation. We select \(k\) to give 100,000 simulated periods per asset.

The vector of differences between the empirical and simulated moments is then given by

$${g_{s,T}}\left( {\theta ,z_t^{{\text{emp}}}} \right) = {\hat m_{{\text{simkT}}}} - {\hat m_{{\text{simpT}}}}$$

To obtain the optimal values of the parameter vector, \(\theta\), we minimise the error term, \({Q_{k,T}}\left( \theta \right)\), as follows.

$$\begin{array}{*{20}{c}} {\hat{\theta} = \arg \min \;{Q_T}\left( \theta \right) = {g_{s,T}}{{\left( \theta \right)}^{\prime}}W{g_{s,T}}\left( \theta \right)} \end{array}$$
(27)

where W is a covariance matrix that we discuss below.

We perform k-step MSM (Hall 2005) as follows. To obtain an initial estimate of \(\widehat{\theta }\), we minimise the squared differences between the simulated and observed moments with respect to the identity matrix. This of course gives equal weight to each of the moment and cross-moment conditions. We can improve on this result by repeating the minimisation with respect to an optimal weighting matrix \(\widehat{W}\) that provides the smallest asymptotic covariance of the estimator. We can estimate the optimal weighting matrix, \(\widehat{W}\), as the inverse of the estimated asymptotic covariance matrix of the moment conditions using the simulated data series. The most elementary estimator we could construct to capture all of the autocovariance is given by

$$\begin{array}{*{20}{c}} {\hat \Omega \left( {\hat \theta } \right) = {{\hat \Gamma }_0} + \mathop \sum \limits_{i = 1}^{T - 1} \left( {\widehat {\Gamma_i} + \widehat {\Gamma_i^\prime }} \right)\;} \end{array}$$
(28)

where

$$\begin{array}{*{20}{c}} {{{\hat \Gamma }_i} = {T^{ - 1}}\mathop \sum \limits_{T = i + 1}^{T - 1} g\left( {\hat \theta ,z_t^{emp}} \right)g{{\left( {\widehat {\theta ,}z_{t - j}^{emp}} \right)}^\prime }} \end{array}$$
(29)

We follow common practice and use a Newey–West (1987) covariance estimator to weight the autocovariances. The result is a heteroskedasticity and autocovariance consistent (HAC) estimator that is guaranteed to be positive definite and has a single solution. The Newey–West estimator computes the asymptotic covariance matrix as if the moment process is a vector moving average and uses the sample autocovariances up until a given lag, l, as follows.

$$\begin{array}{*{20}{c}} {\hat \Omega = {{\hat \Gamma }_0} + \mathop \sum \limits_{l = 1}^l \frac{l + 1 - i}{{l + 1}}\left( {\widehat {\Gamma_i} + \widehat {\Gamma_i^\prime }} \right)\;} \end{array}$$
(30)

While there are a number of complicated formulae that can be used to calculate the optimal number of lags, l, we satisfy ourselves with the smallest integer that satisfies \(l = {T^{1/4}}\).Footnote 9 The optimal weighting matrix for the rth run (iteration) is then given by

$$\begin{array}{*{20}{c}} {\widehat {W_r} = \hat \Omega_r^{ - 1}\left( {{{\hat \theta }_{r - 1}}} \right)\;} \end{array}$$
(31)

We then solve equation (21) iteratively, updating the optimal weighting covariance, \({\hat W_r}\), using the most recent parameter estimates, \({\hat \theta_{r - 1}}\), until we achieve convergence.

Parameter estimates

The optimal parameters for the two models for the G7 countries and the five value-weighted sector indices are shown in Table 5.

Table 5 Parameter estimates for G7 MSCI indices and value-weighted sectors
Full size table

Both models describe the data well. Using the J test, we cannot reject the hypothesis that the empirical returns are generated by either of the stochastic return models. The correlation coefficients between the observed historical moments and the estimated moments of the simulated models are very high for each model and for each data set. In particular, the variance, covariance and kurtosis terms map on extremely well with the correlation coefficients approaching unity. For the sake of brevity, we do not report the t-statistics comparing the empirical and simulated moments.

Consistent with the high correlation coefficients, t-statistics for the moment conditions exceed the 5% critical value for both of the models. It appears that both models are satisfactory in reproducing the key moments of the two data sets. Further, the parameter estimates appear plausible. For example, in the case of the first model for the G7 MSCI index data, the crash probability is \(1-p=\) 0.38%, and the crash state value is -84.76. If we take the average weekly asset return across the G7 countries of 0.21% and substitute into the stochastic return equation of Model 1, we have a steady-state return of 0.26% per week and a crash return of -17.8% per week occurring once every 263 weeks or 5 years. The standard errors of the estimated crash probabilities, \(\widehat{p}\), are small, particularly for the G7 data set. We recognise, however, that the period used to estimate the models for the G7 MSCI data set included the dot-com crash and the global financial crisis and thus may overstate the long-term crash probability and potentially overstate the benefits of accounting for departures from normality, although the possibility of sharp downward corrections in response to major shocks remains a valid concern.

Expected utility and the effect of non-normality under Model 1

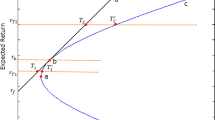
We now use Proposition 1 and Corollary 3 to quantify the gain in expected utility from accounting for non-normality using the first stochastic representation. In Fig. 2, we show the expected utility of the informed and uninformed mean-variance investors conditional on the variability of volatility for three different levels of skew. The horizontal axis shows the variability of the second state variable given by the variance of the scaled chi-square distribution in equation (19). We increase the magnitude of negative skew by increasing the scaling factor, \(b\) while keeping the crash probability constant. The left-hand panel pertains to the G7 MSCI indices, and the right-hand panel pertains to the value-weighted US sectors. In the left panel, we show weekly crash sizes of 0, -8.9% and -17.8%, all at the 0.4% probability level consistent with the best fit parameters in the first column of Table 5. In the right panel, we show weekly crash sizes of 0, -10.6% and -21.2%, at the 0.85% probability level. For the best-fit parameters, we have marked the expected utility of the uninformed and informed investors with a black dot. In each case, we show a zero skew, low skew and high skew case. The high negative skew case in each panel has been selected to correspond with the best fit parameters in Table 5.

Fig. 2
figure 2

Model 1: Expected utility for the informed and uninformed investors for the G7 and US sectors allocation problems. The expected mean-variance utility of the informed and uninformed investors using Proposition 1 and Corollary 3. The left-hand panel relates to the G7 MSCI country indices for the period 2/1999 to 3/2013. The right-hand panel relates to the US value-weighted sectors for the period 1/1983 to 12/2013. The models are calibrated using the method of simulated moments (MSM). We use Monte Carlo simulation to derive the expected values for Proposition 1 and direct substitution for Corollary 3. The parameters used in Proposition 1 and Corollary 3 are given in Table 5. We use a risk aversion \(\lambda =\) 0.05.

Full size image

The effect of increasing the magnitude of negative skew is straightforward, decreasing the expected utility of the informed and uninformed investors. The loss in expected utility is not very large, consistent with Das and Uppal (2004). When volatility is non-stochastic, the expected utility of the informed investor shifts downwards by more than the expected utility of the uninformed investor, because the informed investor is accounting for the additional component of risk due to extreme events, whereas the uninformed investor is not. The introduction of extreme joint returns increases both the correlation and the variance of the unconditional distribution relative to the naïve expectations of the uninformed investor. A parallel can be drawn with the normal mean-variance mixing family where the variance is comprised of a standard variance component and a component driven by the variance in the mean.

The effect of stochastic volatility requires more interpretation. For the informed investor, increasing the level of variability in volatility actually increases expected utility. This is perhaps counter-intuitive and requires more explanation. The reason lies in the convexity of expected utility with respect to volatility. To make this concrete, consider the case of a mean-variance investor with a risk aversion of one in a two-state world investing in a single asset. In the two equally likely states, the variance is equal to 0.5 units in the first state and 1.5 units in the second, and the mean return is 1 unit in both states. The unconditional variance is therefore equal to 1 unit. Assuming that the informed investor can forecast the level of volatility without error, the expected utility is 1 in the first state and 0.33 in the second giving an unconditional expected utility of 0.66. If volatility is non-stochastic, it is easily seen through the standard relation

$$\begin{array}{*{20}{c}} {E\left[ U \right] = \frac{{{\mu^\prime }{\Sigma^{ - 1}}\mu }}{2\lambda }} \end{array}$$
(32)

that the expected utility equals 0.5. Thus, the informed investor gains more when volatility is low than she loses when volatility is high and, paradoxically, a departure from Gaussian i.i.d. returns leads to an increase in expected utility over the non-stochastic case. This is perhaps an unexpected result and an under-appreciated source of utility. For the uninformed investor, the objective expected utility in state one is 0.75 and 0.25 in state two, giving an unconditional expected utility of 0.5 units. The reason the uninformed investor underperforms the informed investor in the presence of non-stochastic volatility is more intuitive. The investor takes too little risk when risk is low and too much risk when risk is high. Put another way, in a world where you can model and account for changes in risk, stochastic volatility represents an opportunity.

The gain in expected utility from accounting for non-normality is given by the vertical distance between the black dots in each panel. For the international investor, the gain in expected mean-variance utility is approximately 3 bps per week, or crudely 1.5% per year. For the domestic investor, the gain is approximately 1.25 bps per week, or 0.65% per year. It is common in the practitioner literature to equate the gain in certainty equivalence to the incremental fee the asset manager could charge by applying a given technique. Malkiel (2013) finds that the average mutual fund fees are approximately 0.9%.Footnote 10 In this context, a gain in certainty equivalence of 0.65% to 1.5% per year is significant. A potential criticism of quantifying the gains in this way is that the gain in expected utility is a function of risk aversion which we have had to estimate. To break the link between the level of risk aversion and the benefits of accounting for non-normality, we consider the percentage gain in expected utility. Dividing Corollary 4 by Proposition 1, we can see that the percentage gain in expected utility is independent of the level of risk aversion. The percentage gain in utility is approximately 38% for the international investor, and 44% for the domestic investor. The majority of the uplift in each case comes from accounting for stochastic volatility. This is a highly significant uplift suggesting that investors should account for non-normality.

Expected utility and the effect of non-normality under Model 2

In Fig. 3, we show the expected utility of the informed and uninformed investors using corollaries 6 and 7, for the second stochastic representation. While in the first model, mean returns and covariance are independent, in the second model, the return vector and the covariance matrix move in lock-step.

Fig. 3
figure 3

Model 2: Expected utility for the informed and uninformed investors for the G7 asset allocation problem. The expected mean-variance utility of the informed and uninformed investors using corollaries 6 and 7. The left-hand panel relates to the G7 MSCI country indices for the period 2/1999 to 3/2013. The right-hand panel relates to the US value-weighted sectors for the period 1/1983 to 12/2012. The models are calibrated using the method of simulated moments (MSM). The parameters used in corollaries 6 and 7 are given in Table 5.

Full size image

As in Model 1, the introduction of skew leads to a decrease in the expected utility for both the informed and the uninformed investors; the uninformed investor experiences a larger decrease in expected utility than the informed investor. In contrast to Fig. 2, as the variability in volatility increases moving left to right, the expected utility of the informed investor remains constant. This is because when volatility is high (low), exposure is low (high) coinciding with when expected returns are high (low). Thus, the investor is not able to exploit low volatility periods and benefit from the variability in volatility in the same way as under our first model. What about the uninformed investor? Increasing the variability in volatility in this case leads to a decrease in expected utility. Whether volatility is above or below the steady-state level, the utility of the uninformed investor is less than the utility of the informed investor. Again, we have highlighted the expected utility for the informed and uninformed investors for the optimal MSM estimates with black dots. For the international investor, the gain in expected utility is approximately 1.3 bps per week, or 0.7% per year. In percentage terms, this translates to a gain of 15%. For the domestic investor, the gain is approximately 0.6 bps per week, or 0.30% per year. The percentage gain for the domestic investor, however, is higher at 25%. Again, the majority of the utility gain comes from accounting for stochastic volatility. Under both our models, whether mean returns are independent of volatility or not, there are economically significant gains from accounting for both stochastic volatility and skew. The gains, however, are more pronounced in the first model where conditional mean returns and conditional variance are independent. This makes sense in that the informed investor can benefit during low volatility periods by scaling up portfolio weights and capturing higher returns. Given the lack of clear empirical evidence showing that conditional mean returns are positively related to conditional variance, it could be argued that the conclusions of our first model should carry more weight.

Conclusion

In this paper, we believe we have been the first to analytically quantify the economic gains that can be captured by the mean-variance investor from accounting both for the skew and stochastic volatility known to be present in asset returns. These gains are economically significant, commensurate with typical mutual fund management fees. The percentage uplift in certainty equivalent is also highly significant at approximately 40%. While accounting for skew is important, the majority of the gains are due to accounting for non-stochastic volatility. This finding aligns with the empirical work of Fleming et al. (2001, 2003), Kirby, and Ostdiek (2012), Gomes (2007) and Han (2006) on volatility timing and the mutual fund work of Busse (1999). The utility gains from incorporating the effect of stochastic volatility into the asset allocation decision are perhaps under-appreciated. In particular, if expected mean returns and volatility are independent, we show that the expected utility of the informed investor actually exceeds the expected utility of the mean-variance investor when returns are non-stochastic. Thus, paradoxically, violations of the i.i.d. Gaussian assumption can increase expected utility relative to the non-stochastic case. This finding also provides theoretical support for the use of conditional volatility models including exponentially weighted moving averages, option implied volatility and GARCH models for portfolio construction. The mean-variance approximation is ubiquitous in the finance industry today and often goes unquestioned by practitioners.