Introduction

Rational investment behavior is one of the most fundamental propositions in standard financial theory. However, the understanding of investment behavior remains incomplete when few behavioral biases rooted in the mind of investors in the real market settings are totally ignored from the consideration. In recent years, finance researchers have increasingly focused on different behavioral issues, and herd behavior is one of them. While stock markets denote a prevalent setting for testing many of the hypothesized effects of behavioral-biased investment activities, little research has been undertaken in the context of the cryptocurrency market. This research offers a detailed analysis of the herding nature and its deviation in different states and frequency data in the cryptocurrency market.

Christie and Huang (1995) first use a cross-sectional standard deviation (CSSD) as the main variable that can explain herd behavior. Later there are numerous studies reported on this behavioral issue in different financial markets (see Choe et al. 1999; Hwang and Salmon 2004; Chiang and Zheng 2010). In a recent paper, Vidal-Tomás et al. (2019) report the traces of herd tendency in the cryptocurrency market. They reveal that small crypto coins are herding with the large coins; hence, crypto investors make their choices on the movement of the leading cryptocurrencies. According to them, Bitcoin is not solely responsible for this market trend, since the rest of the market is not herding with this crypto coin. Current research is conducted by Silva et al. (2019) which demonstrates the presence of herding in the cryptocurrency market. Stavroyiannis and Babalos (2019) also show herding evidence in the cryptocurrency market by using the time-varying parameter regression model.

In this paper, we offer an in-depth study on the herding propensity of the crypto coin market in different states and frequency data. This article is fundamentally different from previous researches in the sense that we analyze herding behavior on different terms of return (short, medium, and long) and different time horizons (high EPU, low EPU, high VIX, low VIX periods). The results show that the nature and scale of herding in the short run are not the same as the nature and scale of herding in the long and medium run. In the same way, herding in the high EPU (Economic Policy Uncertainty) and VIX (CBOE Volatility Index) states is not the same as low EPU and VIX states. The extent of investors' herding level is not the same in different quintiles of return dispersions. In this paper, we also show the herding effect on the next day's coin market returns in various market situations.

Over the past few years, researchers have mainly focused on Bitcoin and used diverse approaches to analyze its investment pattern, performance, and forecasting technique (see Urquhart 2016; Chaim and Laurini, 2018; Grobys et al., 2020), etc. Apart from these, there are quite a good number of papers that have been published on a few major cryptocurrencies like Ethereum, Litecoin, etc. (also see Caporale et al. 2018; Yi et al. 2018). However, there are quite a few numbers of papers that address the cryptocurrency market as a whole. Since the number of market participants is increasing in the cryptocurrency market due to its low-cost and easy transaction features, more research on this market is essential to explore the nature and behavior of crypto coin investors. From the innate quality of a human, investors invest based on their peer decisions. It is not surprising that the coin prices may deviate from their underlying fundamentals.

Herding is observed when investors imitate other market participants instead of using their own judgment. This behavior may sometimes be individually rational, meaning that investors may think they have lesser information than a group of other investors (Avery and Zemsky 1998). Conversely, herd behavior may be irrational when investors over or underprice securities by imitating the wrong decision of their peers. In the crypto coin market, herd behavior may exist in both forms, but it is difficult to segregate this behavior at this point. Empirical works on herding are mainly divided into two main strands. The first stand is the use of investor-specific data to check the herding related with the institutional investors where there is evidence of correlation among investment activities (see Wermers 1999). The second one is researchers use aggregate market data to find out the correlation of markets for the common or similar decision-making pattern of individual investors (Christie and Huang 1995; Galariotis et al. 2015).

We address several empirical questions related to crypto market herding in this paper: is herding behavior significant in the cryptocurrency market? If so, is it significant in different terms of return (short, long, and medium run)? Are there any differences in herding intensity over different states? We also try to solve the question of whether herding exists on the next day's coin market returns in various market situations. Detailed investigation of herd behavior in the cryptocurrency market is important for several reasons. First, it offers a behavioral explanation regarding the reasons for high volatility and extreme market movement observed in the crypto coin prices in certain periods and also its asset pricing implications. Second, since bubbles and crashes are a common phenomenon in this market, herding is something that may intensify these extreme situations. Third, so far most of the cryptocurrency-related research focused on the topics related to the volatility spillover of the major crypto coins (see Zięba et al. 2019; Yi et al. 2018), market efficiency (see Vidal-Tomás et al. 2019; Bariviera 2017), etc.; however, the behavioral aspect of this market is grossly ignored.

In this study, we find the negative and significant squire marker return coefficient in the daily frequency results which indicates the existence of herd behavior in the short run in the cryptocurrency market, though this tendency dies down in the middle and long term. The reason behind this may be for the investors follow the movement of major cryptos in the short run, but later they adjust that price independently according to the merit of that particular crypto. We also find that in the greater uncertainty periods (during the financial crisis periods) herding is more evident than normal or lower uncertainty periods. We observe that there is significant herding exist during the extreme up and down-market condition in case and monthly frequency. We also find that monthly frequency regression shows the traces of herding in the up and down market regression. The rest of the paper proceeds as follows: Section 2 provides the literature review. Section 3 is the data and methods. Section 4 presents the empirical results. Section 5 concludes

Literature review

In this section, this paper discusses two aspects of literature. The first strand is linked with herd behavior which is one of the widely and intensely researched topics within behavioral finance literature, and the second stream of literature is related to the crypto market in general. We also divide this herd-related literature into different asset classes. The first group of literature is related to the herding nature of the stock market; then, we discuss the herding papers related to the other asset classes. Chiang and Zheng (2010) observe herding behavior over a few stock markets. They use data of 18 countries from May 25, 1988, through April 24, 2009, and demonstrate that Asian and advanced markets have traces of herd phenomenon, but there is no evidence of herding in the Latin American market. They also show that the financial crisis induces the tendency of herding in the country of origin and later spread in the neighboring countries. Ina similar way, Chong et al. (2017) explore the reasons behind herd tendency in the Chinese market. They find a significant herding phenomenon in both up and down markets. They demonstrate the effect of speculation, government restrictions, information availability, and systematic risk on the herd behavior of the Chinese stock market. They indicate that herd behavior is not intense for the stocks with high idiosyncratic volatility; instead, it is more prevalent for the stocks with high systematic risk. Chiang et al. (2010) also find a significant herding effect in Shanghai and Shenzhen-A share market but do not get herding evidence in B- share markets. They use quantile regressions to detect the herding tendency of these Chinese stock investors.

Dang and Lin (2016) analyze herd behavior through aggregate market data for stocks where they focus on the nature of random participants with their diverse information. They try to upgrade the tests related to fundamental and non-fundamental herding. Their experimental results reveal within and between-group herding among arbitrageurs and noise traders. Chiang et al. (2013) investigate the herding pattern in the stock market of the pacific basin region. They indicate that herding is time-varying, and it is evident in both bear and bull markets. Mobarek et al. (2014) examine herd behavior on the European developed stock market, and they demonstrate that herding is not evident in the normal time but significant in the extreme market situation. Kudryavtsev (2019) examines the short-run herd behavior on market return. He uses the index data from S&P 500 and uses two different herding measures based on the cross section of daily deviation. He finds that level of herding controls the magnitude of reversal, which is followed by negative and positive market returns. Sarwar (2012) inspects the comparative relationships of the VIX index with stock index returns in BRIC countries (Brazil, Russia, India, and China) and the USA. He claims that a negative and significant contemporaneous relation exists between VIX and the market return of the USA, China, and Brazil. He also finds that a robust negative relationship exists among changes in the VIX index and US market index return, and the relationship intensifies when in the higher volatile VIX periods. Kremer and Nautz (2013) show evidence of herding for institutional herding. They use the database of the German stock market to show the daily herding behavior of institutional investors. They stress that herding is more evident in the largest and highly liquid stocks. Bekiros et al. (2017) investigate the impact of herding on volatility under uncertainty. Their findings claim that in the extreme market situation, herding is more intense than normal conditions. They also show that intense herding is observed at the beginning of a crisis period but dies down at the end.

Hwang and Salmon (2004) advocate a novel method that is based on cross-sectional dispersion related to the factor sensitivity of assets. This approach can give an idea of whether there is a tendency of herding to any sector. They use the US and South Korean stock markets to apply this approach. They demonstrate that macrofactors cannot influence herd behavior; rather, it moves independently regardless of any market conditions. Demirer et al. (2010) detect sector-wise herding evidence in the Taiwanese stock market. They explain the implication for herding behavior and try to explore the source of this herding phenomenon. Lee (2017) examine herd behavior by using a new measure based on cross-sectional co-movement and get a strong signal of herding during mid to large negative price movement but no traces of herding during positive price movement. He uses the weekly stock return of NYSE within the time frame of July 1963 to December 2014. Vo et al. (2017) use daily, weekly, and monthly frequency data to show herding evidence in the Vietnam stock market. They use CSSD approach proposed by Christie and Huang (1995) and CSAD developed by Chang et al. (2000) to show the robust herding behavior in this market. They argue that herding is intense in the down market rather than upmarket in the Vietnam market, and low trading volume days have stronger herding evidence than the high trading volume days. They also demonstrate that herding is more significant in the pre-crisis days rather than post-crisis days. Litimi et al. (2016) reveal that extreme market volatility and bubbles are caused by investors' herding tendency at the US market at the sectoral level. They use the granger causality test to show that herding is the main source for the bubble in a few sectors. Gong and Dai (2017) explain how the interest rate and exchange rate persuade herding in the Chinese stock market. They also indicate that in the idiosyncratic volatility quintile, herding intensity is almost double than the lowest idiosyncratic volatility quintile. This result is consistent with the issue of lottery-like stock where individual investors overprice the extreme positive return generating stocks.

In this section, we discuss the herd-related literature in other asset areas. Clement and Tse (2005) investigate the financial analyst characteristics and herding behavior in forecasting s based on I/B/E/S forecasts of annual earnings from 1989 to 1998. They show that the probability of an analyst's forecast revision is increased with factors like brokerage firm's size, the frequency of forecast, accuracy of the previous analysis, etc. Jiang and Verardo (2018) analyze the connection among herding phenomena in the context of the mutual fund industry. They show that there is a significant negative relationship exists between herd behavior and skill within the mutual fund industry. They demonstrate that funds involved with herding have a significant underperformance than its peer by 2% each year. Jiang and Verardo (2018) focus on the issue of how skill variation may cause differences in herding behavior. They put further light on the adverse association within-herd behavior and future performance of managerial skill. Bahadar et al. (2019) examine the herding behavior related to leveraged exchange-traded funds. They show that in bear LETFs days during daily trading and in crisis periods, herd behavior is more evident. Voukelatos and Verousis (2019) try to relate US market herding with option-implied information. They claim that in general, the US market has no herding tendency, but significant herding exists in the periods with option-implied information, which can demonstrate a negative view of the future prospect of that market. They also indicate that the investor's decisions tend to move toward market consensus during high implied volatility index periods. Avery and Zemsky (1998) show the relationship between asset prices and herd behavior and investigate whether herd tendency consent to an arbitrageur to profitably use the market's learning process. Both individual and institutional investors' positive feedback and herding put an impact on price, and trade as demonstrated by Nofsinger and Sias (1999). They also reveal that institutional herding is positively correlated with the lag return. They also indicate that institutional herding is rational, but there is no evidence of return reversals within two years following the herd periods. Cai et al. (2019) explore that in the case of a corporate bond, institutional herding is much stronger than what is documented, and sell herding is higher and intense than buying herding. They argue that in the corporate bond market institutional investors show significant impact and there has been growing evidence that shows herding and its related price impact in the US corporate bond market

Apart from herding-related literature, there are a few cryptocurrency-related pieces of literature which are needed to be addressed. Nakamoto (2008) first introduces bitcoin as a cryptocurrency by uniting a lot of current ideas from the cypherpunk community. After that, almost 1700 different crypto coins have been registered as cryptocurrency, and day by day, the impact of this market became stronger. Liu et al. (2020) recognize three common risk factors in the cryptocurrency market, which are associated with market return, market capitalization, and momentum. They use both time series and cross-sectional analysis to show the effect of those factors in cryptocurrency return. Zięba et al. (2019) examine the interdependencies among log-returns of crypto coins in the cryptocurrency market. They explore the special topological properties of the cryptocurrency market. In a recent research, Philippas et al. (2020) analyze the effect of informative signals of exogenous factors on the magnitude of herd behavior in the cryptocurrency market. This research provides a unique approach that can endogenize extracted signals. They find considerable asymmetries regarding herding magnitude, which comes from exogenous factors.

Grobys and Sapkota (2019) examine the momentum effect in the cryptocurrency market. Using 143 cryptocurrency price data from 2014 to 2018, they show that cryptocurrency has an insignificant momentum effect and cross-sectional momentum tends to generate negative payoffs that are mostly insignificant. Cheng and Dai (2020) show that the bitcoin price and the related capital inflow volumes of exchange pairs, with high currency conversion profit, respond significantly more positively to carry returns. Katsiampa et al. (2019) demonstrate that cryptocurrency volume is influenced by past information demand flows. They use the VAR model and granger causality test to show the relationship.

Yen and Cheng (2020) examine the relationship between Economic Policy Uncertainty (EPU) with cryptocurrency volatility. They find that the relationship between Economic Policy Uncertainty (EPU) and cryptocurrency volatility is negative and significant. They claim that the ban of cryptocurrency trading by the Chinese government cannot have a significant impact on the predicting power of Chinese EPU over cryptocurrency return volatility. Grobys et al. (2020) show that a simple moving average technique can generate a positive return in the cryptocurrency market. They show that the excess return of 8.76% can be earned from the cryptocurrency market, excluding Bitcoin. Chaim and Laurini (2018) examine the volatility and return jumps in bitcoin data. They reveal that a sudden massive swing of price may be accountable for high unconditional volatility in the cryptocurrency market.

Data and methodology

In this paper, the cryptocurrency price and market capitalization data of the top 200 cryptocurrencies are downloaded from https://coinmarketcap.com/. The Economic Policy Uncertainty (EPU) Index and Chicago Board Options Exchange's (CBOE) Volatility Index (VIX) are downloaded from EPU ( https://www.policyuncertainty.com/us_monthly.html) and yahoo finance web page (https://finance.yahoo.com/quote/%5EVIX/ ), respectively. We rank 200 cryptocurrencies based on the market capitalization of January 1, 2020. We consider 200 cryptocurrencies by following Yi et al. (2018). Many researchers use the top 5–10 cryptocurrencies since these major coins have the majority of market capitalization (see Ji et al. 2019; Bouri et al. 2019). However, this research is related to herd behavior where we like to show how small coins follow the big coins and how the overall market moves as a group. Therefore, it is important to consider both big and small coins in these kinds of research. Hence, we consider 200 crypto coins as in 2020, the market value of the top 200 cryptocurrencies reach more than 200 billion USD (see Tavares et al. 2021). To divide high and low EPU and VIX states, we use the median values of these indices.

To detect herd tendency in a financial market, there are largely two approaches that have been used so far. One is the microapproach and the other is the macroapproach. In this paper, we mainly focus on the macro approach of detecting herd behavior in the cryptocurrency market. First, Christie and Huang (1995) introduce cross-sectional squire deviation as a variable that indicates the level of herding in any financial market. After that, Chang et al. (2000) state that in rational asset pricing theory, the relationship between return dispersions and market volatility is a linear function in normal conditions. That means the rise in the absolute market return value induces the dispersion of investors' returns. However, they observed that this linear relationship becomes nonlinear if investors like to make decision-based on aggregate market trend during larger price fluctuation. To capture this nonlinear price movement, they introduce (Rm,t)2 in their regression equation. Hence, the presence of negative significant coefficients indicates the traces of herd behavior in the cryptocurrency market (Tables 1, 2).

Table 1 Top 200 ranked cryptocurrencies (based on market capitalization on January 1, 2020)
Full size table
Table 2 Summary statistics
Full size table

Initially, Christie and Huang (1995) introduce cross-sectional standard deviation of returns (CSSD) as a variable to detect herd behavior in a market setting. The CSSD measure is defined as

$${\text{CSSD}}_{t} = \sqrt {\frac{{\mathop \sum \nolimits_{i}^{N} \left( {R_{i,t} - R_{m,t} } \right)^{2} }}{N - 1}}$$
(1)

where Rm,t is the market return at time t, Return is the return on firm i at time t, N is the number of firms. However, in a later paper, Chang et al. (2000) introduce the cross-sectional absolute deviation of returns (CSAD) as the measure of dispersion where

$${\text{CSAD}}_{t} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {R_{i,t} - R_{m,t} } \right|$$
(2)

Chang et al. (2000) argue that rational asset pricing theory only uses linear equation meaning that equity return dispersions are an increasing function of the market return and it has a linear relation. However, according to Chang et al. (2000), the relationship may nonlinear during the time of large price movement and this relation may be both increasing and decreasing. Chang et al. (2000) use Black (1972) CAPM's conditional version of the equation which can be written as

$$E_{t} (R) = \gamma_{0} + \beta_{i} E_{t} \left( {R_{m} - \gamma_{0} } \right)$$
(3)

where γ0 is the return on zero beta portfolio. βi is the time-invariant systematic risk measure of the security, i = 1…….,N and t = 1,..,T. Also βm is the systematic risk of an equally weighted market portfolio.

$$\beta_{m} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \beta_{i}$$
(4)

The absolute value of the deviation of security i's expected return in period t from the tth period portfolio return which can be

$${\text{ADV}}_{i,t} = \, \left| {\beta_{i} - \, \beta_{m} } \right|E_{i} \left( {R_{m} - \gamma_{0} } \right)$$
(5)

Hence, this can be defined as expected cross-sectional absolute deviation of return (ECSAD) in period t as follows

$${\text{ECSAD}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} {\text{AVD}}_{i,t} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\beta i - \beta m} \right|E_{i} (Rm - \gamma_{0} )$$
(6)

The increasing linear function dispersion and market expected return can be

$$\frac{{\partial E{\text{CSAD}}_{t} }}{{\partial E_{t} \left( {R_{m} } \right)}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\beta i - \beta m} \right| > 0$$
(7)
$$\frac{{\partial E{\text{CSAD}}_{t} }}{{\partial E_{t} \left( {R_{m} } \right)^{2} }} > 0$$
(8)

From the above solution, Chang et al. (2000) introduce nonlinear regression parameter which is mainly used in our paper.

Here, Return is the percentage log daily return which is

$$R_{i,t} = \, 100*\ln \left( {{\text{price}}_{i,t} \left[ {\_n} \right]/{\text{price}}_{i,t} \left[ {\_n - 1} \right]} \right);$$
(9)

the equally weighted market portfolio is used to calculate market returns which is

$${\text{MR}}_{m,t} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} r_{i,t} }}{N},$$
(10)

We use the following equation which is developed by Chang et al. (2000)

$${\text{CSAD}}_{t} = \, \gamma_{0 \, + } \gamma_{1} \left| {R_{m,t} } \right| + \, \gamma_{2} \left( {R_{m,t} } \right)^{2} + \varepsilon$$
(11)

where CSAD is the cross-sectional absolute deviation. Rm,t is the market return at time t. Return is the percentage log daily return which is 100*ln(price[_n]/price[_n−1]). γ0 is the constant, γ1, γ2 are coefficients and εt is the error term at time.

$${\text{CSAD}}_{t} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {R_{i,t} - R_{m,t} } \right|$$
(12)

To capture the herding tendency in the up and down market, we use the following equation in this paper:

$${\text{CSAD}}_{t} = \, \gamma_{0} + \gamma_{1}^{{{\text{up}}}} D^{{{\text{up}}}} \left| {R_{m,t} } \right| + \, \gamma_{2}^{down} D^{{{\text{down}}}} \left( {R_{m,t} } \right)^{2}_{ + } \gamma_{3}^{{{\text{up}}}} D^{{{\text{up}}}} \left| {R_{m,t} } \right| + \, \gamma_{4}^{{{\text{down}}}} D^{{{\text{down}}}} \left( {R_{m,t} } \right)^{2} + \varepsilon_{t}$$
(13)

where Dup = 1 is the dummy variable representing periods with positive market returns and Dup = 0 when the return is negative. The same way, Ddown = 0 is the dummy variable representing periods with positive market returns and Ddown = 0 when the return is negative. γ0 is the constant, γ1up, γ2down, γ3up, γ4down are coefficients, and εt is the error term at time. Herding effects are present if γ3up < 0 and γ4down < 0.

For the extreme upside and downside movement, we use following equation in this paper:

$${\text{CSAD}}_{t} = \, \gamma_{0 \, + } \gamma_{1}^{up} D^{up} \left| {R_{m,t} } \right| + \, \gamma_{2}^{up} D^{up} \left( {R_{m,t} } \right)^{2}_{{}} + \varepsilon$$
(14)

where Dup = 1 if Rm,t > 0 is within the extreme 1%, 5%, and 10% cutoff point in upper tail distribution.

$${\text{CSAD}}_{t} = \, \gamma_{0} + \gamma_{1}^{{{\text{down}}}} D^{{{\text{down}}}} \left| {R_{m,t} } \right| + \, \gamma_{2}^{{{\text{down}}}} D^{{{\text{down}}}} \left( {R_{m,t} } \right)^{2} + \varepsilon$$
(15)

where Ddown = 1 if Rm,t < 0 is within the extreme 1%, 5%, and 10% cutoff point in lower tail distribution. CSAD is the cross-sectional absolute deviation

To capture herding in the low and high Economic Policy Uncertainty (EPU) periods, we use the following equations

$$\begin{aligned} {\text{CSAD}}_{t} & = \, \gamma_{0 \, } + \gamma_{1}^{{{\text{highEPU}}}} D^{{{\text{highEPU}}}} \left| {R_{m,t} } \right| + \, \gamma_{2}^{{{\text{lowEPU}}}} D^{{{\text{lowEPU}}}} \left( {R_{m,t} } \right)^{2} \\ & \quad + \gamma_{3}^{{{\text{highEPU}}}} D^{{{\text{highEPU}}}} \left| {R_{m,t} } \right| + \, \gamma_{4}^{{{\text{lowEPU}}}} D^{{{\text{lowEPU}}}} \left( {R_{m,t} } \right)^{2} + \varepsilon \\ \end{aligned}$$
(16)

where DupEPU = 1 if EPU is higher than its median value and DlowEPU = 1 if EPU is lower than its median value. CSAD is the cross-sectional absolute deviation

For sorting out herding in the low and high CBOE Volatility Index (VIX) periods, we use the following equations:

$$\begin{aligned} {\text{CSAD}}_{t} & = \, \gamma_{0} + \gamma_{1}^{{{\text{highVIX}}}} D^{{{\text{highEPU}}}} \left| {R_{m,t} } \right| + \, \gamma_{2}^{{{\text{lowVIX}}}} D^{{{\text{lowVIX}}}} \left( {R_{m,t} } \right)^{2} \\ & \quad + \gamma_{3}^{{{\text{highVIX}}}} D^{{{\text{highVIX}}}} \left| {R_{m,t} } \right| + \, \gamma_{4}^{{{\text{lowVIX}}}} D^{{{\text{lowVIX}}}} \left( {R_{m,t} } \right)^{2} + \varepsilon \\ \end{aligned}$$
(17)

where DupVIX = 1 if EPU is higher than its median value and DlowVIX = 1 if EPU is lower than its median value. CSAD is the cross-sectional absolute deviation

Results

Cryptocurrency herding in different terms (short, middle, and long)

Table 3 shows the regressing coefficients of Eq. 11 given by Chang et al. (2000). The positive and significant coefficients for absolute market return in daily and monthly frequency declare a significant positive linear relationship between absolute market return and cross-sectional absolute deviation, which is consistent with the conventional asset pricing theories. However, the negative coefficient of absolute return in the weekly frequency result shows market inefficiency in the middle term. On the other hand, the negative and significant squire marker return coefficient in the daily frequency results states the existence of herd behavior in the short run in the cryptocurrency market, though the herd behavior phenomenon dies down in the middle and long term. As Christie and Huang (1995) describe, herding is a short-lived tendency meaning that our results are in line with their notion.

Table 3 Regression results on CSAD
Full size table

At this stage, we do not segregate the fundamental and non-fundamental herd behavior. Hence this herd effect possibly contains both elements. Fundamental herding is the spurious or unintentional herding by investors, which may not be affected by market return or volatility. Using monthly holding data of Portugal, Holmes et al. (2013) tried to show whether the herd behavior that exists in the Portuguese market is spurious or intentional, and they argued that spurious herding should not be affected by market return and volatility. This unintentional herding may be caused by several reasons like the rumor of price hike or fall, homogeneity of investors, the tendency of too much inclination toward cryptocurrency over a certain period, etc.

Many past works of literature indicate that herd tendency is responsible for the price deviation from the asset fundamentals (Hwang and Salmon 2004; Brown et al. 2021). That means herding can induce investors to invest in overpriced or underpriced assets. Hence, it is a rational proposition that in the highly volatile cryptocurrency market, investors have a herding tendency, and they may tend to make market consensus irrationally. Imitating other behavior in the cryptocurrency market may both be rational and spurious. If a large number of market participants believe that the other participants are better informed than themselves, following others' actions in this context may be rational. However, this belief, right or wrong maybe and investors may experience negative or positive outcomes based on the correctness of that belief (Figs. 1, 2 and 3).

Fig. 1
figure 1

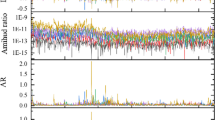
Cross-sectional absolute deviation (CSAD) from 2013 to2020. Note: This figure plots cross-sectional absolute deviation (CSAD) of daily stock return from July 2013 to January 2020. CSADt = \(\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \left| {R_{i,t} - R_{m,t} } \right|\) where Rm,t is the market return at time t. Return is the percentage log return which is 100*ln(price[_n]/price[_n−1])

Full size image
Fig. 2
figure 2

Cross-sectional squire deviation (CSSD) from 2013 to2020. Note: This figure plots cross-sectional squire deviation (CSSD) of daily stock return from July 2013 to January 2020. CSSDt = \(\sqrt {\frac{{\mathop \sum \nolimits_{i}^{N} \left( {R_{i,t} - R_{m,t} } \right)^{2} }}{N - 1}}\). where Rm,t is the market return at time t. Return is the percentage log return which is 100*ln(price[_n]/price[_n−1])

Full size image
Fig. 3
figure 3

Cross-sectional absolute deviation (CSSD) and market return from 2013 to2020. Note: This figure plots cross-sectional absolute deviation (CSAD) of daily stock return from July 2013 to January 2020 with respect market return in the horizontal axis. CSADt = \(\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \left| {R_{i,t} - R_{m,t} } \right|\) where Rm,t is the market return at time t. Return is the percentage log return which is 100*ln(price[_n]/price[_n−1])

Full size image

Cryptocurrency herding in the up and down market

Table 4 indicates that there is significant herding exist during the down-market condition in the case of both daily and monthly frequency. Herding behavior also remains in the monthly frequency during the upmarket. Herd during the financial crisis is more evident than normal or better economic conditions. History shows that just after big financial distress, investors tend to herd in the financial markets. Hence, herding evidence in the long run during the financial crisis periods is not surprising. Mobarek et al. (2014) show significant herding evidence and asymmetric market condition for the period of 2001–2012 within a few developed European countries. That means European markets do not have a herding tendency in the normal market situations, but during distressed market conditions, they are inclined to mimic other participants. Gleason et al. (2004) also mention that during the higher financial stress period, investors try to relieve through market consensus. In their opinion, this kind of herding may be a low-cost solution for highly expensive sophisticated information.

Table 4 Regression results for up and down market
Full size table

Cryptocurrency herding in the extreme up and down market

Christie and Huang (1995) indicate that during the extreme market condition, herding would be more prevalent. Many fresh shreds of evidence suggest that there is an occurrence of extreme market movements in crisis periods. However, the existence of extreme market movement is also visible in better market conditions. Chiang and Zheng (2010) show that investors in Mexico and Argentina tend to herd when a crisis comes into their market. They also argue that investors may herd with their neighbor countries, and they show that Argentinean investors herd with Mexican investors in the 1994–1995 financial crisis. Brazil also herds with Argentina in the 1999 crisis state. In the cryptocurrency market, we find that market asymmetry is only observed in the extreme upmarket in the long run. In Table 5, the results of the upmarket coefficient with squire market return (γ2up) from monthly frequency produce a negative value − .145 with a t statistic of − 22.04, meaning that there is evidence of herd activity during extreme upmarket in the long run. In the case of other frequencies, we do not find any traces of herd activity from investors during extreme market movement periods (Table 6).

Table 5 Extreme upside market movement
Full size table
Table 6 Extreme downside market movement
Full size table

This result is unique in the sense that in most financial markets, heavy herd behavior is observed during extreme market conditions. For example, Vo et al. (2017) show that in extreme market conditions, Vietnam stock traders cluster around the market consensus. They also indicate that herd behavior is a short and middle terms phenomenon for the Vietnam market, and there is no evidence that supports the existence of herd behavior in the long run. Hence the nature of herding behavior in the cryptocurrency market is noticeably different than Vo and Phan's (2017) evidence. Bekiros et al. (2017) also show that in the US market, herding magnifies during the extreme market condition. They argue that substantial herding exists at the beginning of a crisis period, but it dies down in the end.

Quintile regression

The quintile approach of herding analysis is effective because it provides the different herding magnitude with the condition of a certain group of data. Hence, in this section, we address the herding behavior in different quintiles of return dispersion. Buchinsky (1998) indicates that quintile coefficients may provide better estimation than the ordinary least squire technique if the error distribution is not able to conform to a Gaussian setting. Since in the cryptocurrency market, extreme values can effectively disturb the tail values of the return distribution, there is a possibility that ordinary least squire estimation can produce distorted results. Therefore, we provide results in three different quintiles in Table 7. It shows that the herding phenomenon is more prevalent in the higher quintiles of return dispersions in the short run. The quadratic return coefficient (γ2) is negative and significant in both cases (τ = .50 and τ = .75) in the daily frequency results. However, in line with our main result, herding behavior is not evident in the middle and long term in the cryptocurrency market.

Table 7 CSAD quantile regression
Full size table

Herding in the high and low economic policy uncertainty states

Philippas et al. (2020) show that cryptocurrency herding is influenced by various kinds of external signals. Economic Policy Uncertainty is one of the major sources of signal that may induce herding behavior in the cryptocurrency market. This index is introduced by Baker et al. (2016), and investors in the cryptocurrency market may use EPU index information to predict the future movement of the cryptocurrency market. Investors, both individual and institutional, are somewhat influenced by different government policy implications such as monetary or fiscal policy, trade rules, tax benefits, etc. According to Baker et al. (2016), the uncertainty related to government policy decisions greatly influences the economy and financial markets.

EPU causes investors to reshuffle and changes their portfolio combination to avoid potential wealth loss. In Table 8, we find traces of higher herding behavior in the daily frequency data in low uncertainty periods, but in the monthly frequency data or in the long run, the herding behavior is observed in high uncertainty periods. That means in the short run; investors feel comfort to herd when uncertainty remains low. But in the long run, investors tend to herd in the high uncertainty periods. However, in the middle run, we do not find any herding tendency in both periods. The result is somewhat interesting because it demonstrates that the pattern of herding is not the same in different uncertainty states.

Table 8 Herding low versus high economic policy uncertainty (EPU) periods
Full size table

Herding in the high and low VIX States

The market volatility index (VIX) is a popular indicator that demonstrates investors' fear gauges in different financial markets. A high VIX value indicates the possibility of high fluctuations in financial asset values. This index is also called the CBOE Volatility Index (VIX) because the index is compiled by the Chicago Board Options Exchange (CBOE). Giot (2005) claims that after a high level of VXO (old VIX) there are traces of high return indicates that VXO has a predictive capacity regarding the future return. The market return is positively related to implied volatility revealed by Guo and Savickas (2006). Dash and Moran (2005) demonstrate that hedge fund return and VXO are negatively correlated with each other. Akyildirim et al. (2019) indicate that there is evidence of substantial correlations remains within cryptocurrency volatility and volatility indices like VIX. Moreover, the GARCH-calculated volatility of cryptocurrencies is higher in the highest deciles of implied volatility.

In Table 9, the result indicates that both in daily and monthly frequency data hard behavior is evident during low VIX periods meaning that investors tend to involve herding when they have less fear of future volatility. Previous evidence shows that herding itself may be a cause of increasing future volatility in the stock markets. Blasco et al. (2012) claim that herding variables are suitable for volatility forecasting and consequently in the decision-making process when volatility is considered as a key factor. This result is indicating that investors are reluctant to herd in the cryptocurrency market when they have the fear of high future price deviation.

Table 9 Herding low versus high VIX periods
Full size table

Herding effect on the next day's market returns

This section shows the predictability of cryptocurrency returns based on the prior day's cross-sectional market-wide herding tendency. Here the assumption is that herding may induce the price overreaction, and it may lead to price reversal in the following day meaning that the magnitude of market returns may be higher (lower) based on the previous trading day's negative (positive) market returns and also with the level of herding. The results of this section (Tables 10, 11, and 12) demonstrate that how the market-wide levels of herding influence the magnitude of price reversal where [MR(− 1) > 0] is the positive lag market return and [MR(− 1) < 0] is the lag negative market return. CSAD (− 1) is the lag cross-sectional absolute deviation and CSSD (-1) is the lag.

Table 10 Herding effect on the next day's cryptocurrency market returns: full sample
Full size table
Table 11 Herding effect on the next day's cryptocurrency market returns: bull market
Full size table
Table 12 Herding effect on the next day's cryptocurrency market returns: bear market
Full size table

In Table 8, if the previous day's market return is positive [MR(− 1) > 0], then the current day's average market return equals is lower in the low CSAD and CSSD group than the high CSAD and CSSD. The return difference between high CSAD and CSSD market return and low CSAD and CSSD market return is positive and statistically significant. The negative significant return difference between high CSAD and CSSD market return and low CSAD and CSSD market return is observed when the previous day's market return is negative [MR(− 1) < 0]. In both cases, the significant return difference indicates the impact of herding in different market conditions on return. Similarly, Tables 11 and 12 show the impact of different levels of herding on market return in bull and bear markets, respectively. In all cases, the market return difference is significant meaning that due to different level of herding the magnitude and nature of market return reversal are different.

Conclusion

Here we provide an in-depth analysis on herding propensity in the cryptocurrency market in different states and frequency data. The results clearly indicate that the nature and magnitude of herding in the short-run (daily frequency) are not similar to the nature and magnitude of herding in the long and medium run (monthly and weekly frequency, respectively). We show that herding in the high EPU (Economic Policy Uncertainty) and VIX (CBOE Volatility Index) states is not the same as low EPU and VIX states. In the same way, the magnitude of investors' imitation of predecessors' decisions is not identical in different quintiles of return dispersions. In this paper, we also show the herding effect on the next day's coin market returns in numerous market conditions.

Though the cryptocurrency market is a highly speculative market, the amount of research on herding in this market is very limited. Hence, this paper will mitigate this research gap and can provide a clear idea of the herding nature of the cryptocurrency market. In a recent paper, Vidal-Tomás et al. (2019) first show the traces of the herding phenomenon in the cryptocurrency market. Silva et al. (2019) also examine both the herding and contagion effect in the cryptocurrency market. However, we examine herd behavior in the cryptocurrency market by using different states and frequency data-keeping major 200 crypto coins in our samples. We mainly use CSAD (developed by Chang et al. 2000) approaches to show herd tendency in this paper.

We find the negative and significant squire marker return coefficient in the daily frequency results which indicates the existence of herd behavior in the short run in the cryptocurrency market, though this tendency dies down in the middle and long term. The reason behind this may be for the investors follow the movement of major cryptos in the short run, but later they adjust that price independently according to the merit of that particular crypto. We also find that in the greater uncertainty periods (during the financial crisis periods) herding is more evident than normal or lower uncertainty periods. We observe that there is significant herding exist during the down-market condition in the case of both daily and monthly frequency. We think that individual investors, managers, and policymakers can use the results in different parts of their decision-making process related to the cryptocurrency market. Since herding is an inherent nature of all human beings, this phenomenon cannot be ignored in real investment settings. Therefore, in-depth knowledge of the nature of herding in any market is important to take correct investment and policy decisions. We believe that this paper has a significant impact in this regard.