Pricing ambiguity in catastrophe risk insurance

Abstract

Ambiguity about the probability of loss is a salient feature of catastrophe risk insurance. Evidence shows that insurers charge higher premiums under ambiguity, but that they rely on simple heuristics to do so, rather than being able to turn to pricing tools that formally link ambiguity with the insurer’s underlying economic objective. In this paper, we apply an $\alpha$-maxmin model of insurance pricing to two catastrophe model data sets relating to hurricane risk. The pricing model considers an insurer who maximises expected profit, but is sensitive to how ambiguity affects its risk of ruin. We estimate ambiguity loads and show how these depend on the insurer’s attitude to ambiguity, $\alpha$. We also compare these results with those derived from applying model blending techniques that have recently gained popularity in the actuarial profession, and show that model blending can imply relatively low aversion to ambiguity, possibly ambiguity seeking.

Introduction

Ambiguity, defined as uncertainty about the relative likelihood of events (Ellsberg 1961), is a common feature of insurance (Hogarth and Kunreuther 1989). Ambiguity is particularly likely to affect pricing of catastrophe reinsurance, where historical loss data are limited for higher risk layers.¹ Hurricane risk provides a good motivating example of the issues. A number of insurers and especially reinsurers failed in the aftermath of Hurricane Andrew, which made landfall as a category four hurricane in south Florida in August 1992. They failed principally because they had been relying on loss data from the previous two decades for pricing, reserving and so on (Calder et al. 2012). But 1971–1991 (or thereabouts) was an historically quiet period for Atlantic hurricane activity (Landsea et al. 1996),² as well as being a period during which insured values and insurers’ exposure were changing. Partly as a consequence of Andrew, probabilistic catastrophe models have become widely used in the insurance industry as a means of estimating catastrophe risks. However, while catastrophe models may provide a better basis for estimating catastrophe risk than relying on the historical record alone, such models tend not to provide unambiguous loss probabilities. For example, Mao (2014) recently reported widely differing estimates of insured losses from a 1/250-year Florida hurricane, ranging from $54 billion to $151bn, with the three leading commercial catastrophe model providers disagreeing on both the mean loss and the range. As well as ambiguity, this can be described as a situation of ‘model uncertainty’ (e.g. Marinacci 2015).³

Ambiguity tends to result in higher premiums than those charged for equivalent, unambiguous risks (see Hogarth and Kunreuther 1989, and further references below). Yet, while it is well known that ambiguity contributes to higher insurance premiums and accompanying problems of availability and coverage, the economic rationale for this has received less attention. This is not only true of the academic literature, it is also true of industry practice, where insurance actuaries and underwriters appear to rely on simple rules of thumb to load premiums under ambiguity (Hogarth and Kunreuther 1992). To redress the balance, Dietz and Walker (2019) have recently proposed an $\alpha$-maxmin representation of the insurer’s decision problem under ambiguity. The insurer is assumed to follow a safety-first model, maximising expected profit subject to a survival constraint (Stone 1973). The insurer’s attitude to ambiguity affects the premium through the amount of capital it must hold against the risk of ruin. An ambiguity-averse insurer places more weight on higher probabilities of ruin, therefore holds more capital, and charges a higher capital load on the premium if the new contract increases the probability of ruin.

In this paper, we apply the model of Dietz and Walker (2019) to two data sets, where conflicting catastrophe models create ambiguity about the probability of insured losses. The two data sets both relate to hurricane risk in the Atlantic basin. In one, Florida property, ambiguity stems from a set of hurricane models yielding different estimates of hurricane activity. In the other, Dominica property, we assume a unique estimate of the probability of hurricane activity, but there is nonetheless ambiguity, which stems from different vulnerability functions describing a property portfolio. These applications enable us to demonstrate the practical use of an economic premium principle that treats ambiguity explicitly and thereby quantifies the ambiguity load as a function of the insurer’s attitude to ambiguity. We argue the application of this principle has the capacity to improve on ad hoc adjustments, even if it is unable to avoid the need for them altogether. The second purpose of the paper is to compare the results of this with the premiums that would be quoted by an insurer, who is also an expected profit maximiser operating under a survival constraint, but where the unique probability of loss is derived from the application of model blending techniques popular in the insurance industry. The comparison shows these model blending techniques can imply the insurer has relatively low aversion to ambiguity, possibly seeking ambiguity.

The remainder of the paper is structured as follows. Section 2 reviews related literature underpinning our introductory comments. Section 3 provides a brief analytical treatment of the safety-first model of insurance pricing and Dietz and Walker’s (2019) $\alpha$-maxmin model of reserving under ambiguity, as well as how the risk of ruin is estimated using popular methods of model blending. Section 4 introduces and analyses the two case studies, and Sect. 5 provides a discussion.

Related literature

That ambiguity results in higher premiums than those charged for equivalent, unambiguous risks was a feature of industry practice that was widely suspected, but difficult to isolate from other factors tending to raise premiums. Therefore a series of studies used experimental and survey methods to establish, in controlled conditions, the practice of loading premiums under ambiguity (Hogarth and Kunreuther 1989, 1992; Kunreuther et al. 1993, 1995; Cabantous 2007; Kunreuther and Michel-Kerjan 2009; Cabantous et al. 2011; Aydogan et al. 2019). The participants in these studies, mostly insurance professionals (including actuaries and underwriters), were asked to price hypothetical contracts, with the existence of ambiguity about losses being a treatment. The results consistently showed that higher prices were quoted under ambiguity compared with when a precise probability estimate was available.⁴ This insurer ambiguity aversion is consistent with a broader body of evidence on individual decision-making under ambiguity (reviewed by Machina and Siniscalchi 2014), initiated by Ellsberg’s thought experiments about betting on balls being drawn from urns (Ellsberg 1961).

While it is well known that ambiguity contributes to higher insurance premiums and accompanying problems of availability and coverage, the economic rationale for this has received less attention. Hogarth and Kunreuther (1989) showed that a positive ambiguity load is consistent with a risk-neutral insurer who maximises expected profit, if the insurer’s beliefs about the probability of loss are formed according to the psychological model of Einhorn and Hogarth (1985). In this model, the insurer’s probability estimate is distorted such that, for low-probability events like catastrophe risks, greater weight is placed on higher probabilities of loss. That is, the insurer forms pessimistic beliefs when insuring catastrophe risks. A basic result of decision theory is that expected utility maximisation is inconsistent with ambiguity aversion (Ellsberg 1961). However, Berger and Kunreuther (1994) showed that an ambiguity load could be consistent with a risk-averse insurer who maximises expected utility, if (and only if) the effect of ambiguity is to increase the correlation between risks in the insurer’s portfolio.⁵ They also showed, again under special assumptions about the nature of the ambiguity,⁶ that an ambiguity load is consistent with a safety-first model of an expected-profit-maximising insurer who must satisfy an insolvency/ruin/survival constraint in the tradition of Stone (1973). Moreover they showed that this safety-first model better explains other results in the experimental/survey literature than does the expected utility model. What makes this approach attractive is that survival constraints are widely used in the insurance industry and have become enshrined in some regulations such as the European Union’s Solvency II Directive.

Dietz and Walker (2019) have recently proposed an alternative $\alpha$-maxmin representation of the insurer’s decision problem under ambiguity, which is also based on an expected profit maximiser facing a survival constraint. The insurer’s attitude to ambiguity potentially affects the premium through the amount of capital it chooses to hold against the risk of ruin. An ambiguity-averse insurer places more weight on higher probabilities of ruin, therefore holds more capital, and charges a higher capital load on the premium if the new contract increases the probability of ruin (vice versa for an ambiguity-seeking insurer). This is also a form of pessimism. The advantages of the model in Dietz and Walker (2019) are that it is consistent with ambiguity loading under quite general conditions whereby a new contract increases the ambiguity of the insurer’s portfolio, and that, drawing on recent advances in decision theory (especially Ghirardato et al. 2004, but with ideas going back to Hurwicz 1951), it captures the insurer’s attitude to ambiguity via an easily interpretable parameter, $\alpha$, that is clearly separated from the insurer’s beliefs about the probabilities of loss.

The actuarial literature that directly engages with ambiguity would also appear to be sparse. Two areas are particularly relevant to the current setting. The first is the development of premium principles. In this regard, Pichler (2014) observes that all well-known premium principles assume a unique, stable loss distribution. One or two of these principles take ambiguity into account indirectly through the practice of distorting the loss distribution, placing more weight on higher loss probabilities and therefore introducing pessimistic beliefs like the Einhorn and Hogarth (1985) model. The second is the development of techniques, primarily by practitioners, to mix multiple, conflicting probability estimates into a single estimate that can be inputted into a standard premium principle such as the expected value principle. These have come to be referred to as catastrophe model ‘blending’ (Calder et al. 2012). The interesting feature of these techniques, from our point of view, is that their development has been based on satisfying certain mathematical properties and generally without attention to insurers’ fundamental economic objective.

In view of the relatively limited body of theory on how ambiguity affects insurance supply,⁷ it is perhaps unsurprising that insurance actuaries and underwriters appear to rely on simple rules of thumb in practice when loading premiums under ambiguity. Hogarth and Kunreuther (1992) provided some structured evidence of this from their mail survey of actuaries. A subset of respondents provided written comments giving insight into their decision processes. Most of these responses indicated that actuaries first anchored the premium on the expected loss, and the majority of these would then, when informed the probability of loss was ambiguous, explicitly or implicitly apply an ad hoc adjustment factor or multiplier (e.g. increase the premium by 25%). Anecdotally such practice is widespread.

Pricing insurance

Premium principle

An insurer that seeks to maximise its expected profits subject to a survival constraint would price premiums according to

$$\begin{aligned} p_{c}=L_{c}+y\left( Z_{f'}-Z_{f}\right) , \end{aligned}$$

(1)

where $p_{c}$ is the premium on contract c, $L_{c}$ is the expected loss, y is the cost of capital and $Z_{i}$ represents the insurer’s capital reserves held against portfolio $i\in \left\{ f,f^{\prime }\right\}$.⁸ When the insurer takes on contract c, the insurer’s portfolio is $f^{\prime }=f+c$. Thus expected profit maximisation implies the insurer prices the contract at its expected loss. However, the need to satisfy a survival constraint implies an additional load on the premium, equal to the cost of the additional capital required to ensure the portfolio-wide survival constraint is still met.

Expected losses and capital loads

Assuming a single probability distribution is appropriate to characterise the insurer’s losses on its portfolio, the expected loss $L_{c}$ is precisely estimated, as are the capital reserves, which can be set so that they are just sufficient to cover the loss $(-)x$ at a pre-specified probability $\theta$ (e.g. 1/200 years or 0.005).⁹ For portfolio f the capital reserves are

$$\begin{aligned} Z_{f}=\min \left\{ x:P_{f}(-x)\le \theta \right\} , \end{aligned}$$

(2)

where $P_{f}(x)\equiv P_{f}\left( z:z<x\right)$, i.e. it is shorthand for the probability that portfolio f pays out any amount less than x, or equivalently that the loss is more than x.

The key question is what to do when multiple conflicting estimates of $P_{f}(x)$ are available and there is no basis for assuming one estimate is precisely correct. This might often be the case when insuring catastrophe risks such as hurricanes. The insurer may have at its disposal a set of estimates from the various catastrophe models available.

One approach is to blend the various estimates into a single probability distribution and proceed exactly as above. There are several ways to blend models, but the principal methods are frequency and severity blending.¹⁰ Their workings will be described below.¹¹

Dietz and Walker (2019) propose an alternative approach. Where $\pi$ is an estimate of the probability distribution of losses—call it a ‘model’ for short—the expected loss $L_{c}$ is simply the expectation of the expected losses estimated by each $\pi$.¹² On the other hand, in setting capital reserves the insurer may not be neutral towards the existence of ambiguity and this implies not simply taking expectations. Thus, applying recent developments in economic theory, Dietz and Walker (2019) propose that capital reserves be set according to

$$\begin{aligned} Z_{f}=\min \left\{ x:\alpha \cdot \left[ \underset{\pi \in \varPi }{\mathrm {max}}P_{f}^{\pi }(-x)\right] +(1-\alpha )\cdot \left[ \underset{\pi \in \varPi }{\mathrm {min}}P_{f}^{\pi }(-x)\right] \le \theta \right\} , \end{aligned}$$

(3)

where $\varPi \in {\mathbb {Z}}^{+}$ is the set of all models. The insurer computes $Z_{f}$ by taking a weighted average of the highest and lowest estimates of the loss $(-)x$ at probability $\theta$. The weight factor $\alpha$ captures the insurer’s attitude to ambiguity.¹³ Notice that ambiguity aversion affects the capital reserves, but not the expected loss. This just follows from the assumption that the insurer’s objective is to maximise expected profit subject to a survival constraint.

Dietz and Walker (2019) go on to show that, if one portfolio is more ambiguous than another¹⁴ in a specific sense, then an insurer holds more capital if and only if $\alpha > 0.5$. In other words, an insurer with $\alpha > (<)\,0.5$ is ambiguity-averse (-seeking) and charges higher (lower) premiums for contracts that increase the ambiguity of the portfolio, all else being equal. This comes about because an insurer with $\alpha >0.5$ places more weight on the highest loss estimate, the worst case. In the limit of $\alpha =1$, the insurer sets its capital reserves based exclusively on the worst case, which is analogous to (unweighted) maxmin decision rules that have been proposed as a means of making rational decisions under ambiguity/ignorance (e.g. Gilboa and Schmeidler 1989; Hansen and Sargent 2008). The specific case Dietz and Walker analyse is a set of models $\varPi$ that is centrally symmetric. One portfolio is more ambiguous than another, all else being equal, when it has the same loss distribution at the centre, but where the loss distribution depends more strongly on the true model $\pi$. If $\varPi$ is not centrally symmetric, then it is not true in general that $\alpha >0.5$ corresponds to ambiguity aversion.

Model blending

As mentioned above, instead of Dietz and Walker’s (2019) approach, the insurer could blend the set of models into a single probability distribution and set its capital reserves just using (2). This approach does not allow for ambiguity aversion (seeking). Frequency blending works by taking the weighted average of the probabilities estimated by each of the set of models $\varPi$ of a given loss:

$$\begin{aligned} P_{f}(-x)=\sum _{\pi }\gamma _{\pi }P_{f}^{\pi }(-x), \end{aligned}$$

(4)

where $\gamma _{\pi }$ is the weight assigned to model $\pi$ (see Fig. 1 for a schematic representation). Clearly if each model weight in the set is equal to $1/\varPi$, then (4) is equivalent to computing the arithmetic mean of the probabilities at a given loss, which is a common and natural starting point.

Severity blending involves taking the weighted average of the losses estimated by the models at a given probability:

$$\begin{aligned} P_{f}(-x)=P_{f}\left[ \sum _{\pi }\gamma _{\pi }\text { inv}P_{f}^{\pi }(-x^{\pi })\left| P_{f}^{j}=P_{f}^{k},\forall \pi =j,k\right. \right] . \end{aligned}$$

(5)

See Fig. 1. If each model weight is equal to $1/\varPi$, then (5) is equivalent to computing the arithmetic mean of the losses at a given probability.

Although severity blending might appear to be the inverse of frequency blending, it is not. It is well known that the two techniques tend to produce different estimates of the composite loss distribution, even in relatively trivial examples where there are two models and $\gamma _{1}=\gamma _{2}=0.5$ (see Calder et al. 2012, pp. 18–21). Although severity blending involves applying the inverse of the loss distribution function, $\text {inv}P_{f}^{\pi }(-x)$, the weighted average loss at a given probability need not lead to the same result as the weighted average probability at a given loss. Only in two cases will frequency and severity blending yield exactly the same estimate of $P_{f}(-x)$. One is the trivial case where the models agree exactly on the probability of a given loss, $P_{f}^{j}=P_{f}^{k},\forall \pi =j,k$. The other is when the slopes of the loss distribution functions are equal, that is, for all pairs of models j and k, when $P_{f}^{j\prime }(-x^{j})=P_{f}^{k\prime }(-x^{k})$ over the interval $\left[ -x^{j},-x^{k}\right]$. See Appendix 1.

Fig. 1

Schematic representation of frequency and severity blending of exceedance probability curves

It has been argued that frequency blending is superior to severity blending. While severity blending is easy to perform, doing so breaks the link with the underlying event set, which makes it difficult to make comparisons, such as the accumulation of risk from a given peril across the insurer’s whole portfolio, or the comparison between losses gross and net of excess (Calder et al. 2012; Cook 2011). Nevertheless both techniques are common and so we will evaluate both.

It is possible to envisage a situation in which the application of the $\alpha$-maxmin reserving rule in (3) is mathematically equivalent to using frequency blending to mix models so that reserving rule (2) can be applied (or to using severity blending under the limited circumstances described above). This would be the case if, for example, there were two models and the ambiguity parameter $\alpha$ happened to coincide with the model weights $\left\{ \gamma _{\pi }\right\} _{\pi =1}^{2}$. For instance, the insurer might set $\alpha =0.5$ and consider each of the models to be equally likely to be the true model $(\gamma _{1}=\gamma _{2}=0.5$). However, it is important to stress that $\alpha$ is a behavioural/preference parameter that is intended to capture the insurer’s attitude to ambiguity, whereas the model weights $\gamma _{\pi }$ reflect the insurer’s beliefs about how likely each model is to be the true model. They are conceptually quite different.

Applications to hurricane risk

In this section, we estimate premiums in two case studies, both of which involve catastrophe modelling of hurricane risk and both of which are affected by ambiguity. On the one hand, we estimate premiums based on a single estimate of the probability of losses. This can be obtained either conditional on each model, or by frequency or severity blending. On the other hand, we estimate premiums obtained when the capital holding is set according to the $\alpha$-maxmin rule (3). In both case studies, the problem is simplified to that of a stand-alone, large-contract-cum-small-portfolio ($Z_{f}=0$ in Eq. (1)). Therefore we abstract from issues created by the interaction of the new contract with an insurer’s existing portfolio, as well as from other complications such as deductibles and limits. For these and other reasons that will become apparent, the case studies are not entirely realistic. Limitations to the availability of data constitute a barrier to full realism. Nonetheless our hope is that the case studies are plausible enough to demonstrate the utility of the $\alpha$-maxmin rule relative to model blending.

Florida property

The first case considers ambiguity affecting the insurance of a large portfolio of ca. 5 million residential buildings in Florida against wind damage from hurricanes. The data are taken from Ranger and Niehörster (2012). Ambiguity comes from a set of models of hurricane activity, i.e. the occurrence probabilities of catastrophic hurricane events are imprecisely known. The set of models is generated by taking a set of global climate models and using different models—both dynamical¹⁵ and statistical—to downscale the boundary conditions from the global climate models to Atlantic hurricane activity. Our set comprises 15 models. The estimates of hurricane activity from these 15 models are then used to set the occurrence probabilities of hurricane events (e.g. the event rates) in a single, simplified hurricane risk model (from Risk Management Solutions Inc.), yielding 15 competing exceedance probability (EP) curves.¹⁶ We interpret the loss forecasts provided by Ranger and Niehörster for the year 2020 as the complete set of estimates of present-day losses. This implies all the ambiguity comes from modelling the hazard, whereas in reality ambiguity often stems from uncertain vulnerability functions or exposure characteristics too.

The 15 EP curves are used to calculate average annual losses (AALs, equivalent to $L_{c}$ in Eq. (1)) and losses at specific return periods, and these enable us to estimate premiums if we abstract from the pre-existing portfolio. Figure 2 displays the premium conditional on each hurricane model. It also displays ambiguity-adjusted premiums, with the insurer’s capital reserves set according to the $\alpha$-maxmin rule (3), as well as premiums based on using frequency and severity blending of the models to obtain the AAL and the insurer’s reserves via Eq. (2).¹⁷ Each of the 15 model EP curves is given equal weight when carrying out frequency and severity blending, i.e. $\gamma _{\pi }=1/\varPi ,\forall \pi$. Clearly other model weighting schemes are possible and can be derived by different validation techniques (Mitchell-Wallace et al. 2017), or by credibility theory (Dean 1997). However, equal weighting is consistent with the principle of insufficient reason and the view of Ranger and Niehörster was that there was no straightforward way of establishing relative confidence in each model. In all cases, the insurer is required to hold capital sufficient to cover a 1/200-year event and the cost of capital is assumed to be 10%.

Fig. 2

Premiums for a portfolio of Florida residential property under event rates derived from different hazard models

The range of premiums estimated is from $8.8 billion under the UKMO-HADCM3 model (a global climate model dynamically downscaled) to $16.3bn under the MDR-SST model (a statistical model predicting hurricane formation based on the sea surface temperature in the Atlantic Main Development Region). An insurer with $\alpha =0.5$ requires a premium of $11.3bn. This is an important benchmark: an insurer with $\alpha >(<)\,0.5$ will charge a higher (lower) premium for a contract that is more ambiguous under the specific conditions analysed in Dietz and Walker (2019) and discussed above. The premium of $11.3bn is comprised of an AAL of $3.8bn and a capital load of $7.5bn, thus the premium is three times the expected loss (expectations taken over all 15 models). A maximally ambiguity-averse insurer with $\alpha =1$ sets its premium equal to the expected AAL plus the capital required to absorb the 1/200-year loss in the most pessimistic model, MDR-SST. The resulting premium is $13.6bn, 20% higher than when $\alpha =0.5$, and the price multiple of the expected loss rises to 3.5.¹⁸ Note that this premium is lower than the premium conditional on MDR-SST itself, because the expected AAL over all 15 models is lower than the AAL predicted by MDR-SST.

One of the key results contained in Fig. 2 is that frequency and severity blending produce premiums consistent with Eq. (3) when $\alpha <0.5$. This implies relatively low aversion to ambiguity, possibly ambiguity seeking. The premium is particularly low under frequency blending; it is lower than the premium conditional on 12/15 models. Inspecting the figure, it is clear that the most pessimistic model, MDR-SST, is an outlier and contributes significantly to the premium when $\alpha$ is high. However, note that if MDR-SST is (arbitrarily) removed from the set of models, while the resulting premium under severity blending is now just above the premium corresponding to $\alpha =0.5$, the premium under frequency blending remains below it.¹⁹ Figure 3 shows that the frequency-blended EP curve gives lower losses than the severity-blended EP curve. Applying the theory set out in Appendix 1, this is driven by the slope of the more pessimistic EP curves being initially higher.

Fig. 3

Exceedence probability curves under 15 models of hurricane formation and based on frequency and severity blending (vertical axis is truncated at $120bn for ease of inspection)

In Fig. 4, we repeat the analysis, but instead require insurers to hold sufficient capital to survive a 1/500-year loss. All premiums and multiples are higher, but they are slightly less sensitive to $\alpha$. For $\alpha =1$, the multiple of the price above the expected loss is 4.5. The premium is 16% higher than when $\alpha =0.5$. This reflects the fact that the models are marginally less dispersed in their estimates of the 1/500-year event than they are of the 1/200-year event.²⁰ Frequency and severity blending still give rise to premiums consistent with $\alpha <0.5$. Notice that a minimally ambiguity-averse insurer with $\alpha =0$ charges a premium below that conditional on the most optimistic model, UKMO-HADCM3. This is explained by the fact that, although UKMO-HADCM3 forecasts the lowest AAL, it does not forecast the lowest 1/500-year losses (the model WNDSHR&MDR-SST does²¹).

Fig. 4

Premiums for a portfolio of Florida residential property, where insurers hold capital to cover 1/500-year loss

Dominica property

The second case considers ambiguity affecting the insurance of a portfolio of 3,000 low-income residential properties on the Caribbean island of Dominica against hurricane wind damage. The data come from a study by RMS et al. (2018). In this case there is a single hazard model and ambiguity comes from a set of six vulnerability functions, based on different assumptions about the construction quality of buildings in the portfolio.

As in case 1, the six EP curves are used to calculate AALs, losses at specific, high return periods against which capital reserves are set, and then premiums. Figure 5 displays premiums where capital reserves are set against the 1/200-year event and the cost of capital is 10%. The six models are assigned equal weight for model blending. The range of premiums is from $469,580 under the lowest vulnerability function to about $1.4 million under the highest. An insurer with $\alpha =0.5$ requires a premium of $934,322, which is five times the expected loss of $184,516. This premium is higher than the premiums conditional on 5/6 models, reflecting how much higher losses are under the highest vulnerability function (no protection) than the other five. This also explains why the multiple is as much as five. The difference in premium between $\alpha =0.5$ and $\alpha =1$ is $397,769 or 43%. In this case, we again find that frequency and severity blending give rise to premiums consistent with $\alpha <0.5$.

Fig. 5

Premiums for a portfolio of Dominican residential property under different vulnerability models

The implications of model blending for an insurer’s attitude to ambiguity depend on the model weighting scheme. To demonstrate this, here we implement a purely illustrative scheme, according to which the model using the highest vulnerability function (no protection) is over-weighted at $\gamma _{\text {no}}=0.4$, the three models using vulnerability functions that assume partial roof reinforcement are given a probability of 0.15, and the two models using the lower vulnerability functions (full retrofit) are assigned $\gamma _{\pi }=0.075$. Figure 6 shows that in this case severity blending gives a higher premium than $\alpha =0.5$, but frequency blending still gives rise to a lower premium.

Fig. 6

Premiums for Dominican residential property with an illustrative scheme of unequal model weights

This result suggests a relationship between the weight placed on the model using the highest vulnerability function and the premium required under model blending. Figure 7 traces that relationship, where $\gamma _{\text {no}}$ is the probability assigned to no protection and the weights of the remaining five models are kept equal to $\left( 1-\gamma _{\text {no}}\right) /5$. Figure 7 shows that the no protection model needs to be assigned a weight of $\gamma _{\text {no}}>0.28$ if severity blending is to be consistent with $\alpha >0.5$, while it needs to be assigned a weight of $\gamma _{\text {no}}>0.69$ if frequency blending is to be consistent with $\alpha >0.5$.

Fig. 7

Premiums for Dominican property as a function of weight assigned to highest loss model, no protection

Discussion

The two case studies in this paper have demonstrated the application of a premium principle, which is based on expected profit maximisation, combined with a survival constraint that is based on an $\alpha$-maxmin rule for mixing the least and most pessimistic estimates of the risk of ruin. The analysis has shown that the $\alpha$-maxmin rule lends itself quite naturally to a setting in which there is a finite number of competing catastrophe models.

The main point is to show how the ambiguity load can be linked explicitly to the insurer’s attitude to ambiguity, $\alpha$. This naturally begs the question of what an insurer’s value of $\alpha$ should be and how it might be calibrated. This is not straightforward to answer at this stage. Since the notion of applying the $\alpha$-maxmin rule to insurance pricing is new, no directly relevant empirical evidence on insurers’ $\alpha$ exists.²² Our suggestion is to take a reflexive approach, whereby the insurer considers premiums, multiples and ambiguity loads implied by various values of $\alpha$, and uses the results to determine what the insurer thinks its $\alpha$ should be. There is a certain parallel here with how Ellsberg (1961) and others (e.g. Gilboa et al. 2009) have sought to justify ambiguity aversion as a feature of rational behaviour in the round: namely confront subjects with their behaviour in Ellsberg-type experiments and get them to reflect on whether this behaviour appears rational to them. Insofar as the insurer wishes to set premiums consistent with relatively high ambiguity aversion, $0.5<\alpha \le 1$ is a plausible range within which to narrow down.

The $\alpha$-maxmin model, which is the inspiration behind Dietz and Walker’s (2019) model of insurers’ capital reserving, is just one of several decision rules that have been proposed to represent ambiguity aversion: future work should apply others in the context of insurance pricing. Within a framework of multiple models/priors, one of the chief attractions of $\alpha$-maxmin is that it generalises the earlier maxmin expected utility model of Gilboa and Schmeidler (1989), achieving a separation between decision makers’ taste for ambiguity and their beliefs about the likelihood of different outcomes, and allowing for less pessimistic decision-making than maxmin expected utility, which focuses entirely on the most pessimistic model. However, $\alpha$-maxmin does not admit any information about the relative likelihoods of different models. One simply computes a weighted combination of the least and most pessimistic models. By contrast, a popular model of ambiguity aversion that admits second-order probabilistic beliefs about the models themselves is the ‘smooth ambiguity’ model of Klibanoff et al. (2005). In this model, one not only computes expectations conditional on each model, one also computes a weighted expectation over the set of all models, with the weights reflecting decision makers’ degree of ambiguity aversion. A challenge facing both the $\alpha$-maxmin and smooth ambiguity models is how to define the set of models $\varPi$. Robust control approaches (e.g. Hansen and Sargent 2008) make explicit the process of searching over a space of possible models. They have been applied to insurance problems by Zhu (2011), for instance. There is also an emerging literature in economic theory on unawareness, particularly awareness of unawareness, in which rational decision-makers are modelled as being aware that their perception of the decision problem could in some way be incomplete, i.e. principally that their subjective state space could be incomplete (Walker and Dietz 2011; Lehrer and Teper 2014; Alon 2015; Grant and Quiggin 2015; Karni and Vierø 2017; Kochov 2018). This speaks to the question of whether the insurer’s set of models $\varPi$ is complete. All of these unawareness theories allow for precautionary behaviour (some require it). It may in future be possible to apply some of these frameworks to insurance (e.g. the framework of Alon 2015), although at present they start from the position of an expected utility maximiser, so it is unclear how they can be reconciled with a framework in which there is some degree of well-defined ambiguity to start with. Thus we would argue, perhaps fittingly, that there is no unambiguously preferred model of decision-making under ambiguity/uncertainty.

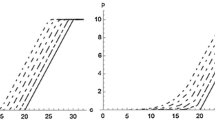
If the insurer suspects that $\varPi$ is incomplete, what are the implications for pricing? One practical implication is that, insofar as the insurer wishes to exercise further caution in the face of awareness of its unawareness, the continued use of an ad hoc premium multiplier could be justified, if the insurer suspects losses could exceed those in the most pessimistic model. In practice, it may be infeasible to include the full set of available catastrophe models when estimating reserves and premiums, due for instance to cost, or a lack of in-house expertise to run them. The question then arising is whether a particular subset of models would suffice. Using data from the Florida property case, Fig. 8 shows the premium estimated by applying the $\alpha$-maxmin rule to the full set of models (left-hand side) and compares this with the premium estimated when one of the 15 hurricane models is omitted (i.e. the premium is estimated over $\varPi -1$ models). This is repeated for each of the 15 models. In addition, on the right-hand side is the premium estimated using just the least and most pessimistic models (with respect to the 1/200-year loss). The figure illustrates two points. First, given the way in which the $\alpha$-maxmin rule takes a convex combination of the least and most pessimistic models to estimate the capital load, the premium is naturally relatively insensitive to removing any model except these two. This suggests it is important for insurers to acquire the least and most pessimistic models, insofar as this is known. Second, just using the least and most pessimistic models does not, however, provide a good approximation of the full set, at least in this case. This is because combining just these two models significantly overestimates the AAL. This in turn stems from the fact that, while WNDSHR&MDR-SST has the lowest 1/200 loss, it actually has quite a high AAL.

Fig. 8

Premiums for a portfolio of Florida residential property under different model subsets

An implication of the analysis is that frequency and severity blending can lead to premiums consistent with relatively low insurer ambiguity aversion. This follows straightforwardly from the observation that the premium estimated by these two blending methods is often lower than that estimated by the $\alpha$-maxmin rule when $\alpha =0.5$. For this result, we need only interpret premium pricing under the $\alpha$-maxmin rule as a representation, rather than a recommendation. Clearly whether there is an inconsistency is context-dependent. All we have sought to do is provide plausible examples.

If the insurer would subsequently apply an ad hoc adjustment to the premium estimated via model blending, the premium could still be consistent with $\alpha >0.5$, of course. We can use the results above to illustrate how large this adjustment would need to be. Taking the leading examples presented in Figs. 2 and 5, the multiplier on the premium estimated via frequency blending would need to be at least 1.15 for the Florida property portfolio and 1.3 for the Dominica property portfolio. If severity blending is used, then the resulting multipliers would need to be at least 1.08 for the Florida property portfolio and 1.09 for the Dominica property portfolio. Nonetheless in our view the use of ad hoc multipliers is better limited to conservatism in the face of unspecified contingencies, as discussed above.

Appendix 1: When do frequency and severity blending give the same result?

In order for frequency and severity blending to yield the same estimate of $P_{f}(-x)$, from Eqs. (4) and (5) it must be that

$$\begin{aligned} \sum _{\pi }\gamma _{\pi }P_{f}^{\pi }(-x)= & {} P_{f}\left[ \sum _{\pi }\gamma _{\pi }\text { inv}P_{f}^{\pi }(-x^{\pi })\left| P_{f}^{j}=P_{f}^{k},\forall \pi =j,k\right. \right] . \end{aligned}$$

Using Jensen’s inequality, a necessary and sufficient condition for this is that $P_{f}^{j\prime }(-x^{j})=P_{f}^{k\prime }(-x^{k})$ for all j, k over the interval $\left[ -x^{j},-x^{k}\right]$, i.e. all model loss distribution functions have the same slope, or in other words the reduction in probability is the same for a given increase in loss. This is trivially the case when $P_{f}^{j}(-x)=P_{f}^{k}(-x)$ for all j, k, i.e. all models agree and there is no ambiguity, but may occasionally be the case in other situations too.

Take any pair of models and suppose the more pessimistic model is j and the more optimistic model is k, in the sense that j estimates a higher probability of a given loss. Then Jensen’s inequality also implies

$$\begin{aligned} \sum _{\pi }\gamma _{\pi }P_{f}^{\pi }(-x)\ge \left( \le \right) P_{f}\left[ \sum _{\pi }\gamma _{\pi }\text { inv}P_{f}^{\pi }(-x^{\pi })\left| P_{f}^{j}=P_{f}^{k},\forall \pi =j,k\right. \right] \end{aligned}$$

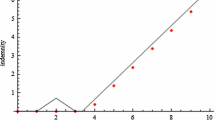
if and only if $P_{f}^{j\prime }(-x^{j})\ge \left( \le \right) P_{f}^{k\prime }(-x^{k})$ for all j, k over the interval $\left[ -x^{j},-x^{k}\right]$. This says—in strong form—that frequency blending yields at least as high an estimate of the probability of loss $-x$ if and only if the slope of the more pessimistic loss distribution function j is higher than its counterpart k, for all j, k, and vice versa. Figure 9 provides a schematic representation. If this is true, then given slope of the more pessimistic function is always higher, we will observe an increasing dispersion of model estimates over the relevant range of losses.

Sometimes, as in Sect. 4, it is more intuitive to perform the inverse mapping of return periods to losses. Then the logic is the inverse too: severity blending yields a higher estimate of the probability of loss $-x$ if and only if the slope of the more pessimistic inverse loss distribution function j is higher than its counterpart k, for all j, k, and vice versa. This intuition is used to explain what we see in Fig. 3.

Fig. 9

Schematic representation of Jensen’s inequality as applied to model blending