Abstract
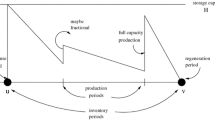
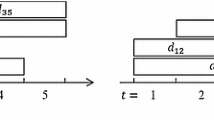
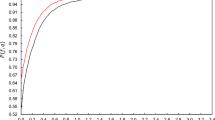
We address the multi-item, capacitated lot-sizing problem (CLSP) encountered in environments where demand is dynamic and to be met on time. Items compete for a limited capacity resource, which requires a setup for each lot of items to be produced causing unproductive time but no direct costs. The problem belongs to a class of problems that are difficult to solve. Even the feasibility problem becomes combinatorial when setup times are considered. This difficulty in reaching optimality and the practical relevance of CLSP make it important to design and analyse heuristics to find good solutions that can be implemented in practice. We consider certain mixed integer programming formulations of the problem and develop heuristics including a curtailed branch and bound, for rounding the setup variables in the LP solution of the tighter formulations. We report our computational results for a class of instances taken from literature.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alfieri A, Brandimarte P and D’Orazio S (2002). LP-based heuristics for the capacitated lot-sizing problem: the interaction of model formulation and solution algorithm. Int J Prod Res 40: 441–458.
Bahl HC and Zionts S (1987). Multi-item scheduling by Benders’ decomposition. J Opl Res Soc 38: 1141–1148.
Barany I, Van Roy TJ and Wolsey LA (1984). Uncapacitated lot sizing: the convex hull of solutions. Math Program Stud 22: 32–43.
Diaby M, Bahl HC, Karwan MH and Zionts S (1992). Capacitated lot-sizing and scheduling by Lagrangean Relaxation. Eur J Opl Res 59: 444–458.
Eppen GD and Martin RK (1987). Solving multi-item capacitated lot-sizing problems using variable redefinition. Opns Res 35: 832–848.
Karayel MN (1984). Dual-based heuristics for capacity constrained production scheduling. PhD thesis, University of California, Berkeley.
Karimi B, Fatemi Ghomi SMT and Wilson JM (2003). The capacitated lot sizing problem: a review of models and algorithms. Omega 31: 365–378.
Maes J, McClain JO and Van Wassenhove LN (1991). Multilevel capacitated lot-sizing complexity and LP-based heuristics. Eur J Opl Res 53: 131–148.
Stadtler H (1996). Mixed integer programming model formulations for dynamic multi-item multi-level capacitated lot-sizing. Eur J Opl Res 94: 561–581.
Süral H (1996). Multi-item lot-sizing with setup times. PhD thesis, Middle East Technical University, Ankara.
Trigeiro WW, Thomas LJ and McClain JO (1989). Capacitated lot-sizing with setup times. Mngt Sci 35 (3): 353–366.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Denizel, M., Süral, H. On alternative mixed integer programming formulations and LP-based heuristics for lot-sizing with setup times. J Oper Res Soc 57, 389–399 (2006). https://doi.org/10.1057/palgrave.jors.2601996
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/palgrave.jors.2601996