Abstract
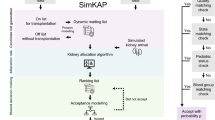
In this article, we present a simulation study on prioritizing patients for receiving scarce cadaveric liver donations. We propose a ranking formula that combines the four criteria commonly used for prioritizing wait-list liver transplant candidates. We apply the proposed ranking formula to evaluate several system outcomes in a liver-allocation simulation model. For each outcome, we identify promising schemes that outperform the currently implemented scheme by analysing the response surfaces constructed with a mixture design of simulation experiments on the four criteria. We also show that it is unlikely to have a scheme that reduces pretransplant mortality and improves other system outcomes simultaneously. Finally, we conduct sensitivity analyses on the two subjective scalars in the ranking formula. Overall, our simulation study shows that the proposed ranking formula and the mixture design approach allow us to systematically analyse patient prioritization in liver transplantation and allocation.




Similar content being viewed by others
References
Alagoz O (2004). Optimal Policies for the Acceptance of Living- and Cadaveric-Donor Livers PhD. Dissertation, University of Pittsburgh, Pittsburgh, PA.
Bjøro K et al (2003). Highly urgent liver transplantation: Possible impact of donor-recipient ABO matching on the outcome after transplantation. Transplantation 75 (3): 347–353.
Box GEP and Wetz J (1973). Criteria for Judging Adequacy of Estimation by an Approximate Response Function. Technical Report. Department of Statistics, University of Wisconsin—Madison.
Cornell JA (1990). Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data. Wiley: New York, NY.
Del Castillo E, Montgomery DC and McCarville DR (1996). Modified desirability functions for multiple response optimization. Journal of Quality Technology 28 (3): 337–345.
Derringer G and Suich R (1980). imultaneous optimization of several response variables. Journal of Quality Technology 12 (4): 214–219.
Draper NR (1984). The Box-Wetz criterion versus R2. Journal of the Royal Statistical Society Series A (General) 147 (1): 100–103.
Feng W-H (2010). Simulation-Based Analysis and Optimization on Recipient Prioritization for Cadaveric Liver Allocation. PhD Dissertation. Purdue University, West Lafayette, IN.
Furukawa H et al (1991). Effect of cold ischemia time on the early outcome of human hepatic allografts preserved with UW solution. Transplantation 51 (5): 1000–1004.
Hastie T, Tibshirani R and Friedman J (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd edn. Springer: New York, NY.
Howard DH (2002). Why do transplant surgeons turn down organs? A model of the accept/reject decision. Journal of Health Economics 21 (6): 957–969.
Institute of Medicine (IoM), Committee on Organ Procurement and Transplantation Policy (1999). Organ Procurement and Transplantation. National Academy Press: Washington, DC.
Kamath PS et al (2001). A model to predict survival in patients with end-stage liver disease. Hepatology 33 (2): 464–470.
Kochanek KD et al (2011). Death: Preliminary Data for 2009. National Vital Statistics Report. 59(4) Centers for Disease Control and Prevention: Atlanta, GA.
Law AM and Kelton WD (2006). Simulation Modeling and Analysis. McGraw Hill: Columbus, OH.
Marcos A et al (1999). Right lobe living donor liver transplantation. Transplantation 68 (6): 798–803.
Myers RH and Montgomery DC (2002). Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 2nd edn. Wiley: New York, NY.
OPTN (2012). The U.S. Organ Procurement and Transplantation Network (OPTN) and the Scientific Registry of Transplant Recipients (SRTR) Annual Report: Transplant Data 2000–2009 Available from http://srtr.trasnplant.hrsa.gov/, accessed January 2012.
Pritsker AAB et al (1995). Organ transplantation policy evaluation. In: Alexopoulos C, Kang K, Lilegdon WR and Goldsman D (eds). Proceedings of the 27th Conference on Winter Simulation. IEEE Computer Society; Washington, DC, pp 1314–1323.
Pritsker AAB, Patrick Daily O and Pritsker KD (1996). Using simulation to craft a national organ transplantation policy. In: Charnes JM, Morrice DJ, Brunner DT and Swain JJ (eds). Proceedings of the 28th Conference on Winter Simulation. IEEE Computer Society; Washington, DC, pp 1163–1169.
Ratcliffe J et al (2001). A simulation modeling approach to evaluating alternative policies for the management of the waiting list for liver transplantation. Health Care Management Science 4 (2): 117–124.
Saaty TL (1999). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. RWS Publications: Pittsburgh, PA.
Saaty TL (2001). Fundamentals for Decision Making and Priority Theory. RWS Publications: Pittsburgh, PA.
Shechter SM et al (2005). A clinically based discrete-event simulation of end-stage liver disease and the organ allocation process. Medical Decision Making 25 (2): 199–209.
Simchi-Levi D, Kaminsky P and Simchi-Levi E (2000). Designing and Managing the Supply Chain: Concepts, Strategies, and Case Studies. McGraw-Hill: Columbus, OH.
Simonoff JS (1998). Smoothing Methods in Statistics. 2nd edn. Springer: New York, NY.
Stahl JE et al (2008). The effect of cold-ischemia time on primary non-function, patient and graft survival in liver transplantation: A system review. PLOS ONE 3 (6): e2468.
Thompson D et al (2004). Simulating the allocation of organs for transplantation. Health Care Management Science 7 (4): 331–338.
Totsuka E et al (2002). Influence of cold ischemia time and graft transport distance on postoperative outcome in human liver transplantation. Surgery Today 32 (9): 792–799.
UNOS (2012). United network for organ sharing data collection: UNetsm. Available from http://optn.transplant.hrsa.gov/data/, accessed January 2012.
Wiesner RH et al (2001). MELD and PELD: Application of survival models to liver allocation. Liver Transplantation 7 (7): 567–580.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
ANOVA tables for system outcomes
For each design point, the number of simulation replications is 10 except for additional footnote under the table.
Rights and permissions
About this article
Cite this article
Feng, WH., Kong, N. & Wan, H. A simulation study of cadaveric liver allocation with a single-score patient prioritization formula. J Simulation 7, 109–125 (2013). https://doi.org/10.1057/jos.2012.21
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/jos.2012.21