Abstract
We solve a one-period asset allocation problem with a Bayesian copula-Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model. Investors invest among risk-free assets, a passive fund and an active fund, and maximize their expected utility. Posterior distributions of model parameters are drawn by the ‘Metropolis-within-Gibbs’ algorithm. Our results show significant percentage of holdings in active funds with different levels of risk aversion. With low risk aversion, Bayesian models yield similar portfolio weights and returns with non-Bayesian models. As risk aversion increases, however, Bayesian models imply more conservative weights in active funds and lead to significantly lower volatility of realized out-of-sample returns and utilities.



Similar content being viewed by others
Notes
See Patton (2004, 2006a, 2006b), Hu (2006), Jondeau and Rockinger (2002) and Tasfack (2006).
Random-walk H-M algorithm generates highly correlated data points and we usually need to extract each data point from a relatively large number of simulated points. For example, in our case, we extract each data point for every 20 simulated data points.
See Nelson (1998) and Joe (1997) for a formal treatment of copula theory, and Bouye et al (2000), Cherubini et al (2004) and Embrechts et al (2002) for applications of copula theory in finance.
See Patton (2004).
For a detailed survey on the estimations of copula-GARCH model, see Chapter 5 of Cherubini et al (2004).
See Mueller (1991, 1993), Casella and George (1992) and Chib and Greenberg (1995) for a general overview on Gibbs sampling, Metropolis-Hastings sampling and ‘Metropolis-within-Gibbs’ algorithm.
We will not explore this aspect in this article.
The two websites are http://finance.yahoo.com and http://reseaerch.stlouisfed.org/fred2, respectively.
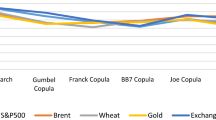
We omit the figures for the other two asset groups to save some space, and they have very similar patterns. Meanwhile, Table 7 covers the statistical patterns of the optimal portfolios for all three asset groups.
References
Ang, A. and Chen, J. (2002) Asymmetric correlations of equity portfolios. Journal of Financial Economics 63: 443–494.
Arnott, R., Berkin, A. and Ye, J. (2000) How well have investors been served in the 1980s and 1990s? The Journal of Portfolio Management 26 4: 84–91.
Baks, K., Metrick, A. and Wachter, J. (2001) Should investors avoid all actively managed mutual funds? A study in Bayesian performance evaluation. The Journal of Finance 56 : 45–85.
Bouye, E., Drrleman, V., Nikeghbali, A., Riboulet, G. and Roncalli, T. (2000) Copulas for Finance: A Reading Guide and Some Applications. Paris, France: Groupe de Recherche Operationelle Credit Lyonnais.
Casella, G. and George, E.I. (1992) Explaining the Gibbs sampler. The American Statistician 46 (3): 167–174.
Cherubini, U., Luciano, E. and Vecchiato, W. (2004) Copula Methods in Finance, Wiley Series in Financial Engineering. Chichester, UK: Wiley.
Chib, S. and Greenberg, E. (1995) Understanding the Metropolis-Hastings algorithm. The American Statistician 49 (4): 327–335.
Elton, E.J., Gruber, M.J. and Blake, C.R. (1996) The persistence of risk-adjusted mutual fund performance. Journal of Business 69 (2): 133–157.
Embrechts, P.M.E., McNeil, A.J. and Straumann, D. (2002) Correlation and dependency in risk management: Properties and pitfalls. In: M. Dempster (ed.) Risk Management: Value at Risk and Beyond. UK: Cambridge University Press, pp. 176–223.
Fortin, R. and Michelson, S. (2002) Indexing versus active mutual fund management. FPA Journal (September), Article 7.
Geweke, J. (1992) Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. Proceedings of the Fourth Valencia International Meeting on Bayesian Statistics, Oxford University Press. pp. 169–194.
Hansen, B.E. (1994) Autoregressive conditional density estimation. International Economic Review 35: 705–730.
Hu, L. (2006) Dependence patterns across financial markets: A mixed copula approach. Applied Financial Economics 16: 717–729.
Joe, H. (1997) Multivariate Models and Dependence Concepts. London: Chapman & Hall.
Joe, H. and Xu, J.J. (1996) The Estimation Method of Inference Functions for Margins for Multivariate Models. Department of Statistics, University of British Columbia, Tech. Rept. 166.
Jondeau, E. and Rockinger, M. (2002) Conditional Dependency of Financial Series: The Copula-GARCH Model. FAME. Working paper.
Jondeau, E. and Rockinger, M. (2003) Conditional volatility, skewness, and kurtosis: Existence, persistence and comovements. Journal of Economic Dynamics and Control 27 (10): 1699–1737.
Longin, F. and Solnik, B. (2001) Extreme correlations in international equity markets. Journal of Finance 56: 649–676.
Malkiel, B. (1995) Returns from investing in equity mutual funds 1971 to 1991. The Journal of Finance 50 (2): 549–572.
Mueller, P. (1991) A General Approach to Posterior Integration and Gibbs Sampling. Purdue University. Technical Report, 91–09.
Mueller, P. (1993) Alternatives to the Gibbs Sampling Scheme. Institute of Statistics and Decision Science, Duke University. Technical Report.
Nelson, R.B. (1998) An Introduction to Copula. New York: Springer-Verlag.
Patton, A.J. (2004) On the out-of-sample importance of skewness and asymmetric dependence for asset allocation. Journal of Financial Econometrics 2 (1): 130–168.
Patton, A.J. (2006a) Modelling asymmetric exchange rate dependence. International Economic Review 47 (2): 527–556.
Patton, A.J. (2006b) Estimation of copula models for time series of possibly different lengths. Journal of Applied Econometrics 21 (2): 147–173.
Raftery, A.E. and Lewis, S.M. (1992a) One long run with diagnostics: Implementation strategies for Markov chain Monte Carlo. Statistical Science 7 : 493–497.
Raftery, A.E. and Lewis, S.M. (1992b) How many iterations in the Gibbs sampler? In: J.M. Bernardo, J.O. Berger, A.P. David and A.F.M. Smith (eds.) Bayesian Statistics 4. Oxford: Oxford University Press, pp. 763–773.
Raftery, A.E. and Lewis, S.M. (1995) The number of iterations, convergence diagnostics and generic Metropolis algorithms. In: W.R. Gilks, D.J. Spiegelhalter and S. Richardson (eds.) Practical Markov Chain Monte Carlo. London, UK: Chapman and Hall.
Sklar, A. (1959) Fonctions de Repartition an Dimensions et Leurs Marges. Publications de l’Institut de Statistique de L’Universite de Paris 8, 229–231.
Smith, A.F.M. and Roberts, G.O. (1993) Bayesian computation via the Gibbs sampler and related Markov Chain Monte Carlo methods. Journal of the Royal Statistical Society, Ser. B, 55: 3–24.
Tasfack, G. (2006) Dependence Structure and Extreme Comovements in International Equity and Bond Markets. Universite de Montreal, CIRANO and CIREQ. Working paper.
Tierney, L. (1994) Markov chains for exploring posterior distributions (with discussion). Annals of Statistics 22: 1701–1762.
Xu, Y. (2004) Incorporating Estimation Risk in Copula-based Portfolio Optimization. Department of Economics, University of Miami. Working paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kang, L. Asset allocation in a Bayesian copula-GARCH framework: An application to the ‘passive funds versus active funds’ problem. J Asset Manag 12, 45–66 (2011). https://doi.org/10.1057/jam.2010.6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/jam.2010.6