Skewness Preference, Risk Taking and Expected Utility Maximisation

Abstract

Available empirical evidence suggests that skewness preference plays an important role in understanding asset pricing and gambling. This paper establishes a skewness-comparability condition on probability distributions that is necessary and sufficient for any decision-maker's preferences over the distributions to depend on their means, variances, and third moments only. Under the condition, an Expected Utility maximizer's preferences for a larger mean, a smaller variance, and a larger third moment are shown to parallel, respectively, his preferences for a first-degree stochastic dominant improvement, a mean-preserving contraction, and a downside risk decrease and are characterized in terms of the von Neumann-Morgenstern utility function in exactly the same way. By showing that all Bernoulli distributions are mutually skewness comparable, we further show that in the wide range of economic models where these distributions are used individuals’ decisions under risk can be understood as trade-offs between mean, variance, and skewness. Our results on skewness-inducing transformations of random variables can also be applied to analyze the effects of progressive tax reforms on the incentive to make risky investments.

Introduction

Do individual decision-makers, other things being equal, prefer a more positively skewed distribution? There is a substantial and growing body of empirical evidence suggesting that they do. Building on the earlier seminal contributions of Arditti (1967) and Kraus and Litzenberger (1976), Harvey and Siddique (2000),¹ for example, show in an asset pricing model that systematic skewness is economically important and commands a substantial premium. Studying the data from horse race betting and from state lotteries (in the U.S.), respectively, Golec and Tamarkin (1998) and Garrett and Sobel (1999) find evidence supporting the contention that gamblers are not necessarily risk lovers but skewness lovers.

So far, however, skewness preference has no firm choice theoretic foundation. Skewness has been treated as synonymous with the (unstandardized) third central moment but it is well-known that preference for a larger third moment is in general not consistent with Expected Utility (EU) maximisation unless the utility function is cubic. As a result, in studies of skewness preference to date, either a cubic utility function is assumed² or a cubic Taylor approximation of the EU is taken (i.e., the utility function is approximated by a Taylor series truncated to three terms before taking expectations). The limitations of these approaches are obvious. A truncated Taylor series, for instance, can be a reasonable approximation only for small risks.³ Menezes et al. (1980) come closest to establish a formal linkage between skewness preference and EU maximisation by showing that a distribution having more “downside risk” implies, but is not implied by, its (unstandardized) third moment being smaller, and that downside risk aversion is characterized by a von Neumann-Morgenstern (VNM) utility function with a positive third derivative.

In the statistics literature, Van Zwet (1964) defines a distribution F to be more positively skewed than G if R(x)≡F⁻¹(G(x)) is convex and it has become widely accepted that a good skewness measure should preserve the skewness ordering so defined (see, for example, Oja (1981) and Arnold and Groeneveld (1995)). Oja (1981) proposes a condition in terms of the number of crossings of two standardized distribution functions that relaxes Van Zwet's (1964) skewness-comparability condition. The preferences of EU maximizing decision-makers over skewness-comparable distributions as defined by these authors, on the other hand, have not been explored and characterized.

This paper establishes a skewness-comparability condition on probability distributions that is necessary and sufficient for any decision-maker's preferences over the distributions to depend on their means, variances, and third moments only. Under the condition, a EU maximizer's preferences for a larger mean, smaller variance, and a larger third moment are shown to parallel, respectively, his preferences for a first-degree stochastic dominant (FSD) improvement, a mean-preserving contraction (MPC), and a downside risk decrease and are characterized in terms of the VNM utility function in exactly the same way. The condition generalizes not just the skewness-comparability conditions proposed by Van Zwet (1964) and Oja (1981) but also the condition for two distributions to be comparable in terms of downside risk defined by Menezes et al. (1980). Furthermore, distributions satisfying the “location-scale” or “linear class” condition of Meyer (1987) and Sinn (1983), which they show to be sufficient for the consistency between the mean-variance analysis and EU maximisation, are shown to be skewness-comparable distributions with identical standardized third moments. By showing that all Bernoulli distributions are mutually skewness comparable, we further show that in the wide range of economic models where these distributions are used individuals’ decisions under risk can be understood as trade-offs between mean, variance, and skewness. Our basic characterizations also immediately imply that a concave transformation of a random variable reduces the skewness of the distribution and hence, other things being equal, the attractiveness of the distribution to a skewness-preferring decision-maker. An application of this general regularity addresses the issue of whether a progressive tax reform reduces the incentive to take risks.

The rest of the paper is organized as follows. Skewness comparability and expected utility maximisation section sets out the basic definitions and main results on skewness comparability. Skewness of the Bernoulli distributions section establishes the skewness comparability of the widely used Bernoulli distributions and examines its implications. Comparison with the existing approach and implications for gambling and tax reforms section concludes with discussions on the comparison with the existing approach to modelling skewness preference, the implications for the decision to gamble, and the effects of progressive tax reforms on risk taking.

Skewness comparability and EU maximisation

Preliminaries and stochastic dominance

Throughout the paper, (cumulative) distribution functions, denoted by F(x),G(x), etc., have the supports of their densities contained in [a, b]. We denote the mean, the variance, and the standardized and the unstandardized third central moments of a distribution F(x) by μ _F , σ _F ², m _F ³, and m̂ _F ³, respectively. That is,

For reasons that will become clear, when the abbreviated term “the third moment” is used in what follows, it refers exclusively to the standardized third central moment, never the unstandardized one. VNM utility functions are denoted by u,v, etc.

For a distribution function F(x), define F⁽¹⁾(x)=F(x) and

The standard notion of nth-degree stochastic dominance is defined as follows:

Definition 1

• The change from F(x) to G(x) is an nth-degree stochastic dominant improvement (deterioration) if [G⁽ⁿ⁾(x)−F⁽ⁿ⁾(x)]⩽(⩾)0 for all x∈[a, b], where the inequality is strict for some subinterval (s), and [G^(k)(b)−F^(k)(b)]⩽(⩾)0 for k=2, … n−1.

We will henceforth use [F(x) → G(x)] as a shorthand for the change of distributions from F(x) to G(x). It is well-known that ∫ _a ^bu(y)d[G(y)−F(y)]>0 for all u(x) such that u′(x)>0 for all x if and only if [F(x) → G(x)] is a FSD improvement. The related notions of a mean-preserving spread (contraction) and a downside risk increase (decrease) can be defined as special cases of stochastic dominant deterioration (improvement).

Definition 2

• (i) A second-degree stochastic dominant deterioration (improvement) is a mean-preserving spread (contraction) [MPS (MPC)] if [G⁽²⁾(b)−F⁽²⁾(b)]=0.

(ii) A third-degree stochastic dominant deterioration (improvement) is a downside risk increase (decrease) if [G⁽²⁾(b)−F⁽²⁾(b)]=0 and [G⁽³⁾(b)−F⁽³⁾(b)]=0.

The definitions of an MPS and a downside risk increase here are, of course, equivalent to those in Rothschild and Stiglitz (1970) and Menezes et al. (1980), respectively. Menezes et al. (1980) show that ∫ _a ^bu(y)d[G(y)−F(y)]<0 for all u(x) such that u′′′(x)>0 for all x if and only if [F(x) → G(x)] is a downside risk increase. They further show the following:

Lemma 1

• (Menezes et al.) [G(x) → F(x)] being a downside risk increase implies, but is not implied by, m _F ³<m _G ³.

The better known result of Rothschild and Stiglitz (1970) on the other hand establishes that ∫ _a ^bu(y)d[G(y)−F(y)]<0 for all u(x) such that u′′(x)<0 for all x if and only if [F(x) → G(x)] is an MPS.

Skewness comparability

Van Zwet (1964, p. 9) argues that since intuitively “convex transformation of a random variable effects a contraction of the lower part of the scale of measurement and an extension of the upper part”, a distribution F can be defined to be more skewed to the right than G if R(x)≡F⁻¹(G(x)) is convex.⁴ It has since become widely accepted that a good skewness measure should preserve the skewness ordering so defined (see, for example, Oja (1981) and Arnold and Groeneveld (1995)). Following Oja (1981), we define strong skewness comparability as follows:

Definition 3

• (i) Distributions F and G are strongly skewness comparable if F⁻¹(G(x)) is convex or concave.

  (ii) F is more skewed to the right than G in the sense of Van Zwet if F⁻¹(G(x)) is convex.

The condition for skewness comparability is however too strong and may not be strictly satisfied in many typical cases where one distribution is considered more skewed than another such as distributions F and G and their respective density functions f and g illustrated in Figures 1 and 2. We observe in Figures 1 and 2 that if two distributions have the same mean and, loosely speaking, the same “spread” as depicted, then one distribution being more skewed to the right typically implies the two distribution functions cross twice. However, in cases such as depicted, F⁻¹ may or may not be an exact convex transformation of G⁻¹ as is required by Van Zwet's definition. Noting that if F(x) is the distribution function for a random variable x̃, then F(σ _F x+μ _F ) is the distribution for the standardized random variable (x̃−μ _F )/σ _F , we state Oja's (1981) weaker comparability condition as follows:

Definition 4

• (i) Distribution s F and G are skewness comparable in the sense of Oja if G(σ _G x+μ _G ) crosses F(σ _F x+μ _F ) exactly twice or F(σ _F x+μ _F )=G(σ _G x+μ _G ).

  (ii) F is more skewed to the right than G in the sense of Oja if G(σ _G x+μG) crosses F(σ _F x+μ _F ) exactly twice first from above.

Figure 1

The density functions f and g.

Figure 2

F(x) and G(x).

The following lemma confirms that this is a weaker notion of skewness comparability and relates it to the concept of increasing downside risk of Menezes et al. (1980).⁵

Lemma 2

• (i) If F and G are strongly skewness comparable, then they are skewness comparable in the sense of Oja.

  (ii) If F is more skewed to the right than G in the sense of Oja, then [F(σ _F x+μ _F ) → G(σ _G x+μ _G )] is a downside risk increase.

In view of Lemma 2, we define our notion of “generalized skewness comparability” based on the notion of a downside risk increase and show that this is a necessary and sufficient condition for preferences over two distributions to be determined by their means, variances, and third moments alone. For expositional ease, we henceforth simply use “skewness comparability” to mean “generalized skewness comparability”.

Definition 5

• (i) Distributions F and G are (generalized) skewness comparable if [F(σ _F x+μ _F ) → G(σ _G x+μ _G )] is a downside risk increase or a downside risk decrease or F(σ _F x+μ _F )=G(σ _G x+μ _G ).

  (ii) F is more skewed to the right than G if [F(σ _F x+μ _F ) → G(σ _G x+μ _G )] is a downside risk increase.⁶

Theorem 1

• μ _F =μ _G , σ _F ²=σ _G ², and m _F ³=m _G ³ imply F(x)=G(x) if and only if F and G are skewness comparable.

The result clearly shows that any decision-maker's preferences over skewness-comparable distributions are determined by the first three moments of the distributions. We, however, restrict our attention to EU theory because it remains the only widely used decision model known to be consistent with downside risk aversion.⁷ The result implies, in particular, that for skewness-comparable changes in a distribution F, U(μ _F ,σ _F ²,m _F ³)≡∫ _a ^bu(x)dF(x) is a well-defined function from R × R⁺ × R to R. We next show that for skewness-comparable distributions, an EU maximizer's preferences for a larger mean, a smaller variance, and a larger third moment parallel, respectively, his preferences for a FSD improvement, an MPC, and a downside risk decrease and are characterized in terms of the VNM utility function in exactly the same way.

Theorem 2

• (i) Supposing μ _F =μ _G and σ _F ²=σ _G ², then m _F ³>m _G ³ implies ∫ _a ^bu(x)dF(x)>∫ _a ^bu(x)dG(x) for any two skewness-comparable distributions F and G if and only if u′′′(x)>0 for all x.

  (ii) Supposing μ _F =μ _G and m _F ³=m _G ³, then σ _F ²>σ _G ² implies ∫ _a ^bu(x)dF(x)<∫ _a ^bu(x)dG(x) for any two skewness-comparable distributions F and G if and only if u′′(x)<0 for all x.

  (iii) Supposing σ _F ²=σ _G ² and m _F ³=m _G ³, then μ _F >μ _G implies ∫ _a ^bu(x)dF(x)>∫ _a ^bu(x)dG(x) for any two skewness-comparable distributions F and G if and only if u′(x)>0 for all x.

Or equivalently,

Theorem 2a

• U(μ _F ,σ _F ²,m _F ³)=∫ _a ^bu(x)dF(x) is increasing in μ _F and m _F ³ and decreasing in σ _F ² for skewness-comparable changes in any distribution F if and only if u′(x)>0, u′′(x)<0, and u′′′(x)>0 for all x.

With standard results in Rothschild and Stiglitz (1970) and Menezes et al. (1980), the result is implied by the following lemma, which may be of independent interest.

Lemma 3

• Suppose F and G are (generalized) skewness comparable. Then

  (i) m _F ³>m _G ³ if and only if F is more skewed to the right than G.

  (ii) Assuming μ _F =μ _G and m _F ³=m _G ³, σ _F ²>σ _G ² if and only if [G(x) → F(x)] is an MPS.

  (iii) Assuming σ _F ²=σ _G ² and m _F ³=m _G ³, μ _F >μ _G if and only if [G(x) → F(x)] is an FSD improvement.

For any two skewness-comparable distributions F and G, we can thus have a simple and useful decomposition of the difference in EU as follows.

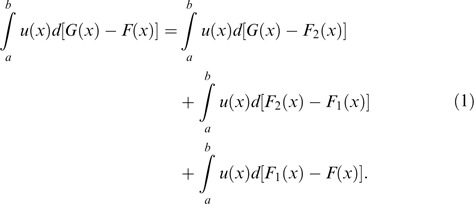
where F₁(x)≡F(x+μ _F −μ _G ) and . Hence F₁ and F differ only by their means, F₂ and F₁ have the same mean and , and [F₂(x) → G(x)] is a downside risk increase or decrease or G(x)=F₂(x). As will be shown, such a simple decomposition, which depicts trade-offs between mean, variance (or risk), and skewness, is useful in understanding individuals’ choice among skewness-comparable distributions.

Sinn (1983) and Meyer (1987) define that two distributions F and G are in the “linear class” or the “location-scale” model if F(x)=G(βx+α) with β>0 and show that EU maximizers’ preferences over distributions in this model are determined by the means and variances of the distributions only, that is, mean-variance decision models are consistent with EU maximisation. Meyer (1987) further shows that in many important economic models, including Sandmo's (1971) model of competitive firms facing random output price and Tobin's (1958) theory of liquidity preference with a single risky and riskless asset, comparative statics analysis can be reformulated as choice among distributions in this class. Clearly, if F and G are in the “location-scale” model, F(σ _F x+μ _F )=G(σ _G x+μ _G ). That is, distributions in the “location-scale” model are skewness comparable ones with identical third moments.

Skewness of the Bernoulli distributions

Skewness comparability of the Bernoulli distributions

Their simple parametric structure notwithstanding, the Bernoulli distributions are applicable to a wide range of economic problems and are used in a wide range of economic models. We show that the answer to the question of skewness comparability for this simple but important family of distributions is very clear-cut. Let [(y, p)(z, 1−p)] denote a Bernoulli distribution that gives y with probability p and z with probability (1−p).

Proposition 1

• For i=1,  2, let F _i (x), μ _i and σ _i be the cumulative distribution function, the mean and the standard deviation of [(y _i , p _i )(z _i ,1−p _i )], respectively, and y _i <z _i . Then

  (i) p₁<p₂ if and only if F₂(x) is more skewed to the right than F₁(x).

  (ii) p₁=p₂ if and only if F₁(σ₁x+μ₁)=F₂(σ₂x+μ₂).

The result clearly shows that not only are all Bernoulli distributions skewness comparable but also their degrees of skewness are determined by the parameter p alone.⁸ This gives a novel perspective on individuals’ decisions in the wide range of economic models where the choices available are assumed to be Bernoulli distributions: These decisions can be understood as trade-offs between mean, variance, and skewness. We will illustrate in what follows the usefulness of this perspective in understanding individuals’ betting behaviour and self-protection decisions. The same approach can potentially yield interesting insights in such important models as those of auctions, tournaments, among others. Moreover, the result also shows that if two Bernoulli distributions share the same value for the parameter p, they are not just skewness comparable but also in the “location-scale model” or “linear class” and hence are consistent with mean-variance preferences.

Empirical evidence for Gamblers’ skewness preference

The result that any pair of Bernoulli distributions are skewness comparable indicates that the empirical findings of Golec and Tamarkin (1998) and Garrett and Sobel (1999) do represent evidence for gamblers’ skewness preference as is defined and characterized in this paper. Specifically, a bet on horse h considered by Golec and Tamarkin (1998) (and Ali (1977)) takes the form [(0, 1−p _h )(X _h ,p _h )], where X _h denotes the return of a winning bet on horse h and a losing bet returns zero to the bettor, and assuming bettors have identical utility function u( ), their EU betting on horse h is

Assuming that u(0)=0 and u(X _H )=1, where H represents the highest-odds horse, and that the amount bet on each horse is such that bettors are indifferent between bets on any horse h, for any h, we have

which gives p _H /p _h =u(X _h ). Racetrack data are then used to estimate the utility function assumed to take the cubic form u(X _h )=a+b₁X _h +b₂X _h ²+b₃X _h ³. The estimated coefficients b₁ and b₃ are positive and b₂ negative, all of which are highly significant. The estimated utility function is thus concave for low values of X _h and convex for high values. Bettors are therefore not globally risk loving as suggested by earlier studies such as Ali (1977). More importantly, a utility function with u′′′( )>0 estimated using a data set of skewness-comparable distributions with different degrees of skewness does indicate (global) skewness preference as defined in this paper.⁹ Using data from U.S. state lotteries, Garrett and Sobel (1999) follow the exact same methodology by assuming that lottery players completely disregard the prizes of a lottery other than the top prize (i.e., winning anything other than the top prize of a lottery gives zero utility) and hence a choice among state lotteries is effectively a choice among Bernoulli distributions. They obtain identical results in terms of the characteristics of the utility function. That is, to the extent that lottery players do play only to win the top prize, the state lottery data also support global skewness preference.

Self-protection

Ehrlich and Becker (1972) define self-protection to be the expenditure on reducing the probability of suffering a loss and highlight its conceptual distinction from self-insurance, which is the expenditure on reducing the severity of loss.¹⁰ Denoting the initial wealth by w and the probability of suffering a loss l by p, self-protection is the expenditure on reducing the probability p of the Bernoulli distribution [(w−l, p)(w, 1−p)]. Proposition 1 shows that a reduction in p implies a reduction in (positive) skewness and an EU maximizer's preferences regarding self-protection are completely determined by its effects on the mean, variance, and third moment. Let F and G denote, respectively, the distributions before and after a reduction in p by ɛ, we can explicitly decompose the effect of self-protection as in (1):

where F₁(x)≡F(x+μ _F −μ _G ) and . This gives a novel and definitive characterization of all the relevant factors determining the choice of self-protection and brings together, and offers straightforward interpretations to, results from recent attempts to relate self-protection to skewness preference (i.e., the third derivative of a VNM utility function).¹¹ For example, if the individual pays the fair price ɛl for the reduction in p, then clearly ∫ _a ^bu(x)d[F₁(x)−F(x)]=0. It follows that he is willing to pay more than the fair price for the reduction in loss probability if ∫ _a ^bu(x)d[G(x)−F₂(x)]+∫ _a ^bu(x)d[F₂(x)−F₁(x)]>0. More specifically, the change in variance caused by a reduction in p by ɛ is

If p>1/2, a risk-averse skewness-preferring individual will not be willing to pay the fair price for a small reduction in p, that is, for ɛ⩽(2p−1). On the other hand, if p⩽1/2, self-protection reduces both the skewness and variance and consequently ∫ _a ^bu(x)d[G(x)−F₂(x)]<0 and ∫ _a ^bu(x)d[F₂(x)−F₁(x)]>0. Whether a risk-averse skewness-preferring individual is willing to pay more than the fair price for self-protection depends on the strength of his skewness preference relative to his risk aversion, which, as is shown in Chiu (2005a), the prudence measure, −u′′′(x)/u′′(x), can be interpreted as measuring.¹² The simple decomposition in (1) thus not only offers much more straightforward interpretations for the results in Chiu (2000, 2005b) and Eeckhoudt and Gollier (2005), but also suggests that the problem of self-protection can be analyzed without using the first-order approach, which entails assuming the second-order condition and its implied restrictions on the relationship between the self-protection expenditure and the reduction in the loss probability.¹³

Comparison with the existing approach and implications for gambling and tax reforms

The existing approach to skewness preference

The theoretical justification for considering skewness preference has so far been a Taylor series approximation of the EU. Specifically, letting F be the distribution function for random variable x̃,

Clearly if we have a cubic utility function u(x)=c₀+c₁x+c₂x²+c₃x³, the cubic expansion will be precise and the EU given F can be explicitly calculated as

That is, if either the Taylor series represents a good approximation or the utility is cubic, u′′′(x)>0 appears to imply a preference for the unstandardized third central moment m̂ _F ³.¹⁴ On the one hand, our results in the previous section can be seen as confirming that the EU given a distribution can be written as a function of its mean, variance, and unstandardized third moment for mutually skewness-comparable distributions: since we have shown that a function U(μ _F ,σ _F ²,m _F ³)=∫ _a ^bu(x)dF(x) is well defined for skewness-comparable changes in F, for such changes we can define

On the other hand, what (3), (4), and (5) all say is that, assuming u′′′(x)>0, a larger m̂ _F ³ implies a larger Eu(x̃) if μ _F and σ _F ² are held constant. For two distributions F and G with σ _F ²>σ _G ², in particular, m̂ _F ³>m̂ _G ³ does not imply either that F is more skewed than G or that skewness plays any role in determining their comparative desirability to an individual. This seems to be an insight well-hidden in using the traditional approach, as is exemplified by Tsiang's (1972, p. 363) attempt to explain the Borch (1969) paradox by invoking skewness preference.¹⁵ Other pitfalls in using the traditional approach can also be seen in Markowitz's (1952a) conjecture on skewness preference and the decision to gamble discussed in what follows.

Skewness preference and the decision to gamble

Skewness preference has been associated with gambling since long before the work of Golec and Tamarkin (1998) and Garrett and Sobel (1999). Markowitz (1952a) suggests that “the third moment of the probability distribution of returns from the portfolio may be connected with a propensity to gamble” and that if individuals’ utility of a probability distribution is a function of the third moment as well as the mean and variance of the distribution, then some fair bets would be accepted.¹⁶ So is it possible for an individual with a third-moment utility function who is averse to larger variances, as is usually assumed in the context of mean-variance analysis, to accept an independent fair gamble given a sufficiently strong skewness preference? The Taylor approximation in (3) gives the impression that this is possible. To examine the possibility, suppose an individual with initial wealth distribution F is contemplating taking fair gambles that increase the skewness of F in the sense defined in this paper and are independent of F. Then

is well defined. Consider first the case where U(μ _F ,σ _F ²,m _F ³) is decreasing in σ _F ² and increasing in m _F ³ for all distribution F. Theorem 2a clearly indicates that U(μ _F ,σ _F ²,m _F ³) being decreasing in σ _F ² for all distribution F is equivalent to risk aversion (i.e., u′′(x)<0 for all x) and since accepting a fair gamble independent of his initial wealth induces a MPS, by the classic result of Rothschild and Stiglitz (1970), it always reduces his EU given his risk aversion whatever the strength of his skewness preference. Alternatively, assume that for all distribution F, Û(μ _F ,σ _F ²,m̂ _F ³) is decreasing in σ _F ² and increasing in m _F ³, that is, (assuming differentiability) Û₂(μ _F ,σ _F ²,m̂ _F ³)<0 and Û₃(μ _F ,σ _F ²,m̂ _F ³)>0. Then since U(μ _F ,σ _F ²,m _F ³)=Û(μ _F ,σ _F ²,σ _F ³m _F ³), simple differentiation shows that

Clearly, Û₂(μ _F ,σ _F ²,m _F ³)<0 for all distribution F implies U₂(μ _F ,σ _F ²,m _F ³)<0 for all distribution F because if U₂(μ _F ,σ _F ²,m _F ³)⩾0 for a negatively skewed or symmetrical distribution F, that is, m _F ³⩽0, then (given ₃(μ _F ,σ _F ²,m̂ _F ³)>0) Û₂(μ _F ,σ _F ²,m _F ³)⩾0. In other words, with a third-moment utility function, whether the utility is defined on the standardized or unstandardized third moment, aversion to larger variances implies risk aversion and precludes taking fair gambles whatever the strength of the skewness preference.

The incentive effects of tax reforms

In considering the implications of his pioneering analysis of skewness preference, Tsiang (1972, p. 370) suggests that

the effect of income tax on risk-taking should be examined not only with respect to its impacts on the mean and variance of investment returns after tax, but also with respect to its impacts on the skewness of net returns. A progressive income tax ... could certainly have a greater adverse effect on the willingness to take risk than a proportional tax with perfect loss offset that leave the mean and variance after tax at the same levels.

Does a progressive tax necessarily reduce the skewness of the net returns of a risky investment and hence have a greater adverse effect on the willingness to take risk than a proportional income tax? More generally, since the 1980s, there has been a broad international trend towards the flattening of personal income tax structures. Does such a reform increase the skewness of the after-tax income distribution and as a result, other things being equal, enhance the incentive to make risky investments? Our basic results on skewness preference can be applied to give definitive answers to these questions, under a particular definition of a “more progressive tax” as follows.¹⁷

Definition 6

• A tax schedule t₁(x) is more residual-concave than another t₂(x) if r₁(r₂⁻¹(τ)) is concave where for i=1, 2, r _i (x)≡x−t _i (x) is the residual income function under tax schedule t _i (x).

That is, a tax schedule t₁(x) is more progressive than another t₂(x) in the sense of residual concavity if the residual income function [x−t₁(x)] is a concave transformation of [x−t₂(x)]. Under this definition, any graduated-rate tax is more residual-concave than any proportional tax and a tax schedule becoming less residual-concave more generally defines a particular kind of flattening of the tax schedule. For example, flattening a graduated-rate tax by reducing the top marginal tax rate or by abolishing the income band where the highest marginal tax rate applies leads to a less residual concave tax schedule.¹⁸ We next show that in most relevant cases in practice, a more residual-concave tax schedule is a more progressive one as is usually defined in the literature on income inequality measurement (see, e.g., Lambert (2001)).

Proposition 2

• Suppose r₁(r₂⁻¹(0))⩾0. Then a tax schedule t₁(x) has more residual progression than t₂(x), that is, [x−t₁(x)]/[x−t₂(x)] is non-increasing for all x, if t₁(x) is more residual-concave than t₂(x).

The condition r₁(r₂⁻¹(0))⩾0, which is equivalent to [x−t₂(x)]=0 implying [x−t₁(x)]⩾0, is clearly satisfied if we only consider tax schedules involving no lump-sum elements, that is, t _i (0)=0, in which case r₁(r₂⁻¹(0))=0. Typical real-world tax schedules with a personal allowance, that is, an amount subtracted from pre-tax income in arriving at taxable income, are clearly in this category.

Given Definition 6, Lemmas 2 and 3 immediately imply the following.

Proposition 3

• For a given pre-tax income distribution, let F and G denote the after-tax income distributions under tax schedules t₁(x) and t₂(x), respectively. If t₁(x) is more residual-concave than t₂(x), then G is more skewed to the right than F and m _G >m _F .

For an interpretation of the result, suppose an investor's initial income is non-random and F and G represent the after-tax prospective income distributions given a risky investment under tax schedules t₁(x) and t₂(x), respectively. The result implies that if t₁(x) is more residual-concave than t₂(x), we can decompose the effect on the EU of the change of tax schedules from t₁ to t₂ as in (1)

where F₁(x)≡F(x+μ _F −μ _G ) and . That is, not only does a tax flattening in the form of the change from t₁ to t₂ unequivocablly increase the skewness of the prospective income distribution but how it affects the attractiveness of the investment is completely determined by its effect on the mean, variance, and third moment of the after-tax distribution. Furthermore, assuming skewness preference, such a tax reform increases the attractiveness of the investment compared with a “skewness-neutral” tax reform that achieves the same effects on the mean and the variance of the after-tax income distribution. More specifically, noting the relationship between F₂(x) and F(x), if a tax schedule t₃(x) is such that , then t₃(x) clearly induces an after-tax income distribution equal to F₂(x) (which has the same mean and variance as G(x)) and a tax reform from t₁(x) to t₂(x) clearly makes the investment more attractive compared with the reform from t₁(x) to t₃(x). Since any graduated-rate (i.e., convex) tax schedule is more residual-concave than a proportional tax as remarked earlier, a corollary of this is a formal validation of Tsiang's conjecture if a progressive tax is understood to be a graduated-rate tax: Any graduated-rate tax has a greater adverse effect on the attractiveness of a risky investment than a proportional tax with perfect loss offset that leaves the mean and variance after tax at the same levels.¹⁹

Appendix

Proof of Lemma 2

• (i) Let F̂(x)=F(σ _F x+μ _F ) and Ĝ(x)=G(σ _G x+μ _G ). Then F⁻¹(G(x)) is convex if and only if F̂⁻¹(Ĝ(x)) is convex, which in turn implies and is implied by [F̂⁻¹(Ĝ(x))−x] being convex. F̂ can thus cross Ĝ at most twice. But μ _F̂ =μ _Ĝ and σ _F̂ =σ _Ĝ imply that F̂ cannot cross Ĝ less than twice.

  (ii) Let F̂(x)=F(σ _F x+μ _F ) and Ĝ(x)=G(σ _G x+μ _G ). μ _F̂ =μ _Ĝ and σ _F̂ =σ _Ĝ are equivalent to ∫ _a ^b[Ĝ(y)−F̂(y)]dy=0 and ∫ _a ^b∫₀^y[Ĝ(s)−F̂(s)]dsdy=0 (see Menezes et al. (1980) for a proof). Ĝ crossing F̂ twice first from above implies that ∫ _a ^xĜ(y)dy can cross ∫ _a ^xF̂(y)dy at most once from above, which, together with ∫ _a ^b∫₀^y[Ĝ(s)−F̂(s)]dsdy=0, implies that ∫ _a ^xF̂(y)dy crosses ∫ _a ^xĜ(y)dy once from above and ∫ _a ^x∫₀^y[Ĝ(s)−F̂(s)]dsdy⩾0 for all x. □

Proof of Theorem 1

• If F and G are skewness comparable, then, by Lemma 1, μ _F =μ _G , σ _F ²=σ _G ², and m _F ³=m _G ³ clearly imply F(x)=G(x). (If μ _F =μ _G , σ _F ²=σ _G ², and F(x)≠G(x), then m _F ³≠m _G ³.)

  For the converse, we are to show that if F and G are not skewness comparable, then it is possible that (μ _F ,σ _F ²,m _F ³)=(μ _G ,σ _G ²,m _G ³) and F(x)≠G(x). Let F and G be such that μ _F =μ _G =μ, σ _F ²=σ _G ²=σ², and ∫ _a ^x∫ _a ^y[G(z)−F(z)]dzdy>0 for x◯ and . ²⁰ Since μ _F =μ _G implies ∫ _a ^b[G(y)−F(y)]dy=0 and σ _F ²=σ _G ² together with μ _F =μ _G implies ∫ _a ^b∫ _a ^y[G(s)−F(s)]dsdy=0, repeated integration by parts gives

  

  That is, (μ _F ,σ _F ²,m _F ³)=(μ _G ,σ _G ²,m _G ³) does not imply F=G if F and G are not skewness comparable.□

Proof of Lemma 3

• (i) By Lemma 1, F being more skewed to the right than G implies m _F >m _G . Conversely, if F is not more skewed to the right than G, by skewness comparability, either [F(σ _F x+μ _F )−G(σ _G x+μ _G )] is a downside risk increase or F(σ _F x+μ _F )=G(σ _G x+μ _G ), which implies m _F ³⩽m _G ³.

  (ii) μ _F =μ _G ≡μ, m _F ³=m _G ³, and skewness comparability imply that F(σ _F x+μ)=G(σ _G x+μ) or equivalently . Furthermore, since

  , σ _F >σ _G implies that, for x<μ, and hence F(x)=G(σ _G /σ _F (x−μ)+μ)⩾G(x). and similarly, for x>μ, F(x)⩽G(x). That is, [G(x) → F(x)] is a simple MPS. Conversely if σ _F ⩽σ _G , then by analogous reasoning [G(x) → F(x)] is an MPC or F(x)=G(x) and hence not an MPS.

  (iii) σ _F =σ _G , m _F ³=m _G ³ and skewness comparability imply that F(x)≡G(x+μ _G −μ _F ). μ _F >μ _G clearly then implies that [G(x) → F(x)] is an FSD improvement. Conversely, if μ _F ⩽μ _G , either [G(x) → F(x)] is an FSD deterioration or F(x)=G(x) and hence [G(x) → F(x)] is not an FSD improvement.□

Proof of Proposition 1

• First we know

Second, being Bernoulli distributions, F₁(σ₁x+μ₁) and F₂(σ₂x+μ₂) can cross at most twice, but (7) precludes the case where they cross once because if two distributions with the same mean cross once, then one is an MPS from the other and has a larger variance. That is, to show p₁<p₂ implies that F₂(x) is more skewed to the right than F₁(x), we only need to show p₁<p₂ implies that F₁(σ₁x+μ₁) crosses F₂(σ₂x+μ₂) first from above, that is, (y₁−μ₁)/σ₁<(y₂−μ₂)/σ₂. To see that, suppose p₁<p₂. Then since (6) is equivalent to

if (y₁−μ₁)/σ₁⩾(y₂−μ₂)/σ₂, then

which implies that F₁(σ₁x+μ₁) single-crosses F₂(σ₂x+μ₂) and contradicts (7). Hence, p₁<p₂ implies that (y₁−μ₁)/σ₁<(y₂−μ₂)/σ₂ and F₁(σ₁x+μ₁) crosses F₂(σ₂x+μ₂) exactly twice first from above.

If p₁=p₂, then by (6)

which gives

and thus contradicts (7). That is, p₁=p₂ implies (y₁−μ₁)/σ₁=(y₂−μ₂)/σ₂, which by (6) implies (z₁−μ₁)/σ₁=(z₂−μ₂)/σ₂ and hence F₁(σ₁x+μ₁)=F₂(σ₂x+μ₂).

This completes the proof of both (i) and (ii) because what is shown also implies that if p₁≮p₂, then F₂(x) is not more skewed to the right than F₁(x), and that if p₁≠p₂, then F₁(σ₁x+μ₁)≠F₂(σ₂x+μ₂).

Proof of Proposition 2 Let T(τ)≡r₁(r₂⁻¹(τ)). Then t₁(x) having more residual progression than t₂(x) is equivalent to T(τ)/τ being non-increasing and t₁(x) being more residual-concave than t₂(x) is equivalent to T being concave. T(τ)/τ is non-increasing in τ if

But by the Mean-Value Theorem, for any τ>0, there exists such that

The concavity of T and T(0)⩾0 thus implies

That is, T(τ)/τ is non-increasing in τ. □