Introduction

Quantum machine learning studies the interplay between machine learning and quantum physics1,2,3,4,5,6. In recent years, a number of quantum learning algorithms have been proposed7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22, which may offer potential quantum advantages over their classical counterparts. However, most of these algorithms either depend on a complexity assumption for the rigorous proof of the quantum advantage15, or are out of the limited capabilities for noisy near-term quantum devices7,8,9,10. On the other hand, the difficulty of constructing fault-tolerant and deep quantum circuits motivates the study of machine learning using constant-depth (shallow) quantum circuits. Most of these algorithms assume classical access to data and use variational circuits for learning. Examples along this direction include machine learning based on variational quantum algorithms23,24,25,26,27,28,29,30,31, which train a parameterized shallow quantum circuit with classical optimizers (see Supplementary Note 1 and Supplementary Fig. 1 for a brief introduction). For these experimental-friendly algorithms, however, there is no rigorous proof showing that they have genuine advantages over classical algorithms. These two points raise the essential problem of whether we can rigorously prove an unconditional quantum advantage in machine learning feasible for near-term quantum devices32. Here, we establish a rigorous quantum-classical representation power separation for the supervised learning model with noiseless shallow quantum circuits (as shown in Fig. 1a) and pin down the noise regimes where the quantum-classical separation exists or disappears for shallow-circuit-based learning.

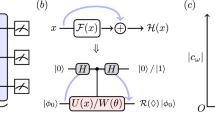
Fig. 1: Illustration of our settings and results.
figure 1

a An illustration of classical and quantum supervised learning models using shallow quantum circuits and neural networks with bounded connectivity. The data samples are first encoded into bit strings x. These bit strings are input into a variational quantum circuit in the quantum-enhanced scenario and a classical neural network in the classical scenario. Each neuron in the classical neural network has bounded connectivity to the neurons in the previous layer. The outputs for two classifiers are distributions on all possible labels encoded in bit strings y. b An implementation of a noisy quantum circuit, where an identical amount p of depolarizing noise is added to each qubit at each step. c The characterization of noise rate regimes for the existence and absence of quantum-classical separation in learning classification tasks defined by shallow quantum circuits. Here, classification tasks R* and RC are relations defined in Theorem 1 and Theorem 2, respectively. The classification task R* can provide a super-polynomial separation in the prediction accuracy when the noise rate is bounded above by O(n−ϵ), while such separation will vanish in the noise regime of \(p \, > \, \Omega (1/\sqrt{\log n})\). In addition, any classification defined by a shallow Clifford circuit possesses no super-polynomial quantum-classical separation when the quantum circuit is implemented with a constant noise rate.

Full size image

Recently, a rigorous and robust quantum advantage in supervised learning has been proved15, which relies on the assumption of the computational hardness in solving the discrete logarithm problem. Despite this exciting progress, an unconditional quantum-classical separation in supervised learning is still lacking. In the quantum computing literature, a different paradigm to rigorously demonstrate quantum advantage was proposed33 to focus on shallow circuits, which is more feasible with noisy devices. It compared the circuit depth required for quantum and classical circuits to solve a relation problem, obtaining a separation originating from the classical hardness of simulating the intrinsic nonlocality property of quantum mechanics. In particular, it is proved that a shallow quantum circuit can solve a relation problem such that any classical circuits with bounded fan-in gates, namely gates with a constant number of input bits, solving this problem with a moderate probability requires a logarithmic depth. Later works extended and amplified this result into an exponential separation in success probability34,35,36,37. Other studies further showed that it is possible to preserve the separation from noises38,39. Very recently, a separation with similar intuition was proposed for sampling problems with shallow circuits40. For classical neural networks, many convolution layers, ReLU layers, and pooling layers satisfy the local connectivity assumptions (i.e., bounded connectivity). Therefore, these unconditional separations provide the intuition that the nonlocality of quantum mechanics can provide an unconditional quantum advantage in machine learning tasks as well.

In this paper, we investigate the separations between shallow variational quantum circuits and classical neural networks for supervised learning tasks. For noiseless quantum devices, we prove that there exists a classification task defined by the input bits and output distributions of a shallow quantum circuit such that any classical neural network with bounded connectivity requires logarithmic depth to output correctly even with exponentially small probability \(\exp (-O({n}^{1-\epsilon }))\), where ϵ is a positive constant and n is the system size. This indicates an unconditional near-optimal separation between the representation power of shallow-circuit-based quantum classifiers and shallow-network-based classical neural networks. This quantum-classical separation originates from the classical hardness of simulating Bell nonlocality41. In addition, we consider a scenario with noises as well (Fig. 1b, c). We show that when the noise rate is bounded above by O(n−ϵ), the quantum-classical separation will persist. On the contrary, if the noise rate exceeds \(\Omega (1/\sqrt{\log n})\), this separation will no longer exist. In addition, we prove that any classification task defined by a noiseless shallow Clifford circuit provides no super-polynomial quantum-classical separation if implemented on quantum devices with a constant noise rate. We will outline our results and leave details to Supplementary Methods.

Results

Generalized classification task

Consider a generalized classification task in the context of supervised learning, where we assign multiple labels \({{{{\bf{y}}}}}_{1},\cdots \,,{{{{\bf{y}}}}}_{K}\in {{{\mathcal{O}}}}\) to an input data sample \({{{\bf{x}}}}\in {{{\mathcal{I}}}}\), with \({{{\mathcal{I}}}}\) and \({{{\mathcal{O}}}}\) denoting the set of all possible samples and labels. Without loss of generality, we encode the samples and labels into bit strings of n and m bits, respectively. In essence, such a classification task can be described by a relation R: {0, 1}n × {0, 1}m → {0, 1}, such that a label y is a legitimate label for an input sample x if and only if R(x, y) = 1. For a supervised learning algorithm, we can also describe the inputs and outputs through a relation (called a hypothesis relation) Rh: {0, 1}n × {0, 1}m → {0, 1}. For an input sample x, we assign Rh(x, y) = 1 if y is a possible output for the learning algorithm and Rh(x, y) = 0 otherwise. Given an input x, the learning algorithm outputs a label y ∈ {0, 1}m with probability Pr[y∣x, Rh]. To evaluate the performance of a learning algorithm, we use a loss function defined as the probability of the learning algorithm outputting a wrong label averaged uniformly over all possible input strings x ∈ {0, 1}n:

$${{{{\mathcal{L}}}}}_{{{{\rm{P}}}}}(R,{R}_{{{{\rm{h}}}}})=1-\frac{1}{{2}^{n}}\sum\limits_{{{{\bf{x}}}},{{{\bf{y}}}}}\Pr [{{{\bf{y}}}}| {{{\bf{x}}}},{R}_{{{{\rm{h}}}}}]{{\mathbb{1}}}_{R({{{\bf{x}}}},{{{\bf{y}}}}) = 1},$$
(1)

where \({{\mathbb{1}}}_{A}\) takes value 1 when the argument A is satisfied and 0 otherwise. We say a relation can be represented by a neural network or a quantum circuit if the loss function can be reduced to zero by choosing a set of suitable variational parameters.

We note that in our setting m can be of the same scale with n, which enables an exponential number of legitimate labels for each input. This generalized classification model fits naturally with the recently flourishing field of computer vision and natural language processing, particularly image segmentation42,43 and sequence-to-sequence learning tasks44 such as text translation45. Take image segmentation for example: the goal is to assign labels to every pixel in an image, which can result in potentially exponentially many valid outputs, especially when certain pixels contain some ambiguity and are allowed to be assigned to even exponentially many labels. Similarly, in translation tasks, there may exist numerous grammatically correct translations, all of which could be considered valid.

Separations for noiseless quantum circuits

We compare the representation power of shallow quantum circuits and shallow classical neural networks equipped with neurons of bounded connectivity. We start with variational quantum circuits without noise. We focus on the qubit encoding scheme throughout this paper for the relation Rh: {0, 1}n × {0, 1}m → {0, 1}. Therefore, the quantum circuit takes n-qubit quantum states as input and output m-bit labels after measurements. In particular, we prove the following theorem, which shows a near-optimal quantum-classical separation between these two types of classifiers.

Theorem 1

There exists a classification task described by a relation R*: {0, 1}n × {0, 1}m → {0, 1} such that a constant-depth parametrized variational quantum circuit with n-qubit input using single- and two-qubit gates can represent this relation (i.e., with zero loss). However, any classical neural network with neurons of bounded connectivity that can represent a hypothesis relation Rh with

$${{{{\mathcal{L}}}}}_{{{{\rm{P}}}}}({R}^{* },{R}_{{{{\rm{h}}}}})\le 1-\exp (-\gamma {n}^{1-\epsilon })$$
(2)

for some constant γ > 0 requires depth at least \(\Omega (\epsilon \log n)\) for any positive constant ϵ < 1.

Proof Sketch

We provide the main idea here. The detailed proof is technically involved and thus left to the Supplementary Note 2. Specifically, we prove the equivalence of the classical circuit model and neural network model with bounded connectivity, and a proposition indicating that there exists an elementary classification task \({R}_{{{{\rm{e}}}}}:{\{0,1\}}^{{n}_{{{{\rm{e}}}}}}\times {\{0,1\}}^{{m}_{{{{\rm{e}}}}}}\to \{0,1\}\) such that there exists a constant-depth quantum circuit that outputs a correct label y for any given sample x with unity probability. Whereas, any (randomized) classical neural network with bounded connectivity outputs correctly with probability at least 1 − α for some constant α requires depth \(\Omega (\log {n}_{{{{\rm{e}}}}})\). We then exploit a direct product of t copies of the relation Re. We show that, by choosing large enough t, one can find a relation \({R}^{* }={R}_{{{{\rm{e}}}}}^{\times t}\) with n = net and m = met to amplify the quantum-classical loss function separation to 0 versus \(1-\exp (-O({n}^{1-\epsilon }))\) for any positive constant ϵ < 1. This completes the proof for Theorem 1.□

We remark that the improved soundness amplification technique, which considers a direct product of t copies of the relation Re, deviates from the argument by Le Gall34 and enables us to push the unconditional separation to near optimal. In particular, while the unconditional separation proved there between classical and quantum circuit is \(1-\exp (-\gamma {n}^{1/2})\) versus 0, we extend this separation to \(1-\exp (-\gamma {n}^{1-\epsilon })\) versus 0 by allowing arbitrary 0 < ϵ < 1. To obtain this result, we push the soundness amplification technique developed by Le Gall34 to its limit by carefully tuning the parameters and refining the procedure.

Theorem 1 can be attributed to the difficulty of simulating quantum nonlocality using classical algorithms46. More concretely, we consider supervised learning the measurement outcomes when measuring each qubit of a well-designed graph state47 on the X-basis or the Y-basis. The graph states contain long cycles, requiring entanglement between distant sites in classical simulation. As a result, any classical neural network with bounded connectivity requires logarithmic depth to connect these distant wires. Similar ideas have been exploited to demonstrate the computational power separation between shallow classical and quantum circuits33,34,35,36,38.

Theorem 1 shows an exponential quantum-classical separation in the success probability of outputting a correct label for the classification task. We note that here the exponential separation is in success probability exclusively, which is different from the typical usage as in35, where the exponential separation refers to both the circuit size and the success probability. This result indicates a quantum-classical separation in the representation power between classical neural networks with bounded connectivity and variational quantum circuits in supervised learning. Shallow quantum circuits are more powerful in representing complicated relations than classical shallow neural networks. Our results indicate the existence of some relation that can be represented by a constant-depth quantum circuit but not by any constant-depth neural networks with bounded connectivity however one tunes the parameters in a rigorous fashion. Whether one can efficiently optimize the parameters in the variational quantum circuit to find this function is an independent and challenging question that warrants further investigation. In addition, this separation also implies a constant-versus-logarithmic time separation in the inference stage of the classification task, between quantum classifiers based on constant-depth variational circuits and classical classifiers based on neural networks with bounded connectivity.

Furthermore, we rigorously prove that there exists a classical neural network of depth \({c}_{0}\log n\) with bounded connectivity and fine-tuned parameters that can reduce the loss function to \(1-\exp (-O(n/\sqrt{\log n}))\) for any relation defined by a two-dimensional shallow quantum circuit (see Supplementary Note 3). Therefore, the quantum-classical separation shown in Theorem 1 is near-optimal. In particular, to prove the optimality we explicitly propose an algorithm. This algorithm divides the input qubits into blocks of \(O(\sqrt{\log n})\times O(\sqrt{\log n})\) qubits. We show that for shallow quantum circuits with single- and two-qubit gates, a classical simulation can output correctly if there are no inter-block gates. We then prove that the number of qubits in the input string affected by inter-block gates is bounded above by \(O(n/\sqrt{\log n})\). Therefore, this classical simulation can output a correct string for all the qubits except the affected qubits. Finally, we apply a random guessing strategy on these affected qubits, and the probability of outputting a correct string is thus \(\exp (-O(n/\sqrt{\log n}))\).

Theorem 1 can be extended straightforwardly to loss functions other than that defined in Eq. (1). For example, we consider the loss function defined on R* and Rh based on the widely used Kullback-Leibler (KL) divergence48. In Supplementary Note 3, we show that relation R* in Theorem 1 outputs according to an equal distribution on all possible strings y. If we compute the KL divergence between R* and the probability distribution output from a learning algorithm, the loss function for the variational quantum circuit can be reduced to zero. However, any classical neural network with bounded connectivity and loss function smaller than O(n1−ϵ) requires depth \(\Omega (\epsilon \log n)\).

Noisy quantum circuits

Short-term quantum devices suffer from noises32. As a result, a question of both theoretical and experimental interest is whether the quantum-classical separation discussed above persists for noisy quantum circuits. It is shown that the existence of noise leads to the ineffectiveness of deep quantum circuits caused by the barren plateau phenomenon49,50,51,52. However, the impact of noises on shallow circuits in the average case remains largely unexplored. To address this important question, we focus on the depolarization noise model53\(\rho \to (1-p)\rho +\frac{p}{3}(X\rho X+Y\rho Y+Z\rho Z)\) for the shallow quantum circuit as an example. We prove that the variational quantum circuits in Theorem 1 suffering from noise rate p can only output correctly with probability \(\exp (-\Theta (pn))\). Therefore, we conclude that the quantum-classical separation in Theorem 1 remains when p = O(n−ϵ). Although both the classical and quantum success probabilities are exponentially decaying within this regime, these two probabilities decay with different rates of \(\exp (-{n}^{\epsilon })\) and \(\exp (-pn)\), which yields a super-polynomial separation. However, the noise rate on most near-term quantum devices without any error mitigation or correction is typically assumed to be p = O(1)32,54,55,56. In such a scenario, we rigorously prove that the separation in Theorem 1 vanishes. In the above discussion, we have proposed a classical algorithm (see Supplementary Fig. 2 for illustration) using logarithmic depth to output a correct label of a shallow quantum circuit with probability at least \(\exp (-O(n/\sqrt{\log n}))\) when proving the near-optimality of the noiseless quantum-classical separation. By comparing this result and the performance bound for noisy shallow quantum circuits, the largest noise threshold for this quantum-classical separation will not exceed \(p=O(1/\sqrt{\log n})\), which decreases as the system size increases. An illustrative figure for the noise regimes where the quantum-classical separation exists or disappears for shallow-circuit-based learning is provided as Fig. 1(b). We leave the details for the derivation of the upper and lower bound on the noise threshold for demonstrating Theorem 1 on noisy devices in Supplementary Note 3.

We further find that the nonexistence of quantum-classical separation in the context of supervised learning using shallow circuits can be extended to more general cases. In particular, we derive the following theorem showing that there is no super-polynomial quantum-classical separation between noisy shallow variational quantum circuits and classical learning algorithms using shallow neural networks or circuits.

Theorem 2

For any classification task corresponding to a relation RC: {0, 1}n × {0, 1}m → {0, 1} that can be defined by a (classically-controlled) Clifford circuit of any depth, no quantum circuit undergoing the depolarization noise ρ → (1 − p)ρ + p(XρX + YρY + ZρZ)/3 with constant noise rate p can achieve a loss less than

$$1-{(1-{{{{\mathcal{L}}}}}_{{{{\rm{P}}}}}({R}_{{{{\rm{C}}}}},{R}_{{{{\rm{r}}}}}))}^{{\log }_{2}\frac{1}{1-\frac{2}{3}p}},$$
(3)

where Rr is the relation represented by a classical neural network that outputs uniformly randomly over y ∈ {0, 1}m.

Proof Sketch

We sketch the major steps here and leave the technical details to Supplementary Note 4. We adapt a well known lemma57,58 and prove that the output of the quantum circuit defining RC uniformly distributes over an affine subspace of \({{\mathbb{Z}}}_{2}^{m}\). Therefore, there exists a subset yS of output bits such that when the input bits and the output bits outside of yS are fixed, only one assignment of the bits in yS can satisfy RC, meaning that the probability of success for a classical random guessing algorithm is \({(\frac{1}{2})}^{| {{{{\bf{y}}}}}_{S}| }\). Similarly, for noisy quantum circuits, we consider the noise in the layer exactly before measuring the bits in yS conditioned on all other noises. We conclude that the output label for a noisy quantum circuit for RC is correct with probability at most \({(1-\frac{2}{3}p)}^{| {{{{\bf{y}}}}}_{S}| }\). This completes the proof for this theorem. □

We recall that the shallow variational quantum circuit in Theorem 1 contains non-Clifford gates. However, it can be proved that this classification task can also be represented by a classically-controlled Clifford quantum circuit34. Thus, the result in Theorem 2 also works for the classification task in Theorem 1. As p is a constant, \({\log }_{2}(1/(1-2p/3))\) is a constant. Therefore, Theorem 2 shows that the success probability for a noisy shallow quantum circuit to output a correct label for any classification task defined by a noiseless shallow Clifford circuit scale at most polynomially as that of a classical algorithm that randomly guesses the labels. Since random guesses can be accomplished by a classical neural network of constant depth, the separation in Theorem 1 does not exist here. Theorem 2 further indicates that we cannot expect a near-term experimental demonstration of quantum advantage only using classification tasks characterized by a Clifford circuit.

We note that Theorem 2 is a strong no-go theorem that applies to any relations defined by Clifford circuits of arbitrary depth. The noise model that applies also holds for not only the standard independent and identically distributed depolarization noise at each layer (as shown in Fig. 1(b)), but also holds for even if the depolarizing noise happens only at the last layer (see Supplementary Note 4 for details). It is worthwhile to remark that the relation considered in Theorem 2 can be defined by a noiseless Clifford quantum circuit, which is different from the relations considered in works by Bravyi et al. and Grier et al.38,39. There, an implicit error correction technique is introduced to guarantee that the quantum-classical separation persists for noisy circuits. Such a technique takes a problem with a separation between classical circuits and noiseless quantum circuits and encodes the problem in error-correcting codes. Then the error syndromes are measured without carrying out the error correction and the classical circuit is required to do the same. This yields a separation between shallow classical circuits and noisy quantum circuits of constant noise rate. Therefore, the resulting relation can be represented but not defined by a shallow quantum circuit as the quantum circuit is allowed to make a mistake with a moderate probability. Whereas, in our scenario, the output distribution of the relation is assumed to be exactly the same with some quantum circuits, yielding a more restricted class of relations. We conclude that this kind of restriction is vital for the nonexistence of the separation in works by Bravyi et al. and Grier et al.38,39.

We also clarify the differences between Theorem 2 and the recent results by Aharonov et al.55 in the absence of quantum advantage on constant-rate noisy random circuit sampling. Aharonov el al.55 considered the task aiming at approximating the output distribution of a random quantum circuit within a small total variational difference. It is widely believed that classically simulating the output distributions of a (noisy) random circuit of logarithmic depth exactly is difficult17,59,60,61,62,63,64, but Aharonov el al.55 explicitly propose an efficient algorithm to approximate the outputs distribution of noisy random circuits with polynomial complexity. While this result gives evidence against the quantum advantage of random circuit sampling with a constant noise rate, Theorem 2 focus on the classification task represented by quantum circuits of depth O(1). The random circuits are assumed to satisfy the anti-concentration condition, which requires a circuit depth of \(\Omega (\log n)\), while we consider shallow circuits of constant depth. It is hard to classically simulate the result of random circuits, but the output distribution of the shallow quantum circuit considered in this paper can be efficiently simulated by classical algorithms65,66. To construct a quantum-classical separation in this regime, we compare the representation power of shallow quantum circuits to that of shallow classical neural networks and show the quantum-classical separation. We prove that classification tasks defined by shallow Clifford circuits can not demonstrate any super-polynomial quantum advantage on near-term devices with constant noise rates.

Discussion

Many questions remain and are worth further investigation. For instance, our discussion in this paper focused on the relation exactly defined by a shallow quantum circuit. For quantum devices with a constant noisy rate, it is still possible to find a quantum-classical separation in the success probability for relations not exactly defined by a quantum circuit. How to explicitly construct such a hard classification task to rigorously obtain a noise-tolerant quantum-classical separation without relying on quantum error correction is crucial for demonstrating quantum advantages with near-term quantum devices. In practice, many classical neural networks bear unbounded connectivity. How to extend our results to this scenario demands further exploration. One may also explore the potential representation power trade-off between width and depth for classical neural networks with unbounded connectivity. In addition, how to extend our results to unsupervised learning and reinforcement learning scenarios remains unclear. Whether we can transfer our separation in representation power to a separation in sample complexity or computational complexity is an important future direction as well. Finally, it would be of both fundamental and practical importance to carry out an experiment to demonstrate the unconditional quantum-classical separation proved in Theorem 1. This would be a far-reaching step towards practical quantum learning supremacy in the future.