On the sample complexity of quantum Boltzmann machine learning

Abstract

Quantum Boltzmann machines (QBMs) are machine-learning models for both classical and quantum data. We give an operational definition of QBM learning in terms of the difference in expectation values between the model and target, taking into account the polynomial size of the data set. By using the relative entropy as a loss function, this problem can be solved without encountering barren plateaus. We prove that a solution can be obtained with stochastic gradient descent using at most a polynomial number of Gibbs states. We also prove that pre-training on a subset of the QBM parameters can only lower the sample complexity bounds. In particular, we give pre-training strategies based on mean-field, Gaussian Fermionic, and geometrically local Hamiltonians. We verify these models and our theoretical findings numerically on a quantum and a classical data set. Our results establish that QBMs are promising machine learning models.

Introduction

Machine learning (ML) research has developed into a mature discipline with applications that impact many different aspects of society. Neural network and deep learning architectures have been deployed for tasks such as facial recognition, recommendation systems, time series modeling, and for analyzing highly complex data in science. In addition, unsupervised learning and generative modeling techniques are widely used for text, image, and speech generation tasks, which many people encounter regularly via interaction with chatbots and virtual assistants. Thus, the development of new machine learning models and algorithms can have significant consequences for a wide range of industries and, more generally, society as a whole¹.

Recently, researchers in quantum information science have asked the question of whether quantum algorithms can offer advantages over conventional machine learning algorithms. This has led to the development of quantum algorithms for gradient descent, classification, generative modeling, reinforcement learning, as well as many other tasks^2,3,4,5,6. However, one cannot straightforwardly generalize results from the conventional ML realm to the quantum ML realm. One must carefully reconsider the data encoding, training complexity, and sampling in the quantum machine learning (QML) setting. For example, it is yet unclear how to efficiently embed large data sets into quantum states so that a genuine quantum speedup is achieved^7,8. Furthermore, as quantum states prepared on quantum devices can only be accessed via sampling, one cannot estimate properties with arbitrary precision. This gives rise to new problems, such as barren plateaus^{9,10,11,12,13,14}, that make the training of certain QML models challenging or even practically impossible.

In this work, we show that a particular quantum generative model, the quantum Boltzmann machine^15,16,17,18 (QBM) without hidden units, does not suffer from these issues, and can be trained with polynomial sample complexity on future fault-tolerant quantum computers. QBMs are physics-inspired ML models that generalize the classical Boltzmann machines to quantum Hamiltonian ansätze. The Hamiltonian ansatz is defined on a graph where each vertex represents a qubit and each edge represents an interaction. The task is to learn the strengths of the interactions, such that samples from the quantum model mimic samples from the target data set. Quantum generative models of this kind could find use in ML for science problems, by learning approximate descriptions of the experimental data. QBMs could also play an important role as components of larger QML models^{19,20,21,22,23}. This is similar to how classical Boltzmann machines can provide good weight initializations for the training of deep neural networks²⁴. One advantage of using a QBM over a classical Boltzmann machine is that it is more expressive since the Hamiltonian ansatz can contain more general non-commuting terms. This means that in some settings, the QBM outperforms its classical counterpart, even for classical target data¹⁸. Here we focus on QBMs without hidden units since their inclusion leads to additional challenges^12,25,26, and there exists no evidence that they are beneficial.

In order to obtain practically relevant results, we begin by providing an operational definition of QBM learning. Instead of focusing on an information-theoretic measure, we assess the QBM learning performance by the difference in expectation values between the target and the model. We require that the data set and model parameters can be efficiently stored in classical memory. This means that the number of training data points is polynomial in the number of features if the target is classical, or in the number of particles if the target is quantum. Thus, statistics computed from such data set have polynomial precision. We then employ stochastic gradient descent methods^27,28 in combination with shadow tomography^29,30,31 to prove that QBM learning can be solved with polynomially many evaluations of the QBM model. Each evaluation of the model requires the preparation of one Gibbs state, and therefore, in this paper, we refer to the sample complexity as the required number of Gibbs state preparations. We also prove that the required number of Gibbs samples is reduced by pre-training on a subset of the parameters. This means that classically pre-training a simpler QBM model can potentially reduce the (quantum) training complexity. For instance, we show that one can analytically pre-train a mean-field QBM and a Gaussian Fermionic QBM in closed form. In addition, we show that one can pre-train geometrically local QBMs with gradient descent, which has some improved performance guarantees. To the best of our knowledge, this is the first time these exactly solvable models are used for either training or pre-training QBMs.

It is important to note that the time complexity of preparing and estimating properties of Gibbs states at finite temperature is largely unknown, but can be exponential in the worst case³². For cases where the Gibbs state preparation is intractable, the polynomial sample complexity of QBM learning becomes irrelevant as obtaining one sample already takes exponential time. On the other hand, the polynomial sample complexity is a prerequisite for efficient learning which many other QML models do not share. In this work, we are only concerned with the sample complexity of the QBM learning problem, and we do not discuss any specific Gibbs sampling implementation. We shall mention in passing that Gibbs states satisfying certain locality constraints can be efficiently simulated by classical means, e.g., using tensor networks^33,34. Furthermore, generic Gibbs states can be prepared and sampled on a quantum computer by a variety of methods (e.g., see refs. ^{35,36,37,38,39,40,41,42,43}), potentially with a quadratic speedup over classical algorithms. There also exist hybrid quantum-classical variational algorithms for Gibbs state preparation^{44,45,46,47,48,49}, but there are currently many open issues regarding their trainability^9,11,14,50. In practice, QBM learning allows for great flexibility in model design and can be combined with almost any Gibbs sampler.

Throughout the paper, we compare QBM learning and a related, but crucially different, problem called Hamiltonian learning^{31,51,52,53,54,55}. Learning the Hamiltonian of a physical system in thermal equilibrium can be thought of as performing quantum state tomography. This has useful applications, for example, in the characterization of quantum devices, but requires prior knowledge about the target system and suffers an unfavorable scaling with respect to the temperature⁵³. In contrast, the aim of QBM learning is to produce a generative model of the data at hand, with the Hamiltonian playing the role of an ansatz.

Our setup and theoretical results are summarized in Fig. 1. We provide classical numerical simulation results in Figs. 2 and 3 which confirm our analytical findings. We then conclude the paper with a discussion of the generalization capability of QBMs and avenues for future work.

Fig. 1: Summary of the results.

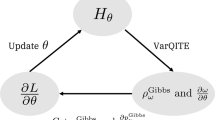
The quantum Boltzmann machine (QBM) learning algorithm takes as input a data set of size polynomial in the number of features/qubits, and an ansatz with parameters θ and a set of m Hermitian operators {H_i}. In Definition 1, we provide an operational definition of the QBM learning problem where the model and target expectations must be close to within polynomial precision ϵ. A solution θ^opt is guaranteed to exist by Jaynes' principle. With Theorems 1 and 2, we establish that QBM learning can be solved by minimizing the quantum relative entropy S(η∥ρ_θ) with respect to θ using stochastic gradient descent (SGD). This requires a polynomial number of iterations T, each using a polynomial number of Gibbs state preparations, i.e., the sample complexity is polynomial. With Theorem 3, we prove that pre-training strategies that optimize a subset ${\theta }^{{{\rm{pre}}}}$ of the QBM parameters are guaranteed to lower the initial quantum relative entropy. After training, the QBM can be used to generate new synthetic data. Icons by SVG Repo, used under CC0 1.0 and adapted for our purpose.

Fig. 2: Pre-training and training quantum Boltzmann machines.

a Quantum relative entropy $S(\eta | {\rho }_{{\theta }^{{{\rm{pre}}}}})$ obtained after various pre-training strategies. We compare a mean-field (MF) model, a one-dimensional and two-dimensional geometrically local (GL) model, and a Gaussian Fermionic (GF) model to no pre-training/maximally mixed state. For the GL models, we stop the pre-training after the pre-training gradient is smaller than 0.01. We consider an 8-qubit target η as the Gibbs state ${e}^{{{{\mathcal{H}}}}_{{{\rm{XXZ}}}}}/Z$ of a one-dimensional XXZ model (Quantum Data), and a target η which coherently encodes the binary salamander retina data set (Classical Data). b Quantum relative entropy versus number of iterations for Quantum Data. The t < 0 iterations (gray area) show the reduction in relative entropy for GL 2D pre-training (red line). The t = 0 iteration corresponds to the pre-training results in panel (a). The t > 0 iterations show the training results in the absence of gradient noise, i.e., κ = ξ = 0.

Methods

We start by formally setting up the quantum Boltzmann machine (QBM) learning problem. We give the definitions of the target and model and describe how to assess performance by the precision of the expectation values. These definitions and assumptions are key to our results, and we introduce and motivate them here carefully. To further motivate our problem definition we compare to other related problems in the literature, such as quantum Hamiltonian learning.

We consider an n-qubit density matrix η as the target of the machine learning problem. If the target is classical, n could represent the number of features, e.g., the pixels in black-and-white pictures, or more complex features that have been extracted and embedded in the space of n qubits. If the target is quantum, n could represent the number of spin-$\frac{1}{2}$ particles, but again, more complex many-body systems can be embedded in the space of n qubits. In the literature, it is often assumed that algorithms have direct and simultaneous access to copies of η. We do not take that path here. Instead, we consider a setup where one only has access to classical information about the target. We have a data set ${{\mathcal{D}}}=\{{s}^{\mu }\}$ of data samples s^μ and, crucially, we assume the data set can be efficiently stored in a classical memory: the amount of memory required to store each data sample is polynomial in n, and there are polynomially many samples. For example, s^μ can be bitstrings of length n; this includes data sets like binary images and time series, categorical and count data, or binarized continuous data. As another example, the data may originate from measurements on a quantum system. In this case, s^μ identifies an element of the positive operator-valued measure describing the measurement.

Next, we define the machine learning model which we use for data fitting. The fully visible QBM is an n-qubit mixed quantum state of the form

$${\rho }_{\theta }=\frac{{e}^{{{{\mathcal{H}}}}_{\theta }}}{Z},$$

(1)

where $Z={{\rm{Tr}}}[{e}^{{{{\mathcal{H}}}}_{\theta }}]$ is the partition function. The parameterized Hamiltonian is defined as

$${{{\mathcal{H}}}}_{\theta }=\mathop{\sum }\limits_{i=1}^{m}{\theta }_{i}{H}_{i},$$

(2)

where $\theta \in {{\mathbb{R}}}^{m}$ is the parameter vector, and {H_i} is a set of m Hermitian and orthogonal operators acting on the 2ⁿ-dimensional Hilbert space. For example, these could be n-qubit Pauli operators. As the true form of the target density matrix is unknown, the choice of operators {H_i} in the Hamiltonian is an educated guess. It is possible that, once the Hamiltonian ansatz is chosen, the space of QBM models does not contain the target, i.e., ρ_θ ≠ η, ∀ θ. This is called a model mismatch, and it is often unavoidable in machine learning. In particular, since we require m to be polynomial in n, ρ_θ cannot encode an arbitrary density matrix. Note that for fixed parameters, ρ_θ is also known as Gibbs state in the literature. Thus, we refer to an evaluation of the model as the preparation of a Gibbs state.

A natural measure to quantify how well the QBM ρ_θ approximates the target η is the quantum relative entropy

$$S(\eta \!\!\parallel \!\!{\rho }_{\theta })={{\rm{Tr}}}[\eta \log \eta ]-{{\rm{Tr}}}[\eta \log {\rho }_{\theta }].$$

(3)

This measure generalizes the classical Kullback-Leibler divergence to density matrices. The relative entropy is exactly zero when the two densities are equal, η = ρ_θ, and S > 0 otherwise. In addition, when S(η∥ρ_θ) ≤ ϵ, by Pinsker’s inequality, all Pauli expectation values are within ${{\mathcal{O}}}(\sqrt{\epsilon })$. However, achieving this is generally not possible due to the model mismatch. In theory, one can minimize the relative entropy in order to find the optimal model parameters ${\theta}^{{{\rm{opt}}}}={{{\rm{argmin}}}}_{\theta}S(\eta \!\!\parallel \!\!{\rho}_{\theta })$. The form of the partial derivatives can be obtained analytically and reads

$$\frac{\partial S(\eta \!\!\parallel \!\!{\rho }_{\theta })}{\partial {\theta }_{i}}={\langle {H}_{i}\rangle }_{{\rho }_{\theta }}-{\langle {H}_{i}\rangle }_{\eta }.$$

(4)

This is the difference between the target and model expectation values of the operators that we choose in the ansatz. A stationary point of the relative entropy is obtained when ${\langle {H}_{i}\rangle }_{{\rho }_{\theta }}={\langle {H}_{i}\rangle }_{\eta }$ for i ∈ {1, …, m}. Since S is strictly convex (see Supplementary Note 2), this stationary point is the unique global minimum.

It is difficult in practice to quantify how well the QBM is trained by means of relative entropy. In order to accurately estimate S(η∥ρ_θ), one requires access to the entropy of the target and the partition function of the model. Moreover, due to the model mismatch, the optimal QBM may have $S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{{{\rm{opt}}}}}) \, > \, 0$, which is unknown beforehand. In this work, we provide an operational definition of QBM learning based on the size of the gradient  ∇S(η∥ρ_θ).

Definition 1 (QBM learning problem)

Given a polynomial-space data set {s^μ} obtained from an n-qubit target density matrixη, a target precisionϵ > 0, and a fully visible QBM with Hamiltonian${{{\mathcal{H}}}}_{\theta }={\sum }_{i = 1}^{m}{\theta }_{i}{H}_{i}$, find a parameter vectorθsuch that with high probability

$$| {\langle {H}_{i}\rangle }_{{\rho }_{\theta }}-{\langle {H}_{i}\rangle }_{\eta }| \le \epsilon ,\qquad \forall i.$$

(5)

The expectation values of the target can be obtained from the data set in various ways. For example, for the generative modeling of a classical binary data set one can define a pure quantum state and obtain its expectation values (see Kappen¹⁸ and Supplementary Note 5). For the modeling of a target quantum state (density matrix) one can estimate expectation values from the outcomes of measurements performed in different bases. Due to the polynomial size of the data set, we can only compute the properties of the target (and model) to finite precision. For example, suppose that s^μ are data samples from some unknown probability distribution P(s) and that we are interested in the sample mean. An unbiased estimator for the mean is $\hat{s}=\frac{1}{M}\mathop{\sum }_{\mu = 1}^{M}{s}^{\mu }$. The variance of this estimator is σ²/M, where σ² is the variance of P(s). By Chebyshev’s inequality, with high probability, the estimation error is of order $\sigma /\sqrt{M}$. The polynomial size of the data set implies that the error decreases polynomially in general. In light of this, we say the QBM learning problem is solved for any precision ϵ > 0 in Eq. (5). The idea is that the expectation values of the QBM and target should be close enough that one cannot distinguish them without enlarging the data set.

An exact solution to the QBM learning problem always exists by Jaynes’ principle⁵⁶: given a set of target expectations $\{{\langle {H}_{i}\rangle }_{\eta }\}$ there exists a Gibbs state ${\rho }_{{\theta }^{{{\rm{opt}}}}}={e}^{{\sum }_{i}{\theta }_{i}^{{{\rm{opt}}}}{H}_{i}}/Z$ such that $| {\langle {H}_{i}\rangle }_{{\rho }_{{\theta }^{{{\rm{opt}}}}}}-{\langle {H}_{i}\rangle }_{\eta }| =0,\forall i$. We refer to the model corresponding to Jaynes’ solution θ^opt as the optimal model. In QBM learning, we try to get as close as possible to this optimal model by minimizing the difference in expectation values. As shown in Supplementary Note 3, any solution to the QBM learning problem implies a bound on the optimal relative entropy, namely

$$S(\eta \!\!\parallel \!\!{\rho }_{\theta })-S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{{{\rm{opt}}}}})\le 2\epsilon \parallel \!\!\theta -{\theta }^{{{\rm{opt}}}}{\parallel }_{1}.$$

(6)

A similar result can be derived from Proposition A2 in Rouzé and França³¹. This means that if one can solve the QBM learning problem to precision $\epsilon \le \frac{{\epsilon }^{{\prime} }}{2\parallel \theta -{\theta }^{{{\rm{opt}}}}{\parallel }_{1}}$, one can also solve a stronger learning problem based on the relative entropy to precision ${\epsilon }^{{\prime} }$. However, this requires bounding ∥θ − θ^opt∥₁.

We further motivate our problem definition by highlighting important differences with a related problem called quantum Hamiltonian learning^{31,51,52,53,54,55}. This problem can be understood as trying to find a parameter vector ∥θ − θ^*∥₁ ≤ ϵ, where θ^* is the true parameter vector defining a target Gibbs state η. This is, in fact, a stronger version of the QBM learning problem because finding the true parameters, θ^*, is more demanding than getting ϵ-close to the expectation values of the optimal model from Jaynes’ solution. In realistic machine learning settings, we do not know the exact form of η a priori, and Hamiltonian learning is, in effect, equivalent to quantum state tomography. This task has an exponential sample-complexity lower bound²⁹. Moreover, even if we do know the exact form, minimizing the distance to the true parameters, ∥θ − θ^*∥₁, can make the problem significantly more complicated than QBM learning, and potentially impractical to solve. Consider a single-qubit target $\eta ={e}^{{{{\mathcal{H}}}}^{* }}/{{\rm{Tr}}}[{e}^{{{{\mathcal{H}}}}^{* }}]$, with Hamiltonian ${{{\mathcal{H}}}}^{* }={\theta }^{* }{\sigma }^{z}$. We can easily see that near ${\langle {\sigma }^{z}\rangle }_{\eta }=1-\epsilon$ the parameter θ^* diverges. For example, if θ^* = 2.64 then ${\langle {\sigma }^{z}\rangle }_{\eta }=0.99$ and if θ^* = 3.8 then ${\langle {\sigma }^{z}\rangle }_{\eta }=0.999$, from which we see that the optimal parameter is very sensitive, ${{\mathcal{O}}}(1)$, to small changes, ${{\mathcal{O}}}(1{0}^{-2})$, in expectation values. In these cases, Hamiltonian learning is much harder than simply finding a QBM whose expectation value is within ϵ. A similar argument can be made for high-temperature targets near the maximally mixed state. Here the QBM problem is trivial: since all target expectations are ${\langle {H}_{i}\rangle }_{\eta }\approx {2}^{-n}{{\rm{Tr}}}[{H}_{i}]$, any model sufficiently close to the maximally mixed state solves the QBM learning problem. In contrast, Hamiltonian learning insists on estimating the unique true parameters.

Let us now discuss a method for solving QBM learning. We approach the problem by iteratively minimizing the quantum relative entropy, Eq. (3), by stochastic gradient descent (SGD)²⁸. This method requires access to a stochastic gradient ${\hat{g}}_{{\theta }^{t}}$ computed from a set of samples at time t. Recall that our gradient has the form given in Eq. (4). The expectations with respect to the target are estimated from a random subset of the data, often called a mini-batch. The mini-batch size is a hyper-parameter and determines the precision ξ of each target expectation. Similarly, the QBM model expectations are estimated from measurements, for example, using classical shadows^29,30 of the Gibbs state ${\rho }_{{\theta }^{t}}$ approximately prepared on a quantum device⁴³. The number of measurements is also a hyper-parameter and determines the precision κ of each QBM expectation. We assume that the stochastic gradient is unbiased, i.e., ${\mathbb{E}}[\, {\hat{g}}_{{\theta }^{t}}]=\nabla S(\eta \!\!\parallel \!\!{\rho }_{\theta }){| }_{\theta = {\theta }^{t}}$, and that each entry of the vector has bounded variance. At iteration t, SGD updates the parameters as

$${\theta }^{t+1}={\theta }^{t}-{\gamma }^{t}{\hat{g}}_{{\theta }^{t}},$$

(7)

where γ^t is called the learning rate.

Results

Sample complexity

Stochastic gradient descent solves the QBM learning problem with polynomial sample complexity. We state this in the following theorem, which is the main result of our work.

Theorem 1 (QBM training)

Given a QBM defined by a set ofn-qubit Pauli operators ${\{{H}_{i}\}}_{i = 1}^{m}$, a precisionκ for the QBM expectations, a precision ξ for the data expectations, and a target precision ϵ such that ${\kappa }^{2}+{\xi }^{2}\ge \frac{\epsilon }{2m}$. After

$$T=\frac{48{\delta }_{0}{m}^{2}({\kappa }^{2}+{\xi }^{2})}{{\epsilon }^{4}}$$

(8)

iterations of stochastic gradient descent on the relative entropy S(η∥ρ_θ) with constant learning rate ${\gamma }^{t}=\frac{\epsilon }{4{m}^{2}({\kappa }^{2}+{\xi }^{2})}$, we have

$${\min }_{t = 1,..,T}\ {\mathbb{E}}| {\langle {H}_{i}\rangle }_{{\rho }_{{\theta }^{t}}}-{\langle {H}_{i}\rangle }_{\eta }| \le \epsilon ,\qquad \forall i,$$

(9)

where ${\mathbb{E}}[\cdot ]$ denotes the expectation with respect to the random variable θ^t. Each iteration t ∈ {0, …, T} requires

$$N\in {{\mathcal{O}}}\left(\frac{1}{{\kappa }^{4}}\log \frac{m}{1-{\lambda }^{\frac{1}{T}}}\right)$$

(10)

preparations of the Gibbs state ${\rho }_{{\theta }^{t}}$, and the success probability of the full algorithm is λ. Here,${\delta }_{0}=S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{0}})-S(\eta \! \! \parallel \! \! {\rho }_{{\theta }^{{{\rm{opt}}}}})$ is the relative entropy difference with the optimal model ${\rho }_{{\theta }^{{{\rm{opt}}}}}$.

A detailed proof of this theorem is given in Supplementary Note 3. It consists of carefully combining three important observations and results. First, we show that the quantum relative entropy for any QBM ρ_θ is L-smooth with $L=2m{\max }_{j}\parallel \!\!{H}_{j}{\parallel }_{2}^{2}$, which follows from upper bounding the relative entropy and quantum belief propagation⁵⁷. A similar result can be found in Rouzé and França³¹, Proposition A4. This is then combined with SGD convergence results from the machine learning literature^27,28 to obtain the number of iterations T. Finally, we use sampling bounds from quantum shadow tomography to obtain the number of preparations N. In this last step, we focus on the shadow tomography protocol in Huang et al.³⁰, which restricts our result to Pauli observables H_i ≡ P_i, thus ∥H_i∥₂ = 1. It is possible to extend this to generic two-outcome observables^29,58 with a polylogarithmic overhead compared to Eq. (10). Furthermore, for k-local Pauli observables, we can improve the result to

$$N\in {{\mathcal{O}}}\left(\frac{{3}^{k}}{{\kappa }^{2}}\log \frac{m}{1-{\lambda }^{\frac{1}{T}}}\right)$$

(11)

with classical shadows constructed from randomized measurement⁵⁹ or by using pure thermal shadows⁴³.

By combining Eqs. (8) and (10), we see that the final number of Gibbs state preparations N_tot ≥ T × N scales polynomially with m, the number of terms in the QBM Hamiltonian. By our classical memory assumption, we can only have $m\in {{\mathcal{O}}}({{\rm{poly}}}(n))$. This means that the number of required measurements to solve QBM learning scales polynomially with the number of qubits. Consequently, there are no barren plateaus in the optimization landscape for this problem, resolving an open question from the literature^26,50 for QBMs without hidden units. Furthermore, also the stronger problem in Eq. (6) can be solved without encountering an exponentially vanishing gradient as we show in Supplementary Note 3.

We remark, however, that our result does not imply a solution to the stricter Hamiltonian learning problem with polynomially many samples. In order to achieve this one needs some stronger conditions. For example, using α-strong convexity for the specific case of geometrically local models, as shown in Anshu et al.⁵³. In Supplementary Note 2, we investigate generalizing this by looking at generic Hamiltonians made of low-weight Pauli operators. We perform numerical simulations using differentiable programming⁶⁰ and find evidence indicating that, even in this case, the quantum relative entropy is α-strong convex. This means we could potentially achieve an improved sample complexity for QBM learning. We prove the following theorem in Supplementary Note 3.

Theorem 2 (α-strongly convex QBM training)

Given a QBM defined by a Hamiltonian ansatz${{{\mathcal{H}}}}_{\theta }$such thatS(η∥ρ_θ) isα-strongly convex, a precision κ for the QBM expectations, a precision ξ for the data expectations, and a target precisionϵ such that${\kappa }^{2}+{\xi }^{2}\ge \frac{\epsilon }{2m}$. After

$$T=\frac{18{m}^{2}({\kappa }^{2}+{\xi }^{2})}{{\alpha }^{2}{\epsilon }^{2}}$$

(12)

iterations of stochastic gradient descent on the relative entropyS(η∥ρ_θ) with learning rate${\gamma }^{t}\le \frac{1}{4{m}^{2}}$, we have

$$\mathop{\min }_{t = 1,..,T}\ {\mathbb{E}}| {\langle {H}_{i}\rangle }_{{\rho }_{{\theta }^{t}}}-{\langle {H}_{i}\rangle }_{\eta }| \le \epsilon ,\qquad \forall i.$$

(13)

Each iteration requires the number of samples given in Eq. (10).

Finally, we observe that the sample bound in Theorem 1 depends on δ₀, the relative entropy difference of the initial and optimal QBMs. This means that if we can lower the initial relative entropy with an educated guess, we also tighten the bound on the QBM learning sample complexity. In this respect, we prove that we can reduce δ₀ by pre-training a subset of the parameters in the Hamiltonian ansatz. Thus, pre-training reduces the number of iterations required to reach the global minimum.

Theorem 3 (QBM pre-training)

Assume a targetηand a QBM model${\rho }_{\theta }={e}^{{\sum }_{i = 1}^{m}{\theta }_{i}{H}_{i}}/Z$ for which we like to minimize the relative entropyS(η∥ρ_θ). Initializingθ⁰ = 0 and pre-trainingS(η∥ρ_θ) with respect to any subset of$\tilde{m}\le m$ parameters guarantees that

$$S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{{{\rm{pre}}}}})\le S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{0}}),$$

(14)

where ${\theta }^{{{\rm{pre}}}}=[{\chi }^{{{\rm{pre}}}},{0}_{m-\tilde{m}}]$ and the vector ${\chi }^{{{\rm{pre}}}}$ of length $\tilde{m}$ contains the parameters for the terms ${\{{H}_{i}\}}_{i = 1}^{\tilde{m}}$ at the end of pre-training. More precisely, starting from${\rho }_{\chi }={e}^{\mathop{\sum }_{i = 1}^{\tilde{m}}{\chi }_{i}{H}_{i}}/Z$ and minimizingS(η∥ρ_χ) with respect toχ ensures Eq. (14) for any $S(\eta \!\!\parallel \!\!{\rho }_{{\chi }^{{{\rm{pre}}}}})\le S(\eta \!\!\parallel \!\!{\rho }_{{\chi }^{0}})$.

We refer to Supplementary Note 4 for the proof of this theorem. It applies to any method that is able to minimize the relative entropy with respect to a subset of the parameters. Crucially, all the other parameters are fixed to zero, and the pre-training needs to start from the maximally mixed state ${\mathbb{I}}/{2}^{n}$. Note that the maximally mixed state is not the most ‘distant’ state from the target state, and there exist states for which $S(\eta \!\!\parallel \!\!{\rho }_{\theta }) > S(\eta \!\!\parallel \!\!{\mathbb{I}}/{2}^{n})$. As an example of pre-training, one could use SGD as described above, and apply updates only to the chosen subset of parameters. With a suitable learning rate, this ensures that pre-training lowers the relative entropy compared to the maximally mixed state $S(\eta \!\!\parallel \!\!{\mathbb{I}}/{2}^{n})$. As a consequence, one can always add additional linearly independent terms to the QBM ansatz without having to retrain the model from scratch. The performance is guaranteed to improve, specifically toward the global optimum, due to the strict convexity of the relative entropy. By Eq. (14) and Pinsker’s inequality, the trace-distance to all the other observables reduces as well. This is in contrast to other QML models, which do not have a convex loss function. It is particularly useful if one can pre-train a certain subset classically before training the full model on a quantum device. For instance, in Supplementary Note 4, we present mean-field and Gaussian Fermionic pre-training strategies with closed-form expressions for the optimal subset of parameters.

Numerical experiments

To verify our theoretical findings, we perform numerical experiments of QBM learning on data sets constructed from a quantum and a classical source. In particular, we use expectation values of the Gibbs state of a 1D quantum XXZ model in an external field^61,62 and expectation values of a classical salamander retina data set⁶³. How to obtain the target state expectation values for both cases is explained in Supplementary Note 5.

First we focus on reducing the initial relative entropy $S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{0}})$ by QBM pre-training, following Theorem 3. We consider mean-field (MF), Gaussian Fermionic (GF), and geometrically local (GL) models as the pre-training strategies. The Hamiltonian ansatz of the MF model consists of all possible one-qubit Pauli terms ${\{{H}_{i}\}}_{i = 1}^{3n}={\{{\sigma }_{i}^{x},{\sigma }_{i}^{y},{\sigma }_{i}^{z}\}}_{i = 1}^{n}$ in Eq. (2), hence it has 3n parameters. The Hamiltonian of the GF model is a quadratic form ${{{\mathcal{H}}}}_{\theta }^{{{\rm{GF}}}}={\sum }_{i,j}{\tilde{\theta }}_{ij}{\vec{C}}_{i}^{{\dagger} }{\vec{C}}_{j}$ of Fermionic creation and annihilation operators, where ${\tilde{\theta }}_{ij}$ is the 2n × 2n Hermitian parameter matrix, which has n² free parameters. Here ${\overrightarrow{C}}^{{\dagger} }=[{c}_{1}^{{\dagger} },\ldots ,{c}_{n}^{{\dagger} },{c}_{1},\ldots ,{c}_{n}]$ with the operators satisfying {c_i, c_j} = 0 and $\{{c}_{i}^{{\dagger} },{c}_{j}\}={\delta }_{ij}$, where {A, B} = AB + BA is the anti-commutator. The advantage of the MF and GF pre-training is that there exists a closed-form solution given target expectation values ${\langle {H}_{i}\rangle }_{\eta }$ (see Supplementary Note 4).

In contrast, the GL models are defined with a Hamiltonian ansatz

$${{{\mathcal{H}}}}_{\theta }^{{{\rm{GL}}}}=\mathop{\sum}_{k=x,y,z}\mathop{\sum}_{\langle i,j\rangle }{\lambda }_{ij}^{k}{\sigma }_{i}^{k}{\sigma }_{j}^{k}+\mathop{\sum }_{i}^{n}{\gamma }_{i}^{k}{\sigma }_{i}^{k},$$

(15)

for which, in general, the parameter vector $\vec{\theta }\equiv \{\lambda ,\sigma \}$ cannot be found analytically. Here the sum 〈i, j〉 imposes some constraints on the (geometric) locality of the model, i.e., summing over all possible nearest neighbors in some d-dimensional lattice. In particular, we choose one- and two-dimensional locality constraints suitable to the assumptions given in previous work^53,54. In these specific cases the relative entropy is strongly convex, thus pre-training has the improved performance guarantees from Theorem 2.

In Fig. 2a, we show the relative entropy $S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{{{\rm{pre}}}}})$ obtained after pre-training with these models for 8-qubit problems. For MF and GF, we use the closed-form solutions, and for GL, we use exact gradient descent with learning rate of $\gamma =1/\tilde{m}$. As a comparison, we also show the result obtained for the QBM without pre-training, i.e., for the maximally mixed state S(η∥ρ_θ=0). We observe that for both targets, all pre-training strategies are successful in obtaining a lower $S(\eta \!\! \parallel \!\!{\rho }_{{\theta }^{{{\rm{pre}}}}})$ compared to the maximally mixed state. For the GL 1D ansatz, the target quantum state is contained within the QBM model space, which means that the relative entropy is zero after pre-training. This shows that having knowledge about the target (e.g., the fact that it is one-dimensional) could help inform QBM ansatz design and significantly reduce the complexity of QBM learning. The GF model, which has completely different terms in the ansatz, manages to reduce $S(\eta \!\!\parallel \!\!{\rho }_{{\theta }^{{{\rm{pre}}}}})$ by a factor of  ≈5 for the quantum target and  ≈4 for the classical target. By the Jordan-Wigner transformation, we can express the target XXZ model in a Fermionic basis. In this representation, the target only has a small perturbation compared to the model space of the GF model. This could explain the good performance of pre-training with the GF model.

Next, we investigate the effect of using pre-trained models as starting point for QBM learning with exact gradient descent. We extend all pre-trained models with additional linearly independent terms in the ansatz

$${{{\mathcal{H}}}}_{\theta }=\mathop{\sum}_{k=x,y,z}\mathop{\sum}_{i,j > i}{\lambda }_{ij}^{k}{\sigma }_{i}^{k}{\sigma }_{j}^{k}+\mathop{\sum }_{i}^{n}{\gamma }_{i}^{k}{\sigma }_{i}^{k},$$

(16)

where now, compared to Eq. (15), any qubit can be connected to any other qubit, and we do not have a constraint on the geometric locality. This is the fully connected QBM Hamiltonian used in previous work^18,43. We now consider data from the quantum target $\eta ={e}^{{{{\mathcal{H}}}}_{{{\rm{XXZ}}}}}/Z$ for 8 qubits.

In Fig. 2b, we show the quantum relative entropy during training when starting from different pre-trained models ${\rho }_{{\theta }^{0}}:={\rho }_{{\theta }^{{{\rm{pre}}}}}$. The initial parameter vector θ⁰ is the one obtained at the end of pre-training on quantum data in panel (a). We do not include gradient noise in this simulation, i.e., κ = ξ = 0, and we use a learning rate of γ = 1/(2m). The performance of the MF pre-trained model (orange line) is better than that of the vanilla model (blue line) for all t. However, the improvement is modest. Starting from a GL 2D model (red line) has a much more significant effect, with $S(\eta \!\!\parallel \!\! {\rho }_{{\theta }^{t}})$ being an order of magnitude smaller than that of the vanilla model at all iterations t. This pre-training strategy requires very few gradient descent iterations (dark gray area). This could be stemming from the strong convexity of this particular pre-training model. In general, the benefits of pre-training need to be assessed on a case-by-case basis, as the size of the improvement depends on the particular target and the particular pre-training model used. Importantly, we only proved Theorem 1 for a learning rate of $\gamma =\min \left\{\frac{1}{L},\frac{\epsilon }{4{m}^{2}({\kappa }^{2}+{\xi }^{2})}\right\}$. Therefore, choosing a larger learning rate might reduce the benefits of pre-training.

Lastly, we numerically confirm our bound on the number of SGD iterations (Eq. (8) in Theorem 1). We consider data from the classical salamander retina target with 8 features and a fully connected QBM model on 8 qubits. In Fig. 3, we compare training with two different noise strengths κ² + ξ². We implemented these settings by adding Gaussian noise, effectively simulating the noise strength determined by the number of data points in the data set and the number of measurements of the Gibbs state on a quantum device. Using the standard Monte Carlo estimate, at each update iteration, we require a mini-batch of data samples of size $\,\frac{1}{{\xi }^{2}}$, and a number of measurements $\frac{1}{{\kappa }^{2}}$ (assuming these measurements can be performed without additional hardware noise). We could even use mini batches of size 1 and a single measurement, as long as the expectation values are unbiased. For both noise strengths, we obtain the desired target precision of ϵ = 0.1 within 40000 iterations. This is well within the bound of order 10⁹ on the number of iterations obtained from Theorem 1, which is the worst-case scenario. For the interested reader, in Supplementary Note 3, we provide additional numerical evidence confirming the scaling behavior of our theorems.

Fig. 3: The maximum error in the expectation values versus the number of iterations of stochastic gradient descent (SGD).

The target η is made of 8 features from the classical salamander retina data set, the model ${\rho }_{{\theta }^{t}}$ is a quantum Boltzmann machine (QBM). When computing expectation values for the gradient, we allow precision ξ for the target and precision κ for the QBM. We compare the combined noise strength of 0.01 (blue line) to 0.05 (orange line). We aim for a maximum error of ϵ = 0.1 (red dashed line) and use a learning rate of $\gamma =\frac{\epsilon }{4{m}^{2}({\kappa }^{2}+{\xi }^{2})}$. SGD converges within a number of iterations consistent with Theorem 1.

Generalization

Before concluding our work, in this section, we briefly comment on the generalization capability of the fully connected QBM to which our convergence results apply. In particular, we connect with a result proved by Aaronson⁶⁴, which concerns the learnability of quantum states.

Theorem 4 (Theorem 1.1 in ref. ⁶⁴)

Let η be a 2ⁿ-dimensional mixed state, and let ${{\mathcal{D}}}$ be any probability measure over two-outcome measurements. Then given samples E₁, …, E_m drawn independently from ${{\mathcal{D}}}$, with probability at least 1 − ν, the samples have the following generalization property: any hypothesis stateρ such that $| {\langle {E}_{i}\rangle }_{\rho }-{\langle {E}_{i}\rangle }_{\eta }| \le \zeta \varepsilon$ for all i ∈ {1, …, m} will also satisfy

$${\Pr }_{E \sim {{\mathcal{D}}}}\left(| {\langle E\rangle }_{\rho }-{\langle E\rangle }_{\eta }| \le \varepsilon \right)\ge 1-\zeta ,$$

(17)

provided we took

$$m\ge \frac{C}{{\zeta }^{2}{\varepsilon }^{2}}\left(\frac{n}{{\zeta }^{2}{\varepsilon }^{2}}{\log }^{2}\frac{1}{\zeta \varepsilon }+\log \frac{1}{\nu }\right)$$

(18)

for some large enough constant C.

In other words, when a hypothesis state ρ matches the expectation values of m randomly sampled measurement operators from distribution ${{\mathcal{D}}}$, then, with high probability, most expectation values of the other measurement operators from ${{\mathcal{D}}}$ match up to error ε. Comparing to Definition 1, we can identify the learned QBM ρ_θ as a specific hypothesis state that matches the expectation values of operators ${\{{H}_{i}\}}_{i = 1}^{m}$ of the target η. Our convergence results show how many Gibbs state samples are required to obtain such a hypothesis state. Thus, our QBM learning result in Theorem 1, in a sense, complements Theorem 4 and provides a concrete algorithm for finding the hypothesis ρ with ${{\mathcal{O}}}({{\rm{poly}}}(n))$ samples. One distinction is that in QBM learning, we already assume access to a fixed set of measurement operators which defines the Hamiltonian ansatz, instead of randomly sampling operators from a distribution.

In order to say something about generalization, we now consider a scenario in which the user is interested in solving the QBM learning problem for some fixed (potentially exponentially large) number of two-outcome measurement operators ${\{{H}_{i}\}}_{i = 1}^{K}$. Then by defining ${{\mathcal{D}}}$ as the uniform distribution over the set ${\{{H}_{i}\}}_{i = 1}^{K}$, and constructing the QBM ansatz by sampling m < K operators from ${{\mathcal{D}}}$, we can directly apply Theorem 4 for generalization. In particular, defining the ansatz in this way ensures that our trained QBM will, with high probability, generalize to any other observable sampled from ${{\mathcal{D}}}$, including ones that are not in the ansatz.

Conclusions

In this paper, we give an operational definition of quantum Boltzmann machine (QBM) learning. We show that this problem can be solved with polynomially many preparations of quantum Gibbs states. To prove our bounds, we use the properties of the quantum relative entropy in combination with the performance guarantees of stochastic gradient descent (SGD). We do not make any assumption on the form of the Hamiltonian ansatz, other than that it consists of polynomially many terms. This is in contrast with earlier works that looked at the related Hamiltonian learning problem for geometrically local models^53,54. There, strong convexity is required in order to relate the optimal Hamiltonian parameters to the Gibbs state expectation values. In our machine learning setting, we do not know the form of the target Hamiltonian a priori. Therefore, we argue that learning the exact parameters is irrelevant, and one should focus directly on the expectation values. Our bounds only require L-smoothness of the relative entropy and apply to all types of QBMs without hidden units.

We also show that our theoretical sampling bounds can be tightened by lowering the initial relative entropy of the learning process. We prove that pre-training on any subset of the parameters is guaranteed to perform better than (or equal to) the maximally mixed state. This is beneficial if one can efficiently perform the pre-training, which we show is possible for mean-field, Gaussian Fermionic, and geometrically local QBMs. We verify the performance of these models and our theoretical bounds with classical numerical simulations. From this, we learn that knowledge about the target (e.g., its dimension, degrees of freedom, etc.) can significantly improve the training process. Furthermore, we find that our generic bounds are quite loose, and in practice, one could get away with a much smaller number of samples.

This brings us to interesting avenues for future work. One possibility consists of tightening the sample bound by going beyond the plain SGD method that we have used here. This could be done by adding momentum, by using other advanced update schemes^28,65, or by exploiting the convexity of the relative entropy. While we believe this can improve the ${{\mathcal{O}}}({{\rm{poly}}}(m,\frac{1}{\epsilon }))$ scaling in our bounds, we note that it does not change the main conclusion of our paper: the QBM learning problem can be solved with polynomially many preparations of Gibbs states. Another important direction is the investigation of different ansätze and their performance. Generative models are often assessed in terms of training quality⁶⁶, but generalization capabilities have been recently investigated by both classical^47,67 and quantum^68,69 machine learning researchers. For the case of QBMs, we employ an alternative definition of generalization⁶⁴ and show how it can be used to construct ansätze. The numerical investigation of this method is an interesting venue for future work.

Our pre-training result could be useful for implementing QBM learning on near-term and early fault-tolerant quantum devices. To this end, one would use a quantum computer as a Gibbs sampler. There exists a plethora of quantum algorithms (e.g., see refs. ^{36,38,40,41,42}) that prepare Gibbs states with a quadratic improvement in time complexity over the best existing classical algorithms. Moreover, the use of a quantum device gives an exponential reduction in space complexity in general. One can also sidestep the Gibbs state preparation and use algorithms that directly estimate Gibbs state expectation values, e.g., by constructing classical shadows of pure thermal quantum states⁴³. This reduces the number of qubits and, potentially, the circuit depth.

Finally, our results open the door to novel methods for the incremental learning of QBMs driven by the availability of both training data and quantum hardware. For example, one could select a Hamiltonian ansatz that is very well suited for a particular quantum device. After exhausting all available classical resources during the pre-training, one enlarges the model and continues the training on the quantum device, which is guaranteed to improve the performance. As the quantum hardware matures, it allows us to execute deeper circuits and to further increase the model size. Incremental QBM training strategies could be designed to follow the quantum hardware roadmap, toward training ever larger and more expressive quantum machine learning models.