Abstract
Mechanical bound states in the continuum (BICs) present an alternative avenue for developing high-frequency, high-Q mechanical resonators, distinct from the conventional band structure engineering method. While symmetry-protected mechanical BICs have been realized in phononic crystals, the observation of accidental mechanical BICs—whose existence is independent of mode symmetry and tunable by structural parameters—has remained elusive. This challenge is primarily attributed to the additional radiation channel introduced by the longitudinal component of elastic waves. Here, we employ a coupled wave theory to predict and experimentally demonstrate mechanical accidental BICs within a high-aspect-ratio gallium arsenide phononic crystal grating. We observe the merging process of accidental BICs with symmetry-protected BICs, resulting in reduced acoustic radiation losses compared to isolated BICs. This finding opens up new possibilities for phonon trapping using BIC-based systems, with potential applications in sensing, transduction, and quantum measurements.
Similar content being viewed by others
Introduction
Bound states in the continuum (BICs) constitute a unique category of states existing within the continuum spectrum of open systems, yet effectively decoupled from radiating waves that could dissipate energy. BICs have been extensively studied across various physical domains, including optics1,2,3, acoustics4,5,6, and mechanics7,8. The distinctive features of BIC modes, including high-quality factors and substantial mode sizes, have found applications in low-threshold lasing9,10,11, ultrasensitive sensing12,13,14, and efficient harmonic generation15,16,17. The introduction of the BIC concept to mechanical systems has opened a new avenue for the creation of high-quality factor, high-frequency mechanical resonators, departing from the conventional waveguide modes18 and band-engineered modes below the sound cone19,20. Mechanical BICs can be realized due to symmetry mismatch between the mechanical mode and the outgoing radiation field7,21—termed symmetry-protected BICs—and destructive interference between two coexisting modes8, known as Friedrich-Wintgen BICs. Compared to released mechanical micro-resonators, BIC-based mechanical systems offer advantages such as enhanced thermal capacity and macroscopic mode sizes. These characteristics hold potential for mitigating thermal noises in quantum measurements22,23,24,25 and enabling high-throughput sensing26,27,28.
However, a crucial breed of BICs, referred to as accidental BICs, has yet to be realized in mechanical systems. Distinct to the symmetry-protected BIC and Friedrich-Wintgen BIC, which have been employed in various platforms, including optomechanical crystals21 and microresonators8, accidental BICs do not require radiation-forbidden symmetries or depend on the interference of two coupled modes. Instead, they emerge “accidentally” under specific system parameters that permit zero-radiation solutions1. Achieving accidental BICs in mechanical systems poses a substantial challenge, primarily due to an additional loss channel introduced by the longitudinal component of elastic waves7,29, in contrast to electromagnetic waves. For a mechanical resonance to manifest as an accidental BIC, it must simultaneously decouple from both transverse and longitudinal radiative waves. Because of the distinct mechanism, accidental BICs can exist in proximity to symmetry-protected BICs by tuning system parameters, resulting in suppressed radiation loss for all surrounding modes. This merging-BIC mechanism has been shown to effectively mitigate radiation losses in structures affected by disorder-induced intermodal scattering3,11,30,31.
Here we employ a coupled wave theory to predict and experimentally realize mechanical accidental BICs within high-aspect-ratio gallium arsenide (GaAs) phononic crystal gratings. The mechanical accidental BIC can merge with the symmetry-protected BIC in the same acoustic band through single-parameter tuning. We experimentally observe enhanced quality factors of band-edge resonances of the phononic crystal grating as a direct evidence of the existence of accidental BICs and the merging BIC process3,9,11. The demonstrated Love-wave merging BICs hold great promise for various applications. Particularly, Love waves offer advantages over Rayleigh waves in sensing as they effectively decouple from compressional waves in liquids32,33,34. The BIC structure eliminates the need for multi-layered materials and complicated fabrication processes, potentially offering an improved method for utilizing Love waves in sensing applications. Moreover, the BIC phononic crystal gratings, featuring a large mode volume and a high fQ–product, provide a promising platform for exploring macroscopic quantum mechanical oscillators35,36,37.
Results and discussion
Phononic crystal gratings with accidental mechanical BICs
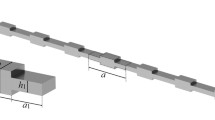
The GaAs phononic crystal grating with a double-slot unit cell is illustrated in Fig. 1a. For a one-dimensional phononic crystal grating aligned with the crystal axis of GaAs, the mechanical modes propagating along the x direction can be divided into two categories: Love-wave modes and Rayleigh-wave modes. By definition, the Love-wave mode is xz-plane-odd, and thus it only has y-displacement, because x- and z-displacements are uniform and thus even with respect to the xz-plane for a structure that is infinite along the y-direction. Similarly, the Rayleigh-wave mode is xz-plane-even, and thus it only has coupled x- and z-displacements (see Supplementary Note 1). For the Rayleigh-wave mode, regardless of its symmetry with respect to the yz-plane, it couples with radiation fields, because the x-polarized plane wave is odd and the z-polarized plane wave is even with respect to the yz-plane. For the Love-wave mode, which only has the y-displacement, it decouples from the radiation field if it is odd with respect to the yz-plane, because the y-polarized plane wave is even. Based on the symmetry analysis, the 1D mechanical grating only supports symmetry-protected BICs that are odd Love-wave modes. Table 1 lists common piezoelectric materials and their compatibility with symmetry-protected BICs in 1D phononic crystal gratings. We choose GaAs because it also has a shear piezoelectric component for excitation of the Love-wave modes.
a An illustration of the GaAs phononic crystal grating and the unit cell with the lattice constant a, the slot width g, the slot depth t and the pillar width w. b Mechanical band structure near the Γ point for the unit cell dimensions indicated in the text. L0 (L1) and R0 indicate the fundamental (second) Love-wave band and the fundamental Rayleigh-wave band, respectively. Stars indicate the symmetry-protected BIC at the Γ point and the accidental BIC along Γ − X. c Side and top view of the mode profile of the symmetry-protected BIC (left) and the accidental BIC (right).
We develop a coupled wave theory3,38,39 for elastic waves to identify mechanical grating structures with accidental BICs around the Γ point (Supplementary Note 2). The displacement field of the Bloch mode of the phononic crystal grating can be expanded using the basis of quasi-plane waves, \({{{{{{{{\bf{Q}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\parallel },z)={\sum}_{{{{{{{{\bf{G}}}}}}}}}{{{{{{{{\bf{Q}}}}}}}}}^{{{{{{{{\bf{G}}}}}}}}}(z)\exp \left[-i({{{{{{{\bf{k}}}}}}}}+{{{{{{{\bf{G}}}}}}}})\cdot {{{{{{{{\bf{r}}}}}}}}}_{\parallel }\right]\), where k is the Bloch wavevector, r∥ is the in-plane spatial vector, G = 2πmex/a (m ∈ Z) is the reciprocal vector and QG(z) is the corresponding Fourier component. For BIC modes near the Γ point, including both symmetry-protected and accidental ones, since they reside above the sound cone but below the diffraction limit (also called the folded sound cone), they are actually modes in the vicinity of the 2nd Γ point \((\pm \frac{2\pi }{a},0)\) before being folded to the Γ point (0, 0). For modes in the vicinity of the 2nd Γ point, Q±2π/a(z) are the dominant quasi-plane-wave components and Q0(z) is the only radiating component3,38,39,40. As a result, BIC modes satisfy Q0(z) = 0.
The radiation amplitude Q0(z) of the Love-wave mode at the 2nd Γ point can be perturbatively calculated using Q±2π/a(z):
where ρG and \({C}_{44}^{{{{{{{{\bf{G}}}}}}}}}\) are the Fourier components of the density and elastic tensor component C44 of the GaAs grating layer, ω is the frequency of the Bloch mode, \({{{{{{{\mathcal{G}}}}}}}}={[-{\omega }^{2}{\rho }^{0}-{\partial }_{z}({C}_{44}^{0}{\partial }_{z})]}^{-1}\) is the Green’s function corresponding to the elastic eigenmode equation, and the integral is performed in the grating layer (Supplementary Note 2). Symmetry-protected BIC is realized for QG(z) = −Q−G(z), which leads to cancellation of the two integrals corresponding to G = (±2π/a, 0) in Eq. (1) and thus a vanishing radiation amplitude Q0(z). On the other hand, if individual integral for \({{{{{{{\bf{G}}}}}}}}=(\pm \frac{2\pi }{a},0)\) of Eq. (1) is zero, an accidental BIC at the Γ point is realized. The structure parameters obtained from the coupled-wave theory then can be used to guide the ab initio simulation to identify structures with accidental BICs around the Γ point (Supplementary Note 2).
Based on the coupled wave theory and finite-element simulations (COMSOL), we designed GaAs phononic crystal gratings with Love-wave symmetry-protected BICs at the Γ point and accidental BICs on the same band by tuning the structural parameters. Figure 1b shows the mechanical band structure of the grating with a lattice constant a = 1198 nm, slot width g = 100 nm, slot depth t = 1000 nm and center pillar width w = 120 nm. The lowest Love-wave band (L0) supports a symmetry-protected BIC at the Γ point and accidental BICs along the Γ − X line at kx = ±0.18π/a. The mode profiles of the BICs are shown in Fig. 1c. The position of the accidental BICs can be tuned to move along the kx axis and merge with the symmetry-protected BICs at the Γ point.
Merging mechanical BICs
The k-position of the accidental BICs can be tuned by varying the grating parameters. For example, by reducing the lattice constant from 1198 to 1193 nm, the two accidental BICs shift toward the Γ point and eventually merge with the symmetry-protected BIC, forming a merged BIC (Fig. 2a, b). When the lattice constant is below 1193 nm, the grating structure only has one symmetry-protected BIC at the Γ point (Fig. 2c, a = 1165 nm). Such a merging behavior of the mechanical BICs is also illustrated by their topological charges. Because BICs have vanishing radiation amplitudes, the far-field polarization of BICs cannot be defined, which leads to singularity points in the far-field polarization map of Bloch modes (see Fig. 2a–c bottom panel) (“Methods”). These singularity points are characterized by a topological charge, i.e., the winding number of the polarization surrounding them7,40. During the merging process, the total topological charge is conserved40. Figure 2a–c shows the x- and y-components of the far-field polarization of Bloch modes of the L0 band and the topological charges of mechanical BICs before, at, and after BIC merging. On the other hand, due to the odd symmetry of the Love-wave mode, the z-component of the far-field polarization vanishes for Love-wave Bloch modes on the high-symmetric kx and ky axes, which are represented by nodal lines in the polarization map.
Numerically simulated Q of the mechanical Bloch mode (colormaps) and far-field polarization map (blue, yellow and red streamlines) corresponding to before merging (a, a = 1198 nm), at merging (b, a = 1193 nm), and after merging (c, a = 1165 nm). The topological charge of the mechanical BICs is indicated. Simulated Q corresponding to ky = 0 (d) and ky = π/400 μm−1 (e) before (blue), at (yellow), and after (red) BIC merging. f Simulated Q versus lattice constant for the grating length L = 400 μm (solid lines) and L = 120 μm (dashed lines) and different momentum kx = 0.09π/a (green), kx = 0.15π/a (purple), and kx = 0.2π/a (gray). g Simulated Q of 1 × 4 supercells with σ = 1% random variations of the slot width for lattice constant a = 1193 nm (yellow), 1185 nm (blue), and 1165 nm (red). ky = π/400 μm−1.
The merging of BICs enhances the quality factor (Q) of the Bloch modes in the vicinity of the BICs3,31,40. For an isolated BIC, the scaling of Q versus kx along the Γ − X line is given by \(Q\propto 1/{k}_{x}^{2}\) for kx ≪ π/a (Fig. 2d red line)3 (Supplementary Note 3). In the presence of two accidental BICs adjacent to the symmetry-protected BIC, the Q scaling becomes \(Q\propto 1/[{k}_{x}^{2}{({k}_{x}-{k}_{{{{{{{{\rm{BIC}}}}}}}}})}^{2}{({k}_{x}+{k}_{{{{{{{{\rm{BIC}}}}}}}}})}^{2}]\) (Fig. 2d blue line), where ±kBIC are the momenta of the accidental BICs (Supplementary Note 3). At the merging point, i.e., kBIC = 0, the merging BIC possesses \(Q\propto 1/{k}_{x}^{6}\), leading to enhanced quality factor for the Bloch modes near the merging BIC (Fig. 2d yellow line). Such Q-enhancement effect due to the merging BIC is also manifested at finite ky ≪ π/a (see derivation in Supplementary Note 3). This is verified by numerical simulations shown in Fig. 2e with the simulated Q(kx) for ky = π/400 μm−1 and a = 1198, 1193, 1165 nm. This result proves that the effect of merging BIC can persist in finite grating structures corresponding to small ky.
The standing-wave resonance of order {m, n} in finite grating structures is characterized by quantized momentum (kx, ky) = (mπ/Na, nπ/L), where N is the number of grating periods and L is the length of the grating along the y direction. To illustrate the effect of merging BIC on the Q of standing-wave resonances, we simulate the Q of Bloch modes of finite (kx, ky) for varying lattice constant across the merging point. In Fig. 2f, solid (dashed) lines represent the Q of Bloch modes with ky corresponding to n = 1 and L = 400 μm (L = 120 μm). For each ky, three different kx are simulated, kx = 0.09 π/a, 0.15 π/a, and 0.2 π/a, corresponding to green, purple, and gray lines. We find a peaked Q exists for all these cases as a result of merging BICs. The value of the peaked Q becomes larger for smaller kx, corresponding to a larger number of grating periods, and smaller ky, corresponding to longer gratings, as the Bloch mode approaches the merging BIC.
The enhanced quality factor due to the merging BIC is also manifested in grating structures with disorders3,41. This is because the merging BIC enhances the quality factor of all adjacent Bloch modes as shown in Fig. 2d, e, thus suppressing the radiation loss due to the disorder-induced intermodal scattering3,41. To show this, we simulate a super-cell structure with 4 unit cells and each unit cell has a random variation of the slot width (standard deviation ≈ 1%). As shown in Fig. 2g, for the same disorder level, the Q of the grating with the merging BIC (a = 1193 nm) is higher than that of the grating with isolated BICs (a = 1165 nm). Such protection against disorders remains effective for a wide range of kx and lattice constants near the merging-BIC design, which reveals the robustness of the merging-BIC mechanism. Since disorders are inevitable in fabricated structures, the merging BIC mechanism is expected to mitigate scattering losses compared to structures with only isolated BICs.
Experimental demonstrations
To experimentally demonstrate the accidental mechanical BIC and the BIC merging process, we fabricated GaAs phononic crystal gratings (Fig. 3a, b; see “Methods” for device fabrication). We also fabricated interdigital transducers (IDTs) for piezoelectric excitation and probe of surface acoustic waves coupled with the phononic crystal grating (Fig. 3c). A vector network analyzer (VNA) is used to measure the power transmission spectrum ∣S21∣2 and reflection spectrum ∣S11∣2 of the device (“Methods). For the IDT with a pitch about 1600 nm, a Love-wave mode with the frequency f0 around 2 GHz can be excited (see Fig. 3d inset). A typical IDT transmission spectrum ∣S21∣2 through the bulk GaAs without the phononic crystal grating is shown in Fig. 3d (blue curve), where the number of IDT finger pairs is B = 50, resulting in a bandwidth of about 60 MHz. The fringes are caused by the electromagnetic interference between the two probes and can be subtracted using the time-gating method (see Supplementary Note 4 for time-gated spectrum of IDTs). The electromagnetic-interference subtracted spectrum matches the theoretical modeling given by \(A({f}_{0},\eta ){B}^{2}{\left(\sin (B(f-{f}_{0})/{f}_{0})/(B(f-{f}_{0})/{f}_{0})\right)}^{2}\), where the amplitude A(f0, η) is determined by the piezoelectricity of the material and the duty cycle η of the IDT42. We then used such IDTs to probe phononic crystal gratings. The higher-frequency Love-wave bands of the grating correspond to higher-order modes along the z direction, which is mode-mismatch with the fundamental Love-wave mode of the IDT. Consequently, the IDT transmission is significantly attenuated if the IDT frequency is higher than the L0 band (along kx) of the grating and coincides with the effective bandgap of the phononic crystal grating near the Γ point (Fig. 3e). In contrast, when the IDT frequency lies within the L0 band (along kx) of the grating, the resonance-assisted transmission occurs (Fig. 3f). In this case, multiple discrete peaks are observed, corresponding to the standing-wave resonances of the phononic crystal grating with wavevector kx = mπ/Na (see Supplementary Note 5 and 6 for the modeling and simulated transmission spectrum). The free spectral range of these standing-wave resonances is determined by the phononic crystal band and is distinct from the electromagnetic interference-induced fringes of the bare IDT spectrum shown in Fig. 3d. The fringe of the phononic crystal grating remains the same after the time-gating processing of the transmission spectrum (see Supplementary Note 4 for time-gated transmission spectrum of the grating).
a, b Scanning electron microscopy images of the GaAs phononic crystal grating. c Optical microscopy image of the interdigital transducers (IDTs) and a grating with 200 periods. The microwave transmission (blue) and reflection (red) spectrum of bulk GaAs (d), a grating with the L0 band mismatched with the IDT frequency (e), and a grating with the L0 band matched with the IDT frequency (f). The IDT Love-wave mode profile is shown in the inset of (d).
We fabricated three sets of phononic crystal gratings with different number of grating periods N and grating length L: (N = 50, L = 120 μm), (N = 100, L = 120 μm), and (N = 200, L = 400 μm). In each set, the lattice constant is scanned in a range of 60 nm around a = 1193 nm, corresponding to the merging BIC design, with a step size of 2 nm. We measured the microwave transmission of each device at room temperature and inferred the Q of the standing-wave resonances of the grating by fitting the transmission spectrum (Supplementary Note 5). The Q of the observed lowest-order standing-wave resonance in each device is summarized in Fig. 4a–c for the three sets of gratings. Within each set of gratings, the measured Q shows a trend that increases with the lattice constant, peaks at a lattice constant around a = 1193 nm, and then decreases with the lattice constant, which is consistent with the simulation (Fig. 2f). This is a direct observation of the accidental BIC and its merging with the symmetry-protected BIC3,9,11. The fluctuation of Qs is due to the fact that each grating has different fabrication induced imperfections. Comparing different sizes of gratings, the (N = 200, L = 400 μm) set has the highest Q at the merging point, because its standing-wave resonances have the smallest ky. Since the fabrication-imperfection-induced scattering loss is the dominant loss mechanism, the measured Q of the BIC grating is lower than the theoretical prediction based on simulations of a few unit cells10,11,30. The high-aspect ratio, high GHz frequency (and thus short wavelength), and the lossy continuum also make the BIC phononic crystal grating more prone to scattering losses, as compared with other unreleased mechanical resonators using modes under the sound cone8,18,19,20.
a–c Measured Q of the observed lowest-order standing-wave resonance in the three sets of gratings with varying lattice constants. a (N = 50, L = 120 μm), b (N = 100, L = 120 μm), c (N = 200, L = 400 μm). The shaded areas are used to show the trend of Qs. d–f Microwave transmission spectrum of the gratings with the highest Q in the three sets. The zoom-in plots show a narrower frequency range. Background-subtracted, fitted resonances are also shown with the amplitude measured by the linear scale on the right axis.
Figure 4d–f shows the transmission spectrum of the gratings with the highest Q in the three sets. The measured transmission spectrum can be fit using a coupled mode theory (Supplementary Note 5). For the transmission coefficient at the resonance frequency, \(| {S}_{12}{| }^{2}\propto {(\frac{{\kappa }_{e}}{\kappa })}^{2}\), where κ ≡ ω/Q is the total dissipation rate of the standing-wave resonance and κe is the coupling rate with the IDT-excited surface acoustic wave. As a result, given the similar noise floor in the transmission spectrum and signal-to-noise ratio, the lowest-order resonances observed in the three sets of gratings have a comparable κe/κ ratio. We examine three gratings, with one from each set, that are furthest away from the merging BIC point. The Q of the lowest-order resonance of these three gratings have a ratio about QN = 50 : QN = 100 : QN = 200 ≈ 1 : 2 : 4, (i.e., QN = 50 = 235, QN = 100 = 397, QN = 200 = 805), and thus we infer Qe,N = 50 : Qe,N = 100 : Qe,N = 200 ≈ 1 : 2 : 4 (Qe ≡ ω/κe). Our analysis shows that this can only be satisfied when the observed lowest-order resonances of the three sets of gratings have a similar kx(=mπ/Na), which is found to be in the range of (0.04π/a, 0.08π/a) (see Supplementary Note 7 and 8). The kx value of the observed lowest-order resonances is sufficiently close to the Γ point, resulting in the enhanced Q of these resonances due to the merging BIC effect. The lower Q observed for the N = 50 set compared to the N = 100 set is due to the fact the resonance of a smaller grating has a broader momentum distribution than the resonance of a larger grating with the same kx (Supplementary Note 8), leading to more radiation losses.
In conclusion, we have realized mechanical accidental BICs and their merging with symmetry-protected BICs in GaAs phononic crystal gratings. The merging BIC is experimentally verified via the observation of suppressed acoustic radiation loss of band-edge resonances as compared with the case of isolated BICs. The measured quality factor of the merging mechanical BIC in this study is still limited by scattering losses due to the high-aspect-ratio grating (see Supplementary Note 9 and 10), which is sensitive to fabrication imperfections. The scattering loss can be mitigated by adopting a material structure with acoustic impedance-mismatched device layer and substrate and improving fabrication precision. The acoustic coupled wave theory developed here can be used to explore accidental BICs and BIC merging in other mechanical systems beyond 1D gratings. The observation of mechanical merging BIC enables an alternative approach for creating mechanical oscillators with high frequencies and macroscopic sizes, which hold great promises in various applications from signal transduction to sensing.
Methods
Far-field polarization calculation
The displacement field of the phononic crystal grating can be expressed as \({{{{{{{\bf{Q}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\parallel },z)={\sum }_{{{{{{{{\bf{G}}}}}}}}}{{{{{{{{\bf{Q}}}}}}}}}_{{{{{{{{\bf{G}}}}}}}}}(z){e}^{i({{{{{{{\bf{G}}}}}}}}+{{{{{{{{\bf{k}}}}}}}}}_{\parallel })\cdot {{{{{{{{\bf{r}}}}}}}}}_{\parallel }}\), where r∥ and k∥ are the in-plane coordinate and wavevector, and G is the reciprocal lattice vector. The far-field radiation amplitude c is given by the zeroth-order component \({{{{{{{\bf{c}}}}}}}}\equiv {{{{{{{{\bf{Q}}}}}}}}}_{0}={\int}_{{{{{{{{\rm{u.c.}}}}}}}}}{{{{{{{\bf{Q}}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\parallel },{z}_{0}){e}^{-i{{{{{{{{\bf{k}}}}}}}}}_{\parallel }\cdot {{{{{{{{\bf{r}}}}}}}}}_{\parallel }}d{{{{{{{{\bf{r}}}}}}}}}_{\parallel }\), where the integral is performed in the horizontal plane at z = z0 in the unit cell area. The far-field polarization then is defined as the long-axis A of the polarization ellipse7,43:
Device fabrication
The devices are fabricated on a GaAs wafer with [100] orientation. A 140 nm thick SiO2 is deposited as the hard mask. The phononic crystal gratings are patterned by electron beam lithography using ZEP 520A as the mask. The pattern is transferred to the hard mask by inductively coupled plasma reactive ion etch (ICP-RIE) of SiO2 using SF6 and CHF3, and subsequently transferred to GaAs with another ICP-RIE using BCl3, Ar and N2. The IDTs are defined by a second electron beam lithography with PMMA as the mask, followed by electron beam evaporation of 10 nm chromium and 70 nm gold and subsequent lift-off process.
Measurement
The RF signal is generated by a vector network analyzer (ZVL13, Rohde & Schwarz) and transmitted via the device using impedance-matched RF probes (T26, MPI). The transmission and reflection spectrum of the device is then measured by the vector network analyzer.
Data availability
Data supporting the findings of this study are available within the article and its Supplementary Information, or from the corresponding author upon reasonable request.
References
Hsu, C. W. et al. Observation of trapped light within the radiation continuum. Nature 499, 188–191 (2013).
Plotnik, Y. et al. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 107, 183901 (2011).
Jin, J. et al. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering. Nature 574, 501–504 (2019).
Cumpsty, N. A. & Whitehead, D. The excitation of acoustic resonances by vortex shedding. J. Sound Vib. 18, 353–369 (1971).
Hein, S., Koch, W. & Nannen, L. Trapped modes and Fano resonances in two-dimensional acoustical duct–cavity systems. J. Fluid Mech. 692, 257–287 (2012).
Lyapina, A., Maksimov, D., Pilipchuk, A. & Sadreev, A. Bound states in the continuum in open acoustic resonators. J. Fluid Mech. 780, 370–387 (2015).
Tong, H., Liu, S., Zhao, M. & Fang, K. Observation of phonon trapping in the continuum with topological charges. Nat. Commun. 11, 5216 (2020).
Yu, Y., Xi, X. & Sun, X. Observation of mechanical bound states in the continuum in an optomechanical microresonator. Light Sci. Appl. 11, 328 (2022).
Kodigala, A. et al. Lasing action from photonic bound states in continuum. Nature 541, 196–199 (2017).
Ren, Y. et al. Low-threshold nanolasers based on miniaturized bound states in the continuum. Sci. Adv. 8, eade8817 (2022).
Hwang, M.-S. et al. Ultralow-threshold laser using super-bound states in the continuum. Nat. Commun. 12, 4135 (2021).
Yesilkoy, F. et al. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat. Photonics 13, 390–396 (2019).
Romano, S. et al. Label-free sensing of ultralow-weight molecules with all-dielectric metasurfaces supporting bound states in the continuum. Photonics Res. 6, 726–733 (2018).
Wang, Y., Han, Z., Du, Y. & Qin, J. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 10, 1295–1307 (2021).
Koshelev, K. et al. Nonlinear metasurfaces governed by bound states in the continuum. ACS Photonics 6, 1639–1644 (2019).
Carletti, L., Koshelev, K., De Angelis, C. & Kivshar, Y. Giant nonlinear response at the nanoscale driven by bound states in the continuum. Phys. Rev. Lett. 121, 033903 (2018).
Liu, Z. et al. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett. 123, 253901 (2019).
Xu, X.-B. et al. High-frequency traveling-wave phononic cavity with sub-micron wavelength. Appl. Phys. Lett. 120, 163503 (2022).
Shao, L. et al. Phononic band structure engineering for high-q gigahertz surface acoustic wave resonators on lithium niobate. Phys. Rev. Appl. 12, 014022 (2019).
Kolvik, J., Burger, P., Frey, J. & Van Laer, R. Clamped and sideband-resolved silicon optomechanical crystals. Optica 10, 913–916 (2023).
Liu, S., Tong, H. & Fang, K. Optomechanical crystal with bound states in the continuum. Nat. Commun. 13, 3187 (2022).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Palomaki, T., Teufel, J., Simmonds, R. & Lehnert, K. W. Entangling mechanical motion with microwave fields. Science 342, 710–713 (2013).
Riedinger, R. et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 530, 313–316 (2016).
Arrangoiz-Arriola, P. et al. Resolving the energy levels of a nanomechanical oscillator. Nature 571, 537–540 (2019).
Teufel, J. D., Donner, T., Castellanos-Beltran, M., Harlow, J. W. & Lehnert, K. W. Nanomechanical motion measured with an imprecision below that at the standard quantum limit. Nat. Nanotechnol. 4, 820–823 (2009).
Kolkowitz, S. et al. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603–1606 (2012).
Yue, M. et al. Label-free protein recognition two-dimensional array using nanomechanical sensors. Nano Lett. 8, 520–524 (2008).
Zhao, M. & Fang, K. Mechanical bound states in the continuum for macroscopic optomechanics. Opt. Express 27, 10138–10151 (2019).
Chen, Z. et al. Observation of miniaturized bound states in the continuum with ultra-high quality factors. Sci. Bull. 67, 359–366 (2022).
Kang, M. et al. Merging bound states in the continuum by harnessing higher-order topological charges. Light Sci. Appl. 11, 228 (2022).
Jakoby, B. & Vellekoop, M. J. Properties of Love waves: applications in sensors. Smart Mater. Struct. 6, 668 (1997).
Du, J., Harding, G., Ogilvy, J. A., Dencher, P. & Lake, M. A study of Love-wave acoustic sensors. Sens. Actuators A Phys. 56, 211–219 (1996).
Schlensog, M. D., Gronewold, T. M., Tewes, M., Famulok, M. & Quandt, E. A Love-wave biosensor using nucleic acids as ligands. Sens. Actuators B Chem. 101, 308–315 (2004).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391 (2014).
Gut, C. et al. Stationary optomechanical entanglement between a mechanical oscillator and its measurement apparatus. Phys. Rev. Res. 2, 033244 (2020).
Wilson, D. J. et al. Measurement-based control of a mechanical oscillator at its thermal decoherence rate. Nature 524, 325–329 (2015).
Liang, Y., Peng, C., Sakai, K., Iwahashi, S. & Noda, S. Three-dimensional coupled-wave model for square-lattice photonic crystal lasers with transverse electric polarization: a general approach. Phys. Rev. B 84, 195119 (2011).
Yang, Y., Peng, C., Liang, Y., Li, Z. & Noda, S. Analytical perspective for bound states in the continuum in photonic crystal slabs. Phys. Rev. Lett. 113, 037401 (2014).
Zhen, B., Hsu, C. W., Lu, L., Stone, A. D. & Soljačić, M. Topological nature of optical bound states in the continuum. Phys. Rev. Lett. 113, 257401 (2014).
Regan, E. C. et al. Direct imaging of isofrequency contours in photonic structures. Sci. Adv. 2, e1601591 (2016).
Datta, S. Surface Acoustic Wave Devices (Prentice-Hall, 1986).
Berry, M. Index formulae for singular lines of polarization. J. Opt. A Pure Appl. Opt. 6, 675 (2004).
Bright, V. & Hunt, W. Bleustein–Gulyaev waves in gallium arsenide and other piezoelectric cubic crystals. J. Appl. Phys. 66, 1556–1564 (1989).
Cheng, G. & Venkatesh, T. Nanoindentation response of anisotropic piezoelectric materials. Philos. Mag. Lett. 92, 278–287 (2012).
Acknowledgements
This work is supported by the U.S. National Science Foundation (Grant Nos. 1944728 and 2137642) and the Office of Naval Research (Grant No. N00014-21-1-2136).
Author information
Authors and Affiliations
Contributions
S.L. developed the coupled wave theory. S.L. and H.T. designed the device. H.T. manufactured the device. H.T. and S.L. performed the measurement and data analysis. S.L., H.T., and K.F. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tong, H., Liu, S. & Fang, K. Merging mechanical bound states in the continuum in high-aspect-ratio phononic crystal gratings. Commun Phys 7, 197 (2024). https://doi.org/10.1038/s42005-024-01692-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-024-01692-9
- Springer Nature Limited