Pseudospin-triplet pairing in iron-chalcogenide superconductors

Abstract

Understanding the pairing symmetry is a crucial theoretical aspect in the study of unconventional superconductivity for interpreting experimental results. Here we study superconductivity of electron systems with both spin and pseudospin-1/2 degrees of freedom. By solving linearized gap equations, we derive a weak coupling criterion for the even-parity spin-singlet pseudospin-triplet pairing. It can generally mix with the on-site s-wave pairing since both of them belong to the same symmetry representation (A_1g) and their mixture could naturally give rise to anisotropic intra-band pairing gap functions with or without nodes. This may directly explain why some of the iron-chalcogenide superconductors are fully gapped (e.g. FeSe thin film) and some have nodes (e.g. LaFePO and LiFeP). We also find that the anisotropy of gap functions can be enhanced when the principal rotation symmetry is spontaneously broken in the normal state such as nematicity, and the energetic stabilization of pseudospin-triplet pairings indicates the coexistence of nematicity and superconductivity. This could be potentially applied to bulk FeSe, where gap anisotropy has been experimentally observed.

Introduction

The symmetry principle is one of the most powerful tools to diagnose low-energy electronic band structures, lattice vibrations, and linear responses¹, and is also valuable to explore various symmetry-breaking ordered phases such as magnetism, charge/spin density-wave, nematicity and superconductivity². The crystal symmetry of a solid-state system dictates the normal band structures it hosts near the Fermi level, which could in turn determine the most favorable superconducting pairing symmetry^3,4. This symmetry principle for superconductors (SC) is recently extended to investigate multi-band unconventional superconductivity^5,6,7. Interestingly, the orbital-independent and orbital-dependent pairings that belong to the same symmetry representation may coexist with each other⁸. Such orbital-dependent pairings have been studied in a wide variety of systems with multi-band character, including Sr₂RuO₄⁹, iron-chalcogenide SCs^10,11,12,13, Cu-doped Bi₂Se₃¹⁴ and half-Heusler compounds^15,16,17,18, from which the guiding principle by symmetry is crucial to understanding the nature of unconventional superconductivity.

A few specific systems can be effectively characterized by a general normal-state model Hamiltonian that contains both spin ({↑, ↓}) and pseudospin ({1, 2}) degrees of freedom, where pseudospin could originate from two atomic orbitals, two sublattices, two layers, or two valleys⁶. We start from a spin-singlet centrosymmetric SC to explore the existence of even-parity pseudospin-triplet pairings, for example, c_1,↑(k)c_2,↓( − k) + c_2,↑(k)c_1,↓( − k) − c_1,↓(k)c_2,↑( − k) − c_2,↓(k)c_1,↑( − k), and further investigate their valuable roles in tailoring anisotropic pairing gap functions with or without nodes¹⁹. Different from spin-triplet pairings, spin-singlet pseudospin-triplet pairings have not been much explored in real materials since such pairings are usually considered to be energetically unfavorable. This is partly due to the common belief that the double degeneracy of the two orbitals is lifted by orbital hybridization so that the orbital-dependent pairing would be severely suppressed under crystal field splitting or electron-electron repulsive interaction. One aim of this work is concerned with the possible condition for the existence of even-parity spin-singlet orbital-dependent pairings, and possible applications to real materials.

On the other hand, the effects of symmetry breaking in unconventional SCs is an important topic that has attracted tremendous interest. The symmetry could be broken explicitly by external fields or strain, or be broken spontaneously from many-body interactions. Two typical examples are rotational symmetry breaking^20,21 and time-reversal-symmetry (TRS) breaking^{22,23,24,25,26}. Besides, the interplay between nematicity and superconductivity is yet to be fully understood in some real materials, such as FeSe^12,27, where gap functions can be highly anisotropic. These systems are all multi-band SCs, while symmetry-reducing signatures are experimentally observed above the superconducting transition temperature, which is mainly caused by both crystal field splittings and interaction-induced order parameters (e.g. nematicity). Thus, discovering the coexistence of nematicity and superconductivity in these multi-band systems can shed new light on understanding the underlying favorable pairing symmetries.

The main finding of this work is that the anisotropic gap functions with or without nodes could be attributed to the mixing of isotropic s-wave pairing and even-parity spin-singlet pseudospin-triplet pairing, even though both of them belong to the A_1g symmetry representation. For technical conveniences, we adopt an orbital d_o(k)-vector notations¹¹ to describe the pairing matrix and similarly a g_o(k)-vector for orbital hybridization in the two-orbital subspace ({1, 2}). Solving linearized gap equations, we show that the presence of g_o-vector generally suppresses the superconductivity with orbital d_o-vector except for d_o(k)∥g_o(k), which is consistent with the concept of superconducting fitness⁶. This sets up weak-coupling criteria for A_1g-type orbital-dependent pairings that could naturally give rise to anisotropic gap functions in real superconducting materials. Moreover, we reveal a deep connection between two-orbital nematic SC and pseudospin-triplet pairings. Within the mean-field theory for electron-electron repulsive interactions, the nematic order develops in the orbital subspace at T < T_nem, which also contributes to the total orbital hybridization, g_tot = g_o + g_nem. This leads to the stabilization of a nematic orbital d_o-vector for d_o(k)∥g_tot(k), indicating the coexistence of nematicity and superconductivity. The direct applications to FeSe^12,27 are also discussed. We also generalize it to a two-valley system with C₆ breaking terms (e.g., Kekulé distortion). In the end, we also predict an orbital-polarized superconducting state.

Results

Classification of Spin-singlet Orbital-triplet pairings

To explore the weak-coupling criterion for the energetically favorable even-parity spin-singlet pseudospin-triplet pairing, we consider the mean-field pairing Hamiltonian,

$${{{{{{\mathcal{H}}}}}}}_{\Delta }=\mathop{\sum}\limits_{{{{{{\bf{k}}}}}}}\mathop{\sum}\limits_{{s}_{1}a,{s}_{2}b}{{{\Delta }}}_{{s}_{1},{s}_{2}}^{a,b}({{{{{\bf{k}}}}}}){F}_{{s}_{1}a,{s}_{2}b}^{{{\dagger}} }({{{{{\bf{k}}}}}})+\,{{\mbox{h.c.}}}\,,$$

(1)

where ${F}_{{s}_{1}a,{s}_{2}b}^{{{\dagger}} }({{{{{\bf{k}}}}}})={c}_{{s}_{1}a}^{{{\dagger}} }({{{{{\bf{k}}}}}}){c}_{{s}_{2}b}^{{{\dagger}} }(-{{{{{\bf{k}}}}}})$ is the creation operator of Cooper pairs, s₁, s₂ are indices for spins and a, b are for pseudospins (e.g., two orbitals {1, 2}). A general pairing potential of a two-band model is a four-by-four matrix⁶. In particular, the spin-singlet pairing function ${{{\Delta }}}_{{s}_{1},{s}_{2}}^{a,b}({{{{{\bf{k}}}}}})=f({{{{{\bf{k}}}}}}){M}_{a,b}({{{{{\bf{k}}}}}}){(i{\sigma }_{2})}_{{s}_{1},{s}_{2}}$ consists of the angular form factor f(k) and M_a,b(k) in the orbital channel. The spin-singlet pairings are not mixed with spin-triplet pairings in the absence of spin-orbit coupling (SOC). In analogy to spin-triplet SCs, for the technical convenience, we then use an orbital d_o(k)-vector for the spin-singlet orbital-dependent pairing potential¹¹,

$${\hat{{{\Delta }}}}_{tot}({{{{{\bf{k}}}}}})=[{{{\Delta }}}_{s}{{{\Psi }}}_{s}({{{{{\bf{k}}}}}}){\tau }_{0}+{{{\Delta }}}_{o}({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})](i{\sigma }_{2}),$$

(2)

where Δ_s and Δ_o are pairing strengths in orbital-independent and orbital-dependent channels, respectively. Here τ and σ are Pauli matrices acting on the orbital and spin subspace, respectively, and τ₀ is a 2-by-2 identity matrix. When both Δ_s and Δ_o are real, a real orbital d_o(k)-vector preserves TRS while a complex one spontaneously breaks TRS (${{{{{\mathcal{T}}}}}}=i{\tau }_{0}{\sigma }_{2}{{{{{\mathcal{K}}}}}}$ with ${{{{{\mathcal{K}}}}}}$ being complex conjugate). The Fermi statistics requires Ψ_s(k) = Ψ_s( − k), ${d}_{o}^{1,3}({{{{{\bf{k}}}}}})={d}_{o}^{1,3}(-{{{{{\bf{k}}}}}})$ and ${d}_{o}^{2}({{{{{\bf{k}}}}}})=-{d}_{o}^{2}(-{{{{{\bf{k}}}}}})$. In other words, ${d}_{o}^{2}({{{{{\bf{k}}}}}})$ describes odd-parity spin-singlet orbital-singlet pairings and the other two are for even-parity spin-singlet orbital-triplet pairings. Moreover, we provide an alternative definition of orbital d_o-vectors in Supplementary Note 1. Even though the orbital-independent part Ψ_s(k) is also “orbital-triplet” by statistics, it is completely trivial. Hereafter, we only refer to ${d}_{o}^{1}({{{{{\bf{k}}}}}})$ and ${d}_{o}^{3}({{{{{\bf{k}}}}}})$ as orbital-triplet pairings²⁸.

In addition, the basis functions for both Ψ_s(k) and orbital d_o(k)-vectors in Eq. (2) could be classified by crystalline symmetry.

Under the action of an n-fold rotation operator C_n about the z-axis, the pairing potential $\hat{{{\Delta }}}({{{{{\bf{k}}}}}})$ transforms as

$${{{{{\mathcal{D}}}}}}[{C}_{n}]\,{\hat{{{\Delta }}}}_{J}({{{{{\bf{k}}}}}})\,{({{{{{\mathcal{D}}}}}}[{C}_{n}])}^{T}={e}^{i\frac{2\pi }{n}J}\,{\hat{{{\Delta }}}}_{J}({C}_{n}^{-1}{{{{{\bf{k}}}}}}),$$

(3)

where ${{{{{\mathcal{D}}}}}}[{C}_{n}]$ is the corresponding matrix representation, J is the orbital angular momentum quantum number, and also labels the irreducible representations of the C_n point group. For example, J = 0 is for A representation and J = 2 is for B representation. Firstly, the TRS requires the coexistence of ${\hat{{{\Delta }}}}_{J}$ and ${\hat{{{\Delta }}}}_{-J}$ with equal weight. If the rotation symmetry C_n is further imposed, then J and − J have to be equivalent modulo n, i.e. J ≡ − J mod n. The results for the basis functions of Ψ_s(k) and d_o(k) are summarized in Table 1 for a two-band SC with the {d_xz, d_yz}-orbitals. In this case, ${{{{{\mathcal{D}}}}}}[{C}_{n}]=[\cos (\frac{2\pi }{n}){\tau }_{0}-i\sin (\frac{2\pi }{n}){\tau }_{2}]\otimes {\sigma }_{0}$. For instance, ${{{{{\mathcal{D}}}}}}[{C}_{4}]=-i{\tau }_{2}\otimes {\sigma }_{0}$ explains that both Δ_oτ₁ and Δ_oτ₃ are d-wave-like pairing states²⁹.

Table 1 Classification of spin-singlet pairing potentials for Eq. (2).

At the mean-field level, the Bogoliubov de-Gennes (BdG) Hamiltonian is given by

$$\begin{array}{r}{{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{BdG}}}}}}}=\left(\begin{array}{rc}{{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})&{\hat{{{\Delta }}}}_{tot}({{{{{\bf{k}}}}}})\\ {\hat{{{\Delta }}}}_{tot}^{{{\dagger}} }({{{{{\bf{k}}}}}})&-{{{{{{\mathcal{H}}}}}}}_{0}^{* }(-{{{{{\bf{k}}}}}})\end{array}\right),\end{array}$$

(4)

where ${{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})$ represents a two-band normal-state Hamiltonian with both spin and pseudospin degrees of freedom.

In general, the BdG Hamiltonian is also invariant under the C_n rotation symmetry, i.e., ${{{{{{\mathcal{D}}}}}}}_{{{{{{\rm{BdG}}}}}}}[{C}_{n}]\,{{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{BdG}}}}}}}({{{{{\bf{k}}}}}})\,{({{{{{{\mathcal{D}}}}}}}_{{{{{{\rm{BdG}}}}}}}[{C}_{n}])}^{{{\dagger}} }={{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{BdG}}}}}}}({C}_{n}^{-1}{{{{{\bf{k}}}}}})$ when we define ${{{{{{\mathcal{D}}}}}}}_{{{{{{\rm{BdG}}}}}}}[{C}_{n}]=\left(\begin{array}{rc}{{{{{\mathcal{D}}}}}}[{C}_{n}]&0\\ 0&{e}^{i\frac{2\pi }{n}J}{({{{{{\mathcal{D}}}}}}[{C}_{n}])}^{* }\end{array}\right)$ based on Eq. (3).

Here we assume both inversion and time-reversal symmetries are preserved. To be specific, we consider a SOC-free Hamiltonian,

$${{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})=\epsilon ({{{{{\bf{k}}}}}}){\tau }_{0}{\sigma }_{0}+{\lambda }_{o}({{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){\sigma }_{0},$$

(5)

where the basis is ${\psi }_{{{{{{\bf{k}}}}}}}^{{{\dagger}} }=({c}_{1,\uparrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{1,\downarrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{2,\uparrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{2,\downarrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}))$, $\epsilon ({{{{{\bf{k}}}}}})=({k}_{x}^{2}+{k}_{y}^{2})/2m-\mu$ is the band energy measured relative to the chemical potential μ, m is the effective mass, λ_o represents the orbital hybridization and g_o(k) = (g₁(k), g₂(k), g₃(k)). And the g₃-component leads to the different effective masses of different orbitals. As mentioned earlier, this vector notation is just for the technical convenience. Besides, the g₁ and g₂ components are determined by symmetries. For example, TRS requires g_1,3(k) = g_1,3( − k) and g₂(k) = − g₂( − k). If inversion symmetry (IS) is present, g₂(k) (or g₁(k)) must vanish for ${{{{{\mathcal{I}}}}}}={\tau }_{0}{\sigma }_{0}$ (or ${{{{{\mathcal{I}}}}}}={\tau }_{3}{\sigma }_{0}$), which is the same as the constraint for the orbital d_o-vector. The more explicit form of g_o(k) is determined by other crystal symmetries.

In general, the pseudospin-triplet (i.e. orbital-triplet) pairing state shares some similarities with the spin-triplet pairing state³⁰. To show that, we first discuss the superconducting quasi-particle spectrum of orbital-triplet SCs in the absence of band-splitting caused by orbital hybridizations, i.e., g_o(k) = 0 for Eq. (5). In this case, the superconducting gaps on the Fermi surface are

$$E({{{{{\bf{k}}}}}})=\pm | {{{\Delta }}}_{o}| \sqrt{| {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}}){| }^{2}\pm | {{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\times {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})| },$$

(6)

for the Δ_s = 0 limit. This indicates that there are two distinct gaps if TRS is spontaneously broken. In the following, we mainly focus on the time-reversal-invariant superconducting states, i.e., real d_o-vectors, for which the classification of pairing potentials is shown in Table 1 based on Eq. (3). We will show the interplay between Δ_s and Δ_o can lead to anisotropic superconducting gaps on different Fermi surfaces. Moreover, its stability against orbital-hybridization, electron-electron interactions, and applications to real materials will be discussed in detail as follows. We will also briefly comment on the effects of TRS-breaking in the end.

Stability for spin-singlet orbital-triplet pairings

We apply the weak-coupling scheme⁶ for spin-singlet orbital-triplet pairings against crystal field splittings, which cause orbital hybridizations [i.e. the g_o(k) term in Eq. (5)]. We analytically calculate the superconductivity instability for the orbital d_o-vector by BCS decoupling scheme. The superconducting transition temperature T_c of orbital-dependent pairing channels is calculated by solving the linearized gap equation,

$${{{\Delta }}}_{{s}_{1},{s}_{2}}^{a,b}({{{{{\bf{k}}}}}})= -\frac{1}{\beta }\mathop{\sum}\limits_{{\omega }_{n}}\mathop{\sum}\limits_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}{V}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}^{{s}_{1}a,{s}_{2}b}({{{{{\bf{k}}}}}},{{{{{{\bf{k}}}}}}}^{{\prime} })\\ \times {\left[{G}_{e}({{{{{{\bf{k}}}}}}}^{{\prime} },i{\omega }_{n})\hat{{{\Delta }}}({{{{{{\bf{k}}}}}}}^{{\prime} }){G}_{h}(-{{{{{{\bf{k}}}}}}}^{{\prime} },i{\omega }_{n})\right]}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }},$$

(7)

where β = 1/k_BT, ${G}_{e}({{{{{\bf{k}}}}}},i{\omega }_{n})={[i{\omega }_{n}-{{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})]}^{-1}$ is the Matsubara Green’s function for electrons with ω_n = (2n + 1)π/β and ${G}_{h}({{{{{\bf{k}}}}}},i{\omega }_{n})=-{G}_{e}^{* }({{{{{\bf{k}}}}}},i{\omega }_{n})$. We expand the attractive interactions as ${V}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}^{{s}_{1}a,{s}_{2}b}({{{{{\bf{k}}}}}},{{{{{{\bf{k}}}}}}}^{{\prime} })=-{\sum }_{\Gamma ,l}{[{v}^{\Gamma }{{{{{{\bf{d}}}}}}}_{o}^{\Gamma ,l}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}i{\sigma }_{2}]}_{{s}_{1}a,{s}_{2}b}{[{{{{{{\bf{d}}}}}}}_{o}^{\Gamma ,l}({{{{{{\bf{k}}}}}}}^{{\prime} })\cdot {{{{{\boldsymbol{\tau }}}}}}i{\sigma }_{2}]}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}$ with v^Γ > 0. Here Γ labels the irreducible representation with $l=1,2,...,{{{{{\rm{Dim}}}}}}\,{{\Gamma }}$. In this work we focus on 1d representations, i.e. Dim Γ = 1, which already include many interesting cases and are sufficient for the applications discussed in later sections. Due to the possible existence of multiple pairing channels belonging to different representations, each channel has its own critical temperature ${T}_{c}^{\Gamma }$, the largest of which becomes the actual critical temperature of the system. In the weak-coupling theory, ${T}_{c}^{\Gamma }$ follows the standard BCS form and is solely determined by the corresponding pairing interaction v^Γ in that particular channel. To the leading order of ${\lambda }_{o}{k}_{F}^{2}/\mu$ (${k}_{F}=\sqrt{2m\mu }$), the equation for T_c for the channel Γ reads (see details in the Methods section),

$$\begin{array}{r}\ln \left(\frac{{T}_{c}^{\Gamma }}{{T}_{c0}}\right)={\int}_{\!\!S}d{{\Omega }}\,{{{{{{\mathcal{C}}}}}}}_{0}({T}_{c})\left({\left\vert {{{{{{\bf{d}}}}}}}_{o}^{\Gamma }\right\vert }^{2}-{\left\vert {{{{{{\bf{d}}}}}}}_{o}^{\Gamma }\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}\right\vert }^{2}\right),\end{array}$$

(8)

where T_c0 is the critical temperature for λ_o = 0, Ω is the solid angle of k, ${\hat{{{{{{\bf{g}}}}}}}}_{o}={{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})/| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})|$ are normalized vectors. Here we take ${\int}_{\!\!S}d{{\Omega }}\,| {{{{{{\bf{d}}}}}}}_{o}^{\Gamma }{| }^{2}=1$. And ${{{{{{\mathcal{C}}}}}}}_{0}({T}_{c})=\,{{\mbox{Re}}}\,[{\psi }^{(0)}(\frac{1}{2})-{\psi }^{(0)}(\frac{1}{2}+i\frac{{\lambda }_{o}| {{{{{\bf{g}}}}}}({{{{{\bf{k}}}}}})| }{2\pi {k}_{B}{T}_{c}})]$, where ψ⁽⁰⁾(z) is the digamma function.

We now discuss its implications. In general, the λ_o-term describes a pair-breaking term, since ${{{{{{\mathcal{C}}}}}}}_{0}({T}_{c})\le 0$ and it monotonically decreases as λ_o increases, hence the right-hand side of Eq. (8) suppresses T_c in general. However, if we focus on one-dimensional representations, i.e. Dim Γ = 1, it is straightforward to see that ${{{{{{\bf{d}}}}}}}_{o}^{\Gamma }\parallel {{{{{{\bf{g}}}}}}}_{o}$ can lead to T_c = T_c0 for any value of λ_o, which indicates that the orbital d_o-vector that is parallel with g_o is unaffected by the orbital hybridizations. It is worth mentioning that due to the possible suppression of T_c, depending on the relation between ${{{{{{\bf{d}}}}}}}_{o}^{\Gamma }$ and g_o the leading instability channel at λ_o = 0 could be suppressed more than some of the other coexisting channels and may eventually become sub-leading. This interesting behavior is discussed further in Supplementary Note 3. For notional simplicity, we will drop the representation index Γ when there is no danger of confusion. Choosing ${{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})=(2{k}_{x}{k}_{y},0,{k}_{x}^{2}-{k}_{y}^{2})$, the numerical results are shown in Fig. 1. The black line confirms that T_c is unaffected as ${\lambda }_{o}{k}_{F}^{2}/{k}_{B}{T}_{c0}$ increases for ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})={k}_{F}^{-2}(2{k}_{x}{k}_{y},0,{k}_{x}^{2}-{k}_{y}^{2})$, which is the unconventional A_1g pairing. However, T_c for other d_o-vectors are severely suppressed. The light-blue line is for ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})=\frac{1}{\sqrt{2}}(1,0,1)$, and the light-orange line for ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})={k}_{F}^{-2}({k}_{x}^{2}-{k}_{y}^{2},0,-2{k}_{x}{k}_{y})$. Therefore, we conclude that the orbital d_o-vector could exist in SCs with two active orbitals that are not fully degenerate. This is similar to spin-triplet SCs, where the A_1g-type spin d_s-vector could exist in noncentrosymmetric SCs because d_s∥g_s is optimally satisfied^4,6.

Fig. 1: Stability of orbital d_o-vectors vs orbital hybridization λ_o in Eq. (5).

It shows the transition temperature T_c/T_c0 as a function of ${\lambda }_{o}{k}_{F}^{2}/{k}_{B}{T}_{c0}$ for ${{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})=(2{k}_{x}{k}_{y},0,{k}_{x}^{2}-{k}_{y}^{2})$. T_c0 is T_c at λ_o = 0. The curves from top to bottom correspond to ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})={k}_{F}^{-2}(2{k}_{x}{k}_{y},0,{k}_{x}^{2}-{k}_{y}^{2})$, ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})=\frac{1}{\sqrt{2}}(1,0,1)$, and ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})={k}_{F}^{-2}({k}_{x}^{2}-{k}_{y}^{2},0,-2{k}_{x}{k}_{y})$, respectively.

It is worth mentioning that the results presented above is using a continuum form of the Hamiltonian based on k ⋅ p theory. For real materials, given the interaction on the lattice, the components of the interaction in terms of the basis functions of the representations might not be exactly the same with the form of the vector g_o. As a result, the parallel condition presented above may not be exactly satisfied. However, the theory developed in this work is generally applicable and the extend to which the parallel condition holds can still be a useful criterion for the most favorable pairing.

Next, we include Δ_s, and investigate the coupling between Ψ_s and d_o. Solving the coupled linearized gap equations up to ${({\lambda }_{o}{k}_{F}^{2}/\mu )}^{2}$ order (see details in Supplementary Note 3), we find that the results from Eq. (8) are still correct. Besides, the magnitude of orbital d_o-vectors might be determined as ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})={{{\Psi }}}_{s}({{{{{\bf{k}}}}}}){\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})$. It implies that Ψ_s and d_o belong to the same representation of crystalline groups. Therefore, the stability of orbital d_o-vector by Eq. (8) indicates the symmetry principle for spin-singlet orbital-triplet pairings.

We now explain Eq. (8) from the band picture. Within the band basis, the pairing potential in the orbital subspace becomes ${\hat{{{\Delta }}}}_{{{{{{\rm{band}}}}}}}({{{{{\bf{k}}}}}})={U}^{{{\dagger}} }({{{{{\bf{k}}}}}})\left[{{{\Delta }}}_{s}{{{\Psi }}}_{s}({{{{{\bf{k}}}}}}){\tau }_{0}+{{{\Delta }}}_{o}({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})\right]U({{{{{\bf{k}}}}}})$, where U(k) is the unitary matrix in the orbital subspace, U^†(k)[ϵ(k)τ₀ + λ_o(g_o(k) ⋅ τ)]U(k) = Diag[E₊(k), E₋(k)], with the normal band dispersion

$${E}_{\pm }({{{{{\bf{k}}}}}})=\epsilon ({{{{{\bf{k}}}}}})\pm {\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| .$$

(9)

The intra-orbital pairing naturally gives rise to the intra-band pairing. However, it is different for orbital-dependent pairings. To show that, we decompose the orbital d_o-vector, ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})={d}_{\parallel }({{{{{\bf{k}}}}}}){\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})+{{{{{{\bf{d}}}}}}}_{\perp }({{{{{\bf{k}}}}}})$, where ${d}_{\parallel }({{{{{\bf{k}}}}}})={{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})$ and ${{{{{{\bf{d}}}}}}}_{\perp }({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})=0$. We find that the d_∥-part gives rise to the intra-band pairing, while the d_⊥-part leads to the inter-band pairing (see Supplementary Note 4). If the band splitting is much larger than the pairing gap (${\lambda }_{o}{k}_{F}^{2}\gg {{{\Delta }}}_{o}$), the inter-band pairing is not energetically favorable in the weak-coupling pairing limit. It means that the inter-band pairing will be severely suppressed if we increase the orbital hybridization λ_o, consistent with Eq. (8) and results in Fig. 1. Now if we again include the orbital-independent pairing part Δ_sΨ_s(kτ₀iσ₂), the relation between d_o and Ψ_s(k) obtained previously from solving the coupled linearized gap equation (see Supplementary Note 3) can also be reproduced in the band picture by considering the maximization of the condensation energy. The total condensation energy per volume and per spin of the two intra-band pairings is given by

$$\delta E= \,{N}_{+}\mathop{\sum}\limits_{{{{{{\bf{k}}}}}}\in {{{\mbox{FS}}}}_{+}}{\left({{{\Delta }}}_{s}{{{\Psi }}}_{s}({{{{{\bf{k}}}}}})+{{{\Delta }}}_{o}{d}_{\parallel }({{{{{\bf{k}}}}}})\right)}^{2}\\ +{N}_{-}\mathop{\sum}\limits_{{{{{{\bf{k}}}}}}\in {{{\mbox{FS}}}}_{-}}{\left({{{\Delta }}}_{s}{{{\Psi }}}_{s}({{{{{\bf{k}}}}}})-{{{\Delta }}}_{o}{d}_{\parallel }({{{{{\bf{k}}}}}})\right)}^{2},$$

(10)

where N_± are the density of states on the two Fermi surfaces (E_±). And Δ_sΨ_s(k) ± Δ_od_∥(k) are the pairing gaps on these two Fermi surfaces. In order to maximize δE, we have d_∥(k) = sign[(N₊ − N₋)Δ_sΔ_o]Ψ_s(k) (See Supplementary Note 4 for details). Even though the intra-orbital pairing and the orbital-triplet pairing belong to the same symmetry representation, the different k-dependencies of Ψ_s(k) and d_∥(k) can naturally lead to the anisotropic superconducting gap on the Fermi surface observed in experiments.

Applications to superconductors with/without nodes

As a consequence of the mixing of the orbital-independent pairing (Δ_s) and orbital-dependent pairing (Δ_o) discussed in the previous section, there could be a nodal SC. In this section, we apply the results of the previous section to study superconductors with two orbitals, where Δ_s and Δ_o coexist. It is shown that the anisotropic gap functions with/without nodes depend on the ratio of Δ_s and Δ_o superconducting order parameters. Our weak-coupling theory might have potential applications to some of the nodal/nodeless SCs in the iron-chalcogenides family. For example, the angle-resolved photoemission spectroscopy (ARPES) measurements indicate a nontrivial superconducting gap anisotropy for the monolayer FeSe thin film³¹. The penetration depth measurements on both LaFePO³² and LiFeP³³ show a linear dependence on T, suggesting the presence of superconducting gap nodes.

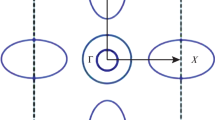
As an example, we consider the pairing potential in Eq. (2) for monolayer FeSe, where there is no hole pocket around the Γ-point, and a two-spin two-orbital model has been shown to be a good approximation around the electron pockets near the M point of the Brillouin zone (two Fe unit cell). The density functional theory calculations show that there are four bands around the M point, giving rise to only two electron pockets. In the one Fe unit cell, there is one pocket near the X and Y points, respectively. After folding with respect to the unit cell with two Fe, we obtain two pockets around the M point. Considering spin degrees of freedom, it naturally resembles a C_4z-invariant two-orbital model³⁴,

$${{{{{{\mathcal{H}}}}}}}_{M}({{{{{\bf{k}}}}}})= \, \left[\epsilon ({{{{{\bf{k}}}}}}){\tau }_{0}+A{k}_{x}{k}_{y}{\tau }_{z}\right]{\sigma }_{0} +{v}_{{{{{{\rm{so}}}}}}}{\tau }_{x}\left[{k}_{x}{\sigma }_{y}+{k}_{y}{\sigma }_{x}\right],$$

(11)

where $\epsilon ({{{{{\bf{k}}}}}})=({k}_{x}^{2}+{k}_{y}^{2})/(2m)-\mu$ with m > 0 the effective mass, A leads to the anisotropic effective mass (i.e., orbital hybridization), and v_so represents SOC that still preserves inversion symmetry. These four states are degenerate at the M point since they form the four-dimensional representation of the space group No. 129 (P4/nmm)³⁵. We take the parameters for the FeSe thin film as μ = 55 meV, 1/(2m) = 1375 meV ⋅ Ų, A = 600 meV ⋅ Ų and v_so≤15 meV ⋅ ų⁴. The SOC is very weak to open a tiny gap along the k_x = 0 and k_y = 0 lines, shown in Fig. 2a. As what we expect, it shows two C_4z rotational-invariant Fermi surfaces, and the maximal gap, which is induced by the z-component of the g_o vector, is around 12 meV along the (11) and (1$\bar{1}$) directions. This is larger than the typical superconducting gaps in iron-chalcogenide SCs (~4 meV), implying that the effect of the orbital hybridization on the pairing symmetries should not be neglected.

Fig. 2: The application to iron-chalcogenide superconductors with/without linear Dirac nodes.

In (a), the two-electron pockets around the M point. For zero spin-orbit coupling, v_so = 0, (b) shows the phase diagram as a function of the intra-orbital pairing Δ_s and the inter-orbital pairing Δ_o. For the gap parameters represented by the green dot in (b), the nodal superconductor is exhibited in (c), where the eight dark red points represent the chiral symmetry-protected Dirac nodes.

We now use the criteria derived above (Eq. (8)) to examine the superconducting states. Specifically, the weak-coupling criterion indicates that the most favorable pairing to characterize the anisotropic superconducting gap is the A_1g-type s-wave pairing symmetry,

$$\hat{{{\Delta }}}({{{{{\bf{k}}}}}})=\left[{{{\Delta }}}_{s}{\tau }_{0}+{{{\Delta }}}_{o}{k}_{x}{k}_{y}{\tau }_{z}\right]\left(i{\sigma }_{2}\right).$$

(12)

The ratio between Δ_s and Δ_o determines the superconducting nodal structure. To simplify the analysis, we turn off the weak SOC. In the band basis, the dispersion of ${{{{{{\mathcal{H}}}}}}}_{M}({{{{{\bf{k}}}}}})$ is ${\epsilon }_{\pm }({{{{{\bf{k}}}}}})=({k}_{x}^{2}+{k}_{y}^{2})/(2m)\pm A| {k}_{x}{k}_{y}| -\mu$. Here ± label the band index. Projecting $\hat{{{\Delta }}}({{{{{\bf{k}}}}}})$ onto the bands leads to Δ_± = Δ_s ± Δ_o∣k_xk_y∣. Given that Δ_s, Δ_o > 0, nodal points can only appear for Δ₋ on the “ − ” band. The nodal condition would be ∣k_xk_y∣ = Δ_s/Δ_o has solution on the FS given by ϵ₋(k) = 0. By using the mathematical inequality ${k}_{x}^{2}+{k}_{y}^{2}\le 2| {k}_{x}{k}_{y}|$, it can be shown that the nodal condition is given by,

$$\frac{{{{\Delta }}}_{s}}{{{{\Delta }}}_{o}}\le \frac{\mu }{1/m-A},$$

(13)

which is shown in Fig. 2b. In general, the ratio Δ_s/Δ_o should depend on both interaction strength in each pairing channel and the orbital hybridization strength. This gives rise to the condition of nodal A_1g-type s-wave superconducting states. Therefore, it could not only explain the anisotropic gap functions observed in the FeSe thin film (fully gapped) but also the nodal superconductivity in LaFePO and LiFeP. Around one linear Dirac node, the effective Hamiltonian up to linear-k can be mapped out as

$${{{{{{\mathcal{H}}}}}}}_{D}={k}_{1}{\tilde{\sigma }}_{0}{\tilde{\tau }}_{z}+{k}_{2}{\tilde{\sigma }}_{y}{\tilde{\tau }}_{y},$$

(14)

where k₁, k₂ are liner combinations of k_x and k_y. All the other Dirac nodes are related to this one by reflection symmetries. Then, we only need to focus on ${{{{{{\mathcal{H}}}}}}}_{D}$, which is a Dirac Hamiltonian with topological charge (winding number) ± 2, whose node is protected by the chiral symmetry (i.e., the product of time-reversal symmetry and particle-hole symmetry). The $2{\mathbb{Z}}$ winding number is due to the presence of inversion symmetry and time-reversal symmetry. To analytically show the topology of Dirac nodes, we apply perturbation analysis with respect to PT symmetry (i.e., the product of time-reversal symmetry and inversion symmetry) and Chiral symmetry. Note that the PT symmetry can be also C_2zT symmetry for a 2D or quasi-2D SC. The projected symmetry representations are given by $\,{{\mbox{PT}}}\,={\tilde{\sigma }}_{y}{\tilde{\tau }}_{0}$ and ${{{{{\mathcal{C}}}}}}={\tilde{\sigma }}_{y}{\tilde{\tau }}_{x}$. As expected, the PT symmetry commutes with ${{{{{{\mathcal{H}}}}}}}_{D}$, while the Chiral symmetry anti-commutes with ${{{{{{\mathcal{H}}}}}}}_{D}$. Then, local perturbations preserving PT and Chiral are

$${{{{{{\mathcal{H}}}}}}}_{D}^{{\prime} }={m}_{1}{\tilde{\sigma }}_{0}{\tilde{\tau }}_{y}+{m}_{2}{\tilde{\sigma }}_{y}{\tilde{\tau }}_{z},$$

(15)

where m₁ and m₂ represent perturbation strengths or mass terms. The spectrum of ${{{{{{\mathcal{H}}}}}}}_{D}+{{{{{{\mathcal{H}}}}}}}_{D}^{{\prime} }$ are given by

$$E=\pm \sqrt{{k}_{1}^{2}+{k}_{2}^{2}+{m}_{1}^{2}+{m}_{2}^{2}\pm 2| {m}_{1}{k}_{2}+{m}_{2}{k}_{1}| },$$

(16)

which indicates that the Dirac nodes are movable but not removable. For example, k₁ = 510.7k_x + 76.5k_y and k₂ = − 14.7k_x − 40.9k_y around one Dirac node. Then, turning on the SOC v_so = 15 meV ⋅ Å, we numerically confirm the nodal SC phase with Δ_s = 3 meV and Δ_o = 200 meV ⋅ Ų, shown in Fig. 2c, where the logarithm of superconducting gaps are plotted. The eight dark red points are the linear Dirac nodes. Based on the topology-protection argument, the interplay between intra- and inter-orbital pairings for nodal superconductivity is robust against local perturbations. Note that our results are different from a previous work³⁴, in which the d-wave pairing symmetry induced nodal SC. In experiments, the nodal gap structure could be detected by measuring the temperature dependence of physical quantities like specific heat and penetration depth at low temperatures. A power law dependence usually indicates the existence of nodal structures (point nodes or line nodes), whereas exponential dependence implies the SC is fully gapped³.

Applications to superconductors with nematic order

In addition to the crystal field splitting, the many-body electron-electron interactions may also lead to orbital hybridization, such as the nematic ordering in the normal states (See Supplementary Note 5 for details). The rotational symmetry reduction could either be from interaction-induced spontaneous symmetry breaking or from explicit symmetry breaking from, say, adding external strain. Then the natural question to ask is whether it is still possible to have an orbital-dependent pairing order characterized by some d_o-vector. Interestingly, we find that the orbital-dependent pairing can coexist with the electronic nematic ordering as long as d_o is parallel to the g_tot, which is an effective orbital-hybridization vector that also contains the nematic order. This establishes a deep connection between SCs with nematic order and spin-singlet orbital-triplet pairings. In the following, we study two typical examples.

• For case A [two-orbital system], we apply the theory to fit the anisotropic superconducting gap of the hole pocket in the bulk FeSe measured by the quasiparticle interference imaging¹².

• For case B [two-valley system], we use a toy model to demonstrate the possible existence of s + d-like nematic nodal superconductor in two-valley systems on a honeycomb lattice. We also show the transition between U-shaped and V-shaped quasi-particle density-of-state by tuning the chemical potential.

Case A: two-orbital model for the bulk FeSe SC

We discussed the possible anisotropic A_1g-type s-wave pairing states for the C₄-symmetric iron-chalcogenide SCs including fully gapped FeSe thin film and nodal SC in LiFeP and LaFePO. Here we investigate the C₄-breaking nematic SC in bulk FeSe. Let us revisit the iron-based SC with a well-established nematic ordering. We consider ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{int}}}}}}}={v}_{1}{\hat{n}}_{1}({{{{{\bf{r}}}}}}){\hat{n}}_{2}({{{{{\bf{r}}}}}})$, where ${\hat{n}}_{i}$ is electron density operator for the i-atomic orbital. If $\langle {\hat{n}}_{1}\rangle \ne \langle {\hat{n}}_{2}\rangle$, C_n (n > 2) is spontaneously broken down to C₂ and we have the nematic order. The intra-orbital interaction does not alter the mean-field results for nematic orders (See Supplementary Note 5). The total inter-orbital hybridization contains two parts,

$${{{{{{\bf{g}}}}}}}_{{{{{{\rm{tot}}}}}}}({{{{{\bf{k}}}}}})={{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})+{{{{{{\bf{g}}}}}}}_{{{{{{\rm{nem}}}}}}},$$

(17)

where g_o(k) is caused by the crystal field splitting and g_nem = (0, 0, Φ) is induced due to the nematicity ${{\Phi }}={v}_{1}\langle {\hat{n}}_{1}-{\hat{n}}_{2}\rangle$, which is momentum-independent if translation symmetry is to be preserved. Hereafter, we focus on the hole pockets around the Γ point to fit the experimental data of superconducting gap functions¹². We will see that even this simplified weak-coupling model, where the coupling between the hole pockets at the Γ point and the electron pockets at the M point is ignored, can produce a descent fit the experimental data. A similar result is expected for the electron pockets near the M point. Replacing g_o with g_tot in Eq. (5), we can still use Eq. (8) to investigate the interplay between superconductivity and nematic order, thus the orbital d_o-vector satisfying d_o∥g_tot leads to the nematic superconductivity. Thus, it generally shows the A_1g-type s-wave spin-singlet orbital-triplet pairings in nematic SCs.

This scenario can be adopted to study the quasi-two dimensional bulk FeSe, where superconductivity (T_c ~ 8 K) emerges inside a well-developed nematic phase (transition temperature T_nem ~ 90 K³⁶), shown in Fig. 3a. For a minimal two-band model³⁷ for the bulk FeSe with {d_xz, d_yz}-orbitals, ${{{{{{\bf{g}}}}}}}_{o}=(2{k}_{x}{k}_{y},0,{k}_{x}^{2}-{k}_{y}^{2})$ and g_nem = (0, 0, Φ)^38,39. Therefore, the nematic orbital d_o-vector with d_o∥g_tot breaks C₄ (see Supplementary Note 5 for more details). The projected pairing gap function on the large Fermi surface is given by

$${{{\Delta }}}_{{{{{{\rm{FS}}}}}}}({{{{{\bf{k}}}}}})={{{\Delta }}}_{s}+{{{\Delta }}}_{o}\sqrt{{(-{\lambda }_{o}({k}_{x}^{2}-{k}_{y}^{2})+{{\Phi }})}^{2}+{(2{\lambda }_{o}{k}_{x}{k}_{y})}^{2}}.$$

(18)

If Φ = 0, Δ_FS(k) is reduced to ${{{\Delta }}}_{s}+{{{\Delta }}}_{o}| {\lambda }_{o}| ({k}_{x}^{2}+{k}_{y}^{2})$ that is in the isotropic limit. The presence of Φ is the driving force for the anisotropy of Δ_FS(k). When the nematicity Φ is strong enough, the orbital d_o-vector will be pinned along the z-axis, resulting in the so-called orbital-selective pairing states. We adopt the realistic parameters for the bulk FeSe SC from Ref. ³⁹ to calculate the superconducting gap measured by the quasiparticle interference imaging¹². In Fig. 3b, we show the angular dependence of the pairing gap around the hole pocket at the Γ-point of FeSe in the presence of nematic order. Our theory provides an equally decent fit to recent experimental data¹² as the intra-orbital s + d-pairing theory proposed by Kang et al.³⁹, even though our work uses a simplified model without considering the coupling to the other two electron pockets. Our theory shows more clearly the role of nematic order on the pairing symmetries. Therefore, the theory developed in this work may alternatively explain the experimental evidence of orbital-selective pairings of the FeSe SC in refs. ^12,27, and reveal a deep connection between nematic SC and spin-singlet orbital-triplet pairings. It has to be mentioned that here we only focused on the hole pockets around the Γ point and discussed the nematicity-induced gap anisotropy around the hole FS. There are other possible mechanisms for gap anisotropy in Fe-based SCs. For example, a previous work⁴⁰ discussed, among other things, the anisotropy/isotropy of the SC gap around the electron pockets at the M point, where the degree of anisotropy depends on the J₁-J₂ magnetic frustration in the proposed five-orbital t-J₁-J₂ microscopic model.

Fig. 3: The application to bulk FeSe superconductors with nematicity.

a Schematic phase diagram vs temperature T for normal metal (T > T_nem), nematic metal (T < T_nem), and nematic superconductivity (T < T_c). b Angular dependence of the superconducting pairing gap: comparison between experiment data (black dots) by Sprau et al. ref. ¹², our theory (red line) and the theory proposed by Kang et al.³⁹ (blue line). Fitting parameters used for our model: Δ_s = 2.6, Δ_o = − 0.055 in Eq. (18). All the other parameters used are the same³⁹, including the chemical potential, effective mass, orbital hybridization, and nematic order.

Case B: two-valley system superconductivity

Similar to the two-orbital systems considered above, we discuss in this section superconductivity in two-valley systems, like single layer graphene SC⁴¹ or transition metal dichalcogenide (TMD)⁴², where the pairing can be between opposite valleys K_±. The spin-singlet pairing is merely characterized by the orbital d_o-vector with Δ_s = 0 in Eq. (2). For the single-particle Hamiltonian, the inter-valley hopping is naturally forbidden by translational symmetry, namely, λ_o = 0 in Eq. (5). Then, we consider the inter-valley scattering Hamiltonian, ${{{{{{\mathcal{H}}}}}}}_{{{{{{\rm{int}}}}}}}={\sum }_{{{{{{\bf{k}}}}}},{{{{{{\bf{k}}}}}}}^{{\prime} },\sigma }V({{{{{\bf{k}}}}}}-{{{{{{\bf{k}}}}}}}^{{\prime} }){c}_{+,\sigma }^{{{\dagger}} }({{{{{\bf{k}}}}}}){c}_{+,\sigma }({{{{{{\bf{k}}}}}}}^{{\prime} }){c}_{-,\sigma }^{{{\dagger}} }({{{{{{\bf{k}}}}}}}^{{\prime} }){c}_{-,\sigma }({{{{{\bf{k}}}}}})$. It generates the inter-valley coupling g_int by defining the order parameter ${{\Phi }}({{{{{\bf{k}}}}}})={\sum }_{{{{{{{\bf{k}}}}}}}^{{\prime} },\sigma }V({{{{{\bf{k}}}}}}-{{{{{{\bf{k}}}}}}}^{{\prime} })\langle {c}_{+,\sigma }({{{{{{\bf{k}}}}}}}^{{\prime} }){c}_{-,\sigma }^{{{\dagger}} }({{{{{{\bf{k}}}}}}}^{{\prime} })\rangle$ that spontaneously breaks the translational symmetry,

$${{{{{{\bf{g}}}}}}}_{{{{{{\rm{int}}}}}}}({{{{{\bf{k}}}}}})=({g}_{{{{{{\rm{int}}}}}},1}({{{{{\bf{k}}}}}}),{g}_{{{{{{\rm{int}}}}}},2}({{{{{\bf{k}}}}}}),0),$$

(19)

where g_int,1(k) = Re[Φ(k)] and g_int,2(k) = − Im[Φ(k)]. In this case, TRS is ${{{{{\mathcal{T}}}}}}=i{\tau }_{1}{\sigma }_{2}{{{{{\mathcal{K}}}}}}$ and IS is ${{{{{\mathcal{I}}}}}}={\tau }_{1}{\sigma }_{0}$. The d_o-vector is manifested as d_o = (d₁(k), id₂(k), 0) with d₁(k) = d₁( − k) and d₂(k) = − d₂( − k). Both d₁(k) and d₂(k) are real to preserve TRS. As for the interaction-induced g_int, ${{{{{\mathcal{T}}}}}}$ and ${{{{{\mathcal{I}}}}}}$ require g_int,1(k) = g_int,1( − k) and g_int,2(k) = 0. By symmetry, there are two general possibilities. One is g_int,1(k) = 1, so ${C}_{3}\times {{{{{\mathcal{I}}}}}}={C}_{6}$ is preserved, and it describes the charge-density-wave order^43,44. The other one is ${g}_{{{{{{\rm{int}}}}}},1}({{{{{\bf{k}}}}}})\in \{{k}_{x}{k}_{y},{k}_{x}^{2}-{k}_{y}^{2}\}$ that spontaneously breaks C₆ down to C₂, forming a nematic order. This is experimentally possible for the strain-induced Kekul’e distortion (i.e., $\sqrt{3}\times \sqrt{3}$ type).

We next discuss superconductivity in the presence of inter-valley couplings, by replacing the g_o-vector in Eq. (5) with the interaction-induced g_int. As a result, Eq. (8) is still applicable. It is similar to a recent work⁴⁵ where the charge order coexists with a sublattice-selective non-unitary pairing state.

The nematic inter-valley coupling is represented as ${g}_{{{{{{\rm{int}}}}}},1}({{{{{\bf{k}}}}}})=1+2{t}_{1}{k}_{x}{k}_{y}+{t}_{2}({k}_{x}^{2}-{k}_{y}^{2})$, which requires that ${{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})=(1+2{t}_{1}{k}_{x}{k}_{y}+{t}_{2}({k}_{x}^{2}-{k}_{y}^{2}),0,0)$ (see Supplementary Note 6). Here the normalization factor has been dropped without changing the essential physics. The system is fully gapped if the s-wave gap is dominant ($1\gg \sqrt{{t}_{1}^{2}+{t}_{2}^{2}}$), otherwise, it is a d-wave dominant nodal SC ($1\ll \sqrt{{t}_{1}^{2}+{t}_{2}^{2}}$).

As a concrete toy model, we look at superconductivity on a generic honeycomb lattice with two valleys K_±, with the Hamiltonian around the two valleys given by,

$${{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})=\epsilon ({{{{{\bf{k}}}}}}){\tau }_{0}{\sigma }_{0}+\alpha \left({k}_{x}^{3}-3{k}_{x}{k}_{y}^{2}\right){\tau }_{3}{\sigma }_{0},$$

(20)

where the two-valley basis used here is given by ${\psi }_{{{{{{\bf{k}}}}}}}^{{{\dagger}} }=({c}_{{K}_{+},\uparrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{{K}_{+},\downarrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{{K}_{-},\uparrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{{K}_{-},\downarrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}))$ and ϵ(k) takes the same form as in Eq. (5). The parameter α determines the C₃ anisotropy of the continuum model around each valley. This Hamiltonian was used as an effective model⁴⁶ to study twisted bilayer graphene.

Including the inter-valley scattering effects, the one-band model is given by

$${{{{{\mathcal{H}}}}}}({{{{{\bf{k}}}}}})= \,\epsilon ({{{{{\bf{k}}}}}}){\tau }_{0}{\sigma }_{0}+\alpha \left({k}_{x}^{3}-3{k}_{x}{k}_{y}^{2}\right){\tau }_{3}{\sigma }_{0} +{\lambda }_{{{{{{\rm{int}}}}}}}[{{{{{{\bf{g}}}}}}}_{{{{{{\rm{int}}}}}}}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}]{\sigma }_{0},$$

(21)

where the λ_int determines the strength of the inter-valley scattering. In Fig. 4, we present representative numerical results for Eq. (21). Panels (a–c) illustrate Fermi surfaces with varying parameters, while panels (d–f) depict the corresponding quasi-particle density of states (DOS).

Fig. 4: Fermi surfaces (FSs) at the K_± valleys and the quasi-particle density of states (DOS).

Panels (a–c) show FSs with varying parameters, while panels (d–f) exhibit the corresponding quasi-particle DOS. The C₆ symmetric FS without inter-valley scattering is shown in (a) and its DOS with an isotropic s-wave pairing is given in (d). b Shows C₆-breaking FSs due to the inter-valley scattering, together with the nodal lines of nematic pairing. There are no nodes on the FSs and the corresponding DOS is shown in (e). c Is similar to (b) but with chemical potential μ adjusted so that the nodal lines intersect the FSs, hence a V-shaped DOS is obtained as in (f). Parameters used are the following, the C₃ anisotropy α = 0.2, the coefficients for basis functions t₁ = 0.15, t₂ = 0.25, the orbitial-dependent pairing gap Δ_o = 0.5. For (a) and (d) μ = 1.5 (chemical potential), the inter-valley coupling g_int = 0; for (b) and (e) μ = 1.5, g_int = 0.7; for (c) and (f) μ = 2.7, g_int = 0.7.

In the absence of inter-valley scattering (λ_int = 0), the Fermi surfaces (FSs) around the two K_± valleys are plotted in Fig. 4a. As expected, with a fully symmetric s-wave pairing characterized by d_o = (1, 0, 0), a fully gapped or U-shaped quasi-particle density-of-states (DOS) is obtained and shown in Fig. 4d. Then we include the aforementioned inter-valley scattering g_int that breaks C₆ down to C₂. As a result, our theory implies that the effective nematicity generated will favor a nematic pairing characterized by d_o∥g_int. Consider the generic form ${{{{{{\bf{d}}}}}}}_{o}={{{{{{\bf{g}}}}}}}_{{{{{{\rm{int}}}}}}}=(1+2{t}_{1}{k}_{x}{k}_{y}+{t}_{2}({k}_{x}^{2}-{k}_{y}^{2}),0,0)$, the resulting C₆-breaking FS are shown in Fig. 4b, c, where the nodal lines of the pairing are also shown. By tuning the chemical potential μ, the FSs and nodal lines can go from non-intersecting in Fig. 4b to intersecting in Fig. 4c, leading to the corresponding evolution from the gapped U-shaped DOS in Fig. 4e to the gapless V-shaped DOS in Fig. 4f. Our results may explain the experimental observations in magic-angle twist bilayer graphene that reports the nematic order⁴⁷, and V-shaped DOS⁴⁸ at the specific doping level.

Discussions

We briefly discuss the difference between our theory and the previous studies²¹ for nematic SCs. One example is a pairing state belonging to a 2D irreducible representation (Irrep), e.g., the E-pairing in Cu or Nb-doped Bi₂Se₃^49,50 and UPt₃^51,52. A real order parameter vector (Δ_E,1, Δ_E,2) spontaneously breaks C₃, leading to nematic superconductivity. Alternatively, a nematic SC can be formed by mixing two different 1D-Irrep-pairing channels. In FeSe^53,54, the nematic order breaks the C₄ down to C₂, which mixes the s-wave and d-wave pairing channels. However, T_c of the (s + d) orbital-independent pairing state could be generally affected by increasing nematicity, because of the significant change in the density of states at the Fermi energy. In our theory, the (s + d)-like nematic d_o-vector coexists with the nematic order, so T_c is almost unaffected by increasing nematicity. Therefore, it may help to distinguish our results from previous proposals in experiments, where one may use the chemical or physical pressures to tune the nematicity and measure T_c as a function of pressure⁵⁵. Nevertheless, more efforts are necessary to test the results established in this work for nematic SCs.

In addition to the above discussions for the time-reversal-invariant superconducting states, we also comment on the effects of the spontaneous TRS-breaking, where a complex orbital d_o-vector generates the orbital orderings as M_o = − iγ₁/α_M(d × d^*), of which only the y-component breaks TRS (see details in Supplementary Note 7), as illustrated in Fig. 5a. Alternatively, the corresponding quasi-particle spectrum in Fig. 5b shows the two distinct gaps, similar to the range given by Eq. (6). More explicitly, we schematically plot the atomic orbital-polarized density of states (DOS) by defining $\left\vert \pm \right\rangle =\left\vert 1\right\rangle +i\left\vert 2\right\rangle$ for complex orbitals, where D₊ ≠ D₋ at finite energy clearly indicates that the DOS is orbital-polarized, which is consistent with the Ginzburg-Landau theory, shown in Supplementary Note 2. Moreover, we also find that the orbital-spin conversion would lead to the spin-polarized DOS⁵⁶.

Fig. 5: Schematic diagrams for the time-reversal symmetry (TRS) breaking effects.

a, b Are for orbital-triplet superconductors (SCs), while (c) and (d) are for spin-triplet SCs. As for orbital-triplet SCs characterized by a d_o-vector, (a) shows a complex orbital d_o-vector that spontaneously breaks TRS and results in the TRS-breaking orbital-polarization ${{{{{{\bf{M}}}}}}}_{o}\propto i{{{{{{\bf{d}}}}}}}_{o}\times {{{{{{\bf{d}}}}}}}_{o}^{* }$; and (b) shows the quasi-particle spectrum along k_x and the orbital-polarized density of states (DOS) D_± with $\left\vert \pm \right\rangle$ representing $\left\vert 1\right\rangle \pm i\left\vert 2\right\rangle$. As a comparison, in spin-triplet SCs, (c) shows the superconductivity-induced spontaneous spin-polarization ${{{{{{\bf{M}}}}}}}_{s}\propto i{{{{{{\bf{d}}}}}}}_{s}\times {{{{{{\bf{d}}}}}}}_{s}^{* }$; and (d) shows the two distinct gaps of the quasi-particle spectrum along k_x and the spin-polarized DOS D_σ with σ = {↑, ↓}. The gapped spectrum is plotted for k_z ≠ 0 and the node in DOS profile is due to the nodal line at k_z = 0.

The above result for orbital-triplet pairings is similar to the superconducting gaps for non-unitary spin-triplet SCs³. By symmetry, the Gizburg-Landau free energy is the same. To show the similarity, for the single-band spin-triplet SCs⁵⁷, the spin-triplet pairing potential is generally given by $\hat{{{\Delta }}}({{{{{\bf{k}}}}}})={{{\Delta }}}_{0}[{{{{{{\bf{d}}}}}}}_{s}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\sigma }}}}}}](i{\sigma }_{2})$, where Δ₀ is the pairing strength and σ are Pauli matrices in the spin subspace. Due to the Fermi statistics, the spin d_s(k)-vector has to satisfy d_s(k) = − d_s( − k). The d_s-vector formalism is firstly developed for He³ superfluid⁵⁸. And it also occurs in noncentrosymmetric SCs, the spin d_s(k)-vector is usually pinned along a certain crystal axis since superconductivity is non-suppressed only for d_s(k)∥g_s(k), where g_s(k) represents the Rashba spin-orbit coupling (SOC)^4,6. Besides, there is intrinsic spontaneous spin-polarization induced by the non-unitary pairing, d_s(k) = k_z(1, − iη₀, 0) with real η₀. Fig. 5c shows the spin expectation value of the Cooper pairs (${{{{{{\bf{M}}}}}}}_{s}\propto i{{{{{{\bf{d}}}}}}}_{s}^{* }({{{{{\bf{k}}}}}})\times {{{{{{\bf{d}}}}}}}_{s}({{{{{\bf{k}}}}}})=2{\eta }_{0}{k}_{z}^{2}{\overrightarrow{e}}_{z}$). It is an equal-spin pairing so that σ₃ is conserved, and non-zero M_s leads to two distinct superconducting gaps of the quasi-particle spectrum⁵⁹, shown in Fig. 5d. In addition, the density of states (DOS) is spin-polarized, namely, D_↑ ≠ D_↓ at finite energy ω, as illustrated in Fig. 5d.

To summarize, we have derived a general weak-coupling criterion to investigate the spin-singlet orbital-triplet pairings in nematic SCs. For technical convenience, we adopt the orbital d_o-vector to describe the spin-singlet orbital-dependent pairing states and the g_o-vector for the orbital hybridizations. The main results of this work include, first, we demonstrate that an orbital d_o-vector that is parallel with g_o-vector for orbital hybridizations is possible to be realized in real superconducting materials. Second, the interplay between intra-orbital and orbital-dependent pairings that belong to the same symmetry representation can explain the observation of robust Dirac nodes in the quasi-2D iron-based SCs. Remarkably, we find that d_o-vectors could even coexist with many-body interaction-induced nematic orders or charge-density-wave orders when d_o ∝ g_tot = g_o + g_nem (or g_int). Moreover, our theory discovers the important role of nematic orders in SC pairing symmetry, which builds a possible bridge between repulsive interaction-induced nematic orders and nematic superconductivity and also reveals a deep connection between spin-singlet orbital-triplet pairings in nematic SCs. Our results may be helpful in understanding the nematic superconductivity in bulk FeSe. Our work will motivate more theoretical and experimental efforts to search for spin-singlet orbital-triplet SCs, even for topological superconductivity, which might contribute to further understanding the effects of spontaneous symmetry breaking on superconductivity.

Methods

Here we present the derivation for the main result Eq. (8), which is first order in λ_o, by solving the linearized gap equation. The second-order results are presented in Supplementary Note 3. The general k ⋅ p normal Hamiltonian considered in the main text reads,

$${{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})=\epsilon ({{{{{\bf{k}}}}}}){\tau }_{0}{\sigma }_{0}+{\lambda }_{o}({{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){\sigma }_{0},$$

(22)

where the electronic basis is made of {1, 2}-orbitals ${{{\Psi }}}_{{{{{{\bf{k}}}}}}}^{{{\dagger}} }=({c}_{1,\uparrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{1,\downarrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{2,\uparrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}),{c}_{2,\downarrow }^{{{\dagger}} }({{{{{\bf{k}}}}}}))$, $\epsilon ({{{{{\bf{k}}}}}})=({k}_{x}^{2}+{k}_{y}^{2})/2m-\mu$ is the band energy measured relative to the chemical potential μ, λ_o represents the orbital hybridization and g_o(k) = (g₁(k), g₂(k), g₃(k)). The TRS ${{{{{\mathcal{T}}}}}}=i{\sigma }_{2}{\tau }_{0}{{{{{\mathcal{K}}}}}}$ requires g_1,3(k) = g_1,3( − k) and g₂(k) = − g₂( − k). It leads that

$${{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}={\left[{{{{{{\bf{g}}}}}}}_{o}(-{{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}\right]}^{* }.$$

(23)

Besides, we set λ_o > 0 without loss of generality. The Matsubara Green’s function for electrons is ${G}_{e}({{{{{\bf{k}}}}}},i{\omega }_{n})={[i{\omega }_{n}-{{{{{{\mathcal{H}}}}}}}_{0}({{{{{\bf{k}}}}}})]}^{-1}$ and that for holes is ${G}_{h}({{{{{\bf{k}}}}}},i{\omega }_{n})=-{G}_{e}^{* }({{{{{\bf{k}}}}}},i{\omega }_{n})$. Here β = 1/k_BT and ω_n = (2n + 1)π/β with n integer. Therefore,

$${G}_{e}({{{{{\bf{k}}}}}},i{\omega }_{n})= \frac{{{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})}{i{\omega }_{n}-\epsilon ({{{{{\bf{k}}}}}})+{\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| }+\frac{{{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}})}{i{\omega }_{n}-\epsilon ({{{{{\bf{k}}}}}})-{\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| }\\ \triangleq {G}_{e}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n}){{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})+{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}}),$$

(24)

$${G}_{h}(-{{{{{\bf{k}}}}}},i{\omega }_{n})= \frac{{{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})}{i{\omega }_{n}+\epsilon ({{{{{\bf{k}}}}}})-{\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| }+\frac{{{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}})}{i{\omega }_{n}+\epsilon ({{{{{\bf{k}}}}}})+{\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| }\\ \triangleq {G}_{h}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n}){{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})+{G}_{h}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}}),$$

(25)

where ${{{{{{\mathcal{P}}}}}}}_{\pm }({{{{{\bf{k}}}}}})=\frac{1}{2}(1\pm {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})$ with ${\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})={{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})/| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})|$. Here ${G}_{e}^{\pm }({{{{{\bf{k}}}}}},i{\omega }_{n})=\frac{1}{i{\omega }_{n}-\epsilon ({{{{{\bf{k}}}}}})\mp {\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| }$ and ${G}_{h}^{\pm }({{{{{\bf{k}}}}}},i{\omega }_{n})=\frac{1}{i{\omega }_{n}+\epsilon ({{{{{\bf{k}}}}}})\pm {\lambda }_{o}| {{{{{{\bf{g}}}}}}}_{o}({{{{{\bf{k}}}}}})| }$. We expand the attractive interactions as

$${V}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}^{{s}_{1}a,{s}_{2}b}({{{{{\bf{k}}}}}},{{{{{{\bf{k}}}}}}}^{{\prime} })= -\mathop{\sum}\limits_{\Gamma ,l}{v}_{0}^{\Gamma }{[{{{{{{\bf{d}}}}}}}_{o}^{\Gamma ,l}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}i{\sigma }_{2}]}_{{s}_{1}a,{s}_{2}b}\\ \times {[{{{{{{\bf{d}}}}}}}_{o}^{\Gamma ,l}({{{{{{\bf{k}}}}}}}^{{\prime} })\cdot {{{{{\boldsymbol{\tau }}}}}}i{\sigma }_{2}]}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }},$$

(26)

where ${v}_{0}^{\Gamma } > 0$ is the interaction strength of the irreducible representation channel Γ of the crystalline group, and $l=1,2,...,{{{{{\rm{Dim}}}}}}\,{{\Gamma }}$. Each pairing channel Γ gives rise to an SC critical temperature ${T}_{c}^{\Gamma }$, and the actual transition temperature of the system is given by the largest of these critical temperatures. In our work, we mainly focus on the case where ${{{{{\rm{Dim}}}}}}\,{{\Gamma }}=1$, which is sufficient for the applications discussed in the main text. The coupling between orbital-dependent pairings and orbital-independent pairings will be discussed in detail later. The transition temperature ${T}_{c}^{\Gamma }$ of orbital-dependent pairing channels is calculated by solving the linearized gap equation,

$${{{\Delta }}}_{{s}_{1},{s}_{2}}^{a,b}({{{{{\bf{k}}}}}})= -\frac{1}{\beta }\mathop{\sum}\limits_{{\omega }_{n}}\mathop{\sum}\limits_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}{V}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }}^{{s}_{1}a,{s}_{2}b}({{{{{\bf{k}}}}}},{{{{{{\bf{k}}}}}}}^{{\prime} })\\ \times {\left[{G}_{e}({{{{{{\bf{k}}}}}}}^{{\prime} },i{\omega }_{n})\hat{{{\Delta }}}({{{{{{\bf{k}}}}}}}^{{\prime} }){G}_{h}(-{{{{{{\bf{k}}}}}}}^{{\prime} },i{\omega }_{n})\right]}_{{s}_{1}^{{\prime} }{a}^{{\prime} },{s}_{2}^{{\prime} }{b}^{{\prime} }},$$

(27)

which is reduced to ${v}_{0}^{\Gamma }{\chi }^{\Gamma }(T)-1=0$ with the superconductivity susceptibility χ^Γ(T) in the channel Γ defined as,

$${\chi }^{\Gamma }(T)=-\frac{1}{\beta }\mathop{\sum}\limits_{{{{{{\bf{k}}}}}},{\omega }_{n}}\,{{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}^{\Gamma }({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}i{\sigma }_{2})}^{{{\dagger}} }{G}_{e}({{{{{\bf{k}}}}}},i{\omega }_{n})({{{{{{\bf{d}}}}}}}_{o}^{\Gamma }({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}i{\sigma }_{2}){G}_{h}(-{{{{{\bf{k}}}}}},i{\omega }_{n})\right],$$

(28)

$$= -\frac{2}{\beta }\mathop{\sum}\limits_{{{{{{\bf{k}}}}}},{\omega }_{n}}\mathop{\sum}\limits_{\alpha ,\beta }{G}_{e}^{\alpha }({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{\beta }({{{{{\bf{k}}}}}},i{\omega }_{n})\\ \times \,{{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}^{\Gamma }({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})}^{{{\dagger}} }{{{{{{\mathcal{P}}}}}}}_{\alpha }({{{{{\bf{k}}}}}})({{{{{{\bf{d}}}}}}}_{o}^{\Gamma }({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){{{{{{\mathcal{P}}}}}}}_{\beta }({{{{{\bf{k}}}}}})\right],$$

(29)

where α, β ∈ { + , − }. For notional simplicity, the superscript Γ will be dropped when there is no danger of confusion. Firstly, let us calculate the trace part. In the following calculation, we will use

$$ {{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})}^{{{\dagger}} }{{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}})({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}})\right]\\ +\,{{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})}^{{{\dagger}} }{{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})\right]\\ =\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)+2\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right.\\ \left.\;\;\;\;\;\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right).$$

(30)

And,

$$ {{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})}^{{{\dagger}} }{{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}})({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})\right] \\ +\,{{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})}^{{{\dagger}} }{{{{{{\mathcal{P}}}}}}}_{-}({{{{{\bf{k}}}}}})({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){{{{{{\mathcal{P}}}}}}}_{+}({{{{{\bf{k}}}}}})\right]\\ = \left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)-2\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\\ \;\;\;\;+\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right).$$

(31)

Therefore, we arrive at

$$ {{\mbox{Tr}}}\,\left[{({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}})}^{{{\dagger}} }{{{{{{\mathcal{P}}}}}}}_{\alpha }({{{{{\bf{k}}}}}})({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {{{{{\boldsymbol{\tau }}}}}}){{{{{{\mathcal{P}}}}}}}_{\beta }({{{{{\bf{k}}}}}})\right]\\ = \frac{1}{2}\left[\right.\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)+i\alpha \left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot \left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\times {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right)\\ +i\beta \left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot \left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\times {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right)\\ + \alpha \beta \left(2\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right.\\ \left.-\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right)\left]\right..$$

(32)

Then we have

$$\chi (T) = -\frac{1}{\beta }\mathop{\sum}\limits_{{{{{{\bf{k}}}}}},{\omega }_{n}}\mathop{\sum}\limits_{\alpha ,\beta }{G}_{e}^{\alpha }({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{\beta }({{{{{\bf{k}}}}}},i{\omega }_{n})\left[\right.\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\\ +i\alpha \left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot \left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\times {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right)+i\beta \left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot \left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\times {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right)\\ + \alpha \beta \left(2\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right.\\ \left.-\left({{{{{{\bf{d}}}}}}}_{o}^{* }({{{{{\bf{k}}}}}})\cdot {{{{{{\bf{d}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\left({\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}({{{{{\bf{k}}}}}})\right)\right)\left]\right..$$

(33)

Next, we calculate the integration for ${\sum }_{{{{{{\bf{k}}}}}},{\omega }_{n}}$ by using,

$$\mathop{\sum}\limits_{{{{{{\bf{k}}}}}},{\omega }_{n}}\to \frac{{N}_{0}}{4}\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon {\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }\,\mathop{\sum}\limits_{{\omega }_{n}},$$

(34)

where N₀ is the density of states at Fermi surface and Ω is the solid angle of k on Fermi surfaces. Then,

$$ -\frac{{N}_{0}}{\beta }\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon {\int}_{\!\!S}\frac{d{{\Omega }}}{2\pi }\mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ =-\frac{{N}_{0}}{\beta }\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon {\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }\mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ \equiv {\chi }_{0}(T),$$

(35)

On one hand,

$$\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}} d\epsilon \mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ =\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon \mathop{\sum}\limits_{{\omega }_{n}}\frac{1}{i{\omega }_{n}+\epsilon }\frac{1}{i{\omega }_{n}-\epsilon }\\ =\beta \int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon \frac{\tanh \frac{\beta \epsilon }{2}}{2\epsilon }\\ =\beta \int\nolimits_{0}^{\beta {\omega }_{D}/2}dx\frac{\tanh x}{x}\approx \beta \ln \left(\frac{2{e}^{\gamma }{\omega }_{D}}{\pi {k}_{B}T}\right),$$

(36)

where the approximation is done at low temperature when β → ∞.

On the other hand, we could find a series representation for χ₀, which also applies to the case where λ_o ≠ 0, so that χ₀ ≡ χ(λ_o = 0) and χ(λ_o ≠ 0) can be related by a simple relation. The way to do it is to perform the integration in ϵ first. More precisely,

$$ \int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon \mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ =\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}\mathop{\sum}\limits_{{\omega }_{n}}\frac{1}{i{\omega }_{n}+\epsilon }\frac{1}{i{\omega }_{n}-\epsilon }\\ =2{{{{{\rm{Re}}}}}}\mathop{\sum}\limits_{n\ge 0}\int\nolimits_{-{\omega }_{D}}^{{\omega }_{D}}d\epsilon \frac{1}{i{\omega }_{n}+\epsilon }\frac{1}{i{\omega }_{n}-\epsilon }\\ =2\beta {{{{{\rm{Re}}}}}}\mathop{\sum}\limits_{n\ge 0}\int\nolimits_{-\beta {\omega }_{D}}^{\beta {\omega }_{D}}d\epsilon \frac{1}{i2\pi (n+1/2)+\epsilon }\frac{1}{i2\pi (n+1/2)-\epsilon }\\ \approx 2\beta {{{{{\rm{Re}}}}}}\mathop{\sum}\limits_{n\ge 0}\int\nolimits_{-\infty }^{\infty }d\epsilon \frac{1}{i2\pi (n+1/2)+\epsilon }\frac{1}{i2\pi (n+1/2)-\epsilon }\\ =\beta {{{{{\rm{Re}}}}}}\mathop{\sum}\limits_{n\ge 0}\frac{1}{n+1/2},$$

(37)

where the low-temperature limit is again assumed and the integration is done using the residue theorem. In the same spirit, we have,

$$ \int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}} d\epsilon \mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ =\beta {{{{{\rm{Re}}}}}}\mathop{\sum}\limits_{n\ge 0}\frac{1}{n+1/2+i\frac{{\lambda }_{o}| {{{{{\bf{{g}}}}}_{o}}}({{{{{\bf{k}}}}}})| }{2\pi {k}_{B}T}},$$

(38)

Now by introducing the digamma function defined on the complex plane,

$${\psi }^{(0)}(z)=-\gamma +\mathop{\sum}\limits_{n\ge 0}\left(\frac{1}{n+1}-\frac{1}{n+z}\right),$$

(39)

we have the following relation,

$$ \int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon \mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ -\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon \mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ =\beta \,{{\mbox{Re}}}\, \left[{\psi }^{(0)}\left(\frac{1}{2}\right)-{\psi }^{(0)}\left(\frac{1}{2}+i\frac{{\lambda }_{o}| {{{{{\bf{g}}}}}}({{{{{\bf{k}}}}}})| }{2\pi {k}_{B}T}\right)\right]\\ \equiv \beta {{{{{{\mathcal{C}}}}}}}_{0}(T),$$

(40)

where ${\chi }_{0}(T)={N}_{0}\ln \left(\frac{2{e}^{\gamma }{\omega }_{D}}{\pi {k}_{B}T}\right)$, γ = 0.57721 ⋯   is the Euler-Mascheroni constant and ω_D is the Debye frequency.

Therefore,

$$ -\frac{{N}_{0}}{\beta }\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon {\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }\mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ =-\frac{{N}_{0}}{\beta }\int\nolimits_{-{\omega }_{D}}^{+{\omega }_{D}}d\epsilon {\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }\mathop{\sum}\limits_{{\omega }_{n}}{G}_{e}^{+}({{{{{\bf{k}}}}}},i{\omega }_{n}){G}_{h}^{-}({{{{{\bf{k}}}}}},i{\omega }_{n})\\ ={\chi }_{0}(T)+{N}_{0}{\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }{{{{{{\mathcal{C}}}}}}}_{0}(T).$$

(41)

Now we can proceed to calculate χ(T) given in Eq. (33),

$$\chi (T)= {\chi }_{0}(T){\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }{\left\vert {{{{{{\bf{d}}}}}}}_{o}\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}\right\vert }^{2}$$

(42)

$$\quad +{\chi }_{0}(T){\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }\left(| {{{{{{\bf{d}}}}}}}_{o}{| }^{2}-{\left\vert {{{{{{\bf{d}}}}}}}_{o}\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}\right\vert }^{2}\right)$$

(43)

$$\quad +{N}_{0}{\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }{{{{{{\mathcal{C}}}}}}}_{0}(T)\left(| {{{{{{\bf{d}}}}}}}_{o}{| }^{2}-{\left\vert {{{{{{\bf{d}}}}}}}_{o}\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}\right\vert }^{2}\right)$$

(44)

$$={\chi }_{0}(T)+{N}_{0}{\int}_{\!\!\!\!S}\frac{d{{\Omega }}}{2\pi }\,{{{{{{\mathcal{C}}}}}}}_{0}(T)\left({\left\vert {{{{{{\bf{d}}}}}}}_{o}\right\vert }^{2}-{\left\vert {{{{{{\bf{d}}}}}}}_{o}\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}\right\vert }^{2}\right).$$

(45)

In the calculation, we use normalized gap functions with ${\int}_{\!\!S}\frac{d{{\Omega }}}{2\pi }\,{{{{{{\bf{d}}}}}}}_{o}^{* }\cdot {{{{{{\bf{d}}}}}}}_{o}=1$. It leads to,

$$\ln \left(\frac{{T}_{c}}{{T}_{c0}}\right)={\int}_{\!\!S}\frac{d{{\Omega }}}{2\pi }\,{{{{{{\mathcal{C}}}}}}}_{0}({T}_{c})\left({\left\vert {{{{{{\bf{d}}}}}}}_{o}\right\vert }^{2}-{\left\vert {{{{{{\bf{d}}}}}}}_{o}\cdot {\hat{{{{{{\bf{g}}}}}}}}_{o}\right\vert }^{2}\right),$$

(46)

where T_c0 is T_c for λ_o = 0 case by solving v₀χ₀(T_c0) = 1. This is the Eq. (8) in the main text. In general, the right-hand side of Eq. (46) suppresses T_c. It clearly indicates that T_c would not be suppressed by orbital hybridization once d_o∥g_o for all k. So we conclude that the orbital d_o-vector is possible to be stabilized in materials.