Introduction

Quantum state discrimination, or hypothesis testing, was first introduced by Helstrom1. It can be described in terms of a simple two party game. Alice sends M copies of one of two states, ρ+ or ρ−, to Bob, with some specified prior probability. Bob then tries to implement the optimal measurement to decide which state he has received according to some figure of merit. Owing to the no-cloning theorem2 if the two states to be distinguished are not orthogonal, they can’t be distinguished perfectly. This means that there will necessarily be some error when Bob decides which state he has received. Typically, Bob tries to minimise the average probability of error. When distinguishing between two pure orthogonal states, it is known that a single separable measurement, consisting of only local operations and classical communication (LOCC), can distinguish between the two states perfectly3. (Note that while LOCC usually refers to operations and communication between two parties Alice and Bob, in this work local operations means operations on a single mode of Bob’s state and classical communication means Bob cannot implement entangling operations between the different modes of the state he receives.)

The situation becomes considerably more interesting when considering non-orthogonal states. For distinguishing multiple pure non-orthogonal states, it was first conjectured by Peres and Wooters that collective measurements can improve the error probability compared to LOCC measurements4. A collective measurement here refers to an entangling measurement acting on M copies of the state, \({\rho }_{+}^{\otimes M}\) or \({\rho }_{-}^{\otimes M}\), simultaneously. In contrast, a LOCC measurement means that the M copies of the state received by Bob are measured individually, and each subsequent measurement may be adaptively updated based on previous measurement results. Hence, collective measurements are more general than LOCC measurements. For distinguishing a continuous spectrum of different quantum states given a finite number of copies, the advantage of collective measurements over separable measurements has been confirmed5. However, for distinguishing two non-orthogonal pure states, it is known that collective measurements offer no advantage over separable measurements6,7,8.

When we consider distinguishing between mixed states, the situation becomes more interesting again. For distinguishing two mixed states, collective measurements generally offer an advantage over separable measurements. Despite theoretical progress on the role of collective measurements for discriminating between mixed states9,10,11,12, experimental progress along this avenue has been limited. A great deal of experimental work has focused on optimally distinguishing single copies of pure states13,14,15,16,17,18,19,20,21 or using adaptive separable measurements to distinguish multiple copies of either pure22 or mixed23 states. The multi-copy discrimination of coherent and thermal states was considered recently24. However, in this case, the multiple copies were measured individually, not with a collective measurement and the multi-copy part refers only to the decision making process.

Thus, all previous state discrimination experiments have been limited to LOCC measurements which may not attain the ultimate limits for distinguishing non-orthogonal mixed states. A major reason for this is that collective measurements are difficult to implement experimentally. Indeed, although collective measurements are known to aid a range of tasks in quantum information, including quantum metrology25, Bell violations26 and entanglement distillation27, they have only recently been experimentally demonstrated28,29,30. (It is worth noting that there are other tasks which benefit from measurements in an entangled basis, not necessarily on multiple copies of the same quantum state, including some quantum metrology problems31, quantum orienteering32,33,34 and quantum communications35,36.) The advantage of collective measurements is thus far restricted to performing collective measurements on only two copies of a quantum state30. Previous investigations into the use of collective measurements for state discrimination suggest that collective measurements only offer an advantage over LOCC measurements when measuring at least three copies of the quantum state simultaneously10,11,23. However, as we shall show, this is only true when the prior probabilities for the unknown state being either ρ+ or ρ− are equal.

In this work, we bypass these difficulties and experimentally demonstrate state discrimination enhanced by collective measurements. That is, we implement a collective measurement which distinguishes between two copies of a qubit state with some known prior probability, either \({\rho }_{+}^{\otimes 2}\) or \({\rho }_{-}^{\otimes 2}\), with an error probability lower than what is possible by any LOCC measurement on the same states. A conceptual schematic of both two-copy LOCC and two-copy collective measurements is shown in Fig. 1. To realise our goal, we first find a regime where two copy collective measurements are able to outperform any LOCC measurement. This is done through the dynamic programming approach introduced in previous works23. We then convert the optimal collective measurements to quantum circuits using existing techniques30,37. The same process is followed when implementing three- and four-collective measurements. Finally, these quantum circuits are implemented on the Fraunhofer IBM Q System One (F-IBM QS1) processor. This is in line with a recent trend of using such processors to test otherwise hard to reach aspects of quantum physics, such as quantum metrology30,38, quantum foundations39,40,41, quantum chemistry42,43, quantum optics44 and quantum network simulations45.

Fig. 1: Schematic for optimal separable and collective measurement state discrimination with two copies.
figure 1

a The optimal local operations and classical communication (LOCC) measurement when discriminating two copies of a quantum state involves only local operations on each qubit and classical communication of the measurement results. The measurement angle ϕ1 is chosen prior to the experiment to minimise the expected probability of error. Based on the measurement outcome obtained when measuring the first copy, the optimal ϕ2 is chosen for the second copy, i.e. ϕ2 = ϕ2(ϕ1). A decision of whether the unknown state is ρ+ or ρ− is made based on the outcome of the second measurement. b The optimal collective measurement for discriminating two copies of a quantum state requires entangling operations. The decision about what state is present is made based on all measurement results. c Quantum circuit used to implement the optimal collective measurements shown in b. The U gates correspond to arbitrary single qubit unitary matrices and the Ry and Rz gates correspond to single qubit rotations. The parameters of the circuit are numerically optimised to implement the optimal measurement for a given set of parameters (q, α, v).

Full size image

Results

Theoretical results

Theoretical model

We follow the model of Higgins et al.11, where we wish to discriminate between the two qubit states described by

$${\rho }_{\pm }=\frac{1}{2}\left({{\mathbb{I}}}_{2}+(1-v)({\sigma }_{3}\cos (\alpha )\pm {\sigma }_{1}\sin (\alpha ))\right)\ ,$$
(1)

where \({{\mathbb{I}}}_{2}\) is the 2 × 2 identity matrix, σi denotes the ith Pauli matrix, and v and α describe the extent to which the state is mixed and the angle between the two states in Hilbert space respectively. Note that v = 0 corresponds to a pure state and v = 1 represents the maximally mixed state. Given M copies of the above state, \({\rho }_{\pm }^{\otimes M}\), our task is to decide which state we are given with the minimum probability of error. Denoting the prior probability for the unknown state to be the state ρ+ as q, the error probability is given by

$${P}_{{{{{{{{\rm{e}}}}}}}}}=q{P}_{-| +}+(1-q){P}_{+| -}\ ,$$
(2)

where P−∣+ is the probability of guessing the state ρ− when given the state ρ+ and P+∣− is similarly defined.

Optimal collective measurement

In general, the optimal measurement to distinguish \({\rho }_{\pm }^{\otimes M}\), will be a collective measurement that involves entangling operations between all M modes. The minimum error probability, in this case, is given by the Helstrom bound1

$${P}_{{{{{{{{\rm{e,Col}}}}}}}}}=\frac{1}{2}\left(1-\parallel q{\rho }_{+}^{\otimes M}-(1-q){\rho }_{-}^{\otimes M}\parallel \right)\ ,$$
(3)

where Pe,Col denotes the error probability which can be attained by collective measurements and ∥A∥ is the sum of the absolute values of the eigenvalues of A. It is known that the Helstrom bound can be saturated by measuring the following observable, which may or may not correspond to a collective measurement

$${{\Gamma }}=q{\rho }_{+}^{\otimes M}-(1-q){\rho }_{-}^{\otimes M}\ .$$
(4)

The state ρ± is guessed according to the sign of the measurement output. Note that, in some scenarios, Γ will be either positive or negative meaning that the best strategy is always simply to guess the corresponding state. In practice, we implement the operator Γ, through a positive operator valued measure (POVM). A POVM is a set of positive operators {Πk ≥ 0}, which sum to the identity \({\sum }_{k}{{{\Pi }}}_{k}={\mathbb{I}}\). In general, to experimentally implement an arbitrary POVM, Naimark’s theorem46 is used to convert the POVM to a projective measurement in a higher dimensional Hilbert space. However, it transpires that for the purposes of this work, the number of POVM elements necessary to saturate Helstrom’s bound is less than or equal to the dimensions of the Hilbert space and so Naimark’s theorem is not needed. Using the optimal measurement, given in Eq. (4), and the definition of error probability in Eq. (2), we can verify that the Helstrom bound becomes (1 − ∥Γ∥)/2, as expected from Eq. (3)47. In general, the POVM required to implement Γ will correspond to a collective measurement. In this work we implement two-copy collective measurements, as depicted in Fig. 1b).

Optimal separable measurement

A separable measurement is any measurement where entangling operations are not allowed, i.e. only LOCC are allowed. Although there are many different types of LOCC measurements11, for the purposes of this work, we need only consider the optimal separable measurement. In general, this requires measurements that are optimised depending on the number of copies available. When finding the optimal LOCC measurement for a large number of copies, it can be beneficial to use a dynamic programming approach23. As we are concerned with LOCC measurements on only a small number of copies of the state it is easy to verify the optimal measurement by a brute force computation. A description of the simulation approaches used to find the optimal LOCC measurements is provided in the methods section.

For the scenario we are considering, the individual measurements are parametrised by a single angle. We need only consider the measurements defined by the projectors \({{{\Pi }}}_{0}=\left\vert \psi \right\rangle \left\langle \psi \right\vert\) and \({{{\Pi }}}_{1}=\left\vert {\psi }^{\perp }\right\rangle \left\langle {\psi }^{\perp }\right\vert\) where

$$\left\vert \psi \right\rangle =\cos (\phi )\left\vert 0\right\rangle +\sin (\phi )\left\vert 1\right\rangle \ ,$$
(5)

and \(\left\langle \psi \right\vert \left\vert {\psi }^{\perp }\right\rangle =0\). For two-copy LOCC measurements the optimal angle used in the second measurement will depend on the measurement outcome of the first POVM as shown in Fig. 1a). Either Π0 or Π1 will click in the first measurement, giving two different posterior probabilities, which will each have their own optimal measurement angle. After the second measurement the posterior probabilities are updated again and the more likely state is chosen as our guess. Therefore, the optimal two-copy LOCC measurement is described by three measurement angles, which can be numerically optimised to find the minimum expected LOCC error probability.

Gap between collective and separable measurements

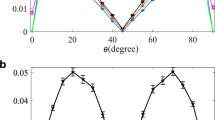
Knowledge of the optimal separable and collective two-copy measurements enables us to find an experimentally feasible regime for demonstrating the advantage of collective measurements. This is done by operating in the regime of unequal priors, i.e. q ≠ 0.5. This operating regime was found through the rather surprising observation that at q = 0.5, for two copies, LOCC measurements perform the same as collective measurements but for three copies collective measurements outperform LOCC measurements. The expected error probabilities for both collective and LOCC measurements for distinguishing two copies and three copies of the quantum state are shown in Fig. 2a). To investigate this behaviour further, we define the gap between LOCC measurements and collective measurements for M copies of the quantum state (in terms of minimum attainable error probability), as

$${{{\Delta }}}_{M}={P}_{{{{{{{{\rm{e}}}}}}}},{{{{{{{\rm{LOCC}}}}}}}}}(M)-{P}_{{{{{{{{\rm{e,Col}}}}}}}}}(M)\ ,$$
(6)

where Pe,LOCC(M) corresponds to the minimum error probability which can be attained with LOCC measurements given M copies of the unknown state, \({\rho }_{\pm }^{\otimes M}\). We plot this quantity in Fig. 2b) for a particular value of α and v. Further plots of Δ for different sets of α and v values are presented in Supplementary Note 1. The optimal LOCC measurement is obtained using dynamic programming, with 2501 entries in the measurement angle and error probability tables. The number of entries in these tables corresponds to how discretised the space of possible measurement angles is. A greater number of entries therefore corresponds to greater numerical accuracy. 2501 entries was found to be a sufficiently large number of entries to ensure the optimality of our solutions to 9 significant figures. Although, the differences between two and three-copy measurements in Fig. 2 are interesting in and of itself, the key take-away here is that two-copy collective measurements can offer an advantage over LOCC measurements when q ≠ 0.5. This is important as two-copy collective measurements are at the limit of what is experimentally feasible30.

Fig. 2: Experimentally feasible regime for demonstrating state discrimination enhanced by collective measurements.
figure 2

a The expected error probabilities attainable for distinguishing between two and three copies of the quantum state, \({\rho }_{\pm }^{\otimes 2}\) and \({\rho }_{\pm }^{\otimes 3}\), when allowing only local operations and classical communication (LOCC) measurements (Pe,LOCC) and when allowing collective measurements (Pe,Col). b We plot the gap between the optimal LOCC measurement and the optimal collective measurement for two and three copies of the probe state. These plots correspond to α = π/4 and v = 0.1. In both figures the solid and dashed lines correspond to two- and three-copy results respectively.

Full size image

Experimental Results

Two-copy collective measurement results

It is always possible to saturate the Helstrom bound by implementing the observable given in Eq. (4). However, mapping this observable to an experimental set-up is not straightforward. To circumvent this, we numerically find a projective measurement that saturates the Helstrom bound. From this, the unitary matrix we need to implement can be obtained30. Finally, we convert the necessary unitary matrix to experimentally implementable quantum circuits using a known decomposition37. This involves finding 15 free parameters and requires only three CNOT gates as is shown in Fig. 1c). We then implement these circuits on the F-IBM QS1 processor. When measuring in the computational basis there are four possible measurement outcomes, \(\left\vert 00\right\rangle ,\left\vert 01\right\rangle ,\left\vert 10\right\rangle\) and \(\left\vert 11\right\rangle\).

We assign the outcome \(\left\vert 00\right\rangle\) to the state ρ− and the remaining outcomes are assigned to the state ρ+, i.e. if the circuit output is \(\left\vert 00\right\rangle\) we guess that the unknown state was ρ−, for all other measurement results we guess ρ+. By preparing the states ρ+ and ρ− many times, the average error probability can be extracted. We repeat this for several different prior probabilities using an optimised POVM for each prior. For each prior probability, we use 200,000 shots, to ensure we obtain an accurate estimate of the average error probability. The results of these experiments are shown in Fig. 3 for three different sets of α and v values. The red shaded regions in Fig. 3 correspond to the minimal error probability which can be achieved by any LOCC measurement. The blue shaded regions correspond to the error probability which can be attained by the optimal collective measurements. In theory, our quantum circuits should be able to reach the minimum error probability set by the blue line. However, as can be seen in Fig. 3 our experiment does not reach the theoretical collective measurement limit. This is due to a combination of gate errors and readout error in the F-IBM QS1 device. Nevertheless, in several instances our collective measurements surpass what is possible by LOCC measurements. For example, the two data points shown in the inset of Fig. 3 surpass the expected error probability attainable by LOCC measurements by more than six standard deviations. To the best of our knowledge, this is the first time this has been achieved for quantum state discrimination.

Fig. 3: Experimental data for discriminating quantum states using two-copy collective measurements.
figure 3

In all three figures the shaded red region corresponds to the error probabilities accessible by local operations and classical communication (LOCC) measurements and the blue region corresponds to the error probabilities attainable by collective measurement. The blue markers correspond to the experimental data. Each data point corresponds to 200,000 shots. All data points include statistical error bars corresponding to one standard deviation obtained via bootstrapping, but in most cases the data points are larger than the error bars. The inset is included in the first figure to show the scale of the error bars. Each data point corresponds to a measurement optimised for that particular prior probability.

Full size image

However, we note that not all of our experiments were successful in showing the advantage of collective measurements. For some values of α and v, our collective measurements achieved an error probability that was comparable to the best LOCC measurement. These data points are included in Supplementary Note 2.

Simulation of two-copy collective measurement with noise

We now present a noisy simulation of one particular implementation of our two-copy collective measurement to provide an indication of the noise level needed to reach the Helstrom bound in future experiments. We use IBM Q’s QISKIT package to model the noise, which includes readout error and depolarising noise on all gates. We choose a starting noise level that approximates the device used in our experiments: single qubit gate error rates of 10−3, two qubit gate error rates of 10−2, \(\left\vert 0\right\rangle\) state readout error of 10−2 and \(\left\vert 1\right\rangle\) state readout error of 2 × 10−2. With these parameters, we model the error probability which can be attained for v = 0.1, α = π/4 and q = 0.75. The simulation was then repeated, scaling all the error rates by a noise scaling term, as shown in Fig. 4. As expected, when the noise is scaled down sufficiently, the two-copy collective measurement approaches the Helstrom bound. These simulations suggest that an improvement in error rates by approximately one order of magnitude would allow the two-copy Helstrom bound to be saturated. However, this comes with the caveat that the noise model used may be missing important features.

Fig. 4: Simulation of two-copy collective measurement with noise.
figure 4

The error probability is shown as a function of the noise scaling term, with the default noise parameters, corresponding to a scaling of 1, specified in the Simulation of two-copy collective measurement with noise section. The two states being discriminated are characterised by v = 0.1, α = π/4 and q = 0.75. The shaded red and blue regions correspond to the limits of local operations and classical communication (LOCC) and collective measurements respectively. The black cross corresponds to the experimentally obtained error probability based on 200,000 shots, and the statistical error bars based on bootstrapping are smaller than the marker size. The horizontal positioning of the experimental data point is of no physical significance. The dashed black vertical line corresponds to a noise scaling of 0.6.

Full size image

Three- and four-copy collective measurements

Finally, we extend the above results to three- and four-copy collective measurements. The three- and four-copy measurements that we implement were found by searching for projective measurements in a three and four-qubit Hilbert space respectively. In the ideal case, the three-copy measurement found is able to saturate the three-copy Helstrom bound. The four-copy measurement cannot saturate the four-copy Helstrom bound, however, it can surpass the optimal four-copy LOCC measurement. To saturate the four-copy Helstrom bound with projective measurements would likely require ancilla qubits, which would significantly increase the complexity of the corresponding quantum circuit. For v = 0.1, α = π/4 and q = 0.75, we implemented these three- and four-copy measurements on the F-IBM QS1 device, with the results presented in Fig. 5. Notably, both the three- and four-copy measurement perform worse than measuring only a single qubit. This suggests that when given many copies of a state, rather than trying to implement a very complex entangling measurement, it is better to measure the quantum states in smaller groups. Even in an optimistic scenario, we will need an order of magnitude reduction in noise levels for the four-copy entangling measurement to be useful. However, it should be noted that if it was known in advance that our measurement device is extremely noisy, we can always attain an error probability of 0.25 as, in this case, we can simply ignore our measurement results and guess the more likely state.

Fig. 5: Three- and four-copy collective measurements - experiments and simulation.
figure 5

The error probability is shown as a function of the noise scaling term, with the default noise parameters, corresponding to a scaling of 1, specified in the Simulation of two-copy collective measurement with noise section. The two states being discriminated are characterised by v = 0.1, α = π/4 and q = 0.75. The crosses correspond to the experimentally obtained error probabilities based on 200,000 shots, and the statistical error bars based on bootstrapping are smaller than the marker size. The horitzontal positioning of the experimental data points is of no physical significance. The solid horizontal lines show the theoretical limit given by the Helstrom bound for the corresponding number of copies (Pe,Col(ρ⊗M)).

Full size image

In contrast to the three-copy experimental results, the simulation of the three-copy measurement, using the same noise parameters as the previous section, performed quite well. This highlights the limitations of our noise model, particularly for circuits involving larger numbers of qubits. For example, qubit connectivity becomes an important factor in practical three-copy measurements. There is also a significant gap between the experimental results and the noisy simulation in the four-copy case. These experiments and simulations suggest that while it is possible to surpass the LOCC limits using two-copy collective measurements, the ultimate limits in state discrimination shall remain out of reach for the foreseeable future.

Conclusion

Recent experimental advances have led to collective measurements offering an advantage in several areas of quantum information28,29,30,48,49,50,51. However, prior to this work, this advantage had not been extended to quantum state discrimination. By utilising the F-IBM QS1 superconducting processor and operating in the regime of unequal prior probabilities, we have been able to experimentally distinguish two copies of two quantum states with an error probability smaller than the best possible LOCC measurement. The further development of this capability may aid numerous applications of quantum state discrimination, including quantum illumination52,53,54,55 and exoplanet detection56.

There are several natural avenues for extending this work. In this work, we have taken, as our figure of merit, the average error in distinguishing two states, but several other figures of merit are commonly used57,58, including unambiguous state discrimination59,60, asymmetric state discrimination61 and state discrimination using the minimum number of copies62. When decomposing the three- and four-copy measurement circuits, we simply used the default decomposition provided on QISKIT. It may be possible to obtain an approximate circuit with a similar theoretical minimum error probability, but requiring a greatly reduced number of CNOT gates63. Furthermore, this work may be extended to examine the role of collective measurements when distinguishing more than two states64 or for distinguishing states which live in a larger Hilbert space, as has been done for two qubit states65. In this work, we have experimentally investigated the role of collective measurements for only a small number of copies of the quantum state. However, going beyond the few-copy setting and investigating the asymptotic attainability of the ultimate limits in quantum state discrimination, as has recently been done in quantum metrology66, may reveal other important features of state discrimination.

Note added: While this manuscript was under review we became aware of new work where two-copy collective measurements were used for minimum consumption state discrimination67.

Methods

Details of numerical simulations for finding the optimal LOCC measurement

Here we give a detailed description of how the expected error probabilities attainable by LOCC measurements are computed. We first describe the dynamic programming approach used in previous works10,11,23. This technique allows us to break the overall optimisation problem into smaller optimisation problems which can be solved in turn. We wish to find the measurement angles which minimise the expected probability of error when allowing LOCC measurements on multiple copies of the state ρ.

We define qi as the probability that the unknown state is the state ρ+ just before performing the ith measurement. Hence, the initial prior probability that the unknown state is ρ+, which is denoted q in the main text, is denoted q1 in this section. After performing each measurement, the posterior probability of the unknown state being ρ+ will change, depending on the measurement result. At each stage, we wish to find the optimal angle ϕ for the measurement given by Eq. (5). The optimal angle for the ith measurement, ϕi, is that which minimises the average error probability and will depend on the number of copies available M and the prior probability qi. For every measurement there are two possible outcomes, \({{{\Pi }}}_{0}(\phi )=\left\vert \psi \right\rangle \left\langle \psi \right\vert\) or \({{{\Pi }}}_{1}(\phi )=\left\vert {\psi }^{\perp }\right\rangle \left\langle {\psi }^{\perp }\right\vert\), where we have made the dependence on ϕ explicit. The probability of each outcome is given by \({{{{{{{\rm{tr}}}}}}}}\{\rho {{{\Pi }}}_{i}\}\). We shall denote the outcome of the ith measurement as Di, so that Di can correspond to either Π0 or Π1 clicking. Given the measurement outcome Di, the posterior probability after performing the ith measurement (or equivalently the prior probability for the following measurement) is given by

$${q}_{i+1}=\frac{\Pr \left[{D}_{i}| {\rho }_{+},{\phi }_{i}\right]{q}_{i}}{\Pr \left[{D}_{i}| {q}_{i},{\phi }_{i}\right]}\ ,$$
(7)

where Pr[Di∣a] is the probability of observing the measurement outcome Di given the conditions a.

Given M total states to measure, we can measure m (m ≤ M) states to obtain an intermediate error probability. We denote the expected error probability (with M − m states available to measure) as Rm. Using this notation, RM is the error probability when there are no states left to measure. At this point, the optimal strategy is simply to guess whichever state is more likely, so that

$${R}_{M}=\min ({q}_{M+1},1-{q}_{M+1})\ .$$
(8)

Note that at each measurement stage Rm depends on qm+1, which is determined by the preceding measurement angles ϕ1, ϕ2(D1), ϕ3(D1, D2)…ϕM(D1, D2, . . , DM−1). The expected error probability at each previous measurement step can be calculated from the error probability at the current step

$${R}_{m-1}({q}_{m})=\mathop{\sum}\limits_{{D}_{m}}\Pr [{D}_{m}| {q}_{m},{\phi }_{m}]{R}_{m}({q}_{m+1})\ .$$
(9)

Our aim is to minimise the expected error probability when all M copies of the quantum state are available to measure, denoted R0. If we have only a single copy of the quantum state left to measure, the optimal measurement angle is known to be11

$${\phi }_{M,{{{{{{{\rm{opt}}}}}}}}}({q}_{M})=\frac{1}{2}{{{{{{{\rm{arccot}}}}}}}}((2{q}_{M}-1)\cot (\alpha ))\ .$$
(10)

This allows RM−1 to be calculated. RM−2 can then be calculated by minimising Eq. (9). Each measurement stage can be recursively optimised in this manner. Continuing in this manner gives R0(q1) as the expected error probability.

Dynamic programming offers an efficient way to compute the optimal angles. In the two-copy case it is possible to do a brute force search for the optimal angles to verify the correctness of our simulations. A simple expression for the expected error probability in the two-copy case is given by

$${R}_{0}({q}_{1})=\, {p}_{0}^{1}{p}_{0| 0}^{2,1}{R}_{2}({q}_{2| 00})+{p}_{0}^{1}{p}_{1| 0}^{2,1}{R}_{2}({q}_{2| 01})\\ +{p}_{1}^{1}{p}_{0| 1}^{2,1}{R}_{2}({q}_{2| 10})+{p}_{1}^{1}{p}_{1| 1}^{2,1}{R}_{2}({q}_{2| 11})\ ,$$
(11)

where \({p}_{i}^{1}\) is the probability of the POVM Πi clicking, \({p}_{i| j}^{2,1}\) is the probability of the POVM Πi clicking in the second measurement given that the POVM Πj clicked in the first measurement and q2∣ij is the posterior probability when Πi clicked in the first measurement and Πj clicked in the second measurement. By numerically searching over all angles we can verify the correctness of our results in the two-copy case. However, even in the three-copy case a numerical search is already very slow compared to dynamic programming.

Finally, we note that in Figs. 2 and 3 we can observe points where the gradient of the LOCC error probability is not continuous. It is worth noting that the discrete nature of Eq. (8) is responsible for this behaviour.