Introduction

Nuclear electron interactions induce particularly small splitting in atomic energy levels, defined as hyperfine structure. Spectroscopically investigating hyperfine structures reveals highly valuable information related to nuclear properties and atomic structures1. Extension of the spectroscopic target, from the usually studied neutral atoms or singly charged ions to highly charged ions (HCIs), represents an excellent approach to enhance hyperfine interactions owing to contracted electron clouds. Spectroscopic measurements of hyperfine structures in few-electron HCIs, such as H-, He-, Li-, and Be-like ions, have been widely performed by taking advantage of their large hyperfine splittings. They have successfully contributed to tests of relativistic and quantum electrodynamics (QED) atomic theories as well as investigations of nuclear properties2,3,4,5,6,7,8,9,10,11,12,13,14.

In contrast to few-electron HCIs, hyperfine spectroscopy of many-electron HCIs provides distinctive examples to gain a deeper understanding about complex relativistic electron correlations. Nevertheless, this implicates considerable experimental challenges as high spectral resolution (i.e., better than their slightly enhanced hyperfine structure) is required. Such HCIs have recently attracted much attention, triggered by proposals for their application in high-precision atomic clocks. HCI clocks are expected to be a sensitive probe for time variations of the fine-structure constant α for testing modern physical theories beyond the Standard Model15. A number of candidates for HCI clocks have been proposed16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31, and their transition wavelengths have been experimentally investigated32,33,34,35. Micke et al. recently demonstrated quantum logic spectroscopy of HCIs using Ar13+, which has no hyperfine structure, promising realization of the HCI clocks36,37. For further HCI atomic clock development employing fascinated transitions highly sensitive to the α variation15, it is necessary to gain a better understanding of hyperfine structure in many-electron heavy HCIs with a nuclear spin. The atomic-structure calculations have been developed to provide hyperfine-structure constants38,39,40,41,42, and several theoretical studies suggested that hyperfine interactions in promising HCI clock candidates substantially affect their clock operation and attainable uncertainties16,26,27,31,33. Although the lifetime measurement studying hyperfine interaction in many-electron HCIs has already been reported43, spectroscopic measurements of hyperfine-structure constants in many-electron HCIs have not proceeded.

Here, we study the hyperfine structures in the 4d95s metastable states of Pd-like 127I7+ using laser-induced fluorescence (LIF) spectroscopy. Historically, LIF spectroscopy of trapped HCIs free from systematic Doppler shifts was pioneered by Hosaka et al.44. They demonstrated a CW-laser-induced fluorescence spectroscopy of the electric-dipole (E1)-allowed transition 2s-2p3/2 of H-like ions in an electron beam ion trap (EBIT) plasma by monitoring the enhancement of the Lyman-α emission45. In the past decade, resonant laser spectroscopy (RLS) of forbidden transitions using a combination of pulsed laser and time-resolved fluorescence detection has investigated the simple doublet fine-structure splittings in Ar13+ (see ref. 46) and Fe13+ (see ref. 47) under a strong magnetic field without an electron beam. In this paper, we demonstrate time-resolved LIF spectroscopy of HCIs in an EBIT using E1-forbidden transitions both for laser excitation and fluorescence detection. High-resolution spectroscopy of the transition between highly excited metastable states is achieved with the aid of excitation processes in the EBIT plasma. A similar experimental scheme was proposed for 3d94s in Ni-like HCIs48; however, this has not yet been demonstrated. It is worth emphasizing that we operate the EBIT with a low magnetic field condition to suppress the Zeeman splitting and employ the evaporative cooling technique for reduction of the Doppler line broadening, leading to clear observation of the hyperfine splitting.

Results

Concept of the plasma-assisted laser spectroscopy

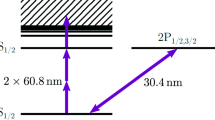
In the present experiment, we prepare the (4\({d}_{5/2}^{9}5s\))J=3 metastable state of 127I7+ in an EBIT and irradiate the trapped HCI with a pulsed laser, as shown in Fig. 1a. Figure 1b shows the experimental scheme used with the level structure of 127I7+. Due to the closed 4d10 shell structure in the ground state, the excitation energy to the first excited fine-structure level (4\({d}_{5/2}^{9}5s\))J=3 is relatively high at ~47 eV. Although such high-energy states are generally de-excited in a short time, the lifetimes for every hyperfine level in (4\({d}_{5/2}^{9}5s\))J=3 are longer than 10 s because their de-excitation processes are strongly forbidden, except for M3 and hyperfine-mixing E2 transitions. From the long-lived fine-structure level, the extreme ultraviolet (EUV) electric-quadrupole (E2) transition ((4\({d}_{3/2}^{9}5s\))J=2 → (4d10)J=0) was induced by pulsed laser excitation via the M1 transition ((4\({d}_{5/2}^{9}5s\))J=3 → (4\({d}_{3/2}^{9}5s\))J=2). Both the initial and excited levels in the laser excitation are metastable states without any E1 decay path; thus, the natural width of the transitions is estimated to be ~10−5 cm−1 (1 cm−1 = 2.99792 × 1010 Hz) from the theoretical 4 μs lifetime of the upper fine-structure level (4\({d}_{3/2}^{9}5s\))J=2. The intrinsically narrow natural width of the laser transitions contributes to the high resolution in spectroscopic measurements, revealing the hyperfine structure.

Fig. 1: Schematic diagram of the present laser spectroscopy.
figure 1

a Brief overview of the present laser-induced fluorescence (LIF) spectroscopy with the schematic trap region and ions. b Experimental scheme with the energy diagram of 127I7+. The population rate of (4\({d}_{5/2}^{9}5s\))J=3 (1/τpopulation) was estimated, using collisional-radiative modeling49. τcol, τE2, and τlaser are depopulation lifetimes by electron collision, electric-quadrupole (E2) radiative decay, and laser-induced magnetic-dipole (M1) excitation, respectively. An electron energy of 105 eV and a density of 1010 cm−3 are assumed in the collisional-radiative rates, corresponding to the present experimental condition. The energy structure and lifetime were calculated using GRASP201841.

Full size image

The long-lived state (4\({d}_{5/2}^{9}5s\))J=3 of 127I7+ was continuously prepared through collisional and radiative processes in the EBIT plasma. Although increasing the number of trapped ions necessitates an enhanced electron density of the plasma, electron collisions must be suppressed to detect LIF emissions from the laser-excited fine-structure level with a lifetime in the order of microseconds. We controllably maintained the EBIT electron density below 1010 cm−3, where the total collisional excitation and de-excitation rate out of the (4\({d}_{3/2}^{9}5s\))J=2 level was approximately 103 s−1(see ref. 49). The production rate of (4\({d}_{5/2}^{9}5s\))J=3 under an electron density of 1010 cm−3 was estimated to be ~160 s−1 from collisional-radiative modeling49. Thus, the excitation rate by the pulsed laser was operated at less than 1 s−1 to avoid depletion of the population in the initial state (4\({d}_{5/2}^{9}5s\))J=3. This well-designed closed transition cycle, including the plasma processes, maintains the sequential LIF detection, suppressing the unintended population loss for the initial and excited levels in the laser excitation. We emphasize that the well-defined laboratory plasma and its control along with a deep understanding of the excitation and de-excitation dynamics through collisional-radiative modeling allow us the LIF detection, even though the ions are in plasma.

The hyperfine splitting for each fine-structure level is given by the magnetic-dipole hyperfine-structure constant Ahfs, the electric-quadrupole hyperfine-structure constant Bhfs, and the quantum numbers J, F, and I. Ahfs and Bhfs are relevant values to the atomic structure and the nuclear moments. The nuclear properties of 127I, the only stable isotope of iodine, have been well investigated50: nuclear spin I = 5/2, nuclear magnetic moment μI = 2.81327(8)μN and nuclear electric-quadrupole moment QI = 0.689(15) b. We calculated the hyperfine-structure constants and splittings for (4\({d}_{5/2}^{9}5s\))J=3 and (4\({d}_{3/2}^{9}5s\))J=2 using the atomic calculation code GRASP201841 as shown in Fig. 1b. In general, a contracted electron orbital in HCIs enhances the hyperfine splitting. In addition, in the present atomic system, the 5s electron orbital in the HCI has a significant overlap with the nucleus, resulting in large hyperfine splitting. In fact, our theoretical calculation shows that the Ahfs constant for (4\({d}_{5/2}^{9}5s\))J=3 in 127I7+ is six times larger than that for 4\({d}_{5/2}^{9}\) in 127I8+, even though the binding energy is smaller.

Prediction of the spectral profile

The hyperfine structures split the laser transition into 14 components, considering the selection rules for M1 transitions (ΔF = ±1, 0). Spectral simulations were performed to predict the features of the laser excitation spectrum, including hyperfine structures. Figure 2a shows the statistical weight of the initial state with the wavenumber deviation Δk corresponding to the difference from the original transition energy without the hyperfine structures. Figure 2b shows the spectral intensity gA, which is the sum of Einstein A coefficients of the ΔmF = 0 transitions for every magnetic sub-level. We also calculated the Zeeman splitting using the intermediate magnetic field treatment, as shown in Fig. 2c. Equations and atomic codes are summarized in “Methods”. According to the simulation, the M1 transition lines are distributed over several cm−1, and the spectral features under low magnetic field conditions have an asymmetric profile because of their specific quantum numbers and the intrinsic difference in the Racah coefficients between these transitions. At high magnetic fields above 0.5 T, such as that in a typical EBIT, magnetic sub-level-resolved transitions spread over a wide Δk range, which hinders the experimental assignment of hyperfine components. To overcome this difficulty, we employed the low magnetic field operation (0.03 T) of a compact electron beam ion trap (CoBIT)51 at the University of Electro-Communications. Although this magnetic field is not classified as the weak-field limit, it is sufficiently low enough to suppress the Zeeman splitting below 0.05 cm−1. The asymmetries of these splittings are less than 0.01 cm−1. This quasi-Zeeman-free condition enables us to resolve the hyperfine structures.

Fig. 2: Theoretical predictions for the hyperfine-structure splitting in the laser excitation.
figure 2

a Statistical weights of the initial state (4\({d}_{5/2}^{9}5s\))J=3. b Spectral intensity (gA). c Zeeman splitting. Solid and dotted lines show the ΔmF = 0 and ΔmF = ±1 transitions, respectively. The red line represents the present experimental condition. The typical magnetic field in an electron beam ion trap (EBIT) is shown by the purple shade. d Doppler broadening simulation. The transition energy was taken from the NIST database55.

Full size image

In the present experiment, line broadening is expected to be dominated by the Doppler effect due to ion motion in the EBIT, since the Zeeman splitting, laser linewidth, and natural width of the transition are all less than 0.05 cm−1. Figure 2d shows the spectral broadening simulation under the assumption of a Maxwellian distribution for the kinetic energies of the trapped ions in the EBIT52. In the low-temperature region, the width of each transition line becomes narrow, and the associated features originating from the F = 7/2 → \({F}^{{\prime} }=7/2\) and F = 9/2 → \({F}^{{\prime} }=9/2\) transitions appear around 17,631–17,632 cm−1. The simulation shows that the ions should be cooled below 20 eV to characterize the hyperfine structures and determine the spectroscopic parameters.

Measurement of the laser-induced fluorescence

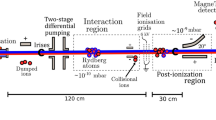
Figure 3a shows the present experimental setup. From CH3I vapor, 127I7+ ions were produced by an electron beam and stored in an electrostatic trap potential formed by the electron beam and three successive cylindrical drift-tube (DT) electrodes49. To efficiently produce 127I7+ ions, the electron beam energy (105 eV) and current (2 mA) were experimentally determined by monitoring the emission intensity of the E2 transition (4\({d}_{3/2}^{9}5s\))J=2 → (4d10)J=049. To excite the M1 transitions, we used a wavelength-tunable dye laser (Sirah Cobra-Stretch with the dual 3000 lines/mm grating option, Exciton Rhodamine 6G/ Ethanol dye solution, 567 nm) pumped by the second harmonic of an Nd:YAG nanosecond-pulsed laser (Cutting Edge Optics Gigashot, 10 ns) with a 100 Hz repetition rate. The wavelength of the laser was monitored using a high-precision wavemeter (High Finesse, WS-6-600). The laser pulse energy was tuned and maintained at ~7 mJ/pulse by the combination of a λ/2 wave plate and polarizer. The polarization of the laser was perpendicular to the magnetic field so that only the ΔmF = 0 transitions were excited. LIF was monitored with a time-resolving extreme ultraviolet (EUV) spectrometer consisting of an aberration-corrected concave grating (Hitachi 001-0660) and a position-sensitive detector (PSD, Quantar Technology Inc., model 3391)53. A typical 127I7+ emission spectrum obtained with the EUV spectrometer is shown in Fig. 3b. Owing to the large difference in wavelength, the LIF signal can be readily distinguished from the laser-scattering noise. The prominent line at 49 eV is the targeted E2 transition ((4\({d}_{3/2}^{9}5s\))J=2 → (4d10)J=0), which was used to detect laser excitation. To distinguish the LIF signal from the continuous emission induced by collisional and radiative processes in the plasma, the time spectrum of the E2 transition was recorded with a Multi-Channel-Scaler (MCS) as shown in Fig. 3c. The observed lifetime of the LIF signal was ~4 μs, which agrees with our theoretical calculation.

Fig. 3: Overview of the LIF detection setup.
figure 3

a Schematic of the experimental setup consisting of the electron beam ion trap (EBIT) with a time-resolved laser-induced fluorescence (LIF) detection system. FG, DG, MCS, and PSD represent a Function Generator, Delay Generator, Multi-Channel-Scaler, and Position-Sensitive detector, respectively. b Typical EUV emission spectrum. c Time-resolved signal for the laser-induced E2 transition fluorescence.

Full size image

LIF spectrum and its analysis

Figure 4 shows the laser wavelength spectrum of the LIF signal. It took a few hours to accumulate LIF counts at each wavelength. To compensate for possible fluctuation in the number of stored ions, the LIF counts were normalized by continuous E2 counts, which are regarded to be proportional to the ion number. The vertical axis in Fig. 4 represents the ratio of LIF signal counts within 10 μs after laser irradiation to the total counts, including the continuous emission within the interval of laser irradiation (10 ms). The background level due to continuous plasma emission in the ratio was directly determined to be 0.001 from the time range ratio (10 μs/10 ms). In a preliminary scan, a broad main structure at 17,633–17,634 cm−1 and associated structures at 17,634–17,636 cm−1 were observed. We considered that the associated structures were important for understanding the origin of the spectral features. Therefore, a finer wavelength scan of this region was performed to obtain higher statistics, as shown in Fig. 4. In the fine scan, all DT electrodes were set to ground potential to suppress the Doppler line broadening. While the axial potential formed by the electron beam still enables the storage of 127I7+ ions, the resulting shallow axial potential allows for evaporative cooling, yielding a reduction in the spectral linewidth52,54. Comparing results to the spectral simulation, we conclude that the main and associated features are primarily composed of ΔF = –1 and 0 transitions, respectively.

Fig. 4: Experimental LIF spectrum.
figure 4

The fitting result (black line) is shown with separated profiles (blue, green, and orange lines) for every transition. The error bar for each experimental data point (red diamond) represents the statistical error.

Full size image

To determine the hyperfine-structure constants, the observed spectrum was fitted with a model function incorporating all hyperfine-resolved transitions with the same Doppler width kD. The model function is described in “Methods”. The center of the transition energy for each line is determined by the original transition energy k0 for the fine-structure transition and the hyperfine-structure constants for each of the initial and excited fine-structure levels. The relative line intensity for each transition was defined by the simulation intensity in Fig. 2b. Consequently, the seven parameters Ahfs, Bhfs, \({A}_{hfs}^{{\prime} }\), \({B}_{hfs}^{{\prime} }\), k0, kD, and total spectral intensity I0 were determined in the fitting procedure, where the primed quantities refer to the excited fine-structure level. Note that theoretically calculated Einstein A coefficients were used to determine the simulated intensities. The intensity model mainly depends on the Racah coefficients, whereas the actual intensity is slightly different because of the hyperfine mixing with other fine-structure levels. We theoretically evaluated the hyperfine-mixing effect on the transition intensities and found that this contribution is less than 0.05 s−1 for every Einstein A coefficient. This uncertainty in the model function affects the determination of the experimental values by less than 1 % of the experimental uncertainty and is thus considered insignificant. The statistical population in the intensity model may also be disturbed by the lifetime difference between hyperfine levels43. However, in the case of 127I7+, it is not necessary to consider such possibilities because the radiative decay rates are at least 103 times longer than the collisional-radiative rate supplying the population to the metastable fine-structure level; hence, the populations are not quenched by spontaneous decay to the ground state. Thus, we consider the intensity model used here to be reasonable for determining the constants. The fitted profiles for each hyperfine component and their convolution are shown in Fig. 4. The obtained parameters are listed in Table 1 along with the theoretical values calculated by the GRASP code taking the Breit and quantum electrodynamic (QED) effects into account. The reduced-chi-square in the fitting was 1.1. From the laser wavelength stability during the measurement, the systematical errors for the hyperfine-structure constants were estimated to be 0.3 GHz. The systematic error of k0 is 0.03 cm−1 taking the absolute accuracy of the wavemeter into account. The resulting kD is 0.46 (±0.04) cm−1 corresponding to an ion temperature of 15 (±2) eV under the assumption that Doppler broadening dominates in the spectral linewidth. The shallow trapping potential formed by the zero DT voltage and the thin electron density with a low magnetic field enabled the trapped ions to be evaporatively cooled down to temperatures similar to those found in forced evaporative cooling by turning off the electron beam46. The narrow Doppler width realized in the present measurement is essentially important for resolving the hyperfine splitting.

Table 1 Summary of the experimental and theoretical values for (4\({d}_{5/2}^{9}5s\))J=3 and (4\({d}_{3/2}^{9}5s\))J=2 in 127I7+.
Full size table

Because the nuclear spin and moments of 127I are well-known50, the experimentally obtained hyperfine-structure constants are used to validate the theoretical calculation of the electron orbital for each fine-structure level. Experimental results obtained here show reasonable agreement with theoretical values, considering the uncertainties. The transition energy k0 obtained by the experiment agrees with the theoretical calculation within ~0.1%. The Breit interaction shifts the transition energy by 2%, which is important to reproduce the experimental result. The energy of each fine-structure level has been compiled in the NIST database55 from several experimental results using passive spectroscopy, and the uncertainty was evaluated to be 100 cm−1. In the present study, we clearly demonstrate that our active spectroscopic approach succeeded in directly measuring the transition energy and greatly reducing its uncertainty. This clarified the importance of the relativistic configuration-interaction (RCI) correction for the Breit interaction.

Discussion

We have demonstrated laser spectroscopy of forbidden transitions between metastable states of HCIs stored in an EBIT by employing Pd-like 127I7+. The laser excitation spectrum of the HCIs in a quasi-Zeeman-free low magnetic field revealed distinct hyperfine structures, which provided evidence for the enhancement of the hyperfine interaction via a contracted electron cloud with a 5s valence electron. The resulting hyperfine-structure constants of highly charged ions with a well-known nucleus provide a benchmark for atomic orbital calculations with relativistic many-electron correlations, allowing for discussion of the electron cloud in the vicinity of the nucleus for each fine-structure level. Even though the transition observed in this study is not a proposed HCI clock candidate, the building of a benchmark to understand hyperfine structures in many-electron HCIs makes a significant step toward developing such clocks, considering especially that the currently most promising clock candidates with a 5s-4f level crossing15,16,17,18,20,23,24,25,26,27,28,32 are intrinsically accompanied by a similar characteristic electron configuration having a single 5s electron. The established benchmarks would serve as a reference to enhance the understanding of the hyperfine interaction in many-electron HCIs.

The present hyperfine-structure-resolved laser spectroscopy offers future possibilities for experimental studies in nuclear physics using HCIs, such as a broad investigation of unknown nuclear spins and moments and hyperfine anomalies with a specialized EBIT for highly charged radionuclide ions56. Recently, high-precision atomic orbital calculations have been extensively developed to investigate nuclear properties from hyperfine-structure constants57,58,59,60,61. While this approach had the privilege for particular nuclei with optically accessible transitions at low valence ions, the extension of the target to HCIs enables the selection of an atomic-level structure by changing the charge state. In addition, an ns-valence state enhancing its hyperfine interaction can be arbitrarily selected, in contrast to neutral atoms or singly charged ions whose electron configurations are fixed. We consider that the present LIF scheme has the potential to be a versatile method for investigating heavy nuclear properties because it can be directly applied to the three transitions in Pd-like ions and Ni-like ions, as follows. Pd-like ions have an additional excitation pathway from the long-lived (4\({d}_{5/2}^{9}5s\))J=3 state to the (4\({d}_{5/2}^{9}5s\))J=2 excited fine-structure level via an M1-allowed transition. Ni-like ions have a similar energy level system with the 3d10 closed ground state. Therefore, the investigation of the (3\({d}_{5/2}^{9}4s\))J=3 → (3\({d}_{3/2}^{9}4s\))J=2 and (3\({d}_{5/2}^{9}4s\))J=3 → (3\({d}_{5/2}^{9}4s\))J=2 transitions with the present laser spectroscopy scheme is also possible. The laser spectroscopy of (3\({d}_{5/2}^{9}4s\))J=3 → (3\({d}_{5/2}^{9}4s\))J=2 transitions in Ni-like ions has already been proposed, and their transition wavelengths have been systematically investigated by theoretical calculations48. Here, we follow the systematic study to discuss the versatility of the present laser spectroscopy. Figure 5 shows the atomic number dependence of the transition energies theoretically calculated by the FAC62, along with optical E1 transition energies of Ag-like ions for comparison. In the Z > 60 region, Pd-like ions are not shown because they are not suitable for the present laser spectroscopy since the (4\({d}_{5/2}^{9}5s\))J=3 level is not metastable due to the 4d95s–4d94f level crossing63. In contrast to the typical electronic E1 transitions (e. g., 5s–5p1/2 in Ag-like ions), the present M1 transitions with a number of inner-shell electrons show a gradual increase in the transition energy with increasing atomic number. As a result, in most regions where Z > 30, transitions in either Pd- or Ni-like ions are available for laser excitation.

Fig. 5: Potential of the present laser spectroscopy for studying heavy nuclei.
figure 5

Atomic number (Z) dependence of the theoretical transition energies in Pd-like (red) and Ni-like (blue) ions, along with the transition energies of the E1 transition 5s–5p1/2 in Ag-like ions (orange) for comparison. The present transition (4\({d}_{3/2}^{9}5s\))J=2 - (4\({d}_{5/2}^{9}5s\))J=3 in 127I7+ is highlighted by the star symbol. The purple-shaded region indicates wavelength ranges where it is generally difficult for lasers to reach (<200 nm).

Full size image

The present demonstration achieved precise determination of the transition energy with an uncertainty of Δk/k0 ≃ 3 × 10−6 for the M1 transition, which is inaccessible by emission spectroscopy due to the rapid E2 decay path from the upper fine-structure level. From a technical perspective, we have succeeded in extending precision spectroscopy for trapped HCIs from spontaneously emitted transitions to include non-luminescent transitions, providing a wider variety of spectroscopic targets. This offers various opportunities, including the investigation of HCI clock candidates. Prospects of the HCI atomic clock have also spurred developments in HCI laser spectroscopy with part-per-million uncertainties. Several laser spectroscopic methods for forbidden transitions of trapped HCIs free from systematic Doppler shifts have been reported46,64. These demonstrations employed a simple fine-structure transition 2P1/2-2P3/2 in the doublet ground term of Ar13+, whose transition energy is precisely known from direct wavelength measurements using passive spectroscopy65,66, leading to recent quantum logic spectroscopy36,37. However, many potential candidates for the HCI atomic clock are not directly accessible using such passive spectroscopy because they possess complicated level structures with hyperfine splitting, and their clock transitions do not emit in plasmas owing to their long lifetime. Therefore, the extension of laser spectroscopy of HCIs to complex systems is an important challenge to overcome. The present scheme can be applied to investigate the repump transitions and measure the hyperfine-structure constants of a clock state, which are otherwise not accessible using passive spectroscopic methods.

Finally, we discuss the possibilities of other applications using the present spectroscopic technique. The time-resolved LIF detection technique can be applied to hyperfine-level-selective lifetime measurements without cascade contributions from higher levels, leading to deeper investigations of hyperfine interaction43, including hyperfine-induced-interference effects67 which have not yet been experimentally observed. The demonstration of laser spectroscopy of forbidden transitions for HCIs in a laboratory plasma is expected to trigger the development of active sensing to investigate plasma conditions such as the plasma ion temperature and magnetic field, contributing to plasma diagnostics.

Methods

Theoretical transition energy

The transition energy between the fine-structure levels in 4d95s is obtained in the framework of multi-configuration Dirac-Fock (MCDF) calculations, combined with the relativistic configuration-interaction (RCI) approach, using the atomic-structure calculation code package GRASP201841. First, MCDF calculations were performed with an active space of single- and double-electron excitation from the 4s, 4p, and 4d orbitals up to 8g. Each nl orbital (n = 5–8, l = s, p, d, f, g) is added individually, with each outer orbital optimized while keeping all inner orbitals fixed. Furthermore, to account for core–core and core–valence correlations with the inner orbitals, excitations from the 3l (l = s,  p,  d) orbitals were also included. This active space treatment led to 3,300,000 jj-coupled configurations. Moreover, corrections from the Breit interaction, that is transverse photon interaction in the low-frequency limit, and QED corrections separating the self-energy and vacuum polarization corrections, are included in the RCI calculation.

Theoretical hyperfine-structure constants

Using the GRASP2018 code, we calculated the magnetic-dipole hyperfine-structure constant Ahfs and electric-quadrupole hyperfine-structure constant Bhfs for each fine-structure level ((4\({d}_{5/2}^{9}5s\))J=3 and (4\({d}_{3/2}^{9}5s\))J=2). For the input values, the nuclear magnetic moment μI and nuclear electric-quadrupole moment QI were taken from ref. 50. GRASP2018 also provides hyperfine-structure splitting calculations taking hyperfine mixing with other fine-structure levels into account. We compared two calculation cases, i.e., with and without considering shifts due to hyperfine mixing. It was found that the resulting shift in energy for each hyperfine level would be unobservable in the experiment. Each correction for the hyperfine-structure constants was also evaluated using the same procedure as for the transition energy calculation.

Estimation of uncertainties for the theoretical values

There are several origins of uncertainties in the theoretically calculated values due to various corrections. The uncertainties in the transition energy were estimated as follows: The present MCDF-CI calculations involve valence–valence (VV), core–valence (CV), and core–core (CC) correlations. They are considered by including configurations generated from all single- and double-excitations from the 3s, 3p, 3d, 4s, 4p, 4d, and 5s orbitals to the active spaces (AS) of virtual orbitals. Here we define four virtual orbital sets as follows: AS1 = {5p, 5d, 5f, 5g}, AS2 = AS1 + {6s, 6p, 6d, 6f, 6g, 6h}, AS3 = AS2 + {7s, 7p, 7d, 7f, 7g, 7h}, and AS4 = AS3 + {8s, 8p, 8d, 8f, 8g, 8h}. We estimated the convergence with the size of the basis set by taking the difference between the transition energies calculated in the AS3 and AS4 stages (≃22 cm−1). The calculated transition energies are summarized in Supplementary Table I. The detail of the corrections in the full active space set (AS4) calculation result is shown in Supplementary Table II. We adopted this value for the uncertainty in the electron correlation calculation because additional correlations were not expected to exceed this convergence value even when considering more virtual orbitals. Another possible source of uncertainty is related to the calculated contribution from the Breit interaction. The corresponding correction value was perturbatively computed in the RCI calculation through the exchange of a single transverse photon in the low-frequency limit41,68. Comparing the Breit contributions obtained from the perturbative approach to calculations in which the Breit term is included in a variational SCF process allows us to estimate the uncertainty due to the perturbative approach69,70. Previous studies have found that the magnitude of this effect is less than 0.3% in the Ni-like case (among others)69,70 and that it is significantly reduced when the active space is expanded. Here, we assume the maximum error owing to the perturbative treatment and adopt a 0.5% uncertainty related to the Breit correction. The resulting uncertainty is 2 cm−1. The QED contributions were smaller than the uncertainties related to correlation effects. Thus, the resulting uncertainty associated with these terms was negligible. The uncertainty in the Dirac-Fock term is caused by the uncertainty in the root-mean-square of the nuclear radius, which is insignificant for 127I (≃0.008 fm71). The total uncertainty was calculated by applying the error propagation rule (quadratic summation) to individual sources of uncertainty. This yielded an uncertainty in the theoretical transition energy of 22 cm−1. This uncertainty is strongly dominated by the electron correlation. We also estimated the uncertainty for each Ahfs and Bhfs constant by employing the same procedure adopted for the transition energy.

Simulation of the Zeeman splitting

The Zeeman splitting for each hyperfine level was calculated using the HFSZEEMAN95 package72,73, which is based on inputs from GRASP201841. This calculation employs an accurate treatment of the intermediate field regime; therefore, the calculated splittings are reliable for a wide range of magnetic fields. Figure 2c shows the differences in the Zeeman splitting between the initial and excited levels of the laser transition.

Simulation of the transition intensities

The hyperfine-structure-resolved Einstein A coefficients were obtained by the summation of the Einstein A coefficients for every ΔmF = 0 transition at each initial hyperfine-structure level. The transition rate for an M1 transition between magnetic hyperfine-structure sub-levels \({{{\Gamma }}}^{{\prime} }{m}_{F}^{{\prime} }\) and ΓmF is given by

$$A({{{\Gamma }}}^{{\prime} }{m}_{F}^{{\prime} }\to {{\Gamma }}{m}_{F}) =\frac{2.69735\times 1{0}^{13}}{{\lambda }^{3}}\mathop{\sum}\limits_{q}| \left\langle {{\Gamma }}{m}_{F}\right\vert {M}_{q}^{(1)}\left\vert {{{\Gamma }}}^{{\prime} }{m}_{F}^{{\prime} }\right\rangle {| }^{2},$$
(1)

where M(1) is the magnetic-dipole operator, and λ is the transition wavelength (in Å). Using the wavefunction expansion of the magnetic hyperfine substates,

$$| {{\Gamma }}{m}_{F} > =\mathop{\sum}\limits_{\gamma ,J,F}{d}_{\gamma ,J,F}| \gamma IJF{m}_{F} > $$
(2)

together with the Wigner–Eckart theorem (the dipole operator only acts on the electronic space, so we may decouple the nuclear and electronic parts in the reduced matrix element), Eq. (1) can be re-written as73

$$A({{{\Gamma }}}^{{\prime} }{m}_{F}^{{\prime} }\to {{\Gamma }}{m}_{F})=\\ \frac{2.69735\times 1{0}^{13}}{{\lambda }^{3}}\mathop{\sum}\limits_{q}| \mathop{\sum}\limits_{\gamma JF}\mathop{\sum}\limits_{{\gamma }^{{\prime} }{J}^{{\prime} }{F}^{{\prime} }}{d}_{\gamma JF}{d}_{{\gamma }^{{\prime} }{J}^{{\prime} }{F}^{{\prime} }}\\ \sqrt{(2{F}^{{\prime} }+1)(2F+1)}{(-1)}^{F-{m}_{F}}\\ \left(\begin{array}{rcl}F&1&{F}^{{\prime} }\\ -{m}_{F}&q&{m}_{F}^{{\prime} }\end{array}\right){(-1)}^{I+{J}^{{\prime} }+F+1}\\ \left\{\begin{array}{ccc}J&F&I\\ {F}^{{\prime} }&{J}^{{\prime} }&1\end{array}\right\}\left\langle \gamma J\right\vert | {M}^{(1)}| \left\vert {\gamma }^{{\prime} }{J}^{{\prime} }\right\rangle {| }^{2}.$$
(3)

Here, dγJF are the expansion coefficients, and \(\left\langle \gamma J\right\vert | {M}^{(1)}| \left\vert {\gamma }^{{\prime} }{J}^{{\prime} }\right\rangle\) is the reduced transition matrix element between the fine-structure levels. The A coefficients for all M1 transitions were calculated using the HFSZEEMAN95 package72,73. Finally, we sum the Einstein A coefficients for the ΔmF = 0 transitions of every mF sub-level and obtained the transition intensities gA of the M1 transitions, as shown in Fig. 2b.

Fitting model

We determined the hyperfine-structure constants Ahfs, Bhfs, \({A}_{hfs}^{{\prime} }\), \({B}_{hfs}^{{\prime} }\) and the fine-structure transition wavenumber k0 using the following model equation to fit experimental data:

$$f(k) = {I}_{0}\mathop{\sum}\limits_{| {F}^{{\prime} }-F| \le 1}g{A}_{{F}^{{\prime} }F}\exp \left(\frac{4\ln 2(k-({k}_{0}+{k}_{{F}^{{\prime} }F}))}{{k}_{D}^{2}}\right).$$
(4)

Here, it is assumed that each line profile is defined by a Gaussian function with the same linewidth because the hyperfine splitting energies are significantly smaller than the fine-structure transition energy. kD represents the full-width at half maximum (FWHM) of the transition line profiles. For \(g{A}_{{F}^{{\prime} }F}\), we employed theoretically calculated results for the relative transition intensities, as described in the previous section. k0 is the original transition energy between the fine-structure levels ((4\({d}_{5/2}^{9}5s\))J=3 → (4\({d}_{3/2}^{9}5s\))J=2). \({k}_{{F}^{{\prime} }F}\) is the hyperfine-structure shift for each transition given by

$${k}_{{F}^{{\prime} }F}={k}_{{F}^{{\prime} }}-{k}_{F}.$$
(5)

\({k}_{F}^{{\prime} }\) and kF are hyperfine-structure shifts from the original level for (4\({d}_{3/2}^{9}5s\))J=2 and (4\({d}_{5/2}^{9}5s\))J=3, respectively. The hyperfine splitting at each fine-structure level is given by

$${k}_{{F}^{{\prime} }} = \frac{1}{2}{A}_{hfs}^{{\prime} }{C}^{{\prime} }+{B}_{hfs}^{{\prime} }\frac{\frac{3}{4}{C}^{{\prime} }({C}^{{\prime} }+1)-I(I+1){J}^{{\prime} }({J}^{{\prime} }+1)}{2I(2I-1){J}^{{\prime} }(2{J}^{{\prime} }-1)}$$
(6)

and

$${k}_{F} = \frac{1}{2}{A}_{hfs}C+{B}_{hfs}\frac{\frac{3}{4}C(C+1)-I(I+1)J(J+1)}{2I(2I-1)J(2J-1)}.$$
(7)

Here, \({C}^{{\prime} }\) and C are given by:

$${C}^{{\prime} }={F}^{{\prime} }({F}^{{\prime} }+1)-{J}^{{\prime} }({J}^{{\prime} }+1)-I(I+1)$$
(8)

and

$$C=F(F+1)-J(J+1)-I(I+1).$$
(9)

Under the assumption of a Maxwellian distribution, the equation for the ion temperature and spectral linewidth is given by:

$$T=\frac{M{c}^{2}}{8{k}_{B}ln2}{\left(\frac{{k}_{D}}{{k}_{0}}\right)}^{2},$$
(10)

where M, c, and kB are the particle mass, speed of light, and Boltzmann constant, respectively. Equation (10) can be re-written as:

$${k}_{D}=\sqrt{\frac{8T{k}_{B}ln2}{M}}\frac{{k}_{0}}{c}.$$
(11)

Equations (11) and (4) provide theoretical spectra.