Introduction

In systems that exhibit second-order phase transitions, a disordered phase on one side of the transition, such as a liquid or glass state, can be characterized by the presence of topological defects, while on the other side of the transition, there is an ordered or defect-free state such as a crystal. The defect-free ordered phase arises when the parameter controlling the transition is changed very slowly so that the system remains within the adiabatic limit. If the rate of change through the transition increases, a portion of the topological defects do not have time to annihilate, and persist on the ordered side of the transition. A scenario for understanding the behavior for varied quench rates across a continuous phase transition is the Kibble–Zurek (KZ) mechanism, which predicts a universal power law for the defect density \({\rho }_{{{{{{{{\rm{d}}}}}}}}}\propto {t}_{{{{{{{{\rm{q}}}}}}}}}^{-\beta }\), where tq is the time duration of the quench through the transition, so that slower quenches produce fewer defects1,2,3,4. The KZ mechanism has been studied in a variety of systems at the transition into an ordered phase, where the scaling exponents can be related to the universality class of the underlying phase transition5,6,7,8,9,10,11.

The KZ scenario has generally been applied to systems that have equilibrium phase transitions; however, there have been recent proposals to use the KZ scenario to address transitions between different nonequilibrium steady states12,13,14,15,16,17, such as those that occur in optical systems or for Rayleigh–Bènard convection, where defects can arise in otherwise hexagonal ordered lattices. More recently, there has also been work examining KZ scenarios in nonequilibrium quantum systems18,19,20 including dissipative systems19. In these works, the transitions were of the Berezinskii–Kosterlitz–Thouless type, which also appears in equilibrium systems; however, these works indicate that the KZ scenario can be applied more broadly to nonequilibrium systems.

Another class of nonequilibrium systems consists of assemblies of particles driven over quenched disorder that exhibit behavior consistent with a continuous phase transition from a disordered state to an ordered state21,22,23,24,25 or from a dynamical fluctuating state to a non-fluctuating state26,27,28,29. This phenomenon is often described in terms of an absorbing phase transition in the directed percolation (DP) class, which is observed in a wide range of nonequilibrium systems26. The DP transition is particularly interesting since it is an example of a pure nonequilibrium transition that cannot occur in an equilibrium system. If the KZ scenario could be observed in a system with a DP or absorbing phase transition, this would pave the way to applying the KZ analysis to an entirely new class of nonequilibrium systems. Such systems have several features that make them ideal for studying the KZ scenario. They often contain very well-defined topological defects, and the transition can occur at T = 0, so thermal effects such as critical coarsening on the ordered side of the transition are absent and very large systems are experimentally accessible.

One of the best examples of a system that shows evidence for a continuous nonequilibrium phase transition as a function of a continuously changing driving parameter from a disordered fluctuating state with a high density of topological defects to a dynamically ordered non-fluctuating state in which topological defects are scarce or absent is superconducting vortices driven over quenched disorder21,22,30,31,32,33,34,35,36,37,38,39,40,41. At T = 0 and in the absence of quenched disorder, a superconducting vortex system forms a triangular lattice-free of defects; however, when the quenched disorder is present, a disordered state containing numerous topological defects can appear that can be characterized as a vortex glass42. A finite external drive in the form of an applied current causes vortices in the disordered state to depin and move24,42. For drives above depinning, the system enters a strongly fluctuating or plastically flowing state in which there is a fluctuating number of topological defects, while at higher drives, there is a critical driving force above which the vortices dynamically order into a state with zero or a small number of topological defects22,24,32,33,34,35,36,37. This ordered state is not isotropic but takes the form of a moving anisotropic crystal24,33,34,36,37 or a moving smectic state32,34,35,36,37,38. Here, a small number of topological defects in the form of dislocations are present which have their Burgers vectors aligned in the direction of the drive. The critical drive amplitude at which the ordering transition occurs is a function of vortex density and disorder strength24. The ordering transition has been observed experimentally by direct imaging36,39, neutron scattering30, changes in the noise37,38,41, and changes in transport curve features21,24,31,32,33,37,40. This same type of dynamical ordering transition is general to the broader class of particle-like assemblies driven over quenched disorder, and it has been studied for colloidal particles moving over disordered landscapes23,24,43,44,45, moving Wigner crystals46, sliding charged systems47, driven pattern forming states48,49, driven dislocations50, and magnetic skyrmions moving over quenched disorder51. Since the transition from the disordered state to the ordered state is controlled by changing the driving amplitude, the number of topological defects on the ordered side of the transition can be measured for varied drive sweep rates across the transition to test the predictions of the KZ scenario.

Here we explore the question of whether the KZ scenario is obeyed for nonequilibrium phase transitions in driven systems with a quenched disorder for varied sweep rates through the transition. We numerically examine the density of defects in driven vortex and colloidal systems at T = 0 for varied driving sweep rates through the dynamical ordering transition. We find that the defect density obeys \({\rho }_{{{{{{{{\rm{d}}}}}}}}}\propto {\tau }_{{{{{{{{\rm{q}}}}}}}}}^{\beta }\), where tq is the time required to go through the transition, consistent with the KZ scenario. The same behavior appears for various values of the quenched disorder and for both vortices and colloids moving over a random substrate. The exponent we find in both systems is β ≈ 0.39, consistent with an underlying transition that falls in a directed percolation (DP) universality class, which often describes nonequilibrium phase transitions from fluctuating states to non-fluctuating states26,27,29. These results could be tested experimentally in superconducting vortex systems, colloids, or other driven systems with quenched disorder. Our results also imply that the KZ mechanism could be applied generally to nonequilibrium phase transitions in the same way that it has been applied to equilibrium phase transitions, and that it could be tested in many other types of driven systems that show dynamical continuous transitions from disordered to ordered states.

Results

Modeling and characterization of the nonequilibrium phase transition

We use a well-established simulation model for superconducting vortices driven over random disorder. The vortices are represented as repulsively interacting point particles which undergo a dynamical ordering transition from a disordered plastic flow phase to a moving ordered crystal or smectic state22,24,32,33,37,38. We consider a two-dimensional (2D) system of size L × L, with L = 36λ in units of the London penetration depth, containing a fixed number N of vortices produced by an external magnetic field \({{{{{{{\bf{B}}}}}}}}=B\hat{{{{{{{{\bf{z}}}}}}}}}\). The vortex density is nv = N/L2. The motion of vortex i at position Ri is obtained by integrating the overdamped equation of motion

$$\eta \frac{d{{{{{{{{\bf{R}}}}}}}}}_{i}}{dt}={{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{vv}}}}}}}}}+{{{{{{{{\bf{F}}}}}}}}}_{i}^{{{{{{{{\rm{pp}}}}}}}}}+{{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}},$$
(1)

where the damping constant η = 1.0. The vortex–vortex interaction force \({{{{{{{{\bf{F}}}}}}}}}_{i}^{{{{{{{{\rm{vv}}}}}}}}}=\mathop{\sum }\nolimits_{j = 1}^{N}{f}_{0}{K}_{1}({R}_{ij}/\lambda ){\hat{{{{{{{{\bf{R}}}}}}}}}}_{ij}\), where K1 is the modified Bessel function, Rij = ∣Ri − Rj∣ is the distance between vortex i and j, \({\hat{{{{{{{{\bf{R}}}}}}}}}}_{ij}=({{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{j})/{R}_{ij}\), \({f}_{0}={\phi }_{0}^{2}/2\pi {\mu }_{0}{\lambda }^{3}\), μ0 is the permeability of free space, and ϕ0 = h/2e is the elementary flux quantum. The modified Bessel function K1 falls off exponentially for Rij/λ > 1.0. The vortices are confined to the x, y plane and the magnetic field is applied in the z-direction. The quenched disorder is modeled by Np randomly placed harmonically attractive pinning sites of radius rp with \({{{{{{{{\bf{F}}}}}}}}}_{i}^{{{{{{{{\rm{pp}}}}}}}}}=-\mathop{\sum }\nolimits_{k = 1}^{{N}_{{{{{{{{\rm{p}}}}}}}}}}({F}_{{{{{{{{\rm{p}}}}}}}}}/{r}_{{{{{{{{\rm{p}}}}}}}}})({{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{k}^{{{{{{{{\rm{(p)}}}}}}}}}){{\Theta }}({r}_{{{{{{{{\rm{p}}}}}}}}}-| {{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{k}^{{{{{{{{\rm{(p)}}}}}}}}}| ){\hat{{{{{{{{\bf{R}}}}}}}}}}_{ik}^{{{{{{{{\rm{(p)}}}}}}}}}\) where Fp is the maximum pinning force, \({{{{{{{{\bf{R}}}}}}}}}_{k}^{{{{{{{{\rm{(p)}}}}}}}}}\) is the location of pinning site k, and \({\hat{{{{{{{{\bf{R}}}}}}}}}}_{ik}^{{{{{{{{\rm{(p)}}}}}}}}}=({{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{k}^{{{{{{{{\rm{(p)}}}}}}}}})/| {{{{{{{{\bf{R}}}}}}}}}_{i}-{{{{{{{{\bf{R}}}}}}}}}_{k}^{{{{{{{{\rm{(p)}}}}}}}}}|\). The pinning density is np = Np/L2. The driving force Fd is applied uniformly to all the vortices, and corresponds experimentally to a Lorentz force \({{{{{{{{\bf{F}}}}}}}}}_{{{{{{{{\rm{d}}}}}}}}}={{{{{{{\bf{B}}}}}}}}\times {{{{{{{\bf{J}}}}}}}}={F}_{{{{{{{{\rm{D}}}}}}}}}{f}_{0}\hat{{{{{{{{\bf{x}}}}}}}}}\), where J is the applied current. The initial vortex configurations are obtained using simulated annealing. We increase the magnitude of the dimensionless driving force from FD = 0 to a final maximum value over a total time of tq in increments of ΔFD = 0.002. Time is reported in dimensionless units achieved by scaling time by τ = η/f0. We characterize the system by measuring the average velocity per vortex in the driving direction, \(\left\langle V\right\rangle ={N}^{-1}\mathop{\sum }\nolimits_{i}^{N}{{{{{{{{\bf{v}}}}}}}}}_{i}\cdot \hat{{{{{{{{\bf{x}}}}}}}}}\), and the fraction of sixfold coordinated vortices, \({P}_{6}={N}^{-1}\mathop{\sum }\nolimits_{i}^{N}\delta ({z}_{i}-6)\), where zi is the coordination number of vortex i obtained from a Voronoi construction. We also compute the fraction of topological defects PD = 1 − P6.

Numerical results

Figure 1 illustrates the effect of changing FD in the adiabatic limit for a system with nv = 1.0, np = 0.5, Fp = 0.4, and rp = 0.3. In Fig. 1a we plot the average vortex velocity \(\left\langle V\right\rangle\) along with \(d\left\langle V\right\rangle /d{F}_{{{{{{{{\rm{D}}}}}}}}}\) versus FD for tq = 7.5 × 106. If tq is increased to a larger value, the curves remain nearly unchanged. Figure 1b shows the corresponding fraction of sixfold coordinated vortices P6 versus FD, where we would have P6 = 1 for a triangular lattice. A depinning transition occurs near FD = 0.06, and for FD < 0.225 we find P6 ≈ 0.64, indicating a highly defected or disordered state in which the vortices are undergoing plastic flow. In Fig. 2a we show a Voronoi plot of a snapshot of the vortex positions from the system in Fig. 1 at FD = 0.1, where numerous dislocations are present. As Fig. 1b indicates, for FD > 0.4 there is a regime in which P6 increases until it reaches the value P6 = 0.98, where the vortices form an anisotropic triangular lattice of the type shown in Fig. 2b at FD = 1.5 in the ordered state. Here the lattice is aligned in the driving direction and contains a small number of aligned dislocations, forming a smectic state as studied previously32,33,34,36,37. The critical force for the transition from the disordered state to the dynamically ordered phase is \({F}_{{{{{{{{\rm{D}}}}}}}}}^{{{{{{{{\rm{c}}}}}}}}}\approx 0.3\). We do not observe any hysteresis across the transition, which has features consistent with a second-order transition. In Fig. 1a, there is a peak in \(d\left\langle V\right\rangle /d{F}_{{{{{{{{\rm{D}}}}}}}}}\) in the plastic flow phase near FD = 0.15 followed by a saturation near FD = 0.3 to \(d\left\langle V\right\rangle /d{F}_{{{{{{{{\rm{D}}}}}}}}}\approx 1.0\), in agreement with previous studies of the dynamical ordering transition21,31,33,38,40,41. The critical driving force for dynamic ordering also depends on the strength of the disorder, as shown in Fig. 1c where we plot a dynamical phase diagram for the system in Fig. 1a, b as a function of Fp versus FD at tq = 7.5 × 106. The disordered and ordered phases are highlighted, and the arrow illustrates the direction in which we sweep across the transition at different rates.

Fig. 1: Dynamical phase transition in a superconducting vortex system.
figure 1

a The velocity \(\left\langle V\right\rangle\) versus applied drive FD (blue) and the corresponding \(d\left\langle V\right\rangle /d{F}_{{{{{{{{\rm{D}}}}}}}}}\) vs FD (red) for a 2D superconducting vortex system with quenched disorder at vortex density nv = 1.0, pinning density np = 0.5, pinning force Fp = 0.4, and pinning radius rp = 0.3. The curves are from a single simulation and are obtained for a quenching time of tq = 7.5 × 106, which is considered the adiabatic limit. b The corresponding fraction of sixfold coordinated vortices P6 vs FD. A nonequilibrium transition from a disordered state to an ordered state occurs for FD ≈ 0.3. c Dynamical phase diagram as a function of Fp versus FD for the same system highlighting the disordered phase (green) and the dynamically ordered phase (blue). The arrow indicates the direction in which the transition is crossed at different sweep rates. The error bars representing the uncertainty in the location of the depinning transition, obtained from multiple realizations, are smaller than the symbols.

Full size image
Fig. 2: Vortex configurations on either side of the dynamical phase transition.
figure 2

Voronoi constructions of snapshots of the vortex positions in the system from Fig. 1 with vortex density nv = 1.0, pining density np = 0.5, pinning force Fp = 0.4, pinning radius rp = 0.3, and quench time tq = 7.5 × 106. White polygons are sixfold coordinated, red polygons are sevenfold coordinated, and blue polygons are fivefold coordinated. a A driving force of FD = 0.1 in the disordered phase with numerous defects. (b) FD = 1.5 in the dynamically ordered phase. The vortex lattice is aligned in the driving direction and there is a small number of aligned dislocations.

Full size image

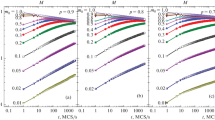
Now that we have established the driving force which separates the disordered and ordered phases, we can cross this transition for varied tq. In Fig. 3a we plot P6 versus FD for the system in Fig. 1 at tq = 7.5 × 106, 3 × 106, 7.5 × 105, 3 × 105, 7.5 × 104, 3 × 104, 7.5 × 103, 3 × 103, and 750, showing that as the quench rate increases and tq becomes smaller, the fraction of sixfold coordinated particles on the ordered side of the critical transition value \({F}_{{{{{{{{\rm{D}}}}}}}}}^{{{{{{{{\rm{c}}}}}}}}}=0.3\) drops. The final defect density as a function of tq appears in Fig. 3b, c.

Fig. 3: Transition from the disordered to the ordered state for superconducting vortices as a function of quenching speed.
figure 3

a The fraction of sixfold coordinated vortices P6 versus driving force FD for the system in Fig. 1 with vortex density nv = 1.0, pinning density np = 0.5, pinning force Fp = 0.4, and pinning radius rp = 0.3 at quench times of tq = 7.5 × 106, 3 × 106, 7.5 × 105, 3 × 105, 7.5 × 104, 3 × 104, 7.5 × 103, 3 × 103, and 750, from top to bottom. b The final defect density PD = 1 − P6 at FD = 1.5 in the same system versus tq. The solid line is a power-law fit with exponent β = −0.385. c PD versus tq for the same system at different values of Fp = 0.2 (blue squares), 0.4 (red circles), 0.6 (green diamonds), 0.8 (blue up triangles), 1.0 (orange right triangles), and 1.2 (purple down triangles). The solid line is a power-law fit with β = −0.39. Error bars in (b, c) representing the uncertainty in the defect density, obtained from multiple realizations, are smaller than the data markers.

Full size image

We illustrate Voronoi plots of the final FD = 1.5 state for the system in Fig. 3 at tq = 7.5 × 103 in Fig. 4(a), tq = 3 × 104 in Fig. 4b, tq = 7.5 × 104 in Fig. 4c, and tq = 3 × 105 in Fig. 4d, indicating that the number of remaining defects is larger for smaller tq. Figure 2b shows the same sample in the adiabatic limit with tq = 7.5 × 106. The defects that appear on the ordered side of the transition generally take the form of dislocations composed of pairs of fivefold and sevenfold coordinated particles. At larger tq, the dislocations have their Burgers vectors oriented in the direction of drive, giving rise to a smectic ordering in which the system can be regarded as a set of one-dimensional (1D) moving channels. In Fig. 3b we plot PD = 1 − P6, the density of topological defects at the final FD = 1.5 state on the ordered side of the transition, versus tq. We find \({P}_{{{{{{{{\rm{D}}}}}}}}}\propto {t}_{{{{{{{{\rm{q}}}}}}}}}^{\beta }\), where the solid line indicates a fit with β = −0.385. The KZ scenario predicts a power-law decay of PD with increasing tq. If we choose a final value of FD which is closer to but still above the critical transition drive Fc, the scaling is not as good at smaller tq but we still find the same exponent for the larger values of tq.

Fig. 4: Final ordering of lattice at different quenching speeds.
figure 4

Voronoi plots of the final driving force FD = 1.5 state for the system in Fig. 3a, b with vortex density nv = 1.0, pinning density np = 0.5, pinning force Fp = 0.4, and pinning radius rp = 0.3 at quench times of (a) tq = 7.5 × 103, (b) 3 × 104, (c) 7.5 × 104, and (d) 3 × 105. The number of defects is larger for smaller tq or a faster sweep rate.

Full size image

The plots of PD versus tq in Fig 3c indicate that the same scaling behavior remains robust over a range of different values of Fp from Fp = 0.2 to Fp = 1.2. Since Fc varies with Fp, for each sample we select a final value of FD that is the same distance above Fc for consistency. The straight line is a power-law fit with β = 0.39. For large Fp, the scaling at larger values of tq is not as good because more defects become trapped by the pinning.

In addition to superconducting vortices, we have also considered colloidal particles driven over quenched disorder. Here we use the same type of overdamped simulations but replace the particle–particle interactions with the Yukawa or screened Coulomb potential \(U({r}_{ij})=A\exp (-\kappa {r}_{ij})/{r}_{ij}\)52, with κ = 1.0 and A = 0.1. The colloidal particles experience a stronger short-range repulsion than the vortices. In experiments, various types of random quenched disorder can be introduced along with an external driving force45,53, and the number of topological defects can be measured with imaging techniques53,54. In Fig. 5a we show P6 versus FD in a colloidal system with colloidal density nc = 1.0, np = 0.5, Fp = 1.0, and rp = 0.35 at tq = 3 × 106, 7.5 × 105, 3.0 × 105, 7.5 × 104, 3.0 × 104, 7.5 × 103, 750, 300, and 75, where the final P6 decreases for smaller tq. In Fig. 5b we plot the final value of PD at FD = 2.5 versus tq for the system in Fig. 5a. The solid line is a power-law fit with β = −0.39, similar to the exponent obtained for the vortex case.

Fig. 5: Transition from the disordered to the ordered state for colloidal particles as a function of quenching speed.
figure 5

a The fraction of sixfold coordinated colloids P6 versus driving force FD for a colloidal system with colloid density nc = 1.0, pinning density np = 0.5, pinning force Fp = 1.0, and pinning radius rp = 0.35 at quench times of tq = 3 × 106, 7.5 × 105, 3.0 × 105, 7.5 × 104, 3.0 × 104, 7.5 × 103, 750, 300, and 75, from top to bottom. b The defect density PD vs tq for the system in (a) obtained at FD = 2.5. The solid line is a power-law fit with exponent β = −0.39. Error bars representing the uncertainty in the defect density, obtained from multiple realizations, are smaller than the data markers.

Full size image

Discussion

We can ask whether the scaling exponent we obtain can be related to possible universality classes of the dynamical transition. In the KZ scenario, the scaling exponent obeys β = (D − d)ν/(1 + zν), where ν and z are critical exponents associated with the universality class of the underlying phase transition, D is the spatial dimension of the system, and d is the dimension of the defect. For a 2D Ising model with D = 2, β = 2/3, which is not what we observe; however, since the defects in our sample are all aligned in the driving direction, our system is closer to coupled 1D channels, which would give β = 1/3. Recent simulations of certain quenched 2D spin ice models give β = 0.3155. A more likely candidate for the universality class of a nonequilibrium system is directed percolation (DP)26, where the critical exponents depend on the effective dimension of the dynamics. If we assume dynamics of dimension 1 + 1, we would have z = 1.58 and ν = 1.09726, giving β = 0.401, which is in agreement with the values we observe. We argue that the 1 + 1 dynamics may be relevant since the topological defects are mostly aligned in a single direction on the ordered side of the transition, and the relevant length scale could be the distance between the defects in the direction of the drive rather than perpendicular to the drive.

In the KZ scenario, the lag time between the nonequilibrium and equilibrium value is given by the freeze-out time \(\hat{t}\propto {({t}_{{{{{{{{\rm{q}}}}}}}}}^{z\nu })}^{\frac{1}{1+z\nu }}\)4. Since the value of the driving force FD is a function of time, and since FD and tq are dimensionless, this implies that the defect fraction should scale as \({P}_{{{{{{{{\rm{D}}}}}}}}}\propto {F}_{{{{{{{{\rm{D}}}}}}}}}/{t}_{{{{{{{{\rm{q}}}}}}}}}^{\alpha }\), where tq is the quench time. In Fig. 6a we illustrate this scaling for the vortex system from Fig. 3a and in Fig. 6b we show the scaling for the colloidal system from Fig. 5a. In each case, the scaling exponent is α = 0.625. The KZ prediction gives zν/(1 + zν) = α, where plugging in the scaling exponents for 1 + 1 directed percolation26 leads to α = 0.632, consistent with the exponents we find.

Fig. 6: Defect density scaling in the vortex and colloid systems.
figure 6

Dimensionless scaling plots of the defect density PD versus the scaled driving force \({F}_{{{{{{{{\rm{D}}}}}}}}}/{t}_{{{{{{{{\rm{q}}}}}}}}}^{\alpha }\), where tq is the quench time and where the exponent α = 0.625. a The vortex system from Fig. 3a. b The colloid system from Fig. 5a.

Full size image

To better understand why the dynamics is 1 + 1 dimensional, in Fig. 7a we illustrate the colloidal positions and trajectories on the disordered side of the transition for a subset of the system in Fig. 5 at FD = 0.25 and tq = 7.5 × 105, showing strongly disordered flow occurring in both the x and y directions. The corresponding Voronoi plot in Fig. 7b contains a high defect density, similar to what is observed in the vortex system in the disordered phase. Figure 7c shows the positions and trajectories of the colloids on the ordered side of the transition at FD = 1.5. Here the dynamics are strictly 1D in character, and the topological defects are all aligned in the direction of the drive as shown in Fig. 7d. In theoretical work for particles moving over random disorder in 2D, it is argued that the strongly driven case can be considered as a series of coupled 1D channels that slide past one another to form a moving smectic state34,35. This 1D channeling could explain why the dynamics produce scaling exponents consistent with 1 + 1 DP rather than 2 + 1 DP.

Fig. 7: Disordered and 1 + 1 dimensional flow below and above the dynamical phase transition.
figure 7

a The colloid positions (red circles) and trajectories (lines) for a subset of the system in Fig. 5 with colloid density nc = 1.0, pinning density np = 0.5, pinning force Fp = 1.0, and pinning radius rp = 0.35 at a quench time of tq = 7.5 × 105 and a driving force of FD = 0.25, showing 2D disordered flow. b The corresponding Voronoi plot showing a high defect density. c The colloid positions and trajectories in the same system at FD = 1.5 showing 1D channeling. d The corresponding Voronoi plot shows that all of the topological defects are aligned in the same direction.

Full size image

As indicated in the introduction, the KZ scenario has previously been demonstrated in nonequilibrium systems18,19,20; however, these systems are of a different type than the driven particles over the quenched disorder that we consider, and the transitions are versions of equilibrium phase transitions such as the Berezinskii–Kosterlitz–Thouless transition. In our system, the transition is an absorbing phase transition in the directed percolation class26,27,28,29, which has no equilibrium analog, so our results open the possibility of applying the KZ scenario to a new class of nonequilibrium phase transitions of DP type. In the past, directed percolation systems were very difficult to characterize, and experiments providing strong evidence for the DP transition were first achieved relatively recently27,28. Our work suggests that the KZ scenario can be used as a valuable way to characterize systems with absorbing phase transitions. Additionally, since very large-scale experiments can be performed for driven particles over quenched disorder, extensive KZ scaling regimes could be accessed in these systems. Other directions include studying the statistics of the defect distribution56 or considering very slow annealing57.

In conclusion, we have investigated the evolution of the density of defects across a dynamical disorder to order nonequilibrium phase transition for driven particles moving over quenched disorder as we vary the quench rate. We find that the defect density scales as a power law with quench rate, in agreement with the predictions of the Kibble–Zurek scenario. For both superconducting vortices and colloidal assemblies, we find a scaling exponent of β ≈ −0.39, which is consistent with an underlying transition that falls in the 1 + 1 directed percolation universality class since the ordered system forms a moving smectic state in which the defects are aligned in 1D chains. Experimentally, our predictions could be tested in superconducting vortex systems using various imaging and transport measures that have previously been shown to be correlated with the number of defects in the vortex lattice31. Direct imaging of the dynamics is feasible using colloidal systems, and it would also be possible to consider ac drives which would avoid edge effects. Our results suggest that the Kibble–Zurek scenario can be applied to more general nonequilibrium continuous absorbing phase transitions, particularly those between disordered strongly fluctuating states and ordered weakly fluctuating or non-fluctuating states. Our results also imply that a system undergoing a directed percolation transition could exhibit features of the Kibble–Zurek scenario provided that some type of well-defined defect structure can be identified.