Long-living carriers in a strong electron–phonon interacting two-dimensional doped semiconductor

Abstract

Carrier doping by the electric field effect has emerged as an ideal route for monitoring many-body physics in two-dimensional materials where the Fermi level is tuned so that the strength of the interactions can also be scanned. The possibility of systematic doping together with high resolution photoemission has allowed to uncover a genuinely many-body electron spectrum in single-layer MoS₂ transition metal dichalcogenide, resolving three clear quasi-particle states, where only one should be expected if the electron–phonon interaction vanished. Here, we combine first-principles and consistent complex plane analytic approaches and bring into light the physical origin of the two gaps and the three quasi-particle bands which are unambiguously present in the photoemission spectrum. One of these states, though being strongly interacting with the accompanying virtual phonon cloud, presents a notably long lifetime which is an appealing property when trying to understand and take advantage of many-body interactions to modulate transport properties.

Introduction

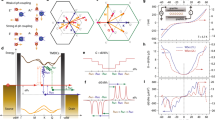
The effective velocity and the lifetime of electron states close to the Fermi level determine most of the transport properties of metals, and the interactions with collective excitations, e.g., phonons, magnons, or plasmons, are responsible for modifying or renormalizing these properties¹. Specifically, phonons are the low energy excitations that more strongly couple to electron states in normal metals². The interaction of electrons and phonons has a many-body character primarily because the Pauli exclusion principle prohibits the scattering to occupied states and because quantum mechanics allows the virtual excitation of phonons even in the absence of available energy for low energy electrons. All this physics is already contained in the most drastically simplified Einstein model, where one single optical phonon mode with energy $\omega _0$ interacts with a single electron band with a parabolic dispersion in the absence of coupling (Fig. 1a)³. The many-body coupling divides the spectrum in two regions, below and above $\omega _0$. On the one hand, for energies below $\omega _0$, electrons do not have sufficient energy for emitting any phonon, and therefore they appear long lived. However, they are allowed to emit and reabsorb phonons in virtual processes, which produces an entire phonon cloud around electrons having the effect of augmenting their effective mass, similar to polaron states in insulators⁴. On the other hand, for electrons above $\omega _0$ the emission of phonons is now allowed, the effect being that virtual processes are less probable in favor of real emission of phonons leading to a decreasing of their lifetime and effective mass. This idealized picture will be useful for understanding the more intricate situation in MoS₂ and questions the simple view about quasi-particle properties themselves, since the interaction with phonons produces two different electron states with radically different properties. A bit more technically, as the energies of quasi-particle states are determined by the poles of the electron propagation amplitude or Green’s function ($G({\mathbf{k}},z)$)⁵, the presence of several poles in this function evidences the existence of as many quasi-particle states (Fig. 1b), with very different physical properties in terms of lifetime and dispersion (Fig. 1c, d). Similarly, in a simple system consisting of two optical phonon modes with different energies, the electron band would split twice when reaching the energy corresponding to each phonon mode.

Fig. 1

Schematic picture of a coupled electron–phonon system. a A bare electron with a parabolic dispersion, represented by a solid black line ($\epsilon^0_{\mathrm{k}}$), interacts with a dispersionless phonon, represented by a dotted line ($\omega _0$). The electron decay processes by phonon emission are energetically allowed only for electrons above $\omega _0$ (red background). Therefore, the situation is completely different for electrons below this energy range, though even there, quantum field laws allow for virtual excitations of phonons. The result is that the coupling produces two excitation branches $E_1^{{\mathrm{qp}}}$ and $E_2^{{\mathrm{qp}}}$, whose dispersions are represented by blue and red solid lines, respectively. Fixing the electron momentum at k₀ (dashed line in (a)), one obtains a spectral function with two peaks at real frequencies (b) corresponding to the above pair of bands. Looking at the complex frequency plane, these two excitations are traced back to poles of the electron Green’s function and their position in the complex plane determines the renormalized energy (E^qp) and lifetime broadening (${\mathrm{\Gamma }}^{{\mathrm{qp}}}$). When most of the spectral function (coherent part) is recovered from the superposition of the separate contributions of the poles, one may say that a multiple quasi-particle picture is valid. c Electrons below $\omega _0$ are strongly renormalized and tend to localize as they are followed by a dense virtually emitted phonon cloud. d On the contrary, the higher energy band is energetically allowed to emit phonons and acquires a more extended character and a lighter effective mass

There have been many good examples of angle-resolved photoemission spectroscopy (ARPES) measurements on metal surfaces^6,7,8, high-temperature superconductors⁹, and doped polar insulators^10,11, where strong deviations from the single quasi-particle picture have been observed and attributed to the electron–phonon interaction. However, the recent measurements of Kang et al.¹² show that MoS₂ is probably the first system where a double splitting in the ARPES spectrum has been observed unambiguously, therefore the importance of understanding the physical nature of these broken bands. These results go also hand in hand with the spin-valley locking protected superconductivity found in this system¹³, and while some experimental works illustrated the superconducting state as due to the filling of ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$) valleys^14,15,16, this interpretation clashes with the picture which holds that superconductivity emerges as soon as the Fermi energy (E_F) crosses the bottom of the ${\bar{\mathrm{Q}}}$($\overline {{\mathrm{Q}}\prime }$) valleys^17,18,19. In fact, the onset of superconductivity coincides with an outstanding enhancement of the electron–phonon coupling strength¹⁷, stemming from phonon-mediated intervalley interactions on the Fermi surface (FS)^17,18,19, also in agreement with the strong softening of several phonon modes observed in the gate-induced superconducting monolayer MoS₂¹⁸. In this work, we analyze these points and more specifically the case of the observed multiple band splitting¹² in MoS₂, where the experiments seemed to point out a direct interpretation in terms of multiple-phonon excitations. Our ab initio calculations of the electron spectral function including electron–phonon effects together with the complex plane analysis of the quasiparticle poles rule out that hypothesis, and show that the singular band splitting observed in ARPES experiments can be explained by three coexisting quasi-particle states, one of which has an exceptionally long lifetime.

Results

Electron–phonon effects on the electron spectral function

We made an in-depth theoretical analysis of the electron–phonon interaction in electron-doped monolayer MoS₂ by means of first-principles calculations in order to shed light on several aspects of the electron–phonon coupling in this system (see also Methods). We chose a doping carrier density of $n_{2{\mathrm{D}}} = 9 \times 10^{13}\,{\mathrm{cm}}^{ - 2}$, for which the conduction-band minima at ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$) are filled and almost spin-degenerate (Fig. 2a) with a binding energy of $E_{{\bar{\mathrm{K}}}(\overline {{\mathrm{K}}\prime } )} = - 118\,{\mathrm{meV}}$, while only the lower spin-split states are populated at ${\bar{\mathrm{Q}}}$($\overline {{\mathrm{Q}}\prime }$) with a binding energy of $E_{{\bar{\mathrm{Q}}}(\overline {{\mathrm{Q}}\prime } )} = - 22\,{\mathrm{meV}}$, which is within the phonon energy range. The density of states (DOS) increases step-like as the 2D quasi-parabolic conduction-bands get populated, showing a noticeable enhancement with the filling of the ${\bar{\mathrm{Q}}}$($\overline {{\mathrm{Q}}\prime }$) bands (Fig. 2a), the main consequence being that, among all the possible intervalley scattering channels connecting the Fermi sheets (see Supplementary Note 1), the phonon modes with momentum ${\mathbf{q}} = {\bar{\mathrm{M}}}$ are the ones dominating the whole electron–phonon coupling (Fig. 2b). This is supported by the large value of the spin-conserving electron–phonon matrix elements (Fig. 2c) for the in-plane polarized acoustic (A) and optical (O) modes with frequencies around $\omega _{\mathrm{A}}^{{\bar{\mathrm{M}}}} = 16\,{\mathrm{meV}}$ and $\omega _{\mathrm{O}}^{{\bar{\mathrm{M}}}} = 46\,{\mathrm{meV}}$, respectively, which show the largest softenings comparing to the undoped vibrational spectrum¹⁸. Furthermore, the momentum-resolved mass enhancement parameter λ_kj (Methods) for the two occupied spin bands (Fig. 2d) definitely confirms that the electron–phonon coupling is governed by phonons with ${\mathbf{q}} = {\bar{\mathrm{M}}}$, yielding λ_kj values as large as 1.2 near ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$).

Fig. 2

Electron–phonon coupling in monolayer MoS₂ from first-principles. a Electron band structure and b corresponding density of states (DOS) (right). Dashed red (spin-up) and solid blue (spin-down) lines represent opposite out-of-plane spin-polarized bands. Fermi energy (E_F) is set to zero and marked by a horizontal dashed (black) line. $E_{{\bar{\mathrm{K}}}(\overline {{\mathrm{K}}\prime } )} = - 118\,{\mathrm{meV}}$ is the binding energy of the conduction-band minima at ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$). $E_{{\bar{\mathrm{Q}}}(\overline {{\mathrm{Q}}\prime } )} = - 22\,{\mathrm{meV}}$ is the binding energy of the minima at ${\bar{\mathrm{Q}}}$($\overline {{\mathrm{Q}}\prime }$). While ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$) valleys are almost degenerated, spin orbit (SO) interaction induces an energy splitting of Δ_SO = 70 meV at ${\bar{\mathrm{Q}}}$($\overline {{\mathrm{Q}}\prime }$) band edges. k_A momentum is represented by a vertical dotdashed (orange) line. c Fermi surface (FS) of doped MoS₂ in the Brillouin zone (BZ) including a 3D-representation of the conduction-band electron pockets centered at the ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$) and ${\bar{\mathrm{Q}}}$($\overline {{\mathrm{Q}}\prime }$) points. Green arrows depict in the left (right) panel the relevant electronic spin-conserving intervalley transitions driven by phonons with equivalent momenta close to ${\mathbf{q}} = {\bar{\mathrm{M}}}$, connecting $\overline {{\mathrm{Q}}\prime }$(${\bar{\mathrm{Q}}}$) pockets with themselves and with outer states in ${\bar{\mathrm{K}}}$($\overline {{\mathrm{K}}\prime }$) valley for spin-up (spin-down) polarization. d Phonon dispersion relation and e the corresponding phonon DOS (PDOS). The undoped and doped phonons are represented by dashed (gray) and solid (color code) lines, respectively. The color code indicates the electron–phonon weighted nesting function $\left( {\left\langle {\left| {g_\nu ^{\mathrm{q}}} \right|^2} \right\rangle _{{\mathrm{FS}}}} \right)$ for each phonon state $|{\mathbf{q}},\nu \rangle$ (see Methods). f Momentum resolved mass enhancement parameter λ_kj for the occupied spin-up (left) and spin-down (right) bands, the color code indicating its strength

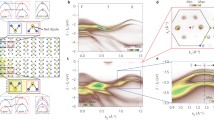
We have computed the ab initio electron spectral function $A({\mathbf{k}},\omega )$ including the electron–phonon effects without any adjustable parameter (Methods). This function displays two sharp band-splittings for electron momenta close to ${\bar{\mathrm{K}}}$ at $\omega _{\mathrm{A}}^{{\bar{\mathrm{M}}}}$ and $\omega _{\mathrm{O}}^{{\bar{\mathrm{M}}}}$ binding energies and width 22 meV (Fig. 3a–c), each of these band-splittings evoking the one sketched in Fig. 1a for the simplified Einstein model. The calculated spectral function is in close agreement with the measurements by Kang et al.¹² and describes the three spectral bands observed in experiment. We find that from the two concentric bands around the ${\bar{\mathrm{K}}}$ valley, it is the outer one (spin-up) which shows the most intense signatures of the electron–phonon coupling, as easily recognized when considering spin conservation arguments (Fig. 2d). This is also the reason why the inner spin-locked state shows much weaker spectral features. Let us now focus on the strongly interacting outer spin-split band. For this state, the frequency dependent imaginary part of the electron self-energy $({\mathrm{Im}}{\kern 1pt} {\mathrm{\Sigma }}_{{\mathbf{k}}j}(\omega ))$ at momentum ${\mathbf{k}} = k_A$ close to ${\bar{\mathrm{K}}}$ (Fig. 2a) shows a rather uncommon rectangular shaped double structure of width ~$|E_{\overline {{\mathrm{Q}}\prime } }| = 22\,{\mathrm{meV}}$ separated by a narrow window at $\omega \sim 42\,{\mathrm{meV}}$ with almost vanishing value (Fig. 3d, right). These two rectangular shapes have onsets precisely at $\omega _{\mathrm{A}}^{{\bar{\mathrm{M}}}}$ and $\omega _{\mathrm{O}}^{{\bar{\mathrm{M}}}}$ binding energies and they are easily rationalized in terms of energy conservation for the corresponding phonon emission processes connecting states close to $\overline {{\mathrm{Q}}\prime }$ with those near ${\bar{\mathrm{K}}}$ (Fig. 2b). It is actually the large DOS at the occupied $\overline {{\mathrm{Q}}\prime }$ pockets (Fig. 3d, left) which enhances the phase-space of these strongly-interacting scattering processes, yielding the maximum values of ${\mathrm{Im}}{\kern 1pt} {\mathrm{\Sigma }}_{k_A \uparrow }(\omega )$ (yellow shaded areas in Fig. 3d). The dip in the imaginary part of the self-energy appears as long as the condition $\omega _{\mathrm{O}}^{{\bar{\mathrm{M}}}} - \omega _{\mathrm{A}}^{{\bar{\mathrm{M}}}} > \left| {E_{\overline {{\mathrm{Q}}\prime } }} \right|$ holds, since the quasi-particles near ${\mathbf{k}} = k_A$ with energies between the two maxima cannot scatter to $\overline {{\mathrm{Q}}\prime }$ valleys. This means that the most uncommon spectral feature found in ARPES close to ~42 meV, also found in our calculations (Fig. 3b, c), if demonstrated to be a well-defined quasi-particle, it would correspond to a very long-lived state even if it is strongly interacting. This is a unique characteristic of MoS₂, arising from the fact that the relevant doped valleys have different binding energies and that there are basically two relevant phonon modes connecting precisely those valleys. Recall that in ordinary metals, where the DOS is practically constant for typical phonon energies, the imaginary part of the electron–phonon self-energy is a monotonically increasing function, which is radically different to what is observed in MoS₂. Note that thermal and electron–electron interactions are expected to slightly soften the spectral features obtained considering only the electron–phonon coupling. An estimation of the electron–electron interaction considering random phase approximation (RPA)²⁰ adds a slowly monotonically increasing function yielding a broadening of ${\mathrm{\Gamma }}_{{\mathrm{ee}}} \sim 2.8\,{\mathrm{meV}}$ even for electron energies close to $\omega \sim 40\,{\mathrm{meV}}$.

Fig. 3

Multiple quasi-particle spectra on monolayer MoS₂. a Spectral function of monolayer MoS₂, calculated from first-principles including electron–phonon interaction effects. The solid black lines represent the non-interacting electron bands. The dashed rectangle highlights the area of the Brillouin zone (BZ) where the strongest renormalization of the electronic bands occur. b Zoom of the spectral function of the outer spin-split band on the area highlighted in (a) with the same color code. c Three dimensional representation of (b). d Imaginary part of the electron self-energy $({\mathrm{Im}}{\kern 1pt} {\mathrm{\Sigma }}(\omega ))$ (right panel) for an electron with spin-up and momentum k_A close to ${\bar{\mathrm{K}}}$ (Fig. 2a). The onsets of the rectangular maxima are at $\omega _{\mathrm{A}}^{{\bar{\mathrm{M}}}}$ and $\omega _{\mathrm{O}}^{{\bar{\mathrm{M}}}}$, the energies of the acoustic and optical phonons at ${\mathbf{q}} = {\bar{\mathrm{M}}}$, while their width is related to the enhanced density of states (DOS) at the occupied $\overline {{\mathrm{Q}}\prime }$ pockets (yellow shaded area in left panel). e Dispersion of the three quasi-particle poles found for the outer band. The real part of the poles—quasi-particle energies—with respect to the momentum are shown by the blue ($n = 1$), green ($n = 2$), and red ($n = 3$) dots, respectively. The length of the bars represent the spectral weight of each pole, given by the real part of their residues ${\Bbb Z}_n^{{\mathrm{qp}}}$, while the imaginary part of the residues are represented by the rotation of the bars, ${\mathrm{Im}}({\Bbb Z}_n^{{\mathrm{qp}}}) = 1$ giving a rotation of $\theta _n^{{\mathrm{qp}}} = \pi$ radians. f Contribution to the spectral function coming from each complex quasi-particle pole, shown by different colors following the same convention as in (e)

Quasi-particle poles in the complex plane

It is worth looking a bit more closely at the general properties of the quasi-particles even if it is succinctly, in order to see if the observed spectral features can be defined as actual quasi-particles. These find their appropriate mathematical definition as poles of the electron Green’s function $G_{\mathbf{k}}(z) = 1/\left( {z - \epsilon _j^{\mathbf{k}} - {\mathrm{\Sigma }}_{{\mathbf{k}}j}(z)} \right)$, that is, the solutions of the so-called Dyson equation $z - \epsilon _j^{\mathbf{k}} - {\mathrm{\Sigma }}_{{\mathbf{k}}j}(z) = 0$. The key point here is that due to the nonlinear character of this equation it may lead to several solutions, even for a single unperturbed state with energy $\epsilon _j^{\mathbf{k}}$. The consistent use of the complex plane allows to treat the Green’s function in the entire plane and the energy (E^qp) and the lifetime broadening (${\mathrm{\Gamma }}^{{\mathrm{qp}}}$) of possible quasi-particles are compactly expressed as an ordinary complex number $z_n^{{\mathrm{qp}}} = E^{{\mathrm{qp}}} - i{\mathrm{\Gamma }}^{{\mathrm{qp}}}$. Then the Dyson equation leads to a pair of coupled non-linear equations²¹,

$${z_n^{{\mathrm{qp}}} - \epsilon _j^{\mathbf{k}} - {\mathrm{\Sigma }}_{{\mathbf{k}}j}\left( {z_n^{{\mathrm{qp}}}} \right) = 0 \to \left\{ {\begin{array}{*{20}{l}} {E_n^{{\mathrm{qp}}} - \epsilon _j^{\mathbf{k}} - {\mathrm{Re}}\left( {{\mathrm{\Sigma }}_{{\mathbf{k}}j}\left( {E_n^{{\mathrm{qp}}} - i{\mathrm{\Gamma }}_n^{{\mathrm{qp}}}} \right)} \right)} \hfill & = \hfill & 0 \hfill \\ {{\mathrm{\Gamma }}_n^{{\mathrm{qp}}} + {\mathrm{Im}}\left( {{\mathrm{\Sigma }}_{{\mathbf{k}}j}\left( {E_n^{{\mathrm{qp}}} - i{\mathrm{\Gamma }}_n^{{\mathrm{qp}}}} \right)} \right)} \hfill & = \hfill & 0 \hfill \end{array}} \right\}}.$$

(1)

Capturing the influence of the quasi-particle lifetime broadening on its shifted energy and vice versa, as above, is not the most standard procedure but appears absolutely crucial when trying to understand the spectral features of many strongly interacting systems in terms of elementary excitations, as shall be the case also in MoS₂.

We have solved Eq. (1) for monolayer MoS₂, and the results are shown in Fig. 3e. For the sake of clarity, we focused on the same momentum region as in Fig. 3b, and only on the strongly interacting outer spin-split band. Close to the Fermi momentum k_F, an Engelsberg–Schrieffer-like³ state appears with a strongly renormalized dispersion, and it is denoted as the $n = 1$ solution. Far enough from k_F, we find a dispersive and damped state identified as the $n = 3$ solution. An important conclusion is that for some intermediate values of the momentum we find an additional solution ($n = 2$) with an important spectral weight which is practically flat, and it is therefore a strongly interacting state which tends to localization. However, this state appears long lived as it lies just in the energy window where the imaginary part of the self-energy has almost a gap (Fig. 3d). More specifically, the electron–phonon limited lifetime broadening at this energy range is almost negligible ${\mathrm{\Gamma }}_{n = 2}^{{\mathrm{qp}}} \sim 0.35\,{\mathrm{meV}}$. Considering the Dyson equation in the complex plane allows also to associate a precise spectral weight to each quasi-particle state, in a systematic way, and is simply given by the residue of the poles $\left( {{\Bbb Z}_n^{{\mathrm{qp}}} = 1/\left( {1 - {\mathrm{\Sigma }}\prime \left( {z_n^{{\mathrm{qp}}}} \right)} \right)} \right)$ evaluated at complex quasi-particle energies. It is not therefore necessary to visually analyze the spectral function $A(\omega )$ in order to check for the energies of possible quasi-particle states and/or their relative importance, as these are given directly by $z^{{\mathrm{qp}}}$ and ${\Bbb Z}_n^{{\mathrm{qp}}}$. This allows to define the coherent part of the spectral-function systematically $\left( {A^{{\mathrm{qp}}}({\mathbf{k}},\omega ) = - \mathop {\sum}\nolimits_n {{\kern 1pt} \frac{1}{\pi }{\kern 1pt} {\mathrm{Im}}\left( {\frac{{{\Bbb Z}_n^{{\mathrm{qp}}}({\mathbf{k}})}}{{\omega - z_n^{{\mathrm{qp}}}({\mathbf{k}})}}} \right)} } \right)$, and explicitly broken down into separate contributions from each quasi-particle pole. Note for a moment the severe consistency condition $\mathop {\sum}\nolimits_n {{\kern 1pt} {\mathrm{Re}}\left( {{\Bbb Z}_n} \right)} \lesssim 1$ imposed here as the integral of $A^{{\mathrm{qp}}}({\mathbf{k}},\omega )$ must be of the order but less than unity. Said in pass, this result is not obtained by any means when only the real part of the self-energy is considered for calculating the dispersion of quasi-particles (see Supplementary Note 2). When the contribution of each separate pole $A_{n = 1,3}^{{\mathrm{qp}}}({\mathbf{k}},\omega )$ is plotted as in Fig. 3f, the comparison with the full spectral function (Eq. (7) in Methods) in Fig. 3c is strikingly good. In this figure, it is also shown how strongly the spectral weight from one quasi-particle into others is transferred as a function of k, even when for some values of momentum all the three many-body solutions are present.

Discussion

Altogether, the obtained quasi-particle band structure—in its complex version—almost perfectly resembles the three-peak and double-gap structure observed in ARPES. Therefore, the threefold band structure observed in experiment corresponds certainly to quasi-particle states and not to multiple-phonon (high order) processes nor to side-bands or satellites without a clear physical meaning.

These findings provide a theoretical explanation for the singular spectral features observed on monolayer MoS₂¹² in terms of three elementary many-body quasi-particle states. Close to the ${\bar{\mathrm{K}}}$ valley, the available scattering phase-space appears severely restricted for some narrow energy windows, with the result that one quasi-particle branch ($n = 2$) appears exceptionally long lived, even when the strong coupling induces a practically flat dispersion for this band. Flat dispersion indicates a sort of real space localization property of these states and, therefore, the effective interactions between them should be expected to be profoundly modified. As the transport and superconducting properties^13,14,15,16 depend so dramatically on the lifetime, dispersion and effective interactions between elementary excitations, we believe that these results may serve as a guidance to understand, explore, and eventually take advantage of many-body interactions.

Methods

First-principles calculations

The first-principles calculations were performed within the noncollinear density functional theory (DFT)^22,23 and density functional perturbation theory (DFPT)²⁴ with fully relativistic norm-conserving pseudopotentials as implemented in the Quantum Espresso package²⁵ and using the Perdew–Zunger local density approximation parametrization for the exchange-correlation functional²⁶. In order to correctly describe the ground-state electronic and phononic structures of the single-layer MoS₂, we used the experimentally measured in-plane bulk lattice parameter a = 3.16 Ų⁷ and a vacuum layer of five times the lattice parameter, which is large enough for avoiding any interplay between adjacent layers. Carrier doping effects were simulated by the addition of excess electronic charge into the unit cell, which is compensated by a uniform positive jellium background. All atomic forces were relaxed up to at least 10⁻⁶ Ry $a_0^{ - 1}$. We used a 36 × 36 Monkhorst–Pack grid for the self-consistent electronic calculations, while the lattice vibrational properties were evaluated on a coarse 9 × 9 q-point mesh.

Electron–phonon interaction calculations

The self-consistent electron–phonon magnitudes were computed considering doping-sensitive full-spinor electron states, as well as doping-sensitive phonon states and deformation potentials. In a first step we considered a coarse mesh of 9 × 9 for phonons (q) and a 18 × 18 mesh for electron states (k), but for fine integrals, we used the Wannier interpolation scheme^28,29,30, which allowed us to consider 10⁷ points in the Brillouin zone for electrons and 10⁶ for phonons. The FS integrated squared matrix elements (Fig. 2c), equivalent to a sort of electron–phonon weighted nesting function defined for the phonon branch ν at q, is defined by the following integral:

$$\left\langle {\left| {g_\nu ^{\mathbf{q}}} \right|^2} \right\rangle _{{\mathrm{FS}}} = \frac{1}{{N(E_{\mathrm{F}})}}\mathop {\sum }\limits_{{\mathbf{k}}ij} \left| {g_{ij}^\nu ({\mathbf{k}},{\mathbf{q}})} \right|^2\delta \left( {\epsilon _j^{\mathbf{k}} - \epsilon _i^{{\mathbf{k}} + {\mathbf{q}}} \pm \omega _\nu ^{\mathbf{q}}} \right)\delta \left( {\epsilon _j^{\mathbf{k}} - E_{\mathrm{F}}} \right),$$

(2)

where $\epsilon _j^{\mathbf{k}}$ is the single-particle bare eigenvalue of the electron state with momentum k in the band j, $\omega _\nu ^{\mathbf{q}}$ is the frequency of the lattice vibrational normal mode with momentum q and mode ν, N(E_F) the DOS at E_F, and $g_{ij}^\nu ({\mathbf{k}},{\mathbf{q}})$ the electron–phonon matrix element connecting the |k, j〉 and |k + q, i〉 electron states by a phonon |q, ν〉. This quantity allows us to identify the relevant phonon modes interplaying with electrons at E_F and offers a measure of the strength of the coupling for each phonon mode |q, ν〉.

The mass enhancement parameter or FS averaged electron–phonon coupling strength is defined as²:

$$\lambda = \frac{1}{{N(E_{\mathrm{F}})}}\frac{1}{{N_q}}{\kern 1pt} \mathop {\sum }\limits_{{\mathbf{kq}}ij\nu } {\kern 1pt} \frac{{\left| {g_{ij}^\nu ({\mathbf{k}},{\mathbf{q}})} \right|^2}}{{\omega _\nu ^{\mathbf{q}}}}\delta \left( {\epsilon _j^{\mathbf{k}} - \epsilon _i^{{\mathbf{k}} + {\mathbf{q}}} \pm \omega _\nu ^{\mathbf{q}}} \right)\delta \left( {\epsilon _j^{\mathbf{k}} - E_{\mathrm{F}}} \right).$$

(3)

This factor reveals how much the effective mass is enhanced $m = m_0(1 + \lambda )$ at the Fermi level due to the electron–phonon interaction. The state |k, j〉 resolved electron–phonon coupling strength (Fig. 2d) was evaluated as:

$$\lambda _{{\mathbf{k}}j} = \frac{1}{{N_q}}{\kern 1pt} \mathop {\sum }\limits_{{\mathbf{q}}i\nu } {\kern 1pt} \frac{{\left| {g_{ij}^\nu ({\mathbf{k}},{\mathbf{q}})} \right|^2}}{{\omega _\nu ^{\mathbf{q}}}}\delta \left( {\epsilon _j^{\mathbf{k}} - \epsilon _i^{{\mathbf{k}} + {\mathbf{q}}} \pm \omega _\nu ^{\mathbf{q}}} \right).$$

(4)

The semi-empirical McMillan–Allen–Dynes formula for estimating the superconducting critical temperature T_c is defined as:

$$T_{\mathrm{c}} = \frac{{\omega _{{\it{log}}}}}{{1.2}}{\mathrm{exp}}\left( { - \frac{{1.04(1 + \lambda )}}{{\lambda - \mu ^ \ast (1 + 0.62\lambda )}}} \right),$$

(5)

where $\omega _{{\it{log}}}$ is a logarithmic average of the phonon frequencies and μ* is a parameter describing the Coulomb repulsion. We estimated the superconducting critical temperature of the doped monolayer MoS₂ for some values of μ* within the range of 0.1–0.3, obtaining values in the range of 4–8 K, with a calculated electron–phonon coupling of λ ~ 0.63. This estimation is in agreement with the experimentally measured critical temperature of 8.5 K at a 2D-carrier density $n_{2{\mathrm{D}}} = 9 \times 10^{13}\,{\mathrm{cm}}^{ - 2}$^13,14,15,16.

Electron self-energy and spectral function

The ab initio expression for the Fan–Migdal electron self-energy valid at T = 0 K used in our calculations was²⁸:

$${\mathrm{\Sigma }}_{{\mathbf{k}}j}(\omega ) = {\textstyle{1 \over {N_q}}}{\kern 1pt} \mathop {\sum }\limits_{{\mathbf{q}}i\nu } {\kern 1pt} \left| {g_{ij}^\nu ({\mathbf{k}},{\mathbf{q}})} \right|^2\left( {{\textstyle{{f\left( {\epsilon _i^{{\mathbf{k}} + {\mathbf{q}}}} \right)} \over {\omega - \epsilon _i^{{\mathbf{k}} + {\mathbf{q}}} + \omega _\nu ^{\mathbf{q}} + i\eta }}} + {\textstyle{{1 - f\left( {\epsilon _i^{{\mathbf{k}} + {\mathbf{q}}}} \right)} \over {\omega - \epsilon _i^{{\mathbf{k}} + {\mathbf{q}}} - \omega _\nu ^{\mathbf{q}} + i\eta }}}} \right),$$

(6)

where $\omega$ represents the quasi-particle energy in the real-energy axis, f denotes the Fermi-Dirac occupation factor, and η is a real positive infinitesimal. The electron self-energy as calculated in Eq. (6) allows to obtain the spectral function for real frequencies^1,2,28:

$$\begin{array}{*{20}{l}} {A({\mathbf{k}},\omega )} \hfill & = \hfill & { - {\textstyle{1 \over \pi }}{\kern 1pt} \mathop {\sum }\limits_j {\kern 1pt} {\mathrm{Im}}\left( {G({\mathbf{k}},\omega )} \right) = - {\textstyle{1 \over \pi }}{\kern 1pt} \mathop {\sum }\limits_j {\kern 1pt} {\mathrm{Im}}\left( {{\textstyle{1 \over {\left( {\omega - \epsilon _j^{\mathbf{k}} - {\mathrm{\Sigma }}_{{\mathbf{k}}j}(\omega )} \right)}}}} \right)} \hfill \\ {} \hfill & = \hfill & { - {\textstyle{1 \over \pi }}{\kern 1pt} \mathop {\sum }\limits_j {\kern 1pt} {\textstyle{{{\mathrm{Im}}\left( {{\mathrm{\Sigma }}_{{\mathbf{k}}j}(\omega )} \right)} \over {\left( {\omega - \epsilon _j^{\mathbf{k}} - {\mathrm{Re}}\left( {{\mathrm{\Sigma }}_{{\mathbf{k}}j}(\omega )} \right)} \right)^2 + \left( {{\mathrm{Im}}\left( {{\mathrm{\Sigma }}_{{\mathbf{k}}j}(\omega )} \right)} \right)^2}}}.} \hfill \end{array}$$

(7)

Analytic continuation of the electron self-energy

In order to find solutions of the complex quasi-particle equation (Eq. (1)), we need to perform an analytical continuation of the electron self-energy ${\mathrm{\Sigma }}(\omega )$ from the upper half complex plane into the lower half. First, we calculated the self-energy from first-principles only for real frequencies (Eq. (6)), and next we generalized the method outlined in ref. ²¹ to handle self-energies without assuming particle-hole symmetry. For doing so, we used the Kramers–Kronig relation integrated by parts,

$${\mathrm{\Sigma }}(\omega + i\delta ) = \mathop {\smallint }\limits_{ - \infty }^\infty {\kern 1pt} d\omega \prime \left. {\frac{{d{\kern 1pt} {\mathrm{Im}}\left( {{\mathrm{\Sigma }}(\omega \prime\prime )} \right)}}{{d\omega \prime\prime }}} \right|_{\omega \prime\prime = \omega \prime }{\kern 1pt} {\mathrm{log}}(\omega - \omega \prime + i\delta ).$$

(8)

As it is known, a direct substitution of $\omega$ by z in Eq. (8) is not valid, as the branch-cuts introduced by the log term makes the direct numerical integration inappropriate. However, a piecewise polynomial interpolation of $\frac{{d{\mathrm{Im}}({\mathrm{\Sigma }}(\omega ))}}{{d\omega }}$ and a subsequent analytical integration is a possible numerical strategy. We used a cubic spline interpolation, ensuring the continuity of the first and second derivatives all over the $\omega$ axis.