Abstract
While cumulative carbon dioxide (CO2) emissions dominate anthropogenic warming over centuries, temperatures over the coming decades are also strongly affected by short-lived climate pollutants (SLCPs), complicating the estimation of cumulative emission budgets for ambitious mitigation goals. Using conventional Global Warming Potentials (GWPs) to convert SLCPs to “CO2-equivalent” emissions misrepresents their impact on global temperature. Here we show that peak warming under a range of mitigation scenarios is determined by a linear combination of cumulative CO2 emissions to the time of peak warming and non-CO2 radiative forcing immediately prior to that time. This may be understood by expressing aggregate non-CO2 forcing as cumulative CO2 forcing-equivalent (CO2-fe) emissions. We show further that contributions to CO2-fe emissions are well approximated by a new usage of GWP, denoted GWP*, which relates cumulative CO2 emissions to date with the current rate of emission of SLCPs. GWP* accurately indicates the impact of emissions of both long-lived and short-lived pollutants on radiative forcing and temperatures over a wide range of timescales, including under ambitious mitigation when conventional GWPs fail. Measured by GWP*, implementing the Paris Agreement would reduce the expected rate of warming in 2030 by 28% relative to a No Policy scenario. Expressing mitigation efforts in terms of their impact on future cumulative emissions aggregated using GWP* would relate them directly to contributions to future warming, better informing both burden-sharing discussions and long-term policies and measures in pursuit of ambitious global temperature goals.
Similar content being viewed by others
Introduction
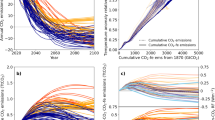
The Paris Agreement introduced a regular (5-yearly) “stocktake” of collective progress towards achieving its long-term temperature goals, but the metrics of progress to be used in these stocktakes remain under discussion.1,2,3,4,5,6,7,8,9 Relating emissions to future temperatures remains ambiguous as long as contributions are expressed, as in the majority of “Nationally Determined Contributions” (NDCs), in terms of CO2-equivalent (CO2-e) emission rates in a specific year defined using a metric such as the 100-year Global Warming Potential (GWP100). Figure 1a shows peak warming in scenarios10 considered by Working Group 3 of the IPCC 5th Assessment Report (AR5—colors represent scenarios categorized by 2100 CO2-equivalent radiative forcing,11 under the median climate response of the MAGICC simple climate model,12 plotted against 2030 CO2-e emissions conventionally calculated using AR5 GWP100 values. The two variables are positively correlated, but peak warming also depends on scenario-dependent assumptions about emissions after 2030. Most of these scenarios extrapolate the implications of short-term commitments using some notion of “sustained ambition”, interpreted in a number of ways, including13 an effective global carbon price increasing at a constant exponential rate over the 21st century. Despite having some idealized economic justification, this may not coincide with many non-specialists’ expectations of “sustained effort”. Hence the conventional approach to assessing whether a medium-term emissions trajectory is consistent with a long-term temperature goal, simply by comparing it with a set of available scenarios, is opaque at best, and at worst misleading. Moreover, the correlation in Fig. 1a is weakest within the most ambitious (light blue) scenario family, reflecting the greater fractional contributions of non-CO2 forcing agents to peak warming in scenarios with the lowest cumulative stock of CO2 emissions.
Temperature change for the median climate response12 to a subset of the IPCC AR5 scenario database plotted against a total CO2-equivalent emissions in 2030 computed using GWP100; b cumulative CO2-e emissions; c cumulative CO2 emissions to the time of peak warming excluding (large dots) and including (small dots) an empirical correction for non-CO2 forcing and d cumulative CO2-forcing-equivalent emissions. Gray lines in b–d show TCRE values of 1, 1.5, 2 and 2.5 °C/TtC. Black line in d shows warming as a function of cumulative CO2 emissions in a simulation forced11 with CO2 emissions only from the RCP2.6 scenario. a, c show peak warming while b and d show temperature evolution, both relative to 2005, in each scenario
The relationship between cumulative CO2 emissions and CO2-induced warming provides a simple, scenario-independent, approach to assessing the implications of future CO2 emissions, but the concept of an “emissions budget” cannot be extended to CO2-e emissions as conventionally calculated. Figure 1b shows trajectories of future warming plotted against cumulative CO2-e emissions based on GWP100. The correlation is stronger than in Fig. 1a, but breaks down as scenarios approach peak warming; the four most ambitious 430–480 ppm scenarios show almost 1000 GtCO2-e emitted after temperatures have largely stabilised. These figures show that cumulative CO2-e emissions calculated using GWP100 are a poor indicator of peak warming, and CO2-e emission rates are a poor indicator of temperature stabilisation.
This paper explores an alternative approach to quantifying the contribution of non-CO2 emissions to future temperatures, focussing on the kind of ambitious mitigation scenario that will be required if the goals of the Paris Agreement are to be met. It will also show how such an approach can be used to quantify the contribution of individual regions to future temperature change.
Context: alternatives to conventional CO2-equivalent emissions
The concept of CO2-e emissions is deeply embedded in climate policy14 despite long-standing criticisms15 of its application to SLCPs when constructed using GWP100. Ambiguity arises because emissions of cumulative pollutants and SLCPs translate into impact on the planetary energy budget in fundamentally different ways: for cumulative pollutants like CO2, radiative forcing largely scales with the total stock (cumulative integral) of emissions to date, while for SLCPs like methane, it scales with the current flow (emission rate) multiplied by the SLCP lifetime.4,5,16,17 The differing climate impacts of CO2 and SLCP emissions become particularly problematic under ambitious mitigation. Falling SLCP emissions lead to falling global temperatures, while nominally “equivalent” CO2 emissions, whether computed using GWP, global temperature-change potential (GTP),4,14 or any other conventional metric, would incorrectly suggest that these falling emissions would cause further warming. As well as being misleading, using GWP to calculate CO2-equivalent emissions has practical consequences: if “balance” is defined as net zero CO2-e emissions, balanced emissions result not in temperature stabilisation, but an indefinite cooling trend, with the rate of cooling determined by on-going emissions of SLCPs.18
Figure 1c shows a more physically-based approach. Large dots show peak warming plotted against cumulative CO2 emissions to the time of peak warming: there is a positive relationship, but with a large residual spread (0.13 °C standard deviation, or s.d., about the best-fit line). Small dots show that almost all of this spread can be accounted for by differences in non-CO2 forcing between the different scenarios. They show peak warming plotted against a linear combination of cumulative CO2 emissions to the time of peak warming and average non-CO2 forcing over the 20 years prior to the time of peak warming (so assuming temperatures at the time of peak warming have adjusted to this forcing), with an empirically-estimated conversion factor of 1274 GtCO2/(W/m2). This leaves only a small unexplained residual (s.d. of 0.021 °C) across these scenarios. By contrast, if cumulative CO2-e emissions computed using conventional GWPs are used to predict peak warming, as in Fig. 1b, the residual is significantly larger (s.d. of 0.052 °C). Hence cumulative emission budgets can be a useful and accurate tool for predicting peak warming under ambitious mitigation, but only if non-CO2 forcings are accurately accounted for.
Genuinely equivalent emission pathways (in terms of their impact on global temperatures over the full range of timescales) can be derived by expressing a radiative forcing pathway as a CO2-equivalent concentration pathway and then diagnosing the CO2 forcing-equivalent (CO2-fe) emissions19 that would yield that concentration pathway using a carbon cycle model20 (see Methods). By construction, these CO2-fe emissions give the same radiative forcing pathway and hence temperature response21 as the corresponding forcing agent(s) from which they are computed.22 In Fig. 1d we observe the same linear, scenario-independent relationship between total human-induced warming and total cumulative CO2-fe emissions (computed from all anthropogenic climate forcing agents, including aerosols) as is observed between CO2-induced warming and cumulative CO2 emissions in this version of the MAGICC model driven with the RCP2.6 scenario (black line). For reference, the gray lines in Fig. 1b–d show isolines of Transient Climate Response to Emissions, or TCRE: this model displays a TCRE of 1.69 °C/TtC for the 1000 GtCO2 emitted after 2005, in approximate agreement with the slope of 1.83 °C/TtC for the small dots in Fig. 1c. Remaining discrepancies likely result from different temperature responses to different forcings in the MAGICC model (only total forcings, not effective radiative forcings,14 are available for these scenarios, although a simple correction is applied to account for aerosol efficacy, see Methods) and the transition from concentrations-driven to emissions-driven integration after 2005.23 Figure 1d shows that, in multi-gas scenarios, temperatures stabilise when and only when the annual net rate of total anthropogenic CO2-fe emissions reaches zero, which is not the case for either CO2 emissions alone or CO2-e emissions computed using GWP.
CO2-fe emissions depend on knowledge of the full scenario history and must be computed using a carbon cycle model, and so would be difficult to use directly as an emission metric. However, because they provide climatically equivalent emissions by construction, they represent a standard against which other emission metrics can be judged. Reference3 showed that a new usage of the conventional GWP approximates the relative impact of both cumulative pollutants and SLCPs on global temperatures under some idealized scenarios. This usage, which we denote GWP*, considers a sustained one-tonne-per-year increase in the emission rate of an SLCP (as introduced by refs.4,5) to be equivalent (in terms of temperature impact) to a one-off pulse emission of \({\mathrm{GWP}}_H \times H\) tonnes of CO2 (denoted CO2-e*), where \({\mathrm{GWP}}_H\) is the value of that SLCP’s GWP for a time-horizon \(H\). Here we add the additional refinement that the pulse emission is spread over 20 years following the increase in the SLCP emission rate: this reduces the volatility of CO2-e* emissions in response to variations in SLCP emission rates, and better reflects the temperature impact of SLCPs. For pollutants with lifetimes longer than \(H\), like nitrous oxide (N2O), GWP-based CO2-e and CO2-e* are identical.
CO2-e* emissions can also be calculated directly from radiative forcing, which is useful for species such as aerosols for which trends in radiative forcing are better characterized than either emissions or lifetimes: a permanent unit increase in radiative forcing can be considered equivalent to an emission of \(H/{\mathrm{AGWP}}_{H-(\mathrm{CO}_2)}\) tonnes of CO2 distributed over the 20 years following the forcing increase, where \({\mathrm{AGWP}}_{H(\mathrm{CO}_2)}\) is the Absolute Global Warming Potential4 of CO2 over time-horizon \(H\) appropriate to these scenarios (see Methods). Hence we expect peak warming relative to the present to be given by
where \(G_{{\mathrm{CO2}}}\) is cumulative CO2 emissions from now to the time of peak warming and \(\Delta F_{{\mathrm{non - CO2}}}\) the change in non-CO2 forcing between 20 years prior to the present and 20 years prior to the time of peak warming. The small constant term (only −0.02 °C in this set of scenarios) reflects any systematic response to forcing outside this period. Thus, the empirical correction represented by the difference between the small and large dots in Fig. 1c is, in effect, an estimate of the factor \(H/{\mathrm{AGWP}}_{H(\mathrm{CO}_2)}\), which is model-dependent and scenario-dependent.24 Injection of CO2 into this version of the MAGICC model (see Methods) indicates a value of 1216 GtCO2/(W/m2), in good agreement with the empirical estimate. AGWP100 values from AR5 indicate14 a central value of 1091 GtCO2/(W/m2), with a range of 866–1474 GtCO2/(W/m2) reflecting a variety of carbon cycle models, encompassing other recent estimates.25
Results
Using GWP* in the analysis of ambitious mitigation scenarios
The advantages of GWP* over GWP under ambitious mitigation are even more apparent when we consider individual contributions to warming. Figure2 shows historical emissions9,14 and projected changes from 2015 following an ambitious mitigation scenario23 (RCP2.6) expressed as CO2-e (top) and CO2-e* (bottom). Left panels show annual emission rates, and right panels show cumulative (integrated) emissions. CO2-e and CO2-e* emissions of CO2 and N2O are identical, but annual CO2-e* methane emissions (Fig. 2c) track the rate of change of methane emissions, unlike CO2-e (Fig. 2a), which track methane emissions themselves. Hence methane CO2-e* emissions rose rapidly in the 1950s and fell over the 1990s as the rate of increase in methane emissions stalled. They have since recovered but are projected to soon become negative (falling actual methane emissions) under RCP2.6. CO2-e* emissions of other SLCPs (primarily aerosols, but also including the impact of tropospheric ozone) follow an opposite path, but change sign earlier. Radiative forcing due to aerosols and ozone is estimated to have been almost constant over the past 20 years (giving near-zero current CO2-e* emissions of SLCPs other than methane), while methane emissions have risen: hence the current decade is experiencing a uniquely high positive contribution to total CO2-e* emissions (the difference between the orange and black lines in Fig. 2c from the combined effects of recent methane, aerosol and ozone trends.
Annual a, c and cumulative b, d CO2-e and CO2-e* emissions under the GWP100 a, b and GWP* c, d metrics using historical emissions to 2015 extended with the RCP2.6 scenario. Dashed lines show global mean surface temperature (GMST) response to radiative forcings associated with these emissions (not available separately for land-use CO2). Colors indicate gases following the legend in a, with “Aerosol” also including ozone and other minor constituents. Thin solid lines in d show cumulative CO2-forcing-equivalent emissions closely tracking GMST response
The greater “environmental integrity” of the GWP* metric (meaning, in the UNFCCC context,26 its fitness-for-purpose as a metric of progress towards a global-temperature-related climate goal) is evident comparing cumulative CO2-e and CO2-e* emissions in Fig. 2b, d with global temperature responses (dashed lines and right axes) and CO2-fe emissions (thin lines in 2d), both diagnosed from the associated radiative forcing timeseries.23 Cumulative CO2-e* emissions closely track both cumulative CO2-fe emissions and resulting temperature changes (Fig. 2d), while GWP100-based CO2-e performs poorly for SLCPs, particularly when emissions are falling (Fig. 2b—see especially the divergence between the orange dashed and solid lines after 2050, and between blue and purple dashed and solid lines from 2000 onwards). Adopting another conventional time-invariant metric such as GWP20 or a GTP would simply scale up or scale down the methane and aerosol CO2-e emissions in Fig. 2b, making no difference to their poor temporal correspondence with CO2-fe emissions or temperature responses. Even a time-dependent GTP17 would still equate a falling rate of emission of an SLCP with a continued positive emission of CO2.
It is important to note that, despite corresponding to zero CO2-e*, a constant on-going high level of SLCP emissions may still represent an important contribution to warming to date and/or a mitigation opportunity. Negative CO2-e* emissions become possible through reducing SLCP emission rates: a policy intervention that permanently reduces an SLCP emission rate corresponds, in terms of its impact on future temperatures, to active removal of a given amount of CO2. Active CO2 removal may become increasingly important under ambitious mitigation, making it all the more important for metrics to relate it realistically to other measures.
Since cumulative CO2-e* emissions based on GWP* provide a relatively unambiguous indication of future warming, CO2-e* emission rates indicate future warming rates. This makes it clear what the commitments made in the Paris Agreement actually promise: they directly determine the rate of human-induced warming in 2030 due to gases covered by the agreement. Assuming nationally determined contribution (NDC) goals are met, and using the breakdown of emissions provided by ref. 8 (many countries do not specify this in their NDCs), combined CO2, methane and nitrous oxide emissions in 2030 are 28% lower than in a “Reference-No Policy” scenario if measured by GWP*. Because of the unambiguous relationship between CO2-e* emissions and future temperatures, this equates to a 28% reduction in the rate of warming caused by these gases in 2030; the same NDCs correspond to an 18% reduction in CO2-e emission based on GWP100, but there is no unambiguous way of relating this to future temperatures.
Using GWP* to quantify regional contributions to global temperature change
In addition to assessing the implications of future policies, emission metrics can also be used to assess countries’ or regions’ contributions to changes in global average temperature. Figure 3 shows emissions from different regions (defined in the ref. 9) either in 2010–2014 (left panels), or from 1870 to 2012 (right panels), computed using the metrics from the corresponding panels of Fig. 2, all plotted against the model-estimated contribution to warming to date relative to pre-industrial (or, in Fig. 3c, current warming rate), which we simulate (see Methods) using emissions from that region alone, setting emissions in all other regions to zero. The solid diagonal line in each panel shows the ratio of global temperature rise (or warming rate in Fig. 3c) to aggregate global emissions under each metric: in the absence of non-linearity, with a single greenhouse gas and identical time-histories of emissions in all regions, all points would lie on this line. How close points are to a straight line is an indication of the accuracy of different greenhouse gas metrics as indicators of warming given diverse regional emissions time-histories and the mix of CO2 and SLCPs emitted.
Annual (left: 2010-2014 average) and cumulative (right: from 1751 to 2012) CO2-equivalent emissions under the GWP and GWP* metrics for selected regions, compared with the contributions of emissions from these regions to global temperature rise to 2012 (a, b, and d) and the rate of global temperature rise 2010–2014 (c) estimated using a simple climate model; see Methods. Solid diagonal lines show ratio of total global temperature rise (or rate of rise in c) to total global emissions under the metric shown. Dotted lines show best-fit regression lines under a logarithmic fit, with residuals about these lines given as root-mean-square fractional prediction errors. e, f Compare annual rates of emissions and cumulative emissions, respectively, under the two different metrics
Annual GWP100-based emissions (Fig. 3a) are a relatively poor indicator of regional contributions to warming, although often used in discussions of burden sharing: the root-mean-square fractional prediction error (FPE—see Methods) is over 36%. Cumulative GWP100-based emissions (Fig. 3b) perform better, largely because many regions’ historical emissions are dominated by CO2, but the FPE is still over 9%. Cumulative emissions based on GWP* Fig. 3d) provide a very accurate indication of relative contributions to warming, with an FPE of only 2%. While Fig. 3b, d provide a like-for-like comparison, Figure 3c shows, for comparison, that annual emission rates computed using GWP* also provide a reasonably accurate prediction of contributions to current warming rates (FPE of 9%, but of a much noisier quantity): if computed using GWP (not shown, but visually similar to Fig. 3a) the FPE in warming rates increases to over 30%. GWP could even predict contributions to warming rates of the wrong sign under falling SLCP emissions: hence problems with the use of GWP to compare regions’ contributions will intensify as more regions undertake ambitious SLCP mitigation. Figure 3e, f show regions’ annual and cumulative emissions calculated with GWP100 and GWP* plotted against each other, with diagonal lines showing corresponding ratios of global emissions. Regions above the line in 3e would show a nominal fall in their annual emissions (relative to the global total) if recalculated using GWP* rather than GWP100. These are typically regions with high but falling SLCP emissions over the 20 years preceding 2012. Agreement between cumulative emissions under the two metrics is much better, reflecting the fact that these are dominated by CO2 in many regions.
Parties to the UNFCCC have considerable latitude in how they arrive at their NDCs, but given that the long-term goals of the Paris Agreement are expressed in terms of global temperature, a more consistent alignment of NDCs with the long-term temperature goal might clarify their implications in any stocktake mechanism. A region’s contribution to total future warming by any given date is simply its total cumulative CO2-e* emissions, computed with GWP*, between now and that time, multiplied by the TCRE.27,28 Hence GWP* provides a way of applying the TCRE, a useful summary metric of climate response and the uncertainties therein, also to gases other than CO2.
Discussion
The importance of cumulative CO2 emissions has long been recognised,15,17,19,25,29 but climate policy has continued to focus on CO2-e emission rates because cumulative budgets have been thought to apply only to CO2. Relating emissions using GWP* allows all emissions to be considered in a common cumulative framework. CO2-e* emissions closely approximate CO2-fe emissions, which behave (by construction) exactly like CO2. Formulating NDCs and, perhaps even more important, “mid-century, long-term low greenhouse gas emission development strategies”,25 in terms of cumulative CO2-e* emissions would provide a more accurate indication of progress towards climate stabilisation.30 While shorter-term goals for emission rates of individual gases and broader metrics encompassing emissions’ co-impacts2,6,31 remain potentially useful in defining how cumulative contributions will be achieved, summarising commitments using a metric that accurately reflects their contributions to future warming would provide greater transparency in the implications of global climate agreements as well as enabling fairer and more effective design of domestic policies and measures. Policies drawing on GWP* could thus be a useful step towards reducing ambiguity in outcomes and ultimately implementing mitigation strategies for meeting the global goals of the Paris Agreement.
Methods
Methods and sources used in constructing Figs. 1, 2 and 3
Emissions and temperature responses in Fig. 1 are drawn directly from the IPCC AR5 scenarios provided on the IIASA database.10,13,32 The calculations for CO2-e and CO2-e* emissions use GWP100 values of 28 (39% uncertainty) for CH4, 265 (29% uncertainty) for N2O, and 9.17 × 10-14 W m-2 year kg-1 (26% uncertainty) for AGWP100(CO2), taken from ref. 14 Small dots in Fig. 1c show peak warming plotted against cumulative CO2 emissions empirically adjusted using the term in parenthesis in the model
with the parameters \(a_i\) estimated using an ordinary least-squares fit. The change in non-CO2 radiative forcing (ΔFnon-CO2) was calculated using radiative forcings from the IIASA database, with 1986–2005 forcing from the RCP8.5 historical forcing. Since only total forcings are available in the IIASA database, non-Kyoto-gas anthropogenic forcing is multiplied by a time-invariant scaling factor of 1.4 such that ensemble average scenario forcing reproduces observed14 aerosol ERF in the first year of the scenarios, 2005.
Emissions in Fig. 2 use historical data9 to 2015, extended with diagnosed emissions23 for the RCP2.6 scenario scaled to match the historical series in 2015. Aerosol and other forcing uses the RCP2.6 series scaled to reproduce the estimate of total anthropogenic forcing in 2011 given in ref. 14 Annual emissions and forcing are smoothed with a 5-year running mean before computing CO2-e, CO2-e* and CO2-fe emissions. Temperatures in Fig. 2 are computed directly from radiative forcing using a 2-time-constant climate response33 with an equilibrium climate sensitivity of 3 °C and transient climate response of 1.8 °C, matching the median behavior of the CMIP5 ensemble.
The agreement between cumulative CO2-equivalent methane emissions under GWP* and methane-induced warming in Fig. 1d might be further improved by including a small contribution that scales with time-integrated methane emissions. This could be justified by carbon cycle feedbacks34,35 and the oxidation of methane (from fossil sources) to CO2, but a composite metric would require more parameters, and precise agreement would depend on uncertain details of the climate response.
Temperatures in Fig. 3 are computed from regional emissions using a simple carbon cycle climate model that allows for changing airborne fraction in response to cumulative emissions and warming,24 and single lifetime models and standard formulae14 for radiative forcing for methane and N2O. Lifetimes of methane and N2O in this calculation only are adjusted to ensure global emissions result in observed concentration increase to 2011 (8.3 and 100 years, respectively). For these small warming levels, the impact of non-linearity in the response to CO2 is small but appreciable: the warming response to global emissions is 8% lower than the total of the warming responses to individual regions’ emissions, but the impact on relative contributions is negligible.9 Best-fit lines (dotted) in Fig. 3 are computed by a linear regression between the logarithms of the quantities plotted, with RMS fractional prediction errors expressed as \(100 \times \left( {\exp \left( {\sqrt {\chi ^2/\left( {n - 1} \right)} } \right) - 1} \right)\)%, where \(\chi ^2\) is the sum of the squared residuals of the logarithmic fit and \(n\) is the number of scenarios or regions.
Further details on the derivation of CO2 equivalent emissions using different metrics
GWP is defined as the Absolute GWP (AGWP) for a given climate forcing agent (the radiative forcing due to a pulse emission of that agent integrated over a time-horizon \(H\)) divided by the AGWP of CO2. Conventional CO2-e emissions for an SLCP are defined simply as emissions multiplied by the GWP: \(E_{{\mathrm{CO}}_2e} = E_{{\mathrm{SLCP}}} \times {\mathrm{GWP}}_H\)
Under GWP*, the time-integral of the rate of change of SLCP emissions over any given time period, or equivalently the change in SLCP emission rates between the beginning and end of that period, multiplied by \({\mathrm{GWP}}_H \times H\), gives total CO2-e* emissions over that period. This contrasts with the conventional use of GWP, under which CO2-e emissions are given by the time integral of the SLCP emissions themselves, multiplied by \({\mathrm{GWP}}_H\). Hence the rate of CO2-e* emissions under GWP* is defined for SLCP emissions by
and for radiative forcing by
where \(\Delta E_{{\mathrm{SLCP}}}\) and \(\Delta F\) are the change in SLCP emission rate or forcing over the preceding time-interval \(\Delta t\) (20 years in the examples here), \({\mathrm{GWP}}_H\) is the SLCP GWP and \({\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) is the Absolute GWP (AGWP) for CO2, both for time-horizon \(H\). For example, the annual rate of CO2-e* emissions for an SLCP in 2030 is the difference between the SLCP emission rate in 2030 and that in 2010 multiplied by \({\mathrm{GWP}}_H \times H/20\), while cumulative CO2-e* emissions to date for a particular SLCP are simply the average SLCP emission rate over the past 20 years multiplied by \({\mathrm{GWP}}_H \times H\). Conversely, a permanent 1 tonne-per-year change in emission rate of an SLCP in 2010 is equated to the emission of \(1/\left( {{\mathrm{GWP}}_H \times H} \right)\) tonnes of CO2-e* spread over the years 2010–2030.
A linear forcing increase of 1 W/m2 between the periods 1990-2010 and 2050-2070 equates to a total emission of \(H/{\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) tonnes of CO2-e* following a trapezoidal emission profile, increasing linearly from 2010 to 2030, then constant to 2050 and declining linearly to 2070.36 Injection of additional CO2 following this profile into this version of the MAGICC model gives a directly-estimated value for \(H/{\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) of 1216 GtCO2/(W/m2) for the total amount of CO2 required to increase average radiative forcing over the period 2050–2070 relative to 1990–2010. Modeling discontinuous changes in radiative forcing using CO2-e* would require infinite emission rates (just as it would require an infinite rate of emission of CO2 to give a discontinuous change in CO2-induced forcing).
Hence, under GWP*, a steadily declining rate of emission of an SLCP becomes equivalent to a negative sustained rate of emission of CO2-e*; likewise, a constant rate of SLCP emission equates to zero CO2-e*. This mimics the behavior of corresponding temperature responses: declining SLCP emissions reduce temperatures, while constant SLCP emissions cause no further warming. GWP or any other conventional metric treats these SLCP emissions as equivalent to continued positive emissions of CO2.
In defining CO2-e and CO2-e* emissions, we use \(H = 100\) years following established practice. Results under GWP* are insensitive to this provided \(H\) is much greater than the lifetime of the SLCP because the absolute GWP of an SLCP becomes a constant at these timescales, while the \({\mathrm{AGWP}}_H\) of the reference gas, CO2, increases linearly with \(H\)—see ref. 3 and Fig. 8.29 of ref. 14 Hence the \(H\)-dependence cancels out in the calculation of CO2-e* for both SCLP emissions and radiative forcing. In contrast, GWP-based CO2-e values for SLCPs scale approximately with \(1/H\), making the nominal relative importance of SLCPs and cumulative pollutants acutely sensitive to this choice of time-horizon. For completeness, aerosols and tropospheric ozone are shown as CO2-e emissions in Fig. 2a by dividing combined aerosol and ozone forcing by the AGWP100 of CO2, although as Fig. 2b demonstrates, this does not correspond to a geophysical quantity.
We use a simple 20-year difference (\({\mathrm{\Delta }}t\) in the above equations) to define rates of change of SLCP emissions, corresponding to the longest timescale over which emission policies are typically set: using a shorter \({\mathrm{\Delta }}t\) affects the variance of annual CO2-e* emission rates, but has no impact on cumulative CO2-e*. This introduces an average 10-year lag between changes in SLCP emission rates and their associated CO2-e* emissions, consistent with Fig. 2b of ref. 3 which shows that global temperatures take at least a decade longer to respond to a step-change in SLCP emission rates than to a pulse injection of CO237 because of the short-term response of the carbon cycle.32
A further consequence of the linear relationship between \({\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) and \(H\), combined with that between warming \(\Delta T\) and forcing increase \(\Delta F\) over a multi-decade time-period,38 is that the TCRE, or ratio26,27 of CO2-induced warming to cumulative CO2 emissions \(E\), is given by
where TCR is the Transient Climate Response, or the (non-equilibrium) warming at the time forcing reaches \(F_{{\mathrm{2x}}}\), the equivalent of doubling CO2 concentrations. The \({\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) and \(F_{{\mathrm{2x}}}\) values given in ref. 14 corresponding to early 21st-century conditions, imply TCRE = 0.9TCR per PgC, consistent with the overall IPCC assessment of TCRE and TCR.39 Climate models indicate40 the TCR is expected to increase under high forcing, while \({\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) may decrease24 due to the logarithmic relationship between forcing and CO2 concentration, partially compensated for by increasing CO2 airborne fraction.41 In the model used here, the \({\mathrm{AGWP}}_{H({\mathrm{CO}}_2)}\) decline dominates, such that CO2 emissions rise somewhat faster than CO2-induced warming after 2050 under a high (RCP8.5) emissions scenario. This decline in the TCRE under high emissions is not reflected in all models42 and is not relevant to the issue of GHG equivalence under ambitious mitigation.
CO2-fe emissions are diagnosed from radiative forcing timeseries by converting radiative forcing into CO2-equivalent concentrations, and then diagnosing the emissions required to give that concentration pathway using a carbon cycle model, in exactly the same way the CO2 emissions are routinely diagnosed from CO2 concentrations.23 The carbon cycle model used (FAIR)32 was parameterized using the following values to calculate the 100-year integrated impulse response function, \({\mathrm{iIRF}}_{100} = r_0 + r_cC_{{\mathrm{acc}}} + r_TT\); where \(r_0 = 33.6\,{\mathrm{years}};r_c = 0.0206\,{\mathrm{years}}\,{\mathrm{GtC}}^{ - 1};r_T = 4.635\,{\mathrm{years}}\,K^{ - 1}\), \(C_{{\mathrm{acc}}}\) is the accumulated perturbation carbon stock in the land and ocean and T is the global mean temperature anomaly relative to the preindustrial period. Parameters were chosen to maximize the agreement between cumulative CO2 emissions in MAGICC for the AR5 scenarios and those derived by inverting radiative forcing from MAGICC using the FAIR model. Full details of the FAIR model can be found in ref. 32
Differential radiative forcing efficacies and responses43 could be taken into account in this definition, although we use AR5 values throughout because only total radiative forcing is available for the MAGICC scenarios. The absolute magnitudes of CO2-fe emissions are affected by climate and carbon cycle uncertainties, but not their relative magnitudes or evolution over time.44
Data availability statement
All emission scenario and forcing datasets are downloaded from their respective websites. The FAIR model used in Figs. 2 and 3 is are available on https://github.com/OMS-NetZero/FAIR. The code and data used to produce Fig. 1 is available on https://gitlab.ouce.ox.ac.uk/OMP_climate_pollutants/gwpstar.git.
References
Rogelj, J. et al. Paris agreement climate proposals need a boost to keep warming well below 2 °C. Nature 534, 631–639 (2016).
Ocko, I. B. et al. Unmask temporal trade-offs in climate policy debates. Science 356, 492–493 (2017).
Allen, M. R. et al. A new use of Global Warming potentials to compare cumulative and short-lived climate pollutants. Nat. Clim. Change 6, 773–776 (2016).
Shine, K., Fuglestvedt, J., Hailemariam, K. & Stuber, N. Alternatives to the global warming potential for comparing climate impacts of emissions of greenhouse gases. Clim. Change 68, 281–302 (2005).
Lauder, A. R. et al. Offsetting methane emissions—an alternative to emission equivalence metrics. Int. J. Greenh. Gas Control 12, 419–429 (2013).
Shindell, D. et al. Simultaneously mitigating near-term climate change and improving human health and food security. Science 335, 183–189 (2012).
Shine, K. P., Berntsen, T. K., Fuglestvedt, J. S., Skeie, R. B. & Stuber, N. Comparing the climatic effects of emissions of short- and long-lived climate agents. Philos. Trans. R. Soc. A. 365, 1903–1914 (2007).
Fawcett, A. A. et al. Can Paris pledges avert severe climate change? Science 350, 1168–1169 (2015).
Skeie, R. B. et al. Perspective has a strong effect on the calculation of historical contributions to global warming. Environ. Res. Lett. 12, 024022 (2017).
Clark, L. et al. Assessing transformation pathways. in Edenhofer, O. et al (eds.) Climate Change 2014: Mitigation of Climate Change, Contribution of IPCC Working Group III to AR5 (eds, Edenhofer, O. et al) (Cambridge University Press, Cambridge, 2014).
Krey, V. et al. Annex 2—metrics and methodology. in Climate Change 2014: Mitigation of Climate Change. Contribution of IPCC Working Group III to AR5 (eds, Edenhofer, O. et al) (Cambridge University Press, Cambridge, 2014).
Meinshausen, M., Raper, S. C. B. & Wigley, T. M. L. Emulating coupled atmosphere-ocean and carbon cycle models with a simpler model, MAGICC6—part 1: model description and calibration. Atmos. Chem. Phys. 11, 1417–1456 (2011).
Kriegler, E. et al. Making or breaking climate targets: The AMPERE study on staged accession scenarios for climate policy. Technol. Forecast. Social Change 90A, 24–44 (2015).
Myhre, G. et al. Anthropogenic and natural radiative forcing. in Climate Change 2013: The Physical Science Basis (eds Stocker, T. F. & Qin, D. et al.) Ch. 8 (Cambridge University Press, Cambridge, 2013).
Pierrehumbert, R. T. Short-lived climate pollution. Ann. Rev. Earth Planet. Sci. 42, 341–379 (2014).
Smith, S. M. et al. Equivalence of greenhouse-gas emissions for peak temperature limits. Nat. Clim. Change 2, 535–538 (2012).
Reisinger, A., Havlik, P., Riahi, K. & Herrero, M. Implications of alternative metrics for global mitigation costs and greenhouse gas emissions from agriculture. Clim. Change 117, 677–690 (2013).
Fuglestvedt, J. S. et al. Implications of possible interpretations of “greenhouse gas balance” in the Paris agreement. Philos. Trans. R. Soc. A. https://doi.org/10.1098/rsta.2016.0445 (2018).
Zickfeld, K., Eby, M., Matthews, H. D. & Weaver, A. J. Setting cumulative emissions targets to reduce the risk of dangerous climate change. Proc. Natl Acad. Sci. 106, 16129–16134 (2009).
Wigley, T. M. L. The Kyoto protocol: CO2, CH4 and climate implications. Geophys. Res. Lett. 25, 2285–2288 (1998).
Tanaka, K. et al. Evaluating Global Warming potentials with historical temperature. Clim. Change 96, 443–466 (2009).
Manning, M. & Reisinger, A. Broader perspectives for comparing different greenhouse gases. Philos. Trans. R. Soc. A 369, 1891–1905 (2011).
Meinshausen, M. et al. The RCP greenhouse gas concentrations and their extension from 1765 to 2300. Clim. Change 109, 213 (2011).
Reisinger, A. M., Meinshausen, M. & Manning, M. Future changes in Global Warming potentials under representative concentration pathways. Environ. Res. Lett. 6, 024020 (2011).
Sterner, A. O. & Johansson, D. J. A. Effects of climate-carbon feedbacks on emission metrics. Environ. Res. Lett. 12, 034019 (2017).
UNFCCC, Adoption of the Paris Agreement, FCCC/CP/2015/10/Add.1, Article 4.13: https://unfccc.int/resource/docs/2015/cop21/eng/10a01.pdf (2015).
Matthews, H. D., Gillett, N. P., Stott, P. A. & Zickfeld, K. The proportionality of global warming to cumulative carbon emissions. Nature 459, 829–832 (2009).
Gillett, N. P., Arora, V. K., Matthews, D. & Allen, M. R. Constraining the ratio of global warming to cumulative CO2 emissions using CMIP5 simulations. J. Clim. 26, 6844–6858 (2013).
Allen, M. R. et al. Warming caused by cumulative carbon emissions towards the trillionth tonne. Nature 458, 1163–1166 (2009).
Bowerman, N. H. A. et al. The role of short-lived climate pollutants in meeting temperature goals. Nat. Clim. Change 3, 1021–1024 (2013).
Shindell, D. et al. A climate policy pathway for near- and long-term benefits. Science 356, 493–494 (2017).
IAMC AR5 Scenario Database: https://secure.iiasa.ac.at/web-apps/ene/AR5DB (2014).
Millar, R. J., Nicholls, Z. R., Friedlingstein, P. & Allen, M. R. A modified impulse-response representation of the global near-surface air temperature and atmospheric concentration response to carbon dioxide emissions. Atmos. Chem. Phys. 17, 7213–7228 (2017).
Gillett, N. P. & Matthews, H. D. Accounting for carbon cycle feedbacks in a comparison of the global warming effects of greenhouse gases. Environ. Res. Lett. 5, 034011 (2010).
Gasser, T. et al. Accounting for the climate-carbon feedback in emission metrics. Earth Syst. Dynam. 8, 235–253 (2017).
Berntsen, T. K. et al. Response of climate to regional emissions of ozone precursors: sensitivities and warming potentials. Tellus B 57, 283–304 (2005).
Ricke, K. L. & Caldeira, K. Maximum warming occurs about one decade after a carbon dioxide emission. Environ. Res. Lett. 9, 124002 (2014).
Gregory, J. M. & Forster, P. M. Transient climate response estimated from radiative forcing and observedclimate change. J. Geophys. Res. 113, D23105 (2008).
Collins, M. et al. Long-termclimate change: projections, commitment and irreversibility. in Climate Change 2013: The Physical Science Basis (eds Stocker, T. F. & Qin, D. et al.) Ch. 8 (Cambridge University Press, Cambridge, 2013).
Gregory, J. M., Andrews, T. & Good, P. The inconstancy of the transient climate response parameter under increasing CO2. Philos. Trans. R. Soc. A 373, 20140417 (2015).
Millar, R., Allen, M. R., Rogelj, J. & Friedlingstein, P. The cumulative carbon budget and its implications. Oxf. Rev. Econ. Policy 32, 323–342 (2016).
Tokarska, K. B., Gillett, N. P., Weaver, A. J., Arora, V. K. & Eby, M. The climate response to 5 trillion tonnes of carbon. Nat. Clim. Change 5, 851–855 (2016).
Shindell, D. Inhomogeneous forcing and transient climate sensitivity. Nat. Clim. Change 4, 274–277 (2014).
Jenkins, S., Millar, R. J., Leach, N., Allen, M. R. (2018): Framing climate goals in terms of cumulative CO2-forcing-equivalent emissions, Geophys. Res. Lett. https://doi.org/10.1002/2017GL076173 (2018).
Acknowledgements
We are grateful to Ragnhild Skeie for making emissions data available to us from the EDGAR and MATCH databases. M.R.A. & R.J.M. were supported by the Oxford Martin Net Zero Carbon Investment Initiative. D.J.F. and A.H.M. were supported by Victoria University grant 200232. J.S.F. received support from the Research Council of Norway, project no. 235548. R.J.M. was also supported by the Natural Environment Research Council project NE/P014844/1. M.C. was supported by the Oxford Martin Program on Climate Pollutants.
Author information
Authors and Affiliations
Contributions
M.R.A. conceived and led the study. M.C. and R.J.M. performed the calculations behind Fig. 1; all authors contributed to extensive discussions, analysis, interpretation and writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Allen, M.R., Shine, K.P., Fuglestvedt, J.S. et al. A solution to the misrepresentations of CO2-equivalent emissions of short-lived climate pollutants under ambitious mitigation. npj Clim Atmos Sci 1, 16 (2018). https://doi.org/10.1038/s41612-018-0026-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-018-0026-8
- Springer Nature Limited
This article is cited by
-
Alternative climate metrics to the Global Warming Potential are more suitable for assessing aviation non-CO2 effects
Communications Earth & Environment (2024)
-
Defining national net zero goals is critical for food and land use policy
Communications Earth & Environment (2024)
-
Dynamic analysis of geomaterials using microwave sensing
Scientific Reports (2024)
-
The animal agriculture industry, US universities, and the obstruction of climate understanding and policy
Climatic Change (2024)
-
GREENER principles for environmentally sustainable computational science
Nature Computational Science (2023)