Introduction

The Joule–Thomson expansion occurs when a compressed gas is allowed to expand through a porous plug or valve, which reduces the pressure of the gas. As the gas expands, cools down due to reduction of pressure and subsequently its internal energy decreases. The amount of cooling or heating that occurs during the expansion depends on the gas’s specific heat, pressure, and temperature, as well as the nature of the expansion process. Joule–Thomson coefficient, also known as the Joule–Kelvin coefficient, is a measure of the temperature change that occurs during a Joule–Thomson expansion. It is defined as the rate of change of temperature with respect to pressure at a constant Enthalpy. If the Joule–Thomson coefficient for a system is positive, the gas will cool down during the expansion, while if it is negative, the gas will heat up1,2.

Joule–Thomson expansion also has some applications in astrophysics, particularly in the study of black holes thermodynamics. Black holes are massive objects in space that are formed, for instance, from the gravitational collapse of a sufficiently massive star. They are characterized by their event horizon, which is the boundary beyond which nothing, including light, can escape classically.

One of the most interesting properties of black holes is their thermodynamics. In the 1970s Stephen Hawking showed that black holes emit radiation quantum mechanically, known as Hawking radiation, which causes them to lose mass and eventually evaporate. This led to the formulation of black hole thermodynamics, which relates the properties of a black hole, such as its mass, temperature, and entropy, to those of a thermodynamic system3.

Joule–Thomson expansion can be used to model thermodynamics of black holes. In particular, it can be used to calculate the temperature of a black hole which is related to its Hawking radiation. Joule–Thomson coefficient in this case is related to the specific heat of the black hole, which is a measure of its ability to store energy. Joule–Thomson expansion in black holes is also related to the concept of gravitational entropy. Gravitational entropy is a measure of the disorder or randomness of the spacetime around a black hole, and it is related to the amount of information that can be stored in a black hole4,5,6,7. Therefore, Joule–Thomson expansion can be used to calculate gravitational entropy of a black hole, which is related to the amount of information that can be stored in its event horizon.

Here our aim is to extend the concept of Joule–Thomson expansion to the realm of black holes in the context of mimetic gravity. Mimetic gravity is a modified theory of gravity that was proposed in 2013 and avoids the need for a cosmological constant or dark energy to explain late time cosmic speed up. It also provides a natural alternative to the dark matter in the favor of observed rotation curves of spiral galaxies8. Mimetic Gravity is a relatively new approach to gravity that has gained significant attention in the field of theoretical physics, see9,10 and references therein. This theory proposes a different way of understanding gravity by introducing a new set of variables that describe the geometry of spacetime by employing an auxiliary field that mimics the metric tensor. This field is chosen in a way that ensures that the equations of motion for gravity are equivalent to those of General Relativity. Mimetic Gravity was firstly proposed by Chamseddine and Mukhanov in 201311. Since then, it has been further developed by other researchers12,13,14,15, and has shown promising results in addressing some of the fundamental issues in modern cosmology, such as a possibly new route toward better understanding of the nature of dark matter and dark energy; just for some instances see16,17,18.

The key feature of mimetic gravity is that it avoids the need for a cosmological constant or dark energy, which are typically used in general relativity to explain the observed positive acceleration of the expansion of the late time universe. This is a major advantage of the theory, as it provides a more elegant and natural explanation for the positively accelerated expansion of the universe observed in recent years. In fact, the mimetic scalar field acts as a source of the gravitational field, and its dynamics give rise to a positively accelerated expansion. This makes mimetic gravity an attractive alternative to standard cosmology, as it offers a new explanation for the observed cosmic speed up without the need for dark energy or modifications to General Relativity.

Since its proposal, mimetic gravity has generated significant interest in the physics community, and a number of studies have explored its various implications and applications19,20,21,22, see also9,10 and references therein. These include investigations into the theory’s compatibility with cosmological observations, its role in inflationary models, and its potential implications for black hole physics23,24,25,26,27,28. Overal, mimetic gravity represents a promising avenue for exploring the nature of gravity and the universe at large. The action of mimetic gravity can be written in the following form29:

$$\begin{aligned} S=\frac{1}{2\kappa ^{2}}\int d^{4}x\sqrt{-g} [R+\lambda (\phi )(g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi \pm 1)-V(\phi )]+S_{matter}(g_{\mu \nu },\psi ), \end{aligned}$$
(1)

where \(S_{matter}\) is the action for matter fields, \(\kappa ^{2}=8\pi G\), R is the Ricci scalar, \(\phi \) is the mimetic scalar field, \(\lambda (\phi )\) is a function that determines the coupling between the mimetic scalar field and the metric. It is a lagrange multiplier in essence15.

The second term in the action represents the mimetic constraint, which requires that the determinant of the metric to be proportional to the determinant of the mimetic metric, i.e., \(g=-\lambda (\phi )\partial _{\mu }\phi \partial ^{\mu }\phi \). This constraint leads to the appearance of a non-dynamical auxiliary metric that is used to define the physical metric. The action is invariant under general coordinate transformations as well as under the following transformation of the mimetic scalar field: \(\phi \rightarrow \tilde{\phi }(\phi )\), where \(\tilde{\phi }\) is an arbitrary function of \(\phi \). This transformation leaves the mimetic constraint invariant and leads to the same equations of motion for the physical metric.

The equations of motion for mimetic gravity can be derived by varying the action with respect to the metric and the mimetic scalar field. The resulting equations are highly non-linear and are difficult to solve in general. However, in certain cases, mimetic gravity can lead to interesting cosmological solutions that are free from instabilities and avoid the need for dark energy or a cosmological constant8,9,10. Varying the action with respect to \(g_{\mu \nu }\) gives the Einstein field equations as

$$\begin{aligned} G_{\mu \nu }=\kappa ^{2}T^{(eff)}_{\mu \nu }, \end{aligned}$$
(2)

where \(G_{\mu \nu }\) is the Einstein tensor, \(T_{\mu \nu }^{(eff)}\) is the effective stress-energy tensor that includes both the matter stress-energy tensor \(T_{\mu \nu }^{(m)}\) and the contribution from the mimetic scalar field:

$$\begin{aligned} T^{(eff)}_{\mu \nu }=T_{\mu \nu }^{(m)}+\Theta _{\mu \nu }, \end{aligned}$$
(3)

where \(\Theta _{\mu \nu }\) is the contribution from the mimetic scalar field as follows:

$$\begin{aligned} \Theta _{\mu \nu }=\lambda [2\partial _{\mu }\phi \partial _{\nu }\phi -g_{\mu \nu }(\partial ^{\alpha } \phi \partial _{\alpha }\phi +1)]-V(\phi )g_{\mu \nu }. \end{aligned}$$
(4)

Varying the action with respect to \(\phi \) gives the mimetic scalar field equation as

$$\begin{aligned} \partial ^{\nu }(\lambda \partial _{\mu }\phi )-V'(\phi )=0 \end{aligned}$$
(5)

where \(V'(\phi ) = dV/d\phi \). Together, these equations describe the dynamics of gravitational and mimetic scalar fields in the context of mimetic gravity.

After an introduction to the main idea and related literature, in what follows we investigate some novel thermodynamic aspects of a mimetic black hole by focusing on the issue of Joule–Thomson expansion and related problems.

We note that the issue of Joule–Thomson expansion has been studied in various contexts, our work extends these studies to the framework of mimetic gravity for the first time. This extension is not just a mathematical exercise; it provides insights into how new gravitational theories, such as the mimetic gravity, can influence thermodynamic processes in gravitational systems such as a black hole. On the other hand, deeper insight into the phenomenon such as the Joule–Thomson expansion in the context of the Mimetic Gravity, sheds more light on the way to understand the structure of this new gravitational theory. Since Mimetic Gravity introduces a scalar field that mimics dark matter (and also dark energy) and modifies the gravitational field equations, this modification can lead to different thermodynamic behaviors in this setup.

Thermodynamic aspects and Joule–Thomson expansion in mimetic black hole

Mimetic black hole solution

The static spherically symmetric solution of mimetic gravity can be obtained by considering the following metric ansatz29:

$$\begin{aligned} ds^{2}=-A(r)dt^{2}+\frac{1}{B(r)}dr^{2}+C(r)d\Omega ^{2}, \end{aligned}$$
(6)

where \(d\Omega ^2\) is the metric on the unit 2-sphere and \(A(r)>0\) and \(B(r)>0\) are functions that depend on the mimetic scalar field \(\phi \) and the radial coordinates for the exterior soloution29,

$$\begin{aligned} A(r)=\frac{1}{4r^{4}\lambda ^{2}},\quad B(r)=1-\frac{2m}{r},\quad C(r)=r^{2} \end{aligned}$$
(7)

The action (1) for mimetic gravity in the absence of potential and ordinary matter sources is given by:

$$\begin{aligned} S=\frac{1}{2\kappa ^{2}}\int d^{4}x\sqrt{-g} [R+\lambda (\phi )(g^{\mu \nu }\partial _{\mu }\phi \partial _{\nu }\phi \pm 1)] \end{aligned}$$
(8)

The equations of motion for this action can be obtained by varying the action with respect to the metric tensor \(g_{\mu \nu }\) and the scalar field \(\phi \), the results of which are as follows

$$\begin{aligned} & R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=-2\kappa \lambda \partial _{\mu }\phi \partial _{\nu }\phi \end{aligned}$$
(9)
$$\begin{aligned} & \lambda =\frac{1}{2r^{2}}\left[ 1-\sqrt{1-\frac{2m}{r}}\left( \frac{1}{\sqrt{1-\frac{2m}{r_{f}}}} +\ln {\sqrt{\frac{r}{r_{f}}}}\frac{1+\sqrt{1-\frac{2m}{r}}}{1+\sqrt{1-\frac{2m}{r_{f}}}}\right) \right] ^{-1} \end{aligned}$$
(10)
$$\begin{aligned} & \phi =r\sqrt{1-\frac{2m}{r}}+2m\ln {\left( \sqrt{\frac{r}{c_{3}}}\left( 1+\sqrt{1-\frac{2m}{r}}\right) \right) } \end{aligned}$$
(11)

where \(c_{3}\) is a constant of integration that has no significant impact in forthcoming arguments since the setup is shift-symmetric. As for \(r_{f}\), it represents the radial position of the caustic singularity. In mimetic gravity, caustic singularities are points in space-time where the mimetic field’s gradient becomes zero. These singularities can occur in the interior of mimetic black holes and are characterized by the formation of a caustic surface29. At this surface, the null geodesics become focused, leading to the appearance of an infinitely high concentration of energy density. The caustic singularity is not a curvature singularity, but rather a feature of the mimetic field. It arises due to the non-invertibility of the mimetic mapping from the physical space-time to the mimetic space-time, which leads to the formation of regions where the mimetic field is not a smooth, well-defined function.

By using Eqs. (9)–(11), one can calculate the components of the stress-energy tensor and obtain the pressure P. The resulting expression for the pressure in a mimetic black hole is quite complicated and depends on the specific form of the mimetic scalar field. The energy-momentum tensor for the mimetic scalar field is given by Eq. (9) as (with \(\kappa =1\))

$$\begin{aligned} T_{\mu \nu }=-2\lambda \partial _{\mu }\phi \partial _{\nu }\phi . \end{aligned}$$
(12)

In the context of Joule–Thomson expansion in black holes, one may want to investigate the change in temperature and entropy of the black hole as a result of the expansion/compression process. In particular, one may want to calculate the Joule–Thomson coefficient, which relates the change in temperature to the change in pressure during the expansion/compression process. This coefficient can be expressed in terms of the specific heat at constant pressure and the speed of sound in the fluid, which in the case of black holes are related to the thermodynamic properties of the event horizon.

Temperature and entropy

By using the tunneling formalism, where a particle can tunnel through the event horizon of a black hole, it was shown that the temperature of any black hole in asymptotically flat or (A)dS space can be expressed as follows30

$$\begin{aligned} T=\frac{1}{4\pi }\sqrt{A_{,r}(r)B_{,r}(r)} \end{aligned}$$
(13)

where \(A_{,r}\) means \(\frac{dA}{dr}\) and also \(B_{,r}=\frac{dB}{dr}\). Following this relation, in our mimetic setup we find

$$\begin{aligned} T=\frac{\left( -\frac{m r_{f} \left( 2m \left( 1 + \sqrt{1 - \frac{2m}{r}} - \sqrt{1 - \frac{2m}{r_{f}}}\right) + \left( 1 + \sqrt{1 - \frac{2m}{r}}\right) r \sqrt{1 - \frac{2m}{r_{f}}} + 2m \left( 1 + \sqrt{1 - \frac{2m}{r}}\right) \sqrt{1 - \frac{2m}{r_{f}}} \ln {\left( \frac{\left( 1 + \sqrt{1-\frac{2m}{r}}\right) \sqrt{\frac{r}{r_{f}}}}{1 + \sqrt{1 - \frac{2m}{r_{f}}}}\right) }\right) }{r^{3} \left( -2m + r + \sqrt{1 - \frac{2m}{r}} r\right) \left( 2m-r_{f}\right) }\right) ^{\frac{1}{2}}}{2\sqrt{2}\pi } \end{aligned}$$
(14)
Figure 1
figure 1

The plot of T given in Eq. (14) versus the radial coordinate r for m=1 and \(r_{f} = 4\). There is a singularity at \(r = r_{f}\) after which the curvature changes sign. The Schwarzschild black hole temperature \(T=\frac{1}{4 \pi r}\) is shown with blue color. In mimetic gravity black hole temperature raises to a maximum value due to evaporation and then decreases. There is a black hole remnant in this mimetic framework as is evident in this figure, see also25.

Full size image

Figure 1 shows the behavior of temperature versus the radial coordinate. It is seen that in the mimetic balck hole case, the temperature of black hole increases by evaporation until it reaches to a maximum at \(r_{f}\) and then tends to zero with a black hole remnant. This is much similar to quantum-corrected and also non-commutative black hole cases31. Entropy, as another important thermodynamic quantity is given as

$$\begin{aligned} S=\frac{A}{4}, \qquad A=\int _{0}^{\pi }\int _{0}^{2\pi }\sqrt{g_{\theta \theta }g_{\phi \phi }}d\theta d\phi , \end{aligned}$$
(15)

Now, the action (8) is similar to the Einstein–Hilbert action, but with an additional term that includes the mimetic field \(\phi \). In this case, the mimetic field still contributes to the spacetime curvature, even in the absence of any other matter fields. This is because the mimetic field induces an energy density that is proportional to \(\lambda \) and depends on the spacetime geometry. Aditionally, the curvature invariants do not vanish, \(R=2\lambda \), meaning that the spacetime still has curvature effects29.

Pressure

In a standard scenario without a mimetic field, where the cosmological constant takes on the role of a thermodynamic variable, the pressure is characterized as follows

$$\begin{aligned} P=-\frac{1}{8\pi }\Lambda =\frac{3}{8\pi }\frac{1}{l^{2}} \end{aligned}$$
(16)

where the symbols l and \(\Lambda \) represent the Anti-de Sitter (AdS) radius and cosmological constant, respectively. When the mimetic scalar field becomes a non-zero contributor to the background, with \(\lambda \ne 0\), the resulting solution deviates from the stealth configuration and differs from a Schwarzschild black hole. In this context, it serves as an analog to mimetic dark matter (energy), where the mimetic field assumes the role of dark matter (energy) within a cosmological background characterized by \(\lambda \ne 0\). In this scenario, the mimetic field acts as a thermodynamic variable that introduces pressure into the system. Since \(T_{\mu \nu }=-2\lambda \partial _{\mu }\phi \partial _{\nu }\phi \), the pressure is defined in radial component as

$$\begin{aligned} P= \frac{\sqrt{1 - \frac{2m}{r_{f}}}}{r(-2m + r)\left( \sqrt{1 - \frac{2m}{r}} - \sqrt{1 - \frac{2m}{r_{f}}} + \sqrt{1 - \frac{2m}{r}}\sqrt{1 - \frac{2m}{r_{f}}}\ln \left( \frac{(1 + \sqrt{1 - \frac{2m}{r}})\sqrt{\frac{r}{r_{f}}}}{1 + \sqrt{1 - \frac{2m}{r_{f}}}}\right) \right) }, \end{aligned}$$
(17)

and is not the same in the radial and angular directions. This is a complicated relation and it is hard to see the behavior of pressure in radial distances analytically. However, Figure 2 illustrates the radial variation of the pressure in this mimetic setup. As was expected, there is a discontinuity in pressure at \(r=r_{f}\). The interesting feature is that pressure in radial distances smaller than \(r_{f}\) is negative which can be a reminiscent of the dark energy behavior.

Figure 2
figure 2

The plot of pressure given in Eq. (17) versus the radial coordinate r for \(m = 1\) and \(r_{f}=4\). There is a singularity at \(r=r_{f}\) after which the pressure changes sign and gets negative.

Full size image

This thermodynamic parameter exhibits a gradual shift from a positive value within the \(0<r_{f}< r\) region and eventually tends toward zero as \(r\rightarrow \infty \) as shown in Fig. 2.

To see these features more closely, we set \(m=0\) in the discontinuities of Eq. (6) and then by using the relation (7) with spatially flat surface, (6) takes the following form

$$\begin{aligned} ds^{2}=-(\ln r/r_{f})^2 dt^2+dr^2+r^2d\Omega ^2. \end{aligned}$$
(18)

The logarithmic factor inside the parentheses shows that time is measured differently depending on the radial position r. As r approaches \(r_{f}\), the logarithm diverges to negative infinity, indicating that time slows down indefinitely. The caustic horizon, located at \(r=r_{f}\), is another important feature of the metric, the logarithm there is zero, indicating that time stops. This feature is particularly relevant for the study of black holes, where time is expected to behave differently near the event horizon. As mentioned earlier, this is the surface beyond which light rays that approach the black hole from infinity are focused into a ring of light before entering the event horizon. The curvature invariant does not vanish in the case \(m=0\)

$$\begin{aligned} R= -\frac{1}{r^2 \ln \left( \sqrt{\frac{r}{r_f}}\right) }. \end{aligned}$$
(19)

Figure 3 shows the behavior of the curvature invariant, R, versus the radial coordinate. When \(r< r_{f}\), the curvature invariant is finite and positive. At \(r\gg r_{f}\), the curvature invariant becomes negative and smaller as r increases. This means that the spacetime is less curved at larger distances from the caustic singularity. As r becomes much larger than \( r_{f}\), the curvature invariant approaches zero, which corresponds to a flat spacetime.

Figure 3
figure 3

The plot of R versus the radial coordinate r for \(m = 0\) and \(r_{f}=4\).

Full size image

In de Sitter (dS) spacetime, the pressure is a negative constant which is equal in magnitude to the cosmological constant. This is because the dS spacetime is characterized by a positive cosmological constant, which acts as a type of vacuum energy and exerts a negative pressure (anti-gravitation, repulsion) throughout the spacetime. Negative pressure is responsible for driving the positively accelerated expansion of the universe that is observed in current observational data.

In contrast, in an Anti-de Sitter (AdS) spacetime, the pressure is a positive constant, which is also equal in magnitude to the cosmological constant. This is because AdS spacetime is characterized by a negative cosmological constant, which leads to a type of vacuum energy that exerts a positive pressure (attraction) throughout the spacetime. AdS spacetime is often studied in the context of AdS/CFT correspondence, which is a conjectured relationship between gravitational theories in AdS spacetime and conformal field theories (CFTs) living on the boundary of AdS spacetime. In our case we have

$$\begin{aligned} P=-2\lambda \partial _{r}\phi \partial _{r}\phi =\frac{1}{r^{2}\ln [\sqrt{\frac{r}{r_{f}}}]} \end{aligned}$$
(20)

which shows that pressure for \(r>r_{f}\) is positive and for \(r<r_{f}\) it is negative. Therefore, it can be concluded that \(r>r_{f}\) region corresponds to the anti de Sitter and the \(r<r_{f}\), corresponds to the de Sitter space.

Now, let’s consider the simplest type of geodesics, which is, the radial null geodesics. A “radial” null geodesic means \(ds^{2}=0\) while \(\theta \) and \(\phi \) are constants along the geodesic, so the metric on the geodesic is

$$\begin{aligned} dt=\pm \frac{dr}{\sqrt{(\ln [\frac{r}{r_{f}}])^{2}}} \quad \Rightarrow \quad t=r_{f}\frac{\ln [\frac{r}{r_{f}}]Li [\frac{r}{r_{f}}]}{\sqrt{\log \frac{r}{r_{f}}}}+\left( {\begin{array}{c}u\\ v\end{array}}\right) , \end{aligned}$$
(21)

where Li is logarithmic integral function or integral logarithm and u and v will be defined in what follows. t diverges logarithmically as \(r\rightarrow r_{f}\). To solve this problem one can define a new radial coordinate as

$$\begin{aligned} dr^{\star }=\frac{dr}{\sqrt{(\ln [\frac{r}{r_{f}}])^{2}}}. \end{aligned}$$
(22)

Along a radial null geodesic we have

$$\begin{aligned} \frac{dt}{dr^{\star }}=\pm 1 \end{aligned}$$
(23)

Let’s define new coordinates v and u along the ingoing and outgoing radial null geodesics as,

$$\begin{aligned} v=t+r^{\star },\quad \quad u=t-r^{\star }. \end{aligned}$$
(24)

Now we can use \((v,r,\theta ,\phi )\) as coordinates instead of \((t,r,\theta ,\phi )\), so we can introduce ingoing lightlike metric as

$$\begin{aligned} ds^{2}=-\left( \ln \left[ {\frac{r}{r_{f}}}\right] \right) ^{2}dv^{2}+2dvdr +\left( 1-\frac{1}{\left( \ln \left[ {\frac{r}{r_{f}}}\right] \right) ^{2}}\right) dr+r^{2}d\Omega ^{2}. \end{aligned}$$
(25)

If we define

$$\begin{aligned} 1-\frac{2m}{r}=\tan {\alpha }, \end{aligned}$$
(26)

we need to find the value of \(\alpha \) for different values of r, as follows.

For \(r=0\) we find \(\alpha =\frac{\pi }{2}\). For \(r = 2m\), \(\alpha \) can take any value of \(n\pi \), where n is an integer. When r approaches infinity, it means that the equation \(1-\frac{2m}{r}=\tan {\alpha }\) reduces approximately to \(\tan \alpha =1\). The solution to this equation is \(\alpha =\pi /4 + n\pi \), and we have

$$\begin{aligned} \lambda =\frac{(\tan {\alpha }-1)^{2}}{8m^{2}\left[ 1-\left( \frac{1}{\sqrt{1-\frac{1}{\tan ^{-1}{r_{f}}}}} +\ln (\frac{(1+\sqrt{\tan {\alpha } })(\frac{1}{\tan ^{-1}{r_{f}}-\tan ^{-1}{r_{f}}\tan {\alpha }})}{1+\sqrt{1-\frac{1}{\tan ^{-1}{r_{f}}}}})\right) \right] }, \end{aligned}$$
(27)

and

$$\begin{aligned} \phi =2m\left( \ln \left[ \sqrt{2}(1+\sqrt{\tan {\alpha }})\sqrt{\frac{m}{c_{3}(1-\tan {\alpha })}}\right] +\frac{\sqrt{\tan {\alpha }}}{1-\tan {\alpha }}\right) \end{aligned}$$
(28)

By performing the conversion of \(r_{f}\rightarrow r'_{f}=2m\tan ^{-1}{r_{f}}\), which originally spans the entire domain of (0,\(\infty \)) to the \(r_{f}\) domain, the range of values for the variable can be restricted to the interval (0, \(\pi \)/2). This transformation allows for a more compact representation of the space and enables a focused analysis within a specific range of values. This restriction facilitates a detailed investigation of the system’s behavior and properties within the limited region, providing valuable insights into the underlying dynamics.

Joule–Thomson expansion

The accretion disk is a region of hot gas and plasma that surrounds a black hole and is in orbit around it. In this region strong gravitational field can create a significant pressure gradient. This pressure gradient can cause the gas to expand and cool as it moves away from the black hole, which is similar to the process that occurs in a Joule–Thomson expansion. Overall, the Joule–Thomson expansion can occur in the region surrounding a black hole, where the strong gravitational field can create a pressure gradient that causes the gas to expand and cool.

For \(n=0\) we can approximate (26) by assuming that \(\alpha \) is small. This means that \(\tan {\alpha }\approx \alpha \). Therefore, we can rewrite the equation as:

$$\begin{aligned} \alpha \approx 1-\frac{2m}{r} \end{aligned}$$
(29)

Therefore, with the given explanation, the metric can be extended near the event horizon. In the new coordinate approximation form of (27) and (11) we have:

$$\begin{aligned} \lambda =\frac{1 + \frac{\alpha }{-1 + tan^{-1}(r_{f})} + \sqrt{\alpha } \ln \psi + \alpha \ln \psi ^2 + \left( \sqrt{\alpha } + \frac{2\alpha \ln \psi }{\xi }\right) }{2 r^{2}}, \end{aligned}$$
(30)

where by definition

$$\begin{aligned} & \psi =\left( \frac{\sqrt{\frac{1}{tan^{-1}r_{f}}}}{1 + \sqrt{1 - \frac{1}{tan^{-1}r_{f}}}}\right) , \qquad \xi =\sqrt{1 - \frac{1}{tan^{-1}r_{f}}} \end{aligned}$$
(31)
$$\begin{aligned} & \phi =m\ln \left[ \frac{2m}{c_{3}}\right] +4m\sqrt{\alpha }. \end{aligned}$$
(32)

So, by using (27) and (32) the mimetic metric near the horizon can be described as follows

$$\begin{aligned} & ds^{2}=-A(r_{f})dt^{2}+\frac{4m^{2}}{B(r_{f})}d\alpha ^{2}+4m^{2}(1+\alpha )^{2}d\Omega ^{2} \end{aligned}$$
(33)
$$\begin{aligned} & A(r_{f})\approx 1+\left( -\frac{2}{\xi }-2\ln \psi \right) \sqrt{\alpha }+\left( -2+\left( \frac{1}{\xi }+\ln \psi \right) ^{2}\right) \alpha \quad \end{aligned}$$
(34)
$$\begin{aligned} & B(\alpha )\approx \alpha \end{aligned}$$
(35)

The corresponding thermodynamic quantities are then

$$\begin{aligned} & S=\pi r^{2} (1+\alpha )^{2} \end{aligned}$$
(36)
$$\begin{aligned} & T=\frac{\sqrt{-2+\frac{-2+\frac{-2}{\xi }-2\ln \psi }{2\sqrt{\alpha }}+(\frac{1}{\xi }+\ln \psi )^{2} }}{4\pi r} \end{aligned}$$
(37)
Figure 4
figure 4

The plot of T as given in Eq. (37) versus the radial coordinate r for \(\alpha \)=1 and \(r_{f}\)=2. Schwarzschild black hole temperature is shown by the red curve.

Full size image

Figure 4 shows the behavior of temperature versus the radial coordinate as given by Eq. (37).

To be able to compare the temperature in the new coordinates with the Schwarzschild temperature, we came to the conclusion to write the Schwarzschild metric in the new coordinates in terms of \(\alpha \) using Eq. (26), and in this case, the temperature will be \(T=\frac{\sec {\alpha }}{4 \pi r}\). Then we find,

$$\begin{aligned} P=-\frac{1+\frac{\alpha }{-1+\tan ^{-1}{r_{f}}}+\ln \psi \sqrt{\alpha }+\ln \psi ^{2}\alpha +\frac{\sqrt{\alpha }+2\alpha \ln \psi }{\xi }}{\alpha r^{2} }. \end{aligned}$$
(38)

By substituting the expression from (38) into (37), the Hawking temperature of the mimetic black hole can be expressed as a function of pressure

$$\begin{aligned} T=\frac{\sqrt{-2-Pr^{2}+\frac{1}{\xi ^{2}}+\frac{-1+r^{2}\sqrt{\frac{-4Pr^{2}-\frac{3}{\alpha } +\frac{4}{\xi ^{2}}-\frac{4}{-1+tan^{-1}r_{f}}}{r^{4}}}}{\sqrt{\alpha }}+\frac{1}{1-tan^{-1}r_{f}}}}{4\pi r} \end{aligned}$$
(39)

In this case, the heat capacity takes the following form

$$\begin{aligned} C_{p}=T\frac{\partial S}{\partial T}= \frac{128 \pi ^3 r^4 T^2 \alpha ^{3/2} (1 + \alpha ) \xi }{(1 + \xi ) \ln \psi } \end{aligned}$$
(40)

Figure 5 plots the behavior of heat capacity in constant pressure versus the radial distance for \(r_{f}=2\).

Figure 5
figure 5

Plot of C p versus r with the conditions: \(\alpha =0.02\) and \(r_{f}=2\) green line, \(\alpha =1\) and \(r_{f}=2\) blue line and schwartschild BH heat capacity the red line.

Full size image

Mathematically, the Joule–Thomson coefficient is defined as

$$\begin{aligned} \mu&= \frac{\partial P}{\partial T}_{_{H}}= \frac{1}{C_{p}}\left[ T\left( \frac{\partial {V}}{\partial {T}}\right) _{P}-V\right] \\&\frac{8\left(-3+r^{2}\sqrt{\alpha }\sqrt{{\frac{-4Pr^{2}-\frac{3}{\alpha }+\frac{4}{\xi ^{2}} -\frac{4}{-1+\tan ^{-1}r_{f}}}{r^{4}}}}\right)\sqrt{-2-Pr^{2}+\frac{1}{\xi ^{2}} +\frac{-1+r^{2}\sqrt{\frac{-4Pr^{2}-\frac{3}{\alpha }+\frac{4}{\xi ^{2}} -\frac{4}{-1+\tan ^{-1}r_{f}}}{r^{4}}}}{\sqrt{\alpha }}+\frac{1}{1-\tan ^{-1}r_{f}}}}{r+r^{3}\sqrt{\alpha }\sqrt{\frac{-4Pr^{2}-\frac{3}{\alpha }+\frac{4}{\xi ^{2}}-\frac{4}{-1+\tan ^{-1}r_{f}}}{r^{4}}}} \end{aligned}$$
(41)

In this case, the heat capacity takes the following form

$$\begin{aligned} C_{p}=T\frac{\partial S}{\partial T}= \frac{128 \pi ^3 r^4 T^2 \alpha ^{3/2} (1 + \alpha ) \xi }{(1 + \xi ) \ln \psi } \end{aligned}$$
(42)

Figure 6 illustrates the behavior of the Joule–Thomson coefficient versus the radial coordinate. The influence of various values of \(r_{f}\) is depicted and revealing a consistent pattern across different scenarios, indicating a definite behavior.

Figure 6
figure 6

Plot of \(\mu \) (the Joule–Thomson coefficient) versus r for different values of \(r_{f}\).

Full size image

The Joule–Thomson coefficient can be positive or negative, depending on the type of the gas and the physical conditions. If \(\mu >0\), the gas cools down when it expands (lowering the pressure) at constant enthalpy or internal energy. This is often the case for gases that behave like an ideal gas under the given conditions. If \(\mu <0\), the gas heats up when it expands at constant enthalpy or internal energy. This behavior is typically observed for real gases under certain conditions, especially when the gas is close to condensing into a liquid.

From Eq. (41) the inversion temperature can be obtained by taking \(\mu = 0\) as follows (see also Ref.32)

$$\begin{aligned} T_{i}=V\left( \frac{\partial {T}}{\partial V}\right) _{P}=\frac{4 - \frac{2}{{\xi ^{2} }} - \frac{{2\left( { - 1 + r^{2} \sqrt {\frac{{ - 4Pr^{2} - \frac{3}{\alpha } + \frac{4}{{\xi ^{2} - \frac{1}{{ - 1 + tan^{{ - 1}} r_{f} }}}}}}{{r^{4} }}} } \right)}}{{\sqrt \alpha }} - \frac{{4P}}{{\sqrt \alpha \left. {\sqrt {\frac{{ - 4Pr^{2} - \frac{3}{\alpha } + \frac{4}{{\xi ^{2} - \frac{1}{{ - 1 + tan^{{ - 1}} r_{f} }}}}}}{{r^{4} }}} } \right)}} + \frac{2}{{ - 1 + tan^{{ - 1}} r_{f} }}} {24\pi r \sqrt{-2-Pr^{2}+\frac{1}{\xi ^{2}}+\frac{-1+r^{2}\sqrt{\frac{-4Pr^{2}-\frac{3}{\alpha }+\frac{4}{\xi ^{2}} -\frac{4}{-1+tan^{-1}r_{f}}}{r^{4}}}}{\sqrt{\alpha }}+\frac{1}{1-tan^{-1}r_{f}}}} \end{aligned}$$
(43)
Figure 7
figure 7

Inversion temperature versus the radial distance for three different conditions.

Full size image

Figure 7 shows the behavior of \(T_{i}\) versus the radial coordinate. When \(r_{f}=2.3\), the temperature of the black hole is approximated as \(T\approx \frac{1}{4\pi r}\) for distances near the event horizon, where \(\frac{r}{m}\approx 1\), and this approximation holds true under the assumption that \(0<\alpha \le 1\). Bysome simplifications, other thermodynamic quantities in this approximation are obtained as follows

$$\begin{aligned} P\approx -\frac{7.6}{r^{2}};\qquad C_{P}\approx 3456\, r^{4}T^{2}, \quad \mu \approx 590 T \end{aligned}$$
(44)

Subtracting equation (43) from equation (39) one can find positive root of r and put it into (43) at \(P = P_{i}\), where the inversion temperature is re-derived.

Figure 8
figure 8

Plots of inversion curves \(P_{i}\) versus \(T_{i}\).

Full size image

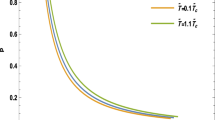
If we set \(P_{i}=0\), the minimum inversion temperature is \(T^{min}_{i}=0\), indicating that the black hole transits into an extremal black hole. Finally, Fig. 8 shows the inversion curves for a mimetic black hole with different values of the parameters \(\alpha \) and \(r_{f}\). As we see these inversion cures follow more or less the same scheme as other black hole solutions as expected. We note that negative pressure can be considered as a quantum effect in free streaming in a cosmological background as has been discussed in Ref.33. So, the negative pressure we encountered in this setup can be justified at least in this background.

Discussion

In what follows, we stress on two important issues: firstly, our analysis reveals how the mimetic field affects the inversion temperature and the cooling-heating regions in the Joule–Thomson expansion. These results could have implications for understanding the thermodynamics of black holes in modified gravity theories, potentially impacting our comprehension of black hole physics and cosmology. In addition, our analysis reveals the presence of two distinct regions \(r<r_{f}\) and \(r>r_{f}\). While the region outside the black hole \(r>r_{f}\) is Ads space, the Joule–Thomson expansion is applicable only in this outer region. However, for this calculation, we must exclude the dS space \(r<r_{f}\) because it lies within the event horizon of the black hole, a region where our current understanding of physics is limited. Recently some progress in this field has been reported; see Refs.34,35,36.

Secondly, the negative pressure in our framework is indeed associated with the de Sitter (dS) case. There are some concerns regarding the interpretation of black hole temperature and equilibrium state in this case. In what follows we try to elaborate on the thermodynamic properties of black holes in the dS space, specifically addressing how negative pressure influences the temperature and equilibrium states. This includes a more detailed discussion on the stability and physical implications of our results. We note that in the context of black holes within a mimetic background, the Joule–Thomson expansion can be investigated in the region outside the event horizon. This region, also known as the AdS (Anti de Sitter) space, exhibits positive pressure, as shown in Fig. 2.

However, the pressure diverges at a specific radius, \(r=r_{f}\) where two horizons would hypothetically overlap. This scenario is physically unrealistic. Moving further away from the black hole, the spacetime becomes increasingly flat, and the pressure approaches zero (in the absence of a cosmological constant). In the presence of the cosmological constant the pressure would be \(P=-\frac{\Lambda }{8\pi }\) . Therefore, for the region outside the event horizon, a positive pressure description is valid. It is important to emphasize, however, that the concept of pressure itself becomes questionable near the event horizon due to the extreme gravitational influence. Here, the traditional notions of fluids and pressure might not hold entirely true. Recent researches exploring models for the interior of collapsed objects suggest the presence of negative pressure within the horizon. Also recently it has been demonstrated that negative temperature regions within black holes naturally lead to negative pressure. This phenomenon provides an outward force counteracting the gravitational collapse, thereby stabilizing the black hole. This suggests that negative pressure plays a crucial role in the thermodynamic properties and stability of black holes, offering new insights into their complex nature, see for instance Refs.34,35,36.

We note that for the de Sitter case, we are actually dealing with a Schwarzschild- de Sitter like state with two horizons. The temperature of these horizons can be calculated as the period in imaginary time of the solution or equivalently the surface gravities near the horizons. Nevertheless, the temperature of the dS black hole is hard to be defined since there is no asymptotically flat space to measure it relative to. We refer to Ref.37, Eq (12) for an attempt in this respect, see also Ref.38. Our study in this work shed lights on the issue from a mimetic gravity point of view. We hope to delve into this fundamental issue in our forthcoming works.

Summary and conclusion

Mimetic gravity has the capability to provide a natural explanation of the dark sectors, that is, dark matter and dark energy. Black hole solutions in alternative theories of gravity reflect the essence of these theories in strong gravity regime and for this reason studies of black hole solutions and their characteristics in mimetic gravity has its own importance. While mimetic black hole has been studied vastly in recent years, there is an obvious gap in this field regarding the thermodynamic aspects of mimetic black holes via the Joule–Thomson expansion. The present study has been devoted to this issue and fills the mentioned gap. We firstly have summarized the action description of the mimetic gravity along with field equations and some of their specific features. Then, the main thermodynamic quantities for a mimetic black hole have derived in details along with their physical interpretation via numerical analysis and appropriate illustrations. Then the Joule–Thomson expansion and related issues are studied in details towards a thorough understanding of mimetic black hole evaporation in this setup. Our investigation has illuminated the pressure distribution, unveiling a considerable discontinuity at the event horizon (\(r=r_f\)). Remarkably, negative pressure in radial distances smaller than \(r_f\) echoes the dark energy behavior, providing a unique view through which to understand the thermodynamics of mimetic black holes. Furthermore, introduction of new coordinates allowed us to express the mimetic metric near the horizon, showcasing a temperature profile that differentiates from the Schwarzschild black hole. The temperature profile of the mimetic black hole shows that by evaporation of the black hole, its temperature grows up to a maximum value and then drops to the temperature of a black hole remnant. The heat capacity for this mimetic black hole which reflects the possibility of phase transitions exhibited intriguing behavior under constant pressure conditions. We then explored into the Joule–Thomson coefficient, unveiling its dependence on the mimetic field and temperature. The inversion temperature and inversion curves in this setup are treated extensively and their characteristics are explored both mathematically and numerically. In conclusion, our study significantly advances understanding of the mimetic gravity’s influence on black hole thermodynamics. By bridging the realms of gravitational physics and thermodynamics, this work opens avenues for future exploration, promising a deeper comprehension of the fundamental nature of gravity within the framework of mimetic theories.