Introduction

NiV is a zoonotic vial infection that belongs to the Paramyxoviridae family. It can be transmitted through contaminated food and directly between humans1. The virus can cause various respiratory infections in both animals and humans1. The Pteropus genus, specifically the Pteropodidae family of flying foxes are the natural reservoir for the NiV1,2. More than 50 different species of Pteropus bats are fount in the south and southeast Asian regions3. NiV can be transmitted to humans through various transmission routes, either directly from flying foxes or indirectly from animals that have been infected by them. Another mean of viral transmission is through unsafe contact with the dead body of an infected person prior to their funeral or burial1,2,3,5. A person infected with Nipah experience symptoms like headache, fever, and tiredness during the first 2 weeks after virus exposure. These symptoms in some cases lead to a coma within 2 days6,7. There is currently no vaccine available to prevent the NiV, so the best way to contain its spread is by educating people and raising awareness3.

NiV was first discovered during an outbreak of encephalitis and respiratory diseases in a Malaysian village called Sungai Nipah. From September 1998 till April 1999, there were 265 infected cases resulting in 105 mortalities. It was found that pigs were the carriers of the virus, and they infected pig farmers, leading to the outbreak5,8. In 1998, Malaysia experienced a severe Nipah epidemic, and from 2001 to 2012, occasional outbreaks of the disease occurred in Bangladesh. Nipah also re-emerged periodically in India near the Bangladesh border and West Bengal. Furthermore, in 2018, a Nipah outbreak occurred in Kerala, a southern region of India, even though it was 2,800 kilometers away from the Bangladesh border and was not in the usual outbreak season.

In South-East Asian nations, palm sap obtained from date palms is widely consumed3. The crop is typically collected in the colder months, especially in the rural areas of Bangladesh9. Flying foxes contaminate date palm sap with excretions like saliva and urine when feeding. In Bangladesh, it has been observed that Nipah disease can be transmitted to humans through the consumption of contaminated fruits or fruit products that might have been contaminated by flying foxes10. The transmission from human-to-human was identified during the NiV outbreak in Bangladesh reported 200411. The infection was transfer to the individuals who had direct exposure to the body fluids of individuals infected with NiV, or through the use of contaminated materials such as towels, bedsheets, etc. This included medical practitioners, family caregivers, and hospital visitants12.

Mathematical modeling is a useful approach for analyzing and simulating real-life problems, including epidemic outbreaks13,14,15,16. These models are usually constructed via system of ordinary or partial differential equations and are helpful to set an effective control interventions for disease minimization17,18,19. Various compartmental models can be found in the existing literature that explain the transmission dynamics of the NiV incidence in different countries and suggest possible effective measures to eradicate it. In20, a transmission modeling approach was utilized to determine the optimal preventive measures for the control of NiV in the population of Bangladesh. Beside this many papers have been published to explore the dynamical aspects of the infection transmission and possible controlling strategies. Mondal et al.21 examined a compartmental model to explore how prevention strategies can minimize the incidence of disease. Shah et al.22 proposed a SEI-type mathematical model considering multiple transmission modes, including among humans transmission through contact with deceased NiV patients. Nita et al.23 proposed a new epidemic model that takes into account the connection between bats and humans, incorporating various control strategies such as hospitalizations, self-prevention, spraying pesticides, and burying flying foxes. Agarwal and Singh24 proposed a transmission model that accounts for both human and flying fox populations, which has significant implications for understanding and preventing the transmission of zoonotic diseases. A recent analysis focusing on the mitigation of NiV via a Caputo fractional optimal control problem was presented in25. The global dynamics and various transmission aspects of NiV were studied in26,27,28.

This research emphasizes on presenting a comparative analysis of time-dependent and constant controlling strategies for the mitigation of NiV with vaccination and treatment using optimal control theory. To do so, we develop a compartmental model that considers various factors, building on previous research. A sensitivity analysis will be performed to find out the influential parameters embedded in the model. Optimal control theory will then be applied by introducing six control variables to mitigate the incidence of the infection in the community. The paper is divided into seven sections. In the next section the development procedure of the model with brief description of the parameters will be presented. Section “Qualitative analysis of NiV model” covers qualitative analysis, calculation of reproduction number, and performing stabilities. Section “Application to the outbreak reported in Bangladesh during 2001–2015” discusses data fitting. In the section “Sensitivity of the threshold parameters” a normalized sensitivity analysis of the model parameters is conducted. Section “Formulation of the optimal control NiV model” focuses on optimal control analysis, numerical simulations, and graphical results. The final concluding remarks are shown in section “Conclusion”.

Model formulation with constant control measures

This section presents a brief procedure used to develop the proposed model exploring the dynamics of NiV. The transmission of the virus can occur via two modes: food-borne transmission, which happens when contaminated food is consumed, and direct transmission among humans from both infected and deceased individuals. The resulting NiV epidemic model consists of nine equations that capture the dynamical aspects of various population groups. The representation of virus shedding by flying foxes at any given time is denoted by the variable \(V(t)\). The flying fox population is divided into susceptible (\(S_f\)) and infected (\(I_f\)) groups. Flying foxes carrying the virus can infect humans. The human population is further divided into six sub-groups: susceptible humans, represented as \(S_h\), vaccinated humans, represented as \(V_h\), infected humans, represented as \(I_h\), treated humans, represented as \(T_h\), recovered humans, represented as \(R_h\), and deceased human bodies, represented as \(D_h\). The total flying fox population is represented as \(N_f = S_f + I_f\), and the total human population is represented as \(N_h = S_h + V_h + I_h + T_h + R_h\). The dynamics in each class can be described as follows.

Dynamics of flying foxes

The recruitment rate of \(S_f\) is denoted as \(\Lambda _{f}\), while their natural death rate is represented by \(d_{f}\). When \(S_f\) interacts with the Nipah virus, they have a chance of becoming infected at a rate of \(\beta _{1}\), subsequently moving to the infectious class. The infectious flying foxes pass away at a rate of \(d_{f}\). Thus,

$$\begin{aligned} S_{f}^{'}\left( t\right) =\Lambda _{f}-\frac{\beta _{1}V}{N_{f}}S_{f}-d_{f}S_{f}, \end{aligned}$$
(1)

and

$$\begin{aligned} I_{f}^{'}\left( t\right) =\frac{\beta _{1}V}{N_{f}}S_{f}-d_{f}I_{f}. \end{aligned}$$
(2)

Dynamics of the nipah viral concentration

To better understand the transmission dynamics of viruses among flying foxes we construct the following equation

$$\begin{aligned} V^{'}\left( t\right) =pI_{f}-\theta V, \end{aligned}$$
(3)

where p and \(\theta\) are the virus shedding and decay rates respectively.

Dynamics of human population

The transmission of the Nipah virus occurs in three ways: through contaminated food (at a rate of \(\beta _{2}\)), through direct contact between infected and susceptible individuals (at a rate of \(\beta _{3}\)), and through touching the bodies of people who have been infected and have died (at a rate of \(\beta _{4}\), with a fraction of \(\kappa\) indicating those dead bodies not properly handled leading to the spread of NiV). The force of infection can be calculated by taking into account all three transmission rates. Thus is we have:

$$\begin{aligned} \lambda _{h}=\frac{\beta _{2}V+\beta _{3}I_{h}+\beta _{4}\kappa D_{h}}{N_{h}}. \end{aligned}$$
(4)

The rate at which the human population is recruited is denoted by \(\Lambda _{h}\). The susceptible population increases at a rate of \(\gamma\), which represents waning of immunity. Furthermore, vaccinated individuals rejoin the susceptible class at a rate of \(\zeta\) due to vaccine wanning immunity. Conversely, the susceptible population decreases due to three factors: interaction with contaminated food and infected humans, represented by the force of infection \(\lambda _{h}\); vaccination at the rate \(\xi\); and the natural death rate \(d_{h}\). Thus, we have:

$$\begin{aligned} S_{h}^{'}\left( t\right) =\Lambda _{h}-\frac{(\beta _{2}V+\beta _{3}I_{h}+\beta _{4}\kappa D_{h})}{N_{h}}S_{h}-(d_{h}+\xi )S_{h}+\gamma R_{h}+\zeta V_{h}. \end{aligned}$$
(5)

The vaccinated human population increases as susceptible individuals join it at a rate of \(\xi .\) The population is reduced by natural death rates of \(d_h\), and due vaccine wanning immunity at the rate \(\zeta\).

$$\begin{aligned} V_{h}^{'}\left( t\right) =\xi S_{h}-(\zeta +d_{h})V_{h}. \end{aligned}$$
(6)

When susceptible individuals are infected with a disease, the number of infected individuals increases. This is due to the force of infection, denoted by \(\lambda _{h}\). However, the population of infected individuals decreases due to various factors such as recovery rate \(\alpha _{1}\), treatment rate \(\rho\), disease-related mortality \(d_{1}\), and natural mortality rate \(d_{h}\).

$$\begin{aligned} I_{h}^{'}\left( t\right) =\frac{(\beta _{2}V+\beta _{3}I_{h}+\beta _{4}\kappa D_{h})}{N_{h}}S_{h}-\left( \rho +\alpha _{1}+d_{1}+d_{h}\right) I_{h}. \end{aligned}$$
(7)

The infected people join treatment class at the flow rate \(\rho\). This class is reduced after getting recovery at a rate \(\alpha _{2}\) and natural mortality \(d_{h}\).

$$\begin{aligned} T_{h}^{'}\left( t\right) =\rho I_{h}-\left( \alpha _{2}+d_{h}\right) T_{h}. \end{aligned}$$
(8)

The recovered individuals increase through the induction of the infected and treated individuals at a steady influx rate of \(\alpha _{1}\) and \(\alpha _{2}\), respectively. Additionally, a decrease in the recovered population occurs due to natural death and loss of immunity, indicated by the rates \(d_{h}\) and \(\gamma\), respectively.

$$\begin{aligned} R_{h}^{'}\left( t\right) =\alpha _{1}I_{h}+\alpha _{2}T_{h}-\left( \gamma +d_{h}\right) R_{h}. \end{aligned}$$
(9)

The individuals who die due to NiV infection are added to the deceased class at a rate of \(d_{1}\). The deceased individuals are buried at a rate of \(\nu\).

$$\begin{aligned} D_{h}^{'}\left( t\right) =d_{1}I_{h}-\nu D_{h}. \end{aligned}$$
(10)

By combining the aforementioned differential equations, the dynamics of Nipah virus can be modeled by a system of nonlinear differential equations as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{f}^{'}\left( t\right) =\Lambda _{f}-\frac{\beta _{1}V}{N_{f}}S_{f}-d_{f}S_{f},\\ I_{f}^{'}\left( t\right) =\frac{\beta _{1}V}{N_{f}}S_{f}-d_{f}I_{f},\\ V^{'}\left( t\right) =pI_{f}-\theta V,\\ S_{h}^{'}\left( t\right) =\Lambda _{h}-\frac{(\beta _{2}V+\beta _{3}I_{h}+\beta _{4}\kappa D_{h})}{N_{h}}S_{h}-(d_{h}+\xi )S_{h}+\gamma R_{h}+\zeta V_{h},\\ V_{h}^{'}\left( t\right) =\xi S_{h}-(\zeta +d_{h})V_{h},\\ I_{h}^{'}\left( t\right) =\frac{(\beta _{2}V+\beta _{3}I_{h}+\beta _{4}\kappa D_{h})}{N_{h}}S_{h}-\left( \rho +\alpha _{1}+d_{1}+d_{h}\right) I_{h},\\ T_{h}^{'}\left( t\right) =\rho I_{h}-\left( \alpha _{2}+d_{h}\right) T_{h},\\ R_{h}^{'}\left( t\right) =\alpha _{1}I_{h}+\alpha _{2}T_{h}-\left( \gamma +d_{h}\right) R_{h},\\ D_{h}^{'}\left( t\right) =d_{1}I_{h}-\nu D_{h}, \end{array}\right. } \end{aligned}$$
(11)

where the initial conditions (ICs) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{f}(0)=S_{f}{}_{0}\ge 0,I_{f}(0)=I_{f}{}_{0}\ge 0,V(0)=V_{0}\ge 0,S_{h}(0)=S_{h}{}_{0}\ge 0,V_{h}(0)=V_{h0}\ge 0,\\ I_{h}(0)=I_{h}{}_{0}\ge 0,T_{h}(0)=T_{h}{}_{0}\ge 0,R_{h}(0)=R_{h}{}_{0}\ge 0,D_{h}(0)=D_{h}{}_{0}\ge 0. \end{array}\right. } \end{aligned}$$
(12)

Qualitative analysis of NiV model

Invariantly positive region

The region having biological feasibility for the problem (11) is shown in the following set

$$\begin{aligned} \varTheta =\varTheta _f\times \varTheta _h \subset \mathbb {R}_ + ^3 \times \mathbb {R}_ + ^6, \end{aligned}$$

where

$$\begin{aligned} \varTheta _f&=\left\{ \; {\left( {S_f,\;I_f,V}\right) \in \;\mathbb {R}_{+}^{3}:N_f=S_f+I_f=\frac{{\Lambda _f}}{{d_f}},V\le \frac{{p\Lambda _f}}{{\theta d_f}}}\right\} ,\\ \varTheta _h&=\left\{ {\left( {S_h,\;V_h,\;I_h,\;T_h,\;R_h,\;D_h}\right) \in \mathbb {R}_{+}^{6}:N_h=S_h+V_h+I_h+T_h+R_h\le \frac{{\Lambda _h}}{{d_h}},D_h\le \frac{{\Lambda _h {d_{1}}}}{{\nu d_h}}}\right\} . \end{aligned}$$

Theorem 1

The model (11) with the ICs defined in (12) has a positive invariant solution in \(\Theta =\Theta _{f}\times \Theta _{h}\).

Proof

It is easy to demonstrate that entire solutions originating from nonnegative ICs will also remain nonnegative \(\forall\) \(t > 0\). Furthermore, from the model (11), we proceed as follows

$$\begin{aligned} N_f^{'}(t)&= S_f^{'}(t) + I_f^{'}(t) , \\&= \Lambda _f - d _f N_f, \end{aligned}$$

alternatively,

$$\begin{aligned} N_f^{'}(t) + d_f N_f = \Lambda _f. \end{aligned}$$
(13)

Applying the Laplace transformation

$$\begin{aligned}&\mathcal {L}\left[ {N_f^{'}(t) + d _f N_f } \right] = \mathcal {L}\left[ {\Lambda _f } \right] , \\&sY(s) - N_f(0) + d_f Y(s) = \frac{\Lambda _f}{s}, \\&(s + d_f)Y(s) = N_{f0} + \frac{\Lambda _f}{s},\\&Y(s) = \frac{N_{f0}}{s + d_f} + \frac{\Lambda _f}{s(s + d_f)}. \end{aligned}$$

The inverse Laplace further gives the following form:

$$\begin{aligned} N_f(t) = \frac{\Lambda _f}{d_f} + \left( N_{f0} - \frac{\Lambda _f}{d_f}\right) e^{- d_f t}. \end{aligned}$$

We derive that \(N_f(t)\le \frac{\Lambda _f}{d_f}\), if \(N_f(0)\le \frac{\Lambda _f}{d_f}\), whenever \(t\longrightarrow \infty\). As a result, for \(t>0\), the NiV model (11) solution with ICs in \(\varTheta _f\) remains in \(\Theta _f\). A similar procedure leads to the fact that \(V(t) \le \frac{p \Lambda _f}{\theta d_f}\), \(N_h(t)\le \frac{\Lambda _h}{d_h}\) and \(D_h(t)\le \frac{d_1 \Lambda _h}{\nu d_h}\) as \(t>0\). Therefore, it is concluded that the region \(\varTheta\) posses positive invariantness property and consequently attracts all solutions of the system. \(\square\)

Investigation of equilibria and threshold parameter

The NiV epidemic model attains three equilibrium points. The infection-free equilibrium (IFE) is given as follows:

$$\begin{aligned} E^{0}=\left( S_{f}^{0},I_{f}^{0},V^{0},S_{h}^{0},V_{h}^{0},I_{h}^{0},T_{h}^{0},R_{h}^{0},D_{h}^{0}\right) =\left( {\frac{{\Lambda _{f}}}{{d_{f}}},0,0,\frac{\Lambda _h \left( d_h+\zeta \right) }{d_h \left( d_h+\zeta +\xi \right) },\frac{\xi \Lambda _h}{d_h \left( d_h+\zeta +\xi \right) },0,0,0,0}\right) . \end{aligned}$$
(14)

The threshold number, denoted as \(\mathcal {R}_{0}\), is derived using the technique presented in29, and given as follows.

$$\begin{aligned} \mathcal {R}_{0}=\max \left\{ {\mathcal {R}_{f}^{0},\mathcal {R}_{h}^{0}}\right\} =\max \left\{ {\mathcal {R}_{f}^{0},\mathcal {R}_{h_{1}}^{0}+\mathcal {R}_{h_{2}}^{0}}\right\} =\max \left\{ {\frac{p\beta _{1}}{{\theta d_{f}}},\frac{{\beta _{3}c_2}}{{c_{3}(c_2+\xi )}}+\frac{d_1\beta _{4}\kappa c_2}{\nu c_{3}(c_2+\xi )}}\right\} , \end{aligned}$$
(15)

where, \(c_{2}=(\zeta +d_{h})\) and \(c_{3}=(\rho +\alpha _{1}+d_{1}+d_{h})\).

Stability of the model

After applying the Jacobian method to the system (11), it is possible to confirm the local stability of IFE.

Theorem 2

For \(\mathcal {R}_{0}<1\), the equilibrium is locally asymptotically stable (LAS), while it is unstable otherwise.

Proof

At the infection-free equilibrium, the LAS can be examined by analyzing the Jacobian matrix of system (11). The corresponding Jacobian matrix is evaluated as follows:

$$\begin{aligned} J_9=\left( \begin{array}{ccccccccc} -\theta &{} 0 &{} p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\beta _1 &{} -d_f &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \beta _1 &{} 0 &{} -d_f &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\frac{\beta _2 c_2}{c_2+\xi } &{} 0 &{} 0 &{} -c_1 &{} \zeta &{} -\frac{\beta _3 c_2}{c_2+\xi } &{} 0 &{} \gamma &{} -\frac{\beta _4 c_2 \kappa }{c_2+\xi } \\ 0 &{} 0 &{} 0 &{} \xi &{} -c_2 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{\beta _2 c_2}{c_2+\xi } &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{\beta _3 c_2}{c_2+\xi }-c_3 &{} 0 &{} 0 &{} \frac{\beta _4 c_2 \kappa }{c_2+\xi } \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \rho &{} -c_4 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \alpha _1 &{} \alpha _2 &{} -c_5 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} d_1 &{} 0 &{} 0 &{} -\nu \end{array} \right) . \end{aligned}$$

The eigenvalue \(\lambda _{1}=-d_{f}\) is negative, so we have

$$\begin{aligned} J_8=\left( \begin{array}{ccccccccc} -\theta &{} p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \beta _1 &{} -d_f &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\frac{\beta _2 c_2}{c_2+\xi } &{} 0 &{} -c_1 &{} \zeta &{} -\frac{\beta _3 c_2}{c_2+\xi } &{} 0 &{} \gamma &{} -\frac{\beta _4 c_2 \kappa }{c_2+\xi } \\ 0 &{} 0 &{} \xi &{} -c_2 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{\beta _2 c_2}{c_2+\xi } &{} 0 &{} 0 &{} 0 &{} \frac{\beta _3 c_2}{c_2+\xi }-c_3 &{} 0 &{} 0 &{} \frac{\beta _4 c_2 \kappa }{c_2+\xi } \\ 0 &{} 0 &{} 0 &{} 0 &{} \rho &{} -c_4 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \alpha _1 &{} \alpha _2 &{} -c_5 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} d_1 &{} 0 &{} 0 &{} -\nu \end{array} \right) . \end{aligned}$$

Further, by row operation, we have

$$\begin{aligned} J_{8}=\left( \begin{array}{cccccccc} -\theta &{} p &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} a_{22} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -c_{1} &{} \zeta &{} -\beta _{3} &{} 0 &{} \gamma &{} -\beta _{4}\kappa \\ 0 &{} 0 &{} 0 &{} b_{44} &{} b_{45} &{} 0 &{} b_{47} &{} b_{48}\\ 0 &{} 0 &{} 0 &{} 0 &{} \beta _{3}-c_{3} &{} 0 &{} 0 &{} \beta _{4}\kappa \\ 0 &{} 0 &{} 0 &{} 0 &{} \rho &{} -c_{4} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} c_{75} &{} 0 &{} -c_{5} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} d_1 &{} 0 &{} 0 &{} -\nu \end{array}\right) , \end{aligned}$$

where \(a_{22}=\frac{\beta _{1}p-d_{f}\theta }{\theta },\) \(b_{44}=\frac{\xi \zeta -c_{1}c_{2}}{c_{1}},\) \(b_{45}=\frac{-\beta _{3}\xi }{c_{1}},\) \(b_{47}=\frac{\gamma \xi }{c_{1}},\) \(b_{48}=\frac{-\beta _{4}\xi \kappa }{c_{1}},\) \(c_{75}=\frac{\alpha _{1}c_{4}+\alpha _{2}\rho }{c_{4}}.\)    This implies that the eigenvalues i.e., \(\lambda _{2}=-\theta\), \(\lambda _{3}=-c_{1}\), \(\lambda _{4}=-c_{4}\) are also negatives.

To further evaluate, we will take the sub-matrix

$$\begin{aligned} J_{5}=\left( \begin{array}{ccccc} a_{22} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} b_{44} &{} b_{45} &{} b_{47} &{} b_{48}\\ 0 &{} 0 &{} \beta _{3}-c_{3} &{} 0 &{} \beta _{4}\kappa \\ 0 &{} 0 &{} c_{75} &{} -c_{5} &{} 0\\ 0 &{} 0 &{} d_1 &{} 0 &{} -\nu \end{array}\right) . \end{aligned}$$

The eigenvalues that are included in the Jacobian matrix \(J_{5}\), can be obtained by finding the roots of its characteristic equation. These eigenvalues correspond to the remaining eigenvalues of \(J_{9}\).

$$\begin{aligned} \lambda _{h}^{**5}+l _{1}\lambda _{h}^{**4}+l _{2}\lambda _{h}^{**3}+l _{3}\lambda _{h}^{**2}+l _{4}\lambda _{h}^{**}+l _{5}=0, \end{aligned}$$
(16)

where,

$$\begin{aligned} l _{1}&=\mathrm {c_{3}}(1-\mathcal {R}_{h1}^{0})+\mathrm {c_{5}}+{\nu }+d_{f}(1-\mathcal {R}_{f}^{0})+\frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}},\\ l _{2}&=c_{3}\nu (1-\mathcal {R}_{h}^{0})+c_{5}(\mathrm {c_{3}}(1-\mathcal {R}_{h1}^{0})+\nu )+\left\{ d_{f}(1-\mathcal {R}_{f}^{0})+\frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}}\right\} \{\mathrm {c_{3}}(1-\mathcal {R}_{h1}^{0})+\mathrm {c_{5}}+{\nu }\}\\&\quad + d_{f}(1-\mathcal {R}_{f}^{0})\left\{ \frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}}\right\} ,\\ l_{3}&=\left\{ d_{f}(1-\mathcal {R}_{f}^{0})+\frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}}\right\} \{c_{5}(c_{3}(1-\mathcal {R}_{h1}^{0})+\nu )+c_{3}\nu (1-\mathcal {R}_{h}^{0})\}\\&\quad +c_{3}c_{5}\nu (1-\mathcal {R}_{h}^{0})+ \left\{ \frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}} \right\} \{\mathrm {c_{3}}(1-\mathcal {R}_{h1}^{0})+c_{5}+\nu \}\{d_{f}(1-\mathcal {R}_{f}^{0})\},\\ l_{4}&=c_{3}c_{5}\nu \left\{ d_{f}(1-\mathcal {R}_{f}^{0})+\frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}} \right\} \{c_{3}(1-\mathcal {R}_{h}^{0})\}+\{d_{f}(1-\mathcal {R}_{f}^{0})\}\left\{ \frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}} \right\} \{c_{5}\mathrm {c_{3}}(1-\mathcal {R}_{h1}^{0})\\&\quad +\nu (c_{3}(1-\mathcal {R}_{h}^{0})+c_{5})\},\\ l _{5}&=c_{3}c_{5}\nu \{d_{f}(1-\mathcal {R}_{f}^{0})\} \left\{ \frac{\mathrm {c_{1}}\mathrm {c_{2}}-{\xi }{\zeta }}{\mathrm {c_{1}}} \right\} \{(1-\mathcal {R}_{h}^{0})\}. \end{aligned}$$

Clearly, all l_{i}, i=1,...5,  are positive if \(\mathcal {R}_{h}^{0}\). Hence the equilibrium is LAS if \(\mathcal {R}_{h}^{0}<1\). \(\square\)

Infected flying foxes-free equilibrium state

Theorem 3

In the NiV model (11), if \(\mathcal {R}_{0}>1\), \(\exists\) a unique infected flying-foxes free equilibrium (IFFE).

Proof

By solving Eq. (11) simultaneously for virus and human compartments, we obtain an expression for \(S_{f}=\frac{\Lambda _{f}}{d_{f}}\), \(I_{f}=0\), and \(V=0,\) the in terms of the IFFE point we have the following set

$$\begin{aligned} E_{h}^{*}=\left( \frac{{\Lambda _{f}}}{{d_{f}}},0,0,S_{h}^{*},V_{h}^{*},I_{h}^{*},T_{h}^{*},R_{h}^{*},D_{h}^{*}\right) , \end{aligned}$$
(17)

such that

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{h}^{*}=\frac{c_{2}c_{3}c_{4}c_{5}\Lambda _{h}}{c_{3}c_{4}c_{5}(c_{1}c_{2}-\zeta \xi )+c_{2}\lambda _{h}(c_{3}c_{4}c_{5}-\gamma (\alpha _{1}c_{4}+\alpha _{2}\rho ))},\\ V_{h}^{*}=\frac{\xi }{c_{2}}S_{h}^{*},\\ I_{h}^{*}=\frac{1}{c_{3}}\lambda _{h}^{*}S_{h}^{*},\\ T_{h}^{*}=\frac{\rho }{c_{3}c_{4}}\lambda _{h}^{*}S_{h}^{*},\\ R_{h}^{*}=\frac{(\alpha _{1}c_{4}+\alpha _{2}\rho )}{c_{3}c_{4}c_{5}}\lambda _{h}^{*}S_{h}^{*},\\ D_{h}^{*}=\frac{d_1}{\nu c_{3}}\lambda _{h}^{*}S_{h}^{*}, \end{array}\right. } \end{aligned}$$
(18)

where,

$$\begin{aligned} \lambda _{h}^{*}=\frac{\beta _{2}V^{*}+\beta _{3}I_{h}^{*}+\beta _{4}\kappa D_{h}^{*}}{N_{h}^{*}}. \end{aligned}$$
(19)

Further, putting (18) in (19), we obtain

$$\begin{aligned} \varrho _{1}\lambda _{h}^{*}+\varrho _{2}=0, \end{aligned}$$
(20)

where the coefficients are

$$\begin{aligned} \varrho _{1}= & {} c_{3}c_{4}c_{5}\nu \Lambda _{h}\left( \xi +(1-\mathcal {R}_{h}^{0})\right) ,\\ \varrho _{2}= & {} c_{2}\nu \Lambda _{h}\left( \alpha _{2}\rho +\alpha _{1}c_{4}+c_{5}\left( c_{4}+\rho \right) \right) . \end{aligned}$$

Hence, a unique IFFE point exists if \(\mathcal {R}_{h}^{0}>1\). \(\square\)

NiV-endemic equilibrium

From the NiV epidemic model (11) we obtain

$$\begin{aligned} E^{**}=\left( S_{f}^{**},I_{f}^{**},V^{**},S_{h}^{**},V_{h}^{**},I_{h}^{**},T_{h}^{**},R_{h}^{**},D_{h}^{**}\right) , \end{aligned}$$
(21)

such that

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{f}^{**}=\frac{\theta \Lambda _{f}^{**}}{p\beta _{1}},\\ I_{f}^{**}=\frac{\Lambda _{f}^{**}\left( p\beta _{1}-\theta d_{f}\right) }{p\beta _{1}d_{f}},\\ V^{**}=\frac{\Lambda _{f}^{**}\left( p\beta _{1}-\theta d_{f}\right) }{\beta _{1}\theta d_{f}},\\ S_{h}^{**}=\frac{c_{2}c_{3}c_{4}c_{5}\Lambda _{h}}{c_{3}c_{4}c_{5}(c_{1}c_{2}-\zeta \xi )+c_{2}\lambda _{h}(c_{3}c_{4}c_{5}-\gamma (\alpha _{1}c_{4}+\alpha _{2}\rho ))},\\ V_{h}^{**}=\frac{\xi }{c_{2}}S_{h}^{**},\\ I_{h}^{**}=\frac{1}{c_{3}}\lambda _{h}^{**}S_{h}^{**},\\ T_{h}^{**}=\frac{\rho }{c_{3}c_{4}}\lambda _{h}^{**}S_{h}^{**},\\ R_{h}^{**}=\frac{(\alpha _{1}c_{4}+\alpha _{2}\rho )}{c_{3}c_{4}c_{5}}\lambda _{h}^{**}S_{h}^{**},\\ D_{h}^{**}=\frac{d_1}{\nu c_{3}}\lambda _{h}^{**}S_{h}^{**}. \end{array}\right. } \end{aligned}$$
(22)

The force of infection term is given as follows

$$\begin{aligned} \lambda _{h}^{**}=\frac{\beta _{2}V^{**}+\beta _{3}I_{h}^{**}+\beta _{4}\kappa D_{h}^{**}}{N_{h}^{**}}. \end{aligned}$$
(23)

Further, putting (22) in (23), we obtain

$$\begin{aligned} \varpi _{1}\lambda _{h}^{**2}+\varpi _{2}\lambda _{h}^{**}+\varpi _{3}=0, \end{aligned}$$
(24)

where the coefficients are

$$\begin{aligned} \varpi _{2}= & {} \beta _{2} c_{3}c_{4}c_{5} \nu \Lambda _{f} (c_{1}c_{2}-\zeta \xi )(1-\mathcal {R}_{f}^{0}),\\ \varpi _{1}= & {} \beta _{2} c_{2} \nu \Lambda _{f} (1-\mathcal {R}_{f}^{0}) [c_{3}c_{4}c_{5}-\gamma \left( \alpha _{2}\rho +\alpha _{1}c_{4}\right) ] +\nu c_{3} c_{4}c_{5} \beta _{1} \Lambda _{h} (\xi + c_2) (1-\mathcal {R}_{h}^{0})\\ \varpi _{0}= & {} \beta _{1} c_{2} \Lambda _{h} [(\alpha _{1}c_{4}+\alpha _{2}\rho )+c_{5}\left( c_{4}+\rho \right) ]. \end{aligned}$$

Theorem about NVEE is developed as follows.

Theorem 4

  1. (i)

    A NVEE point \(E^{**}\) exists and will be unique if \(\varpi _2 < 0 \Longleftrightarrow \mathcal {R}_{f} \ge 1\).

  2. (ii)

    The point \(E^{**}\) will be unique if \((\varpi _1 < 0 \wedge \varpi _2=0)\) \(\vee\) \(\varpi ^2_1 - 4 \varpi _0 \varpi _2 =0\).

  3. (iii)

    The model has two NVEE if \(\varpi _1 < 0, \varpi _2 > 0\) and the discriminant is positive.

  4. (iv)

    An NVEE cannot be found anywhere else.

Proof

Following condition (i), there exists a unique NVEE for the said model. \(\square\)

Global asymptotically stability of the IFE

Theorem 5

For \(\mathcal {R}_{0}<1\), then the IFE of (11) is globally asymptotically stable (GAS).

Proof

In order to obtain the GAS of (11), a Lyapunov type function say \(\mathbb {F}\) is introduced.

$$\begin{aligned} \mathbb {F}=\mathbb {L}_{1}V+\mathbb {L}_{2}I_{f}+\mathbb {L}_{3}I_{h}+\mathbb {L}_{4}D_{h}, \end{aligned}$$

Later, we will consider the values of \(\mathbb {L}_{1},\mathbb {L}_{2},\mathbb {L}_{3}\) and \(\mathbb {L}_{4}\). Computing the time derivative of \(\mathbb {F}\) yields:

$$\begin{aligned} \mathbb {F}^{'}= & {} \mathbb {L}_{1}V^{'}+\mathbb {L}_{2}I_{f}^{'}+\mathbb {L}_{3}I_{h}^{'}+\mathbb {L}_{4}D_{h}^{'},\\ \mathbb {F}^{'}= & {} \mathbb {L}_{1}(pI_{f}-\theta V)+\mathbb {L}_{2}(\frac{\beta _{1}V}{N_{f}}S_{f}-d_{f}I_{f})+\mathbb {L}_{3}(\frac{(\beta _{2}V+\beta _{3}I_{h}+\beta _{4}\kappa D_{h})}{N_{h}}S_{h}-c_{3}I_{h})+\mathbb {L}_{4}(d_1I_{h}-\nu D_{h}),\\ \mathbb {F}^{'}\le & {} [-\mathbb {L}_{1}\theta +\mathbb {L}_{2}\beta _{1}+\mathbb {L}_{3}\beta _{2}]V+[\mathbb {L}_{1}p-\mathbb {L}_{2}d_{f}]I_{f}+[\mathbb {L}_{3}(\beta _{3}-c_{3})+\mathbb {L}_{4}d_1]I_{h}+[\mathbb {L}_{3}\beta _{4}\kappa -\mathbb {L}_{4}\nu ]D_{h}, \end{aligned}$$

Since \(S_{f}\le N_{f}\) and \(S_{h}\le N_{h}.\)

Setting the non-negative values of \(\mathbb {L}_{1}=\frac{\beta_2\mathbb {L}_{3}+\beta_1\mathbb {L}_{2}}{\theta},~~\mathbb {L}_{2}=\frac{p\mathbb {L}_{1}}{d_f},~~\mathbb {L}_{3}=\frac{c_3 \nu \left(c_2+\xi \right)-c_2 \left(\beta _3 \nu +\beta _4 d_1 \kappa \right)}{c_3 \nu -\left(\beta _3 \nu +\beta _4 d_1 \kappa \right)},\) and \(~~\mathbb {L}_{4}=\frac{\beta _4 \kappa \left(c_3 \nu \left(c_2+\xi \right)-c_2 \left(\beta _3 \nu +\beta _4 d_1 \kappa \right)\right)}{\nu \left(c_3 \nu -\left(\beta _3 \nu +\beta _4 d_1 \kappa \right)\right)},\) we get

$$\begin{aligned} \mathbb {F}^{'}\le & {} c_3 \left(c_2+\xi \right) \left(\frac{c_2 \left(\beta _3 \nu +\beta _4 d_1 \kappa \right)}{c_3 \nu \left(c_2+\xi \right)}-1\right)I_{h},\\ \mathbb {F}^{'}\le & {} c_3 \left(c_2+\xi \right)(\mathcal {R}_{h}^{0}-1)I_{h}. \end{aligned}$$

If \(\mathcal {R}_{f}^{0}<1\) and \(\mathcal {R}_{h}^{0}<1\), i.e., if the value of \(\mathcal {R}_{0}\) is less than one then it can be observed that the derivative of the Lyapunov function \(\mathbb {F}^{'}\), is negative. Therefore, it can be claimed that the IFE of the NiV epidemic model is GAS. \(\square\)

Application to the outbreak reported in Bangladesh during 2001–2015

Epidemiology and outbreak of NiV in Bangladesh

NiV has a considerable influence on public health in Bangladesh. During 2001 to 2015 multiple outbreaks have been reported in Bangladesh. In Bangladesh, NiV outbreaks have occurred primarily in the central and northwestern regions of the country, particularly in the districts of Rajshahi, Naogaon, and Faridpur. The disease primarily affects individuals involved in the farming and harvesting of date palm sap, as well as those who come into contact with infected animals, particularly fruit bats (the natural reservoir of the virus), and contaminated food or beverages. NiV infection in Bangladesh typically presents with a range of symptoms, including fever, headache, dizziness, respiratory distress, vomiting, and altered consciousness. In severe cases, it can progress to encephalitis (inflammation of the brain) and lead to coma or death. The disease has a high mortality rate, ranging from 40% to 75% in reported outbreaks. Efforts to control NiV infection in Bangladesh have focused on surveillance and early detection of cases, as well as public health interventions to limit transmission. These interventions include the culling of infected animals, quarantine measures, and public awareness campaigns to educate communities about the risks of the disease and how to prevent transmission. Research efforts have also been directed towards understanding the ecology of the NiV, including its transmission dynamics between bats, intermediate hosts (such as pigs), and humans along with the vaccines and antiviral treatments30,31. The cumulative cases are displayed in Fig. 1.

Figure 1
figure 1

Reported cumulative confirmed cases during from 2001-2015 outbreaks occurred in Bangladesh.

Full size image

Clinical description and estimation procedure of parameters

Some of the NiV epidemic model embedded parameters are estimation from the clinical facts during 2001-2015 outbreaks occurred in Bangladesh. While the rest are considered from the references mentioned in the Table 1. The life expectancy of the population in Bangladesh is reported to be 73.57 years32. Consequently, the natural death rate, denoted as \(d_h\), is calculated as \(d_h=\frac{1}{365 \times 73.57}\) per day. The infection induced rate concern to NiV in Bangladesh is notably high, between 73% to 77%, while the reported recovery rate stands at 22.457%33. Consequently, the NiV-induced death rate is estimated to be approximately \(d_1=0.77\), and the recovery rate is estimated as \(\alpha _1=0.22457\)33. \(\Lambda _{h}\) is determined using the fact \(\Lambda _{h}=N_h(0) \times d_h\), where \(N_h(0)\) represents the total population size in Bangladesh during 201534. Following same procedure, the rest of parameters can be estimated utilizing their clinical facts and reported cases as summarized in Table 1.

Model validation with real data

This section presents the fitting procedure of the proposed model with real data set given in34. A robust method called the stranded nonlinear least squares regression minimization procedure is utilized for the fitting purpose. This approach is employed to identify the optimum parameter’ values minimizing the error between the model simulated data and the reported data, as detailed in35. The minimization process is executed using MATLAB version R2020b, utilizing the “lsqcurvefit” algorithm based on the following relation

$$\begin{aligned} \hat{\Theta }=argmin\sum _{\jmath =1}^{n}{({H_I}_{t_\jmath }-\overline{H_I}_{t_\jmath })}^2, \end{aligned}$$

where, \(\overline{H}_I{t_\jmath }\) denotes real data and \(H_I{t_\jmath }\) are the simulated cases at temporal point \(t_\jmath ,\) whereas n denotes the entire data points. The cumulative cases are displayed in Fig. 1 while the simulated fitted curve is depicted in Fig. 2.

Figure 2
figure 2

Model fitting curve (blue solid plot) versus real data (stars red).

Full size image
Table 1 Description of the used parameters in NiV model.
Full size table

Sensitivity of the threshold parameters

This section presents a normalized sensitivity analysis, one of the useful tools in epidemiology and can suggest optimal control measures for an infection outbreak. We perform this analysis for various model parameters versus the reproduction number using the parametric technique40. The purpose of sensitivity indices is to show the impact level of corresponding parameters on the infection incidence and control. The following definition is taken into account for the aforementioned purpose.

Definition 1

The procedure to evaluated the normalized forward sensitivity index is given by the following formula

$$\begin{aligned} \mathbb {Y}{}_{x}=\frac{x}{\mathcal {R}_{0}}\frac{\partial \mathcal {R}_{0}}{\partial x}. \end{aligned}$$
(25)

Table 2 shows the normalized sensitivity index for \(\mathcal {R}_{h}^{0}\) and \(\mathcal {R}_{f}^{0}\) with respect to the model parameters, using the procedure applied on (25). The sensitivity index values indicate whether a parameter has a positive or negative effect on the basic reproduction number. This helps in understanding the direct and indirect relationships between the model parameters and the basic reproduction number.

The parameters \(\beta _{1}, p, \beta _{3}, \beta _{4}\) and \(\kappa\) have positive indices, indicating that they have a direct impact on \(\mathcal {R}_{h}^{0}\) and \(\mathcal {R}_{f}^{0}\). This means that when these parameters increase, \(\mathcal {R}_{h}^{0}\) and \(\mathcal {R}_{f}^{0}\) values will increase too. Conversely, the parameters \(d_f, \theta , d_h, \alpha _1, \nu\), and \(d_1\) have negative indices, which suggest that they have an inverse relationship with the basic reproduction number. Therefore, if we increase these parameters, \(\mathcal {R}_{h}^{0}\) and \(\mathcal {R}_{f}^{0}\) values will decrease.

Furthermore, Fig. 3 shows the sensitivity indices of the model parameters as a bar graph. This graph emphasizes how crucial it is to increase treatment strategies, decrease effective contact rates between vulnerable and infected populations, and improve vaccine efficacy in order to lower the incidence of disease.

Table 2 Sensitivity indices of model parameters.
Full size table
Figure 3
figure 3

Bar plot showing the sensitivity indices for the NiV epidemic model.

Full size image

Formulation of the optimal control NiV model

We introduced six control variables in the NiV model presented in (11) for the population-level mitigation of the infection. These six control measures, namely \(u_1, u_2, u_3, u_4, u_5,\) and \(u_6\), have been implemented in the model (11) to ensure its effectiveness. Each control measure plays a significant role in achieving our goals, and we have provided a brief overview of their roles below: The control variables implemented in the NiV model serve specific purposes to control the disease incidence at the population level. The variable \(u_1\) minimizes the transmission of viruses between susceptible flying foxes by restricting their movement with protective coverings. The variable \(u_2\) aims to increase the mortality rate of infected Pteropus flying foxes by targeted culling particularly in areas where outbreaks have been identified. The variable \(u_3\) manages the zoonotic transmission of viruses from infected flying foxes to humans through food contamination. The variable \(u_4\) controls the transmission of infectious diseases by managing human contact with infected individuals and contaminated cadavers through personal protections. The variable \(u_5\) focuses on implementing strategies to increase the number of individuals who have received NiV vaccinations. The variable \(u_6\) measures the effort required to provide health treatment to those who are infected.

The structure of system (11) by incorporating the above control variables is given below:

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{f}^{'}\left( t\right) =\Lambda _{f}-\frac{\beta _{1}V(1-u_{1})}{N_{f}}S_{f}-d_{f}S_{f},\\ I_{f}^{'}\left( t\right) =\frac{\beta _{1}V(1-u_{1})}{N_{f}}S_{f}-(d_{f}+u_{2})I_{f},\\ V^{'}\left( t\right) =pI_{f}-\theta V,\\ S_{h}^{'}\left( t\right) =\Lambda _{h}-\frac{\beta _{2}V(1-u_{3})}{N_{h}}S_{h}-\frac{(\beta _{3}I_{h}+\beta _{4}\kappa D_{h})(1-u_{4})}{N_{h}}S_{h}-(d_{h}+u_{5})S_{h}+\gamma R_{h}+\zeta V_{h},\\ V_{h}^{'}\left( t\right) =u_{5}S_{h}-(\zeta +d_{h})V_{h},\\ I_{h}^{'}\left( t\right) =\frac{\beta _{2}V(1-u_{3})}{N_{h}}S_{h}+\frac{(\beta _{3}I_{h}+\beta _{4}\kappa D_{h})(1-u_{4})}{N_{h}}S_{h}-\left( u_{6}+\alpha _{1}+d_{1}+d_{h}\right) I_{h},\\ T_{h}^{'}\left( t\right) =u_{6}I_{h}-\left( \alpha _{2}+d_{h}\right) T_{h},\\ R_{h}^{'}\left( t\right) =\alpha _{1}I_{h}+\alpha _{2}T_{h}-\left( \gamma +d_{h}\right) R_{h},\\ D_{h}^{'}\left( t\right) =d_{1}I_{h}-\nu D_{h}, \end{array}\right. } \end{aligned}$$
(26)

with the ICs stated in (12). The aim of optimal control problem is to reduce the density of infected flying foxes and infected humans in class \(I_f\) and \(I_h\), respectively, while maximizing the the vaccinated and under treatment humans. In order to accomplish this, we have formulated the following objective functional:

$$\begin{aligned}&J(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})=\int ^{T}_{0}(A_{1}I_{f}+A_{2}V+A_{3}I_{h}\nonumber \\&\quad +\frac{1}{2}(a_{1}u_{1}^{2}+a_{2}u_{2}^{2}+a_{3}u_{3}^{2}+a_{4}u_{4}^{2}+a_{5}u_{5}^{2}+a_{6}u_{6}^{2}))dt, \end{aligned}$$
(27)

subject to problem (26). In the objective functional (27). The constants \(A_1, A_2, A_3\) are associated weight constants while \(a_1, a_2, a_3, a_4, a_5,\) and \(a_6\) represent the associated cost factors. The final step size is represented by T41. Our main goal is to find the optimal controls for \(u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*},u_{5}^{*}\) and \(u_{6}^{*}\), so that we can achieve our objective.

$$\begin{aligned} J(u_{1}^{*}, u_{2}^{*}, u_{3}^{*},u_{4}^{*},u_{5}^{*},u_{6}^{*})=\text {min}\{J(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6}),(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6}){\in }U\}. \end{aligned}$$
(28)

The system described by Eq. (26) must satisfy certain constraints, and the control set is stated as follows:

$$\begin{aligned} U=\{(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})|u_{i}(t)\text { is Lebesgue' Measurable on }[0,1],i=1,2,3,4,5,6\}. \end{aligned}$$
(29)

To solve an optimum control problem, we use Pontryagin’s Principle42. This principle helps us formulate the necessary conditions and solutions for the problem. To begin solving the optimal problem, we focus on the Lagrangian and Hamiltonian for Eqs. (26) to (28). The Lagrangian for the optimal problem is defined as follows:

$$\begin{aligned} L=A_{1}I_{f}+A_{2}V+A_{3}I_{h}+\frac{1}{2}(a_{1}u_{1}^{2}+a_{2}u_{2}^{2}+a_{3}u_{3}^{2}+a_{4}u_{4}^{2}+a_{5}u_{5}^{2}+a_{6}u_{6}^{2}). \end{aligned}$$
(30)

Our goal is to find the minimum value of the Lagrangian L mentioned above. To achieve this, we introduce the Hamiltonian function \(\mathbb {H}\) defined as follows:

$$\begin{aligned} \mathbb {H}=L+\lambda _{1}\frac{dS_{f}}{dt}+\lambda _{2}\frac{dI_{f}}{dt}+\lambda _{3}\frac{dV}{dt}+\lambda _{4}\frac{dS_{h}}{dt}+\lambda _{5}\frac{dV_{h}}{dt}+\lambda _{6}\frac{dI_{h}}{dt}+\lambda _{7}\frac{dT_{h}}{dt}+\lambda _{8}\frac{dR_{h}}{dt}+\lambda _{9}\frac{dD_{h}}{dt}. \end{aligned}$$
(31)

\(\mathbb {H}\) is associated with the adjoint variables \(\lambda _{1},\ldots ,\lambda _{9}\). In the next step, we will demonstrate that an optimal control exists for system (26).

Existence of the optimal control problem

To establish the existence of the optimal control problem, we utilize the procedure outlined in43, along with the method employed by Ngina et al. in44. We then present the following result.

Theorem 6

Consider the objective function as define above

$$\begin{aligned} J(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})=\int _{0}^{T}(A_{1}I_{f}+A_{2}V+A_{3}I_{h}+\frac{1}{2}(a_{1}u_{1}^{2}+a_{2}u_{2}^{2}+a_{3}u_{3}^{2}+a_{4}u_{4}^{2}+a_{5}u_{5}^{2}+a_{6}u_{6}^{2}))dt, \end{aligned}$$

corresponding to state and controls variables mentioned in the system (26) and satisfies the ICs

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{f}(0)=S_{f}{}_{0}\ge 0,I_{f}(0)=I_{f}{}_{0}\ge 0,V(0)=V_{0}\ge 0,S_{h}(0)=S_{h}{}_{0}\ge 0,V_{h}(0)=V_{h0}\ge 0,\\ I_{h}(0)=I_{h}{}_{0}\ge 0,T_{h}(0)=T_{h}{}_{0}\ge 0,R_{h}(0)=R_{h}{}_{0}\ge 0,D_{h}(0)=D_{h}{}_{0}\ge 0. \end{array}\right. } \end{aligned}$$

then there exists optimal controls \((u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*},u_{5}^{*},u_{6}^{*})\) such that

$$\begin{aligned} J(u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*},u_{5}^{*},u_{6}^{*})=\text {min}\{J(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})|(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6}){\in }U\}. \end{aligned}$$

Proof

In order to establish the existence of the said problem, we need to satisfy the following steps:

  1. (i)

    The control set U paired with each state variable equation is not empty. This condition is met as all control and state variables within U are non-empty and non-negative, and \(u_{i},i=1,2,3,4,5,6\), is a Lebesque integrable function on the interval [0, T].

  2. (ii)

    The control set is both convex as well as closed. This has been demonstrated using the methodology outlined by Ngina et al.44). Initially, we represent the elements U in the following vector form.

    $$\begin{aligned} \hat{U}=(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6}), for 0 \le u_{1},u_{2},u_{3},u_{4},u_{5},u_{6} \le 1. \end{aligned}$$
    (32)

To prove the convexity of set U, let’s consider constants \(\varepsilon =\varepsilon _{1},\varepsilon _{2},\varepsilon _{3},\varepsilon _{4},\varepsilon _{5},\varepsilon _{6}\) that belong to the control set U, with the condition \(0 \le \varepsilon _{1},\varepsilon _{2},\varepsilon _{3},\varepsilon _{4},\varepsilon _{5},\varepsilon _{6} \le 1\).

We aim to prove that the equation

$$\begin{aligned} \omega =\phi U+(1-\phi )\varepsilon , for 0\le \phi \le 1 \end{aligned}$$

is a part of the control set U. Therefore, our objective is to demonstrate that

$$\begin{aligned} \omega&=\phi (u_{1},u_{2},u_{3},u_{4},u_{4},u_{5},u_{6})+(1-\phi )(\varepsilon _{1},\varepsilon _{2},\varepsilon _{3},\varepsilon _{4},\varepsilon _{5},\varepsilon _{6}),\nonumber \\&=(\phi u_{1}+(1-\phi )\varepsilon _{1},\phi u_{2}+(1-\phi )\varepsilon _{2},\phi u_{3}+(1-\phi )\varepsilon _{3},\phi u_{4}+(1-\phi )\varepsilon _{4},\nonumber \\&\quad \phi u_{5}+(1-\phi )\varepsilon _{5},\phi u_{6}+(1-\phi )\varepsilon _{6}),\nonumber \\&=(\omega _{1},\omega _{2},\omega _{3},\omega _{4},\omega _{5},\omega _{6}), \end{aligned}$$
(33)

where, \(\omega _{1}=\phi u_{1}+(1-\phi )\varepsilon _{1}\) , is within the interval [0, 1], hence, \(0\le \omega _{1}\le 1\).

The same applies for all \(\omega _{2},\omega _{3},\omega _{4},\omega _{5},\omega _{6}\). Hence, the vector \(\omega =(\omega _{1},\omega _{2},\omega _{3},\omega _{4},\omega _{5},\omega _{6})\) fulfills condition (32) for convexity, establishing the convex and closed nature of the control set U.

  1. (iii)

    The boundedness of each right-hand side of (26) is a linear function of U varying with time and state variables. To establish this, we are employing the approach introduced by44,45. Let

    $$\begin{aligned} \dot{\Upsilon }=W\Upsilon +N(\Upsilon ), \end{aligned}$$
    (34)

    where \(\Upsilon =(S_{f},I_{f},V,S_{h},V_{h},I_{h},T_{h},R_{h},D_{h})^{T},\)

    $$\begin{aligned} W=\left[ \begin{array}{ccccccccc} -d_{f} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} -d_{f} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -\theta &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -d_{h} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} -d_{h} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -d_{h} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -d_{h} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -d_{h} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\nu \end{array}\right] \end{aligned}$$
    (35)

    and

    $$\begin{aligned} N(\Upsilon )=\left[ \begin{array}{c} \Lambda _{f}-\frac{\beta _{1}V(1-u_{1})}{N_{f}}S_{f}\\ \\ \frac{\beta _{1}V(1-u_{1})}{N_{f}}S_{f}-u_{2}I_{f}\\ \\ pI_{f}\\ \\ \Lambda _{h}-\frac{\beta _{2}V(1-u_{3})}{N_{h}}S_{h}-\frac{(\beta _{3}I_{h}+\beta _{4}\kappa D_{h})(1-u_{4})}{N_{h}}S_{h}-u_{5}S_{h}+\gamma R_{h}+\zeta V_{h}\\ \\ u_{5}S_{h}-\zeta V_{h}\\ \\ \frac{\beta _{2}V(1-u_{3})}{N_{h}}S_{h}+\frac{(\beta _{3}I_{h}+\beta _{4}\kappa D_{h})(1-u_{4})}{N_{h}}S_{h}-\left( u_{6}+\alpha _{1}+d_{1}\right) I_{h}\\ \\ u_{6}I_{h}-\alpha _{2}T_{h}\\ \\ \alpha _{1}I_{h}+\alpha _{2}T_{h}-\gamma R_{h}\\ \\ d_{1}I_{h} \end{array}\right] . \end{aligned}$$
    (36)

    Representing

    $$\begin{aligned} G(\Upsilon )=W\Upsilon +N(\Upsilon ), \end{aligned}$$
    (37)

    the second term, \(N(\Upsilon )\) in Eq. (37) satisfies

    $$\begin{aligned} \begin{array}{ll} |N(\Upsilon _{1})-N(\Upsilon _{2})| &{} \le g_{1}|S_{f1}-S_{f2}|+g_{2}|I_{f1}-I_{f2}|+g_{3}|V_{1}-V_{2}|+g_{4}|S_{h1}-S_{h2}|+g_{5}|V_{h1}-V_{h2}|\\ \\ &{}\quad +g_{6}|I_{h1}-I_{h2}|+g_{7}|T_{h1}-T_{h2}|+g_{8}|R_{h1}-R_{h2}|+g_{9}|D_{h1}-D_{h2}|\\ \\ &{} \le g[|S_{f1}-S_{f2}|+|I_{f1}-I_{f2}|+|V_{1}-V_{2}|+|S_{h1}-S_{h2}|+|V_{h1}-V_{h2}|\\ \\ &{}\quad +|I_{h1}-I_{h2}|+|T_{h1}-T_{h2}|+|R_{h1}-R_{h2}|+|D_{h1}-D_{h2}|], \end{array} \end{aligned}$$
    (38)

    where

    $$\begin{aligned} \Upsilon _{1}=(S_{f1},I_{f1},V_{1},S_{h1},V_{h1},I_{h1},T_{h1},R_{h1},D_{h1}), \Upsilon _{2}=(S_{f2},I_{f2},V_{2},S_{h2},V_{h2},I_{h2},T_{h2},R_{h2},D_{h2}) \end{aligned}$$

    and g is an independent constant such that

$$\begin{aligned} g=\text {max}(g_{i},i=1,\cdots ,9). \end{aligned}$$

Also,

$$\begin{aligned}{}[G(\Upsilon _{1})-G(\Upsilon _{2})]\le g|\Upsilon _{1}-\Upsilon _{2}|, where \;\;g=\sum _{i=1}^{9}g_{i}+||G||\le \infty . \end{aligned}$$

The function \(G(\Upsilon )\) is uniformly Lipschitz continuous, given the definitions of the control variables \(u_{1}(t),u_{2}(t),u_{3}(t),u_{4}(t),u_{5}(t),u_{6}(t)\) and the constraints on the state variables;

$$\begin{aligned} (S_{f}>0,I_{f}\ge 0,V\ge 0,S_{h}\ge 0,V_{h}\ge 0,I_{h}\ge 0,T_{h}\ge 0,R_{h}\ge 0,D_{h}\ge 0), \end{aligned}$$

Consequently, the solution of the system (26) exists, thereby concluding the proof third condition.

  1. (iv)

    The integrand in (27) provided by

    $$\begin{aligned} \mathcal {P}=A_{1}I_{f}+A_{2}V+A_{3}I_{h}+\frac{1}{2}(a_{1}u_{1}^{2}+a_{2}u_{2}^{2}+a_{3}u_{3}^{2}+a_{4}u_{4}^{2}+a_{5}u_{5}^{2}+a_{9}u_{6}^{2}) \end{aligned}$$
    (39)

    exhibits convexity with respect to U. To establish this property, we employ the Hessian matrix method, defined as below:

Definition 6.1

Given a function \(\mathcal {V}(y_{1},y_{2},y_{3},\ldots ,y_{n})\), of several variables, then \(\mathcal {V}\), will be convex if and only if the Hessian matrix, \(H_{m}\) is such that

$$\begin{aligned} H_{m}(y)=\left[ \frac{\partial ^{2}\mathcal {V}}{\partial y_{i}\partial y_{j}}\right] \ge 0,\forall y\ne 0, \end{aligned}$$

and it is considered to be concave if and only if

$$\begin{aligned} H_{m}(y)=\left[ \frac{\partial ^{2}\mathcal {V}}{\partial y_{i}\partial y_{j}}\right] \le 0,\forall y\ne 0. \end{aligned}$$

So let

$$\begin{aligned} \mathcal {P}_{i}=\frac{1}{2}(a_{1}u_{1}^{2}+a_{2}u_{2}^{2}+a_{3}u_{3}^{2}+a_{4}u_{4}^{2}+a_{5}u_{5}^{2}+a_{6}u_{6}^{2}), \end{aligned}$$

where \(\mathcal {P}_{i}\in \mathcal {P},\) the Hessian Matrix for \(\mathcal {P}_{i}\) is given by

$$\begin{aligned} H_{m}=\left[ \begin{array}{cccccc} a_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} a_{2} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} a_{3} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} a_{4} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} a_{5} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} a_{6} \end{array}\right] \ge 0,\text {for} \;a_{1},a_{2},a_{3},a_{4},a_{5},a_{6}\ge 0. \end{aligned}$$
(40)

It can be observed that \(\mathcal {P}_{i}\) is a convex function in the domain U. If \(\mathcal {P}_{i}\in \mathcal {P}\) is convex in U, then it implies that \(\mathcal {P}\) is also convex in U and satisfies condition (iv).

  1. (xxii)

    Additionally, there exist some constants \(n_{1}\), \(n_{2}> 0\), and \(n_{3}> 1\), such that the integrand of (39) is both convex and bounded by

    $$\begin{aligned} \mathcal {P}(t,S_{f},I_{f},V,S_{h},V_{h},I_{h},T_{h},R_{h},D_{h},u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})\le n_{2}-\frac{n_{1}}{2}\left( \sum _{i=1}^{6}|u_{i}|^{2}\right) ^{\frac{n_{3}}{2}}. \end{aligned}$$

From (27), we proceed as

$$\begin{aligned} J\left( u_{1}(t),u_{2}(t),u_{3}(t),u_{4}(t),u_{5}(t),u_{6}(t)\right) =A_{1}I_{f}+A_{2}V+A_{3}I_{h}+\frac{1}{2}\left( \sum _{i=1}^{6}a_{i}u_{i}^{2}\right) , \end{aligned}$$

then,

$$\begin{aligned} J\left( u_{1}(t),u_{2}(t),u_{3}(t),u_{4}(t),u_{5}(t),u_{6}(t)\right) \le A_{1}I_{f}+A_{2}V+A_{3}I_{h}+\sum _{i=1}^{6}a_{i}u_{i}^{2}. \end{aligned}$$
(41)

Letting \(a=\text {max}(a_{1},a_{2},a_{3},a_{4},a_{5},a_{6})\) such that

$$\begin{aligned} J\left( u_{1}(t),u_{2}(t),u_{3}(t),u_{4}(t),u_{5}(t),u_{6}(t)\right) \le A_{1}I_{f}+A_{2}V+A_{3}I_{h}+a\sum _{i=1}^{6}u_{i}^{2}, \end{aligned}$$
(42)

this means that

$$\begin{aligned} A_{1}I_{f}+A_{2}V+A_{3}I_{h}+\sum _{i=1}^{6}a_{i}u_{i}^{2}\le n_{2}+n_{1}\sum _{i=1}^{6}|u_{i}|^{2}, \end{aligned}$$
(43)

where \(n_{2}\) based on the upper bound on \(I_{f},V,I_{h}\) and \(n_{1}>0\) since \(a_{i}>0\) for \(i=1,\cdots ,6\). Therefore, Eq. (42) can be revised as

$$\begin{aligned} J(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})\le n_{2}+n_{1}(u_{1},u_{2},u_{3},u_{4},u_{5},u_{6})^{2}. \end{aligned}$$
(44)

Now, from Eq. (44), it is observed that \(n_{1},n_{2}>0\), and \(n_{3}=2>1\). Finally, we conclude that there must exists an optimal control variables \(u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*},u_{5}^{*},u_{6}^{*}\). This completes the proof. \(\square\)

$$\begin{aligned} {\left\{ \begin{array}{ll} z^{'}=\frac{\partial {\mathbb {H}}(t,z,u,\lambda )}{\partial \lambda },\\ 0=\frac{\partial {\mathbb {H}}(t,z,u,\lambda )}{\partial u},\\ \lambda ^{'}=\frac{\partial {\mathbb {H}}(t,z,u,\lambda )}{\partial z}. \end{array}\right. } \end{aligned}$$
(45)

To obtain the necessary results, we use the above described conditions as follow.

Theorem 7

Let \(S_{f}^{*}\), \(I_{f}^{*}\), \(V^{*}\), \(S_{h}^{*}\), \(V_{h}^{*}\), \(I_{h}^{*}\), \(T_{h}^{*}\), \(R_{h}^{*}\), and \(D_{h}^{*}\) represent the state solutions associated with the optimal control measures \(u_{1}^{*}\), \(u_{2}^{*}\), \(u_{3}^{*}\), \(u_{4}^{*}\), \(u_{5}^{*}\), and \(u_{6}^{*}\) for the optimum control system stated in (26) and (27). Then, we find the adjoint variables \(\lambda _{1}, \ldots , \lambda _{9}\) that satisfy:

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda _{1}^{'} =d_f\lambda _{1}+(\lambda _{2}-\lambda _{1})\frac{S_f V\beta _1(1-u_1)}{N_f^2}+(\lambda _{1}-\lambda _{2})\frac{V\beta _1(1-u_1)}{N_f},\\ \lambda _{2}^{'}=-A_3+(\lambda _6-\lambda _7)u_6+(\lambda _6-\lambda _8)\alpha _1-\lambda _9(d_1+d_h)+(\lambda _6-\lambda _4) \frac{S_hI_h\beta _2(1-u_3)}{N_h^2}\\ +(\lambda _4-\lambda _6)\frac{(S_hI_h)\beta _2(1-u_3)}{N_h} +(\lambda _4-\lambda _6)\frac{S_h\beta _3(1-u_4)}{N_h}+(\lambda _6-\lambda _4)\frac{S_h(\beta _3I_h+\beta _4\kappa D_h)(1-u_4)}{N_h^2},\\ \lambda _{3}^{'}=\theta \lambda _{3}+(\lambda _{1}-\lambda _{2})\frac{S_f\beta _1(1-u_1)}{N_f},\\ \lambda _{4}^{'}=d_h\lambda _4+(\lambda _4-\lambda _5)u_5+(\lambda _6-\lambda _4)\frac{\beta _2 S_h I_h (1-u_3)}{N_h^2}+(\lambda _4-\lambda _6)\frac{\beta _2I_h(1-u_3)}{N_h}\\ +(\lambda _6-\lambda _4)\frac{S_h(\beta _3I_h+\beta _4 \kappa D_h)}{N_h^2}+(\lambda _4-\lambda _6)\frac{(\beta _3I_h+\beta _4 \kappa D_h)(1-u_4)}{N_h},\\ \lambda _{5}^{'}=-A_1+\lambda _5 d_h+(\lambda _5-\lambda _4)\zeta +(\lambda _6-\lambda _4)\frac{\beta _2 S_hI_h(1-u_3)}{N_h^2} +(\lambda _6-\lambda _4)\frac{\beta _2S_hI_h(I_h\beta _3+\kappa d_h\beta _4)(1-u_4)}{N_h^2},\\ \lambda _{6}^{'}=-A_3+(\lambda _6-\lambda _7)u_6+\alpha _1(\lambda _6-\lambda _8)+(\lambda _6-\lambda _9)d_1+\lambda _6d_h+(\lambda _6-\lambda _4)\frac{\beta _2S_hI_h(1-u_3)}{N_h^2}\\ +(\lambda _4-\lambda _6)\frac{S_h\beta _2(1-u_3)}{N_h}+(\lambda _4-\lambda _6)\frac{S_h\beta _3(1-u_4))}{N_h}+(\lambda _6-\lambda _4)\frac{S_h(\beta _3 I_h+\beta _4 \kappa D_h )(1-u_4)}{N_h^2},\\ \dot{\lambda _{7}}=-A_2+d_h\lambda _7+\alpha _2(\lambda _7-\lambda _8)+(\lambda _6-\lambda _4)\frac{\beta _2 S_hI_h(1-u_3)}{N_h^2}+(\lambda _6-\lambda _4)\frac{S_h(\beta _3I_h+\beta _4\kappa D_h)(1-u_4)}{N_h^2},\\ \lambda _{8}^{'}=d_h\lambda _8+(\lambda _8-\lambda _4)\gamma +(\lambda _6-\lambda _4)\frac{\beta _2S_hI_h(1-u_3)}{N_h^2}+(\lambda _6-\lambda _4)\frac{S_h(\beta _3I_h+\beta _4\kappa D_h)(1-u_4)}{N_h^2},\\ \lambda _{9}^{'}=\nu \lambda _9+(\lambda _4-\lambda _6)\frac{\beta _4\kappa S_h(1-u_4)}{N_h},\\ \end{array}\right. } \end{aligned}$$
(46)

with boundary conditions or transversality conditions

$$\begin{aligned} \lambda _{i}(T)=0,i=1,{{\dots }},9. \end{aligned}$$

Moreover, the control measures \(u_{1}^{*}\), \(u_{2}^{*}\),\(u_{3}^{*}\), \(u_{4}^{*}\),\(u_{5}^{*}\) and \(u_{6}^{*}\) are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1}^{*}=\text {max }\{\text {min}(\frac{\beta _{1}S_{f}V(\lambda _{3}-\lambda _{2})}{N_{f}a_{1}},1),0\},\\ u_{2}^{*}=\text {max }\{\text {min}(\frac{\lambda _{3}I_{f}}{a_{2}},1),0\},\\ u_{3}^{*}=\text {max }\{\text {min}(\frac{(\lambda _{6}-\lambda _{4})\beta _{2}I_{h}S_{h}}{N_{h}a_{3}},1),0\},\\ u_{4}^{*}=\text {max }\{\text {min}(\frac{(\lambda _{6}-\lambda _{4})(\beta _{3}I_{h}+\beta _{4}\kappa D_{h})S_{h}}{N_{h}a_{4}},1),0\},\\ u_{5}^{*}=\text {max }\{\text {min}(\frac{(\lambda _{4}-\lambda _{5})S_{h}}{a_{5}},1),0\},\\ u_{6}^{*}=\text {max }\{\text {min}(\frac{(\lambda _{6}-\lambda _{7})I_{h}}{a_{6}},1),0\}. \end{array}\right. } \end{aligned}$$
(47)

Proof

In order to obtain the transversality and adjoint system conditions with the correct boundary values, we utilize the Hamiltonian function \(\mathbb {H}\), as shown in Eq. (31). By employing Pontryagin’s maximum principle, we can derive the adjoint equations in a methodical and effective way.

$$\begin{aligned} \frac{d\lambda _{1}(t)}{dt}=-\frac{\partial {\mathbb {H}}}{\partial S_f}, \frac{d\lambda _{2}(t)}{dt}=-\frac{\partial {\mathbb {H}}}{\partial I_f}, \cdots , \frac{d\lambda _{8}(t)}{dt}=-\frac{\partial {\mathbb {H}}}{\partial D_h}, \end{aligned}$$

subject to boundary time conditions (i.e. final) \(\lambda _{i}(T)=0\) for \(i=1,2,\ldots ,9\). In order to achieve the desired problem (47), we utilize the following equations:

$$\begin{aligned} \frac{\partial {\mathbb {H}}}{\partial u_{i}}=0, ~~i=1,\cdots ,6. \end{aligned}$$

By utilizing the property of the control space U being in the interior of the control set, we obtain the desired result. \(\square\)

Simulation and discussion

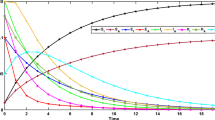
In order to examine the effectiveness of the aforementioned control measures, we conducted a detailed numerical analysis of the NiV epidemic models with variable and constant controls given (26) and (11) respectively. Utilizing the backward fourth-order Runge-Kutta method, the model was numerically solved. The parameter’s values used in simulation are mentioned in Table 2. The balance constants and weights were adjusted to \(A_1=01,~ A_2=A_3=10, ~ a_1=a_2=15,~ a_3=10,~ a_4=15, ~a_5=10\) and \(a_6=50\). The control profile for this scenario is represented by Fig. j in all figures. The red solid plots indicate the dynamics without control, while the black dashed trajectories depict the dynamics with optimal control. Each and every section of graphs have nine classes as: (a) Virus class (b) susceptible flying foxes (c) infected flying foxes (d) susceptible human (e) vaccinated human (f) infected human (g) treated human (h) recovered human (i) deceased human and (j) all controls.

Applying all controls simultaneously, i.e., \(u_i \ne 0,\) where, \(i=1,2,3,4,5,6\)

In order to analyze the effectiveness of optimal control measures in reducing infections in the NiV control model, we conducted simulations that included all suggested control interventions. The simulation demonstrated a notable decrease in the virus and the number of infected individuals among flying foxes, as well as among the susceptible, infected, recovered, and deceased human populations when all control measures were implemented. Conversely, the population of susceptible flying foxes, vaccinated humans, and treated human groups increased with the implementation of optimal controls. For a visual representation of the simulation dynamics, see Fig. 4. It is worth mentioning here that with the application of optimal controls, most of the population in the susceptible class are either vaccinated or protected from the virus (with other non-pharmaceutical measures) as shown in Fig. 4d,e,g, subsequently there are fewer people at risk of infection (see Fig. 4f). This reduction in risk results in fewer infection cases and, consequently, a decrease in the number of recovery cases (see Fig. 4h). The same scenario is observed in all subsequent strategies. This type of behavior can also be found in previous studies, such as the one described in46.

Figure 4
figure 4

Usage of all control interventions.

Full size image

Second strategy: \(u_1 = 0,\) and \(u_i \ne 0,\) where, \(i=2,3,4,5,6\)

In the second strategy, we simulate the NiV model by activating all control interventions simultaneously except \(u_1\) to investigate their combined impact on the disease dynamics. The graphical representation of this scenario is illustrated in Fig. 5, which shows the dynamics of both human and flying fox populations. According to the system (26) with control measures, there was a decrease in the virus and the susceptible and infected populations of flying foxes. Similarly, there was a significant decrease in the susceptible, infected, recovered, and deceased human populations compared to the system (11) without control measures. In contrast, the number of vaccinated and treated individuals showed a significant increase. Figure 5j displays the control profile for this scenario. The graphical findings of this strategy, both with and without control, revealed more noteworthy outcomes for the human population. Thus, control interventions can be effectively used to reduce infection.

Figure 5
figure 5

Usage of all controls except \(u_1\).

Full size image

Third strategy: \(u_2 = 0,\) and \(u_i \ne 0,\) where, \(i=1,3,4,5,6\)

In the third strategy, we simulate the NiV model by activating all control interventions except \(u_2\) simultaneously. This allows us to examine how these interventions work together to affect the disease dynamics. Figure 6 provides a graphical interpretation of this scenario, showing the dynamics of the human and flying fox populations. The results from system (26) with control measures show a decrease in the infected population of flying foxes, but an increase in susceptible flying foxes. Comparing the susceptible, recovered, infectious and deceased human individuals to the system (11) without control measures, a significant drop was observed. However, there was a notable increase in the number of people who received treatment and vaccinations. Figure 6j displays the control profile corresponding to this case. When comparing the results with and without control, it is evident that the control intervention has a more significant impact on the human population in this strategy. Therefore, control interventions can be used to effectively minimize the infection.

Figure 6
figure 6

Impact of using all controls except \(u_2\).

Full size image

Fourth strategy: \(u_3 = 0,\) and \(u_i \ne 0,\) where, \(i=1,2,4,5,6\)

In the fourth strategy, we examine the effects of simultaneously activating all control interventions except \(u_3\) on the dynamics of the NiV model. This helps us understand the combined impact of control measures on the disease dynamics. Figure 7 provides a graphical illustration of this scenario, showing the dynamics of the flying fox and human populations. The results obtained from system (26) with control measures indicate a decrease in the infected population of flying foxes, but an increase in the susceptible flying foxes. Additionally, the population density in susceptible, recovered, infectious and deceased human show a significant decrease compared to the uncontrolled system (11). On the other hand, the density of vaccinated and treated classes observe a substantial increase. The corresponding control profile is depicted in Fig. 7j. The simulation in both cases reveal more significant findings for the human population, indicating that control methods can be effectively employed to reduce the infection.

Figure 7
figure 7

Impact of using all controls except \(u_3\).

Full size image

Fifth strategy: \(u_4 = 0,\) and \(u_i \ne 0,\) where, \(i=1,2,3,5,6\)

In the fifth strategy, we examine the NiV model by activating all control interventions except \(u_4\) simultaneously to observe their effects on disease dynamics. Figure 8 provides a graphical interpretation of this scenario, illustrating the interactions between human and flying fox populations. The results from system (26) with control measures indicate that the virus and the infected population of flying foxes decreased, while the susceptible flying fox population increased. Additionally, the number of susceptible, infected, recovered, and deceased humans notably declined compared to the without variable controls. Conversely, the density of individuals who have received vaccinations and treatments significantly increased. Figure 8j illustrates the profile of all controls corresponding to this scenario. The simulation in both cases show more significant outcomes for the human population in this strategy, indicating that this control interventions can effectively minimize the infection.

Figure 8
figure 8

Impact of using all controls except \(u_4\).

Full size image

Sixth strategy: \(u_5 = 0,\) and \(u_i \ne 0,\) where, \(i=1,2,3,4,6\)

As part of strategy 6, a simulation was conducted on the NiV model by activating all control interventions except for \(u_5\) simultaneously. This was done to observe the collective impacts on the disease dynamics. Figure 9 provides a graphical interpretation of this scenario, outlining the interactions between flying fox and human populations. The control results derived from system (26) indicate a decrease in the virus and the population of infected flying foxes, while the susceptible flying fox population increased. Similarly, in humans, the susceptible, infected, recovered, and deceased populations all saw a significant decrease compared to (11) results without control. Interestingly, the treated class dramatically enhanced, but there was no change in the number of vaccinated individuals. The control profile for this particular instance can be found in Fig. 9j. The simulation with control intervention depicts a reasonable impact on the human population in this strategy, indicating that control measures can effectively minimize the spread of the infection.

Figure 9
figure 9

Impact of using all controls except \(u_5\).

Full size image

Seventh strategy: \(u_6 = 0,\) and \(u_i \ne 0,\) where, \(i=2,3,4,5\)

In the seventh strategy, an analysis was conducted to simulate the NiV model and examine the combined effects of all control interventions except \(u_6\) on the disease dynamics. The simulation results, illustrated in Fig. 10, showed that the infected population of flying foxes decreased, while the susceptible flying fox population increased. In humans, the susceptible, infected, recovered, and deceased populations showed a significant decrease compared to (11) results without control. Moreover, the vaccinated individuals density increased but there was no change observed in the treated individuals. The analysis of both cases i.e., with constant and time-varying strategies demonstrated a higher degree of significance in the human population under the variable strategy. These findings suggest that variable control interventions can be effectively employed to mitigate infection rates and reduce the spread of the disease.

Figure 10
figure 10

Impact of using all controls except \(u_6\).

Full size image

To get a better grasp of the entire process, refer to the following table 3.

Table 3 Description of the suggested strategies.
Full size table

Conclusion

The aim of this study is to present a mathematical model that captures the dynamics of NiV. We developed a mathematical model that considers multiple transmission modes of the virus and combines the impact of treatment and vaccination. The model we formulated includes both human-to-human and food-borne transmissions. We presented a detailed analysis of the model and examined potential problem equilibria based on the reproduction number. It was observed that the model has three equilibrium states: disease-free, infected flying fox-free, and endemic steady state. The model was successfully applied to the reported outbreaks in Bangladesh during 2001-2015, and the parameters were estimated from clinical data. A normalized sensitivity analysis was conducted to identify the most influential parameters in the model. The analysis indicated that increasing treatment strategies, reducing effective contact rates between susceptible and infected populations, and enhancing vaccine efficacy are critical for disease eradication. Further, by incorporating six control variables, a control model was constructed based on the sensitivity analysis. We conducted extensive simulations by considering seven different strategies. Under the optimal control strategy, the simulation demonstrated more significant results in the human population as the number of infected individuals diminished. These findings suggest that time-varying control interventions can effectively mitigate infection rates and limit the spread of the disease. In future studies, we plan to extend the proposed model using a novel fractional and fractal-fractional modeling approaches with perfect and imperfect vaccination.