Introduction

In the field of materials science, researchers are constantly striving to discover superconductors with improved transition temperatures. Investigating the superconducting characteristics of existing materials is essential for making progress in this area. The Bardeen–Cooper–Schrieffer (BCS) theory1 proposes that materials with lower mass could potentially exhibit higher transition temperatures, which may be associated with a higher frequency or Debye temperature. Nonetheless, this theory is mostly applicable to compounds that contain a significant amount of hydrogen2,3,4. Another intriguing group of materials that deserves attention is the MAX phase compounds. These compounds, which have emerged in the last two decades5,6,7, have the chemical formula \(\hbox {M}_{n+1}\hbox {AX}_{{n}}\) (where n = 1, 2, or 3), with “M”, “A”, “X” representing an early transition metal, an element from groups 13–16 in the periodic table, and carbon or nitrogen, respectively8. Currently, more than 150 MAX phase compounds with various compositions have been successfully synthesized9,10,11,12,13,14,15,16,17,18,19. These materials possess a combination of ceramic and metal properties, exhibiting fascinating characteristics such as high thermal and electrical conductivity as well as high mechanical stabilities20,21. As a result, they can be classified as multifunctional materials. These material have significant application in electrical contacts, sensors, protective coating, and high-temperature structural materials. The distinctive properties of MAX phases originate from their lamellar structure, which is composed of metallic/covalent bonds and relatively weak bonds between the M and A layers. The layered configuration is formed by the \(\hbox {M}_{{6}}\)X blocks and A layers, with the space group P\(6_{3}\)/mmc. This space group resemble to that of the \(\hbox {MgB}_{{2}}\) superconductor with high \(T_{c}\) of 39 K22. So, it might be interesting to explore various \(\hbox {M}_{{2}}\)AX compositions, to uncover their superconducting behavior.

It is worth noting that only 10 MAX phases have been identified as superconductors, with a maximum \(T_{c}\) of 10 K, up until now23, namely \(\hbox {Ti}_{{2}}\)InC24, \(\hbox {Ti}_{{2}}\)InN25 , \(\hbox {Ti}_{{2}}\)GeC26, \(\hbox {Lu}_{{2}}\)SnC27, \(\hbox {Nb}_{{2}}\)SC28, \(\hbox {Nb}_{{2}}\)SnC29, \(\hbox {Nb}_{{2}}\)AsC30, \(\hbox {Nb}_{{2}}\)InC31,\(\hbox {Nb}_{{2}}\)GeC32 and \(\hbox {Mo}_{{2}}\)GaC33 whit \(\hbox {T}_{{c}}\sim\) 3.1 K−10 K. All of these materials become superconductor under ambient conditions. However, there are some ambiguities in these experimental data. For example, in the case of \(\hbox {Nb}_{{2}}\)GeC the observed superconductivity may be due to the presence of impurities phase such as NbC32. To resolve such ambiguities in superconducting properties of \(\hbox {Nb}_{{2}}\)AC compounds the ab initio calculations are necessary. On the other hand, despite the growing interest, a comprehensive understanding of the underlying mechanisms of superconductivity for these materials remains elusive. In addition, increasing the transition temperature of superconducting compounds has always been one of the important challenges facing researchers. Based on researches findings, techniques like electron/hole doping, hydrostatic pressure application, and uniaxial and biaxial tension are commonly recommended for this objective. Numerous theoretical and experimental outcomes have consistently shown an enhancement in superconductivity transition temperature across various compounds through the utilization of these methods34. For instance, studies have demonstrated that the transition temperature of \(\hbox {MgB}_{{2}}\) can be heightened by applying pressure and plane strain35. Additionally, graphene has been made superconductive through carrier doping and tensile strain36. An illustration of this is aluminum-deposited graphene \(\hbox {AlC}_{{8}}\), which exhibits superconducting properties with a \(\hbox {T}_{{c}}\) of 22.2 K when hole doping and biaxial tensile strain are utilized37. Researchers have also investigated the impact of pressure on the structural characteristics of MAX phases. Hence, it would be fascinating to investigate the effects of pressure on the superconducting behavior of MAX phases. By increasing the superconducting transition temperature of MAX phase the application of these multifunctional materials could be extend to low temperature physics. Such advancement is significant given the growing variety of MAX phases, including various subtypes such as typical MAX phases38, o-MAX phases39, i-MAX phases40, and superlattice MAX phases41.

In this study, we have conducted a thorough examination of the electronic structure and superconductivity transition temperature of \(\hbox {Nb}_{{2}}\)SC and \(\hbox {Nb}_{{2}}\)AsC compounds using density functional theory. We investigate the electronic band structure, lattice dynamics, and phonon-mediated electron pairing mechanisms. By combining theoretical calculations with experimental data, we reveal the critical factors governing superconductivity in these layered materials. Our work provides insights into the vibrational modes responsible for electron–phonon coupling. Our findings indicate that the transition temperature of these compounds can be significantly altered by applying uniform pressure or uniaxial tensile strain. It has been proven that subjecting pressure up to several tens of gigapascals can lead to a twofold increase in the \(\hbox {T}_{{c}}\) of specific MAX phases.

Methods

All structural optimizations and electronic structure calculations were performed within the framework of density functional theory (DFT)42 implemented in the Quantum-ESPRESSO (QE)43,44 software package. A parametrized Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) was used to account for the exchange-correlation energy45,46. An ultrasoft pseudopotential with a plane wave cutoff energy of 60 Ry and a charge density of 600 Ry was used to simulate interactions between electrons and ionic nuclei.The electronic configurations considered for the valence electrons were Nb:5\(\hbox {s}^{2}\) 4\(\hbox {d}^{3}\), As:4\(\hbox {s}^{2}\) 4\(\hbox {p}^{3}\) 3\(\hbox {d}^{10}\) , S:3\(\hbox {s}^{2}\) 3\(\hbox {p}^{4}\) , C:2\(\hbox {s}^{2}\), 2\(\hbox {p}^{2}\). The BFGS algorithm47 is applied for the optimization of lattice constants and atomic positions, with energy and force convergence criteria set at \(10^{-8}\) Ry and \(10^{-7}\) Ry/a.u, respectively. Following this, Density Functional Perturbation Theory (DFPT)48 is utilized to calculate the dynamics matrix and electron–phonon coupling (EPC) parameter within the linear response approximation. SCF calculations are carried out using an 8 × 8 × 8 k-point mesh, while a denser 24 × 24 × 24 k-point grid is employed for accurate evaluation of the electron–phonon interaction matrix. Additionally, a 4 × 4 × 4 q-point grid is used for standard phonon calculations. Fermi velocities of compounds were calculated using the electronic band structures by \(v_{F}=\hbar ^{-1}\nabla _{k}\varepsilon _{k}|_{\varepsilon =E_{F}}\).

The structures subjected to biaxial tensile and compressive strains were created by adjusting lattice parameters and reoptimizing configurations. The strains were determined using the formula \(\varepsilon =(\frac{a-a_{0}}{a_{0}})\times 100\), where “a” denotes the strained lattice constant and “\(a_{0}\)” denotes the unstrained lattice constant. The Murnaghan equation of state49 was utilized to compute the lattice constants of a and c.

The critical temperatures for superconductivity and electron–phonon coupling are determined through the use of the Eliashberg spectral function and McMillan equation50,51,52. The spectral function evaluates how efficiently phonons with energy \(\hbar \omega\) scatter electrons across different regions of the Fermi surface. This function is calculated by summing up the contributions to the coupling from individual phonon modes, i.e.

$$\begin{aligned} \alpha ^{2}F(\omega )=\frac{1}{2\pi N(E_{F})}\sum _{qv}\delta (\omega -\omega _{qv}) \frac{\gamma _{qv}}{\hbar \omega } \end{aligned}$$
(1)

Here, N(\(E_{F}\)) represents the density of states at the Fermi level. The phonon frequency \(\omega _{qv}\) is associated with the scattering of an electron from one Bloch state nk to another Bloch state \(nk+q\).

The interaction between electrons and phonons leads to a finite phonon linewidth \(\gamma _{qv}\), which can be calculated using Eq. (2) in the double-delta function approximation.

$$\begin{aligned} \gamma _{qv}=2\pi \omega _{qv}\sum _{i,j}\frac{d^{3}k}{\Omega _{BZ}}|g_{qv(k,i,j)}|^{2}\delta (E_{q,i}-E_{F})\delta (E_{k+q,j}-E_{F}) \end{aligned}$$
(2)

where \(\Omega _{BZ}\) is the volume of the Brillouin zone (BZ), \(E_{q,i}\) and \(E_{k+q,j}\) indicate the Kohn–Sham energy, and \(g_{qv(k,i,j)}\) represents the screened electron–phonon matrix element.The \(\lambda _{qv}\) is the EPC constant for phonon mode qv, which is defined as:

$$\begin{aligned} \lambda _{qv}=\frac{\gamma _{qv}}{\pi \hbar N(E_{F})\omega _{qv}^2} \end{aligned}$$
(3)

The total electron–phonon coupling \(\lambda\) is obtained by averaging the mode-resolved coupling strengths \(\lambda _{qv}\) over the Brillouin-zone as defined below:

$$\begin{aligned} \lambda =\sum _{qv}\lambda _{qv}=2\int _{0}^{\infty }\frac{\alpha ^{2}F(\omega )}{\omega }d\omega \end{aligned}$$
(4)

So, \(\lambda\) is related to twice of the first inverse moment of the Eliashberg spectral function \(\alpha ^{2}\)F\((\omega )\).The transition temperature \(\hbox {T}_{{c}}\) is estimated by the modified McMillan formula51 :

$$\begin{aligned} T_{c}=\frac{\omega _{log}}{1.2} \exp \left[ \frac{-1.04(1+\lambda )}{\lambda -\mu ^{*}(1+0.62\lambda )}\right] , \omega _{log}=\exp (\frac{2}{\lambda }\int \frac{\log \omega }{\omega }\alpha ^{2}F(\omega )d\omega ) \end{aligned}$$
(5)

According to experimental data the Coulomb parameter \(\mu ^{*}\) in Eq. (5) adjusted to 0.1 and 0.16 for \(\hbox {Nb}_{{2}}\)AsC and \(\hbox {Nb}_{{2}}\)SC respectively.

Results

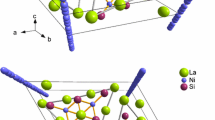
The \(\hbox {Nb}_{{2}}\)AC compounds possess a hexagonal close-packed arrangement, where the Nb, C, and A atoms are organized in the \(\hbox {P6}_{{3}}\)/mmc space group. Figure 1 illustrates a side view of \(\hbox {Nb}_{{2}}\)AC (A: S, As), emphasizing the \(\hbox {Nb}_{{2}}\)C layers separated by A atoms. It is worth highlighting that in certain MAX phases like \(\hbox {Ti}_{{2}}\)AlC, where the M-A bonds are comparatively weaker than the M-C bonds, the A atoms can be removed through chemical exfoliation while the \(\hbox {M}_{{2}}\)C backbone remains intact. This process leads to the creation of innovative 2D \(\hbox {M}_{{2}}\)C multilayer materials. Figures 2 and 3 depict the total densities of states (TDOS) and partial densities of states (PDOS) for the \(\hbox {Nb}_{{2}}\)SC phases and \(\hbox {Nb}_{{2}}\)AsC, respectively. Also, the variations of TDOS by applying pressure presented in Figs. 2c and 3c. Similar to other MAX phases, the \(\hbox {Nb}_{{2}}\)AC phases exhibit metallic properties. The d orbitals of the transition metal (Nb) make significant contributions to the states near the Fermi energy, while the contributions from S/As and C atomic orbitals are relatively minor in this region. Figures 2a and 3a showcase the band structures of \(\hbox {Nb}_{{2}}\)SC and \(\hbox {Nb}_{{2}}\)AsC, respectively, presented along the high symmetrical directions of the Brillouin zone within the energy range of - 3 to + 3 eV. In \(\hbox {Nb}_{{2}}\)SC, there are five bands intersecting the Fermi level, whereas in \(\hbox {Nb}_{{2}}\)AsC, there are three bands. These band characteristics ensure the metallic conductivity of these compounds. In the lower energy range, significant hybridization occurs between the d orbitals of the Nb atom and the p states of A atoms (S, As), resulting in robust directional covalent Nb-A bonding. The Fermi energy in these compounds is located in a local minimum, distinguishing between bonding and non-bonding states, implying the structural stability of these systems.

Figure 1
figure 1

The hexagonal crystal structure of \(\hbox {Nb}_{{2}}\) AC (A: S, As).

Full size image

The application of hydrostatic pressure, tensile/strain (biaxial or uniaxial) are well established approaches to modifying the structural or electronic characteristics of materials. In our research, we have explored how applying pressure up to 50 GPa and various strains can impact the structural and electronic properties of \(\hbox {Nb}_{{2}}\)AC compounds. Our results indicate that while there are changes in lattice parameters under pressure or strain, the original structure symmetry remains unchanged at \(\hbox {P6}_{{3}}\)/mmc. The details of lattice parameters can be found in Table 1.

When pressure or strain is exerted, the \(d_{\textit{x}z}\) and \(d_{\textit{z}y}\) bands of Nb atoms in \(\hbox {Nb}_{{2}}\)AC exhibit an increase in their influence on the Fermi level. This enhancement in the density states at the Fermi level, attributed to these orbitals, suggests a greater possible involvement of electrons from these orbitals in Copper pair formation. As a result, this may result in changes in the superconducting characteristics of the material.

It is intriguing to examine the impact of pressure on the role of electrons near the Fermi surface in the formation of the superconducting state. By analyzing both bonding and non-bonding states, we can gain valuable insights. In the supplementary information, Figs. 3 and 4 shows the crystal orbital overlap population (COOP) for \(\hbox {Nb}_{{2}}\)SC and \(\hbox {Nb}_{{2}}\)AsC before and after applying pressure. Interestingly, the application of pressure to these compounds results in a decrease in energy for the bonding states, leading to stronger bonds. These results are consistent with the shift of TDOS in Figs. 2 and 3 to lower energies. However, the non-bonding states show minimal changes near the Fermi energy in both materials. Notably, the decrease in non-bonding states will be more pronounced for \(\hbox {Nb}_{{2}}\)AsC.

Figure 2
figure 2

Band structure (a) Total and partial density of states (b), Compartion of total density of state before and after applying pressure (c) (Fermi energy is set at zero) and 2D Fermi surface without pressure (d) and under 50 GPa pressure (e) for the \(\hbox {Nb}_{{2}}\)SC compound.

Full size image
Figure 3
figure 3

Band structure (a) Total and partial density of states (b), Compartion of total density of state before and after applying pressure (c) (Fermi energy is set at zero) and 2D Fermi surface without pressure (d) and under 50 GPa pressure (e) for the \(\hbox {Nb}_{{2}}\)AsC compound.

Full size image

The Fermi surfaces (Fig. 2d,e and 3d,e) are color-coded to represent the Fermi velocity \(v_{F}\), which signifies the gradients of the bands intersecting the Fermi energy. Upon analyzing the band structures, it is noted that in \(\hbox {Nb}_{{2}}\)SC, five bands cross \(\hbox {E}_{{F}}\) (Fig. 2d), three bands creating three hexagonal-shape electron pocket centered at \(\Gamma\) and two other bands creating tubular-shaped hole pockets centered at M on the Fermi surface. The \(\Gamma\)-centered pocket displays lower Fermi velocities, while the pockets around the K points exhibit the highest Fermi velocities. Under pressure, the Fermi surface of \(\hbox {Nb}_{{2}}\)SC (Fig. 2e) exhibits six sheets, five resemblance to the observed bands at zero pressure, and the shifted band is in \(\Gamma\)-K direction whit electron-like characterization. The rise in conductivity resulting from the non-spherical form of the plate could potentially contribute to a higher transition temperature53.

Furthermore, the Fermi surface of \(\hbox {Nb}_{{2}}\)AsC exhibits a unique characteristic with the presence of four bands, Fig. 3d. Specifically, two bands intersect the Fermi level in the \(\Gamma\)-A direction, while the other two bands intersect in the \(\Gamma\)-K direction. Under normal conditions, electrons in \(\hbox {Nb}_{{2}}\)AsC are primarily localized near the \(\Gamma\) point. However, the introduction of pressure enhances the velocity of these electrons. Figure 3d illustrates a 2D-projected Fermi surface of the \(\hbox {Nb}_{{2}}\)AsC compound, consisting of two bands primarily composed of Nb \(d_{\textit{x}y}\) and \(d_{\textit{z}y}\) orbitals. These bands intersect the Fermi level along the K–M and H–L directions, forming M-centered arc-like hole pockets at the edges of the Brillouin zone and small oval-shaped electron pockets near the center. Under 50 GPa pressure, an additional star-like Fermi surface with lower Fermi velocity emerges around the \(\Gamma\) point, Fig. 3e. The average Fermi velocity of this compound increases with pressure, similar to \(\hbox {Nb}_{{2}}\)SC, as indicated in Table 2. The data shows that electrons at the Fermi surface travel with a velocity \(v_{F}\) ranging from 0.1\(\times 10^{6}\) m/s to 0.5\(\times 10^{6}\) m/s.

Table 1 Lattice parameters of the hexagonal \(\hbox {Nb}_{{2}}\)AC (A: S, As), density of states at Fermi level \(N(E_{F})\), average velocity changes at the Fermi level \(v_{F}\) and finally the transition temperature for each pressure or tension \(\hbox {T}_{{c}}\).
Full size table

Phonons and electron–phonon interaction

Figure 4 illustrates the phonon dispersion curves as well as the total and partial phonon density of states of \(\hbox {Nb}_{{2}}\)AC. The phonon spectrum shows a wide frequency range that goes beyond 800 \(\hbox {cm}^{-1}\). It is worth mentioning that the absence of imaginary phonon frequencies indicates that the compounds are dynamically stable under normal ambient conditions. The compounds are composed of eight atoms in their primitive cell, which gives rise to a total of 24 phonon branches. These branches include three acoustic branches and 21 optical branches. Additionally, the \(\hbox {Nb}_{{2}}\)AC structures exhibit three acoustic branches, consisting mainly of one out-of-plane mode and two in-plane modes. By examining the phonon density of states (PhDOS) projected on Nb, A, and C atoms, it is evident that in these structures, the lower frequencies are mainly influenced by vibrations of Nb and A atoms (Fig. 4), whereas the highest optical branch consistently arises from the vibrations of C atoms. The difference stems from the diverse mass of the atoms found in the unit cell. It is established that the phonon vibration frequency’s magnitude is inversely related to the square root of the atomic mass. Hence, the lighter the atom, the higher the \(\omega _{qv}\). It seems that, based on Eq. 5, the impact of higher frequency phonon modes \(\omega _{qv}\) will diminish in the \(\omega _{log}\). Consequently, the lower frequency modes dictate the value of \(\hbox {T}_{{c}}\). Furthermore, the resemblance between the Eliasberg function and the phonon density of states (Fig. 4) suggests that the ratio \(\frac{\gamma _{qv}}{\omega _{qv}}\) is nearly identical for most q-modes. This finding provides support for the assumption that low frequencies dominate. In fact, based on the definition of mode-resolved coupling strengths \(\lambda _{qv}\) [Eq. (3)], low frequencies play a significant role in the overall electron–phonon coupling \(\lambda\), given the constant ratio of \(\frac{\gamma _{qv}}{\omega _{qv}}\). The electron–phonon coupling parameter remains relatively constant for \(\omega _{qv}\) > 10 THz, as depicted in Fig 4e and f. According to these data, the calculated values of \(\lambda\) [Eq. (4)] for \(\hbox {Nb}_{{2}}\)AC are 0.744 and 0.441, respectively. In both cases, approximately 93% of the total \(\lambda\) is attributed to low-frequency contributions, primarily originating from the vibrations of Nb and A atoms. We analyze the zone-center phonon modes of \(\hbox {Nb}_{{2}}\)SC and \(\hbox {Nb}_{{2}}\)AsC, which are classified based on the irreducible representations of the point group \(\hbox {D}_{{6h}}\)(6/mmm). According to group theory, the symmetries of the zone-center optical phonon modes are described as follows:

$$\begin{aligned} \Gamma =2E_{1u}+2E_{2u}+2A_{2u}+2B_{2u}+2B_{1g}+2E_{2g}+E_{1g}+A_{1g} \end{aligned}$$

The B and A modes, which are doubly degenerate, are associated with the movement of specific atoms along the \(\textit{c}\)-axis, whereas the E modes pertain to the vibrations of relevant atoms within the a–b plane. The primary one-dimensional \(A_{1g}\) and \(E_{1g}\) modes, crucial for electron–phonon coupling, correspond to the vibrations of pertinent atoms along the c-axis and a-b plane, respectively. While other modes have minimal impact, the \(E_{2g}\) mode in \(\hbox {Nb}_{{2}}\)AsC also plays a significant role. In \(\hbox {Nb}_{{2}}\)SC, the impact of the \(E_{2g}\) mode on electron–phonon interaction is initially insignificant under zero pressure conditions. However, as pressure is applied, the interaction in this mode intensifies. In the lowest \(E_{g}\) mode, specifically \(E_{1g}\), half of the Nb and S atoms exhibit oscillations in opposite directions along the a-b plane. The \(A_{1g}\) phonon mode corresponds to the vibration of Nb atoms, while the other atoms remain stationary. It is worth noting that the atomic displacement patterns of the \(E_{1g}\), \(E_{2g}\), and \(A_{1g}\) phonon modes in \(\hbox {Nb}_{{2}}\)AsC closely resemble those in \(\hbox {Nb}_{{2}}\)SC. The vibration modes of \(\hbox {Nb}_{{2}}\)SC or \(\hbox {Nb}_{{2}}\)AsC compounds, which have significant electron–phonon coupling (EPC) and play a major role in EPC, are illustrated in Fig. 5. Table 2 displays the coupling frequencies between various modes. The phonon dispersion, weighted by the magnitude of EPC \(\lambda _{qv}\), represented in Fig.  4b, reveals that the predominant mode in these materials is \(A_{1g}\). Notably, an increase in pressure results in a higher frequency for the \(A_{1g}\) mode in these compounds. When considering the \(\hbox {Nb}_{{2}}\)AsC compound, the \(A_{1g}\) vibration mode is positioned adjacent to the \(B_{1g}\) mode, which oscillate in the opposite directions. By applying pressure or uniaxial tensile to decrease the lattice length in the c-direction, the \(A_{1g}\) and \(B_{1g}\) modes will be separated. Consequently, this action will cause an increase in the frequency of the \(A_{1g}\) mode, ultimately preventing a rise in the electron–phonon coupling parameters (\(\lambda\)) as outlined in Eq. (4). On the other hand, if the c-axis is elongated due to uniaxial compression or tension, it will prevent an increase in its frequency.

Table 2 The calculated zone-center optical phonon frequencies (in \(\hbox {cm}^{-1}\)) and their electron–phonon coupling parameters (\(\lambda\)) for hexagonal \(\hbox {Nb}_{{2}}\)AC.
Full size table

The reason behind the distinction between the \(A_{1g}\) and \(B_{1g}\) vibration modes caused by uniaxial compression or tensile is that only Nb atoms vibrate in the \(A_{1g}\) mode, while both Nb and As atoms vibrate in the \(B_{1g}\) mode. The increase in frequency of the \(B_{1g}\) mode, resulting from the vibration of the heavier As atoms, will be considerably smaller, leading to the separation of these two vibrational modes. Enhancing the coupling of mode \(A_{1g}\) for \(\hbox {Nb}_{{2}}\)AsC poses a significant challenge, whereas increasing the frequency and ultimately the coupling of modes \(E_{1g}\) and \(E_{2g}\) can be achieved through the application of uniaxial tensile and compression.

The application of 50 GPa pressure notably changes the dominant vibration from S atoms to Nb atoms in the \(A_{1g}\) mode of \(\hbox {Nb}_{{2}}\)SC. Due to the heavier nature of Nb atoms compared to S atoms, their frequency increase is relatively restricted. However, in the case of \(\hbox {Nb}_{{2}}\)AsC, still the dominant vibration mode will be associated with As atoms even under pressure, leading to a significant frequency increase. Equation (4) illustrates the inverse relationship between frequency and \(\lambda\), suggesting that temperature can either rise or fall. In order to evaluate the impact of various contributions on \(\hbox {T}_{{c}}\), Eq. (3) can be employed to analyze the alterations in \(\lambda _{qv}\):

$$\begin{aligned} \frac{\lambda _{2}}{\lambda _{1}}=\frac{\gamma _{2}}{\gamma _{1}}\times \left(\frac{\omega _{1}}{\omega _{2}}\right)^{2}\times \frac{N{(E_{F})_{1}}}{N{(E_{F})_{2}}} \end{aligned}$$
(6)

This formula allows us to evaluate the importance of each variable with respect to \(\lambda\), track any changes, and compare these variables across under different condition. \(\hbox {Nb}_{{2}}\)SC has experienced an increase in \(\lambda\) due to the contribution of the density of states at the Fermi level and the phonon linewidth \(\gamma\). The only factor that has reduced \(\lambda\) is the frequency \(\omega\), which has undergone minimal changes. On the other hand, in the case of \(\hbox {Nb}_{{2}}\)AsC, applying pressure has resulted in a significant increase in frequency and a decrease in \(\lambda\). This ultimately leads to a reduction in the transition temperature. Eliashberg’s \(\alpha ^{2}\)F\((\omega )\) plot illustrates this scenario.

In our study, we conducted a further analysis on the impact of uniaxial compression on the superconductivity temperature of \(\hbox {Nb}_{{2}}\)AC compounds. Specifically, we investigated the effects of 2% and 4% uniaxial tensile and compression in the a or b direction for both compounds. Our findings, as depicted in Figs. 1 and 2 of the Supplementary information, clearly indicate that uniaxial tensile leads to an increase in \(\lambda\), accompanied by a noticeable decrease in frequency for \(\hbox {Nb}_{{2}}\)SC. This increase in \(\lambda\) can be attributed to the strong influence of low-frequency modes on \(\lambda\), as explained by Eq. (3). Consequently, the decrease in frequency within this range contributes to the overall increase in \(\lambda\). Conversely, the application of tension also results in an increase in the N(\(\hbox {E}_{F})\) value, which in turn reduces \(\lambda\). However, the rise in \(\lambda\) caused by phonon softening is counteracted by the decreases resulting from the variation of N(\(\hbox {E}_{{F}}\)), leading to an overall increase in the transition temperature. However, it worth noting that while an increase in N(\(\hbox {E}_{{F}}\)) reduces the electron–phonon coupling constant, the higher density of states at the Fermi level could enhance the likelihood of electron pairing and consequently the emergence of superconductivity. As mentioned earlier, the \(A_{1g}\) mode, which is dominant, vibrates in the c direction, making it susceptible to frequency reduction due to transverse tension. Conversely, \(\hbox {Nb}_{{2}}\)AsC displays strong coupling in transverse modes \(E_{1g}\) and \(E_{2g}\), leading to an increase in their frequencies and a subsequent decrease in transition temperature under tensions.

In both compounds, a 2% and 4% uniaxial tensile strain was applied separately in the c, a or b directions. The \(E_{1g}\) and \(E_{2g}\) modes, crucial for electron–phonon coupling in \(\hbox {Nb}_{{2}}\)AsC, primarily vibrate within the a-b plane. Analysis of the optimized parameters in Table 1 shows that stretching the c-axis direction results in a reduction in parameters a and b. This causes the frequency of the main coupling modes to decrease, ultimately leading to an increase in the transition temperature. Conversely, in \(\hbox {Nb}_{{2}}\)SC, where the main coupling modes align predominantly with the c-direction, the tensile strain has minimal effect on the frequency of these modes. As mentioned above, the superconducting transition temperature can be calculated by estimating the Coulomb pseudopotential (\(\mu ^{*}\)), which typically ranges between 0.10 and 0.1653,54. Through fitting the experimental temperature data, we were able to determine the specific value of \(\mu ^{*}\). In the case of the \(\hbox {Nb}_{{2}}\)SC compound, the value was identified as 0.16, whereas for the \(\hbox {Nb}_{{2}}\)AsC compound, it was determined to be 0.1. In the \(\hbox {Nb}_{{2}}\)SC compound, the applied pressure does not have a notable effect on the quantity of N(\(\hbox {E}_{{F}}\)), thus it is justifiable to assume that the value of \(\mu ^{*}\) remains unaltered. However, in the case of \(\hbox {Nb}_{{2}}\)AsC, the value of \(\mu ^{*}\) increases due to the decrease in N(\(\hbox {E}_{{F}}\)). As a result, our calculations determine the upper limit for the transition temperature in this particular scenario, assuming a constant value of \(\lambda\).

It seems that the impact of pressure, tension, and uniaxial compression on the transition temperature of these structures could be substantial. Through the analysis of vibration and frequency of modes with the highest electron–phonon coupling, as well as evaluating the Fermi level in this family of materials, it becomes feasible to identify potential structures that could enhance temperature by different scenarios.

Figure 4
figure 4

(a, b) show phonon dispersion curves, total and partial vibrational density of states for \(\hbox {Nb}_{{2}}\)SC at zero and 50 GPa pressure, respectively. (c, d) provide similar information for \(\hbox {Nb}_{{2}}\)AsC at zero and 50 GPa. (e, f) electron–phonon spectral function \(\alpha ^{2}F(\omega )\) before and after applying pressure for \(\hbox {Nb}_{{2}}\)SC and \(\hbox {Nb}_{{2}}\)As, respectively.

Full size image
Figure 5
figure 5

The vibration modes of \(\hbox {Nb}_{{2}}\)SC or \(\hbox {Nb}_{{2}}\)AsC compound that have a major role in the EPC mechanism. The arrows indicate the atomic vibration directions. The vibration frequencies for each mode are also shown in Table 2.

Full size image

Conclusions

In this study, we have conducted an extensive analysis of \(\hbox {Nb}_{{2}}\)AC MAX phase superconductors by employing first-principles methods. Our investigation focused on examining the effects of hydrostatic pressure, uniaxial tension, and pressure on the superconducting properties of these materials. To assess the potential for superconductivity, we utilized the BCS theory in combination with ab initio calculations of electronic and vibrational characteristics, as well as the electron–phonon interaction. By employing this comprehensive approach, we aimed to gain insights into the superconducting behavior of \(\hbox {Nb}_{{2}}\)AC MAX phase compounds under different external conditions. As revealed by our research, applying pressure up to 50 GPa has been found to have the ability to either double or halve the transition temperature of superconductivity. The behavior of the compounds under pressure varies depending on the direction of vibration of the dominant modes in electron–phonon coupling (EPC). By considering the vibration axis of the predominant modes, the transition temperature can be further enhanced through the application of uniaxial tension and pressure. The temperature of the \(\hbox {Nb}_{{2}}\)SC composition can be increased from 5.89 to 9.63 by subjecting it to a pressure of 50 GPa. However, an alternative method to raise the temperature to 7.86 involves applying uniaxial tension in the a–b direction. On the other hand, in the case of the \(\hbox {Nb}_{{2}}\)AsC composition, the dominant vibrational modes oscillate in the c-direction. Therefore, by applying uniaxial tensile strain in the c-direction, the temperature can be increased from 2.12 to 2.97. This temperature increase is attributed to the \(\hbox {A}_{{1g}}\) electron–phonon coupling mode that according to Table 2, the value of coupling has increased significantly.