Introduction

Intelligent components play a leading role in Micro-/Nano-Electro-Mechanical System (MEMS/NEMS). In general, intelligent components rely on electromechanical coupling effects to perform specific functions, such as piezoelectric effect. However, recently, flexoelectric effect has received a lot of attention. Flexoelectric effect is a kind of higher-order electromechanical coupling effect, which has a great prospect in the field of sensing, actuating, energy harvesting and so on1,2. The advantage of flexoelectric effect is that, on the one hand, it exists in all dielectric materials, which broadens the choice of suitable materials for electromechanical applications, and, on the other hand, it is size-dependent which will be enhanced in the nano scale.

Flexoelectric effect includes its direct effect and inverse effect3. A polarization can be induced by strain gradient in the direct flexoelectric effect, and elastic stresses can also be induced by polarization gradient in the inverse flexoelectric effect. Many experiments have investigated the flexoelectric effect in ceramics4,5,6, polymers7, biological materials8 and semiconductor9. Shu et al. summarized the measurement methods of flexoelectric coefficients1. A non-polarized PVDF curved flexoelectric actuator with high displacement resolution has been designed by Zhang et al.10. Kwon et al.11 fabricated a flexoelectric microphone possessing a wide working frequency range and a high sensitivity simultaneously. By fabricating a silicon-compatible flexoelectric cantilever actuator, Bhaskar et al.12 demonstrated that flexoelectricity is an alternative to lead-free MEMS and NEMS.

For capturing the flexoelectric effect, the continuum theory for flexoelectricity in dielectric has been proposed on the basis of thermodynamics. Tagantsev developed the flexoelectric theory of solid crystalline dielectrics13. Sahin and Dost choose the deformation gradient, the first and second gradients of deformation gradient, the polarization and polarization gradient as independent variables to describe both the direct and converse flexoelectric couplings14. However, the plethora of parameters restricted its applications. Hence, by taking the strain, polarization and their gradients as independent variables, Maranganti et al.15 proposed a modified flexoelectric theory. The variational principle of flexoelectric theory has been developed by Hu and Shen16 and the corresponding governing equations for flexoelectricity were derived. Then the surface effects were introduced and the electric enthalpy variational principle with surface effects was presented17. Furthermore, the flexoelectric theory has been reformulated by Li et al.18 by introducing the strain gradient orthogonal components. In addition, the flexoelectric theories considering rotation gradient effect rather than strain gradient effect have also been presented19,20. Deng et al. developed a nonlinear theoretical framework for flexoelectricity in soft materials21. The generalized form of the bias-strain-concentration equation has been derived by Morozovska et al. for mixed ionic-electronic conductors22. Moreover, Wang et al.3 reviewed the development of flexoelectric theories in solids and an overview of numerical procedures on modeling flexoelectricity has been provided by Zhuang et al.23.

According to the flexoelectric theory, Li et al. analyzed the flexoelectric effects of an isotropic bar in compression, torsion and bending24. Qi et al. presented a curved flexoelectric beam model and analyzed the flexoelectric responses25. Gabr and El Dhaba extended the isotropic beams to anisotropic beams with cubic symmetry and investigated the flexoelectric response in bending26. By introducing surface and thermal effects, Barati has studied the nonlinear behavior of flexoelectric beam in vibration27. The dynamic flexoelectric actuation of a cantilever actuated by the inverse flexoelectric effect has been evaluated by Fan et al.28. Bagheri and Beni studied the forced vibration of viscoelastic/flexoelectric nanobeams29. Baroudi and Najar revealed the effects of geometric nonlinearity on the static and dynamic responses of piezoelectric flexoelectric nanobeams30. Dai et al. analyzed the output performance of flexoelectric beam energy harvester with the consideration of geometric nonlinearity31. The size-dependent dynamic pull-in instability of micro/nanobeams with considering von Kármán hypothesis has been investigated according to the nonlocal strain gradient theory tuned by flexoelectric and piezoelectric effects32.

In addition, the flexoelectric responses of circular plate have been investigated by Li et al.33. Amir et al. presented a dynamic model of nanocomposite sandwich plates resting on Pasternak foundation34. The nonlinear functionally graded sandwich porous core nano-plates model has been proposed by Zeng et al.35. The nonlinear behavior of functionally graded flexoelectric nano-plate has been studied by Ghobadi et al. in thermal environment36. Moreover, the energy harvesting performance of a flexoelectric plate attached to an elastic substrate was also investigated and the optimal inner and outer radii were identified for maximum power output37.

As the representative intelligent components in MEMS/NEMS, flexoelectric circular plate lacks enough attention. As far as we know, the flexoelectricity in nonlinear behaviors of circular plate is still absent. This paper is devoted to investigating the electromechanical coupling behavior of intelligent components of the circular plate type in large deflection. On the basis of the isotropic flexoelectric theory reviewed in the next Section, the flexoelectric model of circular plate in large deflection deformation is presented in “Nonlinear flexoelectric model for circular plate”. Then by applying the differential quadrature method (DQM) to discretize the current model in “Nonlinear bending of flexoelectric circular plate”, the nonlinear static bending properties of a flexoelectric plate in simply supported boundary conditions are investigated. “Nonlinear free vibration of axisymmetric flexoelectric circular plate” studied the nonlinear free vibration properties of a flexoelectric plate by combining the Galerkin method and Lindstedt–Poincaré Method. Finally, “Conclusion” obtained the conclusion. It is hoped that this paper will be helpful to promote the application of flexoelectric intelligent components of the circular plate type.

Review of the isotropic flexoelectric theory

In flexoelectric theory, the internal energy density U can be expressed as a function of independent variables which includes strain gradient ηijk and polarization gradient Qij except to the traditional strain εij and polarization Pi, written as U = U(εij, Pi, ηijk, Qij)18. The strain εij, the strain gradient ηijk and the polarization gradient Qij are defined, respectively, as

$$\varepsilon_{ij} = \frac{1}{2}(u_{i,j} + u_{j,i} ),\,\,\eta_{ijk} = \varepsilon_{jk,i} ,\,\,Q_{ij} = P_{i,j} ,$$
(1)

where a comma means differentiation with respect to coordinates and ui represents displacement component. For isotropic dielectrics, the general expression of flexoelectric internal density involves five higher-order material constants associated with the coupling of strain gradient to strain gradient24. However, the plethora of higher-order material constants restricts the application of this theory. For simplicity, the flexoelectric theory with rotation gradient effect has also been proposed19,20. Although the number of higher-order material constants has decreased, the effect of other strain gradient components has also been neglected due to the fact that rotation gradient is only the anti-symmetric part of strain gradient. Obviously, it is essential to consider all strain gradient effect, but the number of higher-order material constants need to be decreased for applications.

On the basis of general flexoelectric theory including all strain gradient effects, Li et al.18 reformulated its internal energy density by introducing two sets of independent strain gradient components and demonstrated that there are three independent higher-order material constants associated with the coupling of strain gradient to strain gradient. The same conclusion has also been obtained by Zhou et al.38 in the strain gradient elasticity theory. Then, Ji et al.39 summarized and revisited the decomposition scheme of strain gradient tensor and found that, as a matter of fact, the strain gradient consists of three strain gradient components, \(\eta_{ijk} = \eta_{ijk}^{V} + \eta_{ijk}^{(1)} + \eta_{ijk}^{as}\), in which the strain gradient spherical component \(\eta_{ijk}^{V}\), the deviatoric stretch gradient component \(\eta_{ijk}^{(1)}\) and the symmetric rotation strain gradient component \(\eta_{ijk}^{as}\) are written as

$$\begin{aligned} \eta_{ijk}^{V} & = \frac{1}{10}\delta_{ij} (3\varepsilon_{km,m} - \varepsilon_{mm,k} ) + \frac{1}{10}\delta_{ki} (3\varepsilon_{jm,m} - \varepsilon_{mm,j} ) + \frac{1}{5}\delta_{jk} (2\varepsilon_{mm,i} - \varepsilon_{im,m} ) \\ \eta_{ijk}^{(1)} & = \frac{1}{3}(\varepsilon_{jk,i} + \varepsilon_{ik,j} + \varepsilon_{ij,k} ) \\ & \quad - \frac{1}{15}[\delta_{ij} (2\varepsilon_{km,m} + \varepsilon_{mm,k} ) + \delta_{ki} (2\varepsilon_{jm,m} + \varepsilon_{mm,j} ) + \delta_{kj} (2\varepsilon_{im,m} + \varepsilon_{mm,i} )] \\ \eta_{ijk}^{as} & = \frac{1}{6}[2\varepsilon_{jk,i} - \varepsilon_{ik,j} - \varepsilon_{ij,k} + (e_{ijp} e_{kmn} + e_{ikp} e_{jmn} )\varepsilon_{np,m} ] \\ \end{aligned}$$
(2)

with eijk and δij denoting the alternating tensor and Kronecker delta, respectively. According to the three strain gradient components, the internal energy density of Li et al. is re-written as

$$\begin{aligned} U & = \frac{1}{2}k\varepsilon_{ii} \varepsilon_{jj} + \mu \varepsilon^{\prime}_{ij} \varepsilon^{\prime}_{ij} + 3\mu l_{0}^{2} \eta_{ijk}^{V} \eta_{ijk}^{V} + \mu l_{1}^{2} \eta_{ijk}^{(1)} \eta_{ijk}^{(1)} + 3\mu l_{2}^{2} \eta_{ijk}^{as} \eta_{ijk}^{as} \\ & \quad + \frac{1}{2}\alpha (P_{i} P_{i} + \beta_{1}^{2} Q_{nn} Q_{mm} + \beta_{2}^{2} Q_{ij} Q_{ij} + \beta_{3}^{2} Q_{ij} Q_{ji} ) \\ & \quad + f_{1} P_{i} \eta_{ijj}^{V} + 2f_{2} P_{i} \eta_{jji}^{V} - f_{1} \varepsilon_{nn} Q_{mm} - 2f_{2} \varepsilon_{ij} Q_{ij} \\ \end{aligned}$$
(3)

in which \(\varepsilon^{\prime}_{ij} = \varepsilon_{ij} - \tfrac{1}{3}\delta_{ij} \varepsilon_{nn}\) is the deviatoric strain tensor, k and μ denote the bulk and shear modulus, α denotes the reciprocal dielectric susceptibility, li(i = 0,1,2) and βi(i = 1,2,3) represent the length-scale parameters related to strain gradient and polarization gradient, respectively, f1 and f2 represent the flexocoupling coefficients. It is found that only the spherical component \(\eta_{ijk}^{V}\) can induce polarization in isotropic dielectrics40.

Accordingly, the stress σij, the higher-order stresses \(\tau_{ijk}^{V}\), \(\tau_{ijk}^{(1)}\),\(\tau_{ijk}^{as}\), the effective local electric field Ei and higher-order electric field Vij can be given by the constitutive equations,

$$\sigma_{ij} = k\delta_{ij} \varepsilon_{nn} + 2\mu \varepsilon^{\prime}_{ij} - f_{1} \delta_{ij} Q_{kk} - f_{2} (Q_{ij} { + }Q_{ji} ),$$
(4)
$$\tau_{ijk}^{V} = 6\mu l_{0}^{2} \eta_{ijk}^{V} + f_{1} \delta_{jk} P_{i} + f_{2} (\delta_{ij} P_{k} { + }\delta_{ik} P_{j} ),\tau_{ijk}^{(1)} = 2\mu l_{1}^{2} \eta_{ijk}^{(1)} ,\tau_{ijk}^{as} = 6\mu l_{2}^{2} \eta_{ijk}^{as} ,$$
(5)
$$E_{i} = \alpha P_{i} + f_{1} \eta_{ijj}^{V} + 2f_{2} \eta_{jji}^{V} ,$$
(6)
$$V_{ij} = \alpha (\delta_{ij} \beta_{1}^{2} Q_{kk} + \beta_{2}^{2} Q_{ij} + \beta_{3}^{2} Q_{ji} ) - f_{1} \delta_{ij} \varepsilon_{nn} - 2f_{2} \varepsilon_{ij} .$$
(7)

Based on Eqs. (4)–(7), the internal energy density Eq. (3) can also be expressed as

$$U = \frac{1}{2}\sigma_{ij} \varepsilon_{ij} + \frac{1}{2}\tau_{ijk}^{V} \eta_{ijk}^{V} + \frac{1}{2}\tau_{ijk}^{(1)} \eta_{ijk}^{(1)} + \frac{1}{2}\tau_{ijk}^{as} \eta_{ijk}^{as} + \frac{1}{2}E_{i} P_{i} + \frac{1}{2}V_{ij} Q_{ij} .$$
(8)

The present flexoelectric theory considers all strain gradient effects, polarization gradient effects, direct and inverse flexoelectric effects, and only three material length scale parameters associated with strain gradient are included, which is a general theory with practicability. When the electrical terms are neglected, the flexoelectric theory will reduce to the general strain gradient theory41.

Nonlinear flexoelectric model for circular plate

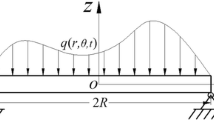
Consider a flexoelectric circular plate as shown in Fig. 1. The thickness of plate is h and the radius is R. The current circular plate is subjected to a transverse load q and an electric voltage V0 between its upper and lower surfaces. The circular plate with specific boundary conditions deforms under the action of external load. A cylindrical coordinate system is adopted to establish its static and dynamic models where rθ plane is consistent with the plate midplane. According to the Kirchhoff assumption, the r-, θ-, z-displacement components are given by

$$u_{r} (r,z,t) = u(r,t) - z\frac{\partial w}{{\partial r}},u_{\theta } (r,z) = 0,u_{z} (r,z) = w(r,t),$$
(9)

where w denotes the transverse deflection, u represents the radial displacement in midplane and t is time. Moreover, the polarization is assumed to be along the thickness direction, given by

$$P_{z} = P_{z} (r,z,t).$$
(10)
Figure 1
figure 1

Schematic of axisymmetric flexoelectric circular plate.

Full size image

From the Von Kármán’s strain theory, the non-vanishing strains take the form

$$\varepsilon_{rr} = \frac{\partial u}{{\partial r}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial r^{2} }},\varepsilon_{\theta \theta } = \frac{u}{r} - \frac{z}{r}\frac{\partial w}{{\partial r}}.$$
(11)

Substituting the nonzero strains Eq. (11) into Eq. (2), these three orthogonal strain gradient components \(\eta_{ijk}^{V}\), \(\eta_{ijk}^{(1)}\) and \(\eta_{ijk}^{as}\) can be obtained and shown in Appendix A. Furthermore, from constitutive relations Eqs. (6) and (7), it can be obtained that,

$$E_{z} = \alpha P_{z} - f_{1} \left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right),$$
(12)
$$V_{zz} = \alpha (\beta_{1}^{2} + \beta_{2}^{2} + \beta_{3}^{2} )Q_{zz} - f_{1} \left( {\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{1}{2}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial r^{2} }} - z\frac{\partial w}{{r\partial r}}} \right).$$
(13)

According to the general governing equations for electroelastic analysis of dielectrics18, Ez and Vzz in Eqs. (12) and (13) satisfy

$$\begin{aligned} & E_{z} - V_{zz,z} + \varphi_{,z} = 0 \\ & - \varepsilon_{0} \varphi_{,zz} + P_{z,z} = 0 \\ \end{aligned}$$
(14)

in which φ is the potential of the Maxwell self-field. It should be noted here that the higher-order electric field Vzr is ignored in comparison with Vzz due to the radial gradient is much smaller than the transverse gradient for thin circular plate. Substituting Eqs. (12) and (13) into Eq. (14), the equilibrium equations for electroelastic analysis of dielectrics are rewritten as

$$\left\{ \begin{gathered} \varphi_{,z} = \alpha \beta^{2} \frac{{\partial^{2} P_{z} }}{{\partial z^{2} }} - \alpha P_{z} + 2f_{1} \left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right) \hfill \\ - \varepsilon_{0} \varphi_{,zz} + \frac{{\partial P_{z} }}{\partial z}{ = }0, \hfill \\ \end{gathered} \right.$$
(15)

where the parameter \(\beta^{2} = \beta_{1}^{2} + \beta_{2}^{2} + \beta_{3}^{2}\) is defined. Combining this governing equations and the electric boundary conditions,

$$\begin{aligned} & at\,\, \, z = \frac{h}{2}:V_{zz} = 0,\varphi \left( \frac{h}{2} \right) = V_{0} \\ & at \, \,\,z = - \frac{h}{2}:V_{zz} = 0,\varphi \left( { - \frac{h}{2}} \right) = 0, \\ \end{aligned}$$
(16)

the polarization and electric potential are obtained and written as

$$\begin{aligned} P_{z} & = \frac{{f_{1} }}{{\alpha \beta^{2} \lambda }}\left( {\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{1}{2}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} } \right)\frac{{e^{\lambda z} - e^{ - \lambda z} }}{{e^{\lambda h/2} + e^{ - \lambda h/2} }} \\ & \quad - \frac{{f_{1} h}}{{2\alpha \beta^{2} \lambda }}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right)\frac{{e^{\lambda z} + e^{ - \lambda z} }}{{e^{\lambda h/2} - e^{ - \lambda h/2} }} + \frac{{1 + 2\alpha \varepsilon_{0} }}{{1 + \alpha \varepsilon_{0} }}\frac{{f_{1} }}{\alpha }\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right) - \frac{{V_{0} }}{\alpha h}, \\ \end{aligned}$$
(17)
$$\begin{aligned} \varphi & = \frac{{f_{1} }}{{1 + \alpha \varepsilon_{0} }}\left[ {\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{1}{2}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} } \right]\left( {\frac{{e^{\lambda z} + e^{ - \lambda z} }}{{e^{\lambda h/2} + e^{ - \lambda h/2} }} - 1} \right) \\ & \quad + \frac{{f_{1} h}}{{2(1 + \alpha \varepsilon_{0} )}}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right)\left( {\frac{2}{h}z - \frac{{e^{\lambda z} - e^{ - \lambda z} }}{{e^{\lambda h/2} - e^{ - \lambda h/2} }}} \right) + \frac{{V_{0} }}{h}z + \frac{{V_{0} }}{2} \\ \end{aligned}$$
(18)

with the parameter λ defined as

$$\lambda { = }\sqrt {\frac{{1 + \alpha \varepsilon_{0} }}{{\varepsilon_{0} \alpha \beta^{2} }}} .$$
(19)

Subsequently, the equilibrium equations and mechanical boundary conditions of the current nonlinear flexoelectric circular plate can be obtained by applying Hamilton’s principle,

$$\delta \int_{{t_{1} }}^{{t_{2} }} {\left( { - 2\pi \int_{0}^{R} {\int_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {Hr{\text{d}}r{\text{d}}z} } + T + W} \right){\text{d}}t} = 0.$$
(20)

The electric enthalpy density H is written as

$$H = U - \frac{1}{2}\varepsilon_{0} \varphi_{,z} \varphi_{,z} + \varphi_{,z} P_{z}$$
(21)

with ε0 denoting the permittivity of a vacuum and U being the internal energy density defined by Eq. (3). The kinetic energy T of the axisymmetric circular plate is

$$T = \pi \rho h\int_{0}^{R} {(\dot{u}^{2} + \dot{w}^{2} )r{\text{d}}r} ,$$
(22)

where ρ represents the mass density, \(\dot{u}\) and \(\dot{w}\) denote the first derivative of radial displacement and deflection versus time, respectively. The work W done by the transverse load q is

$$W = 2\pi \int_{0}^{R} {qw} r{\text{d}}r.$$
(23)

Applying the variational principle of Eq. (20), the equilibrium equations of the nonlinear flexoelectric circular plate are derived as

$$\begin{aligned} & 2(c_{4} - d_{1} )\left( {\frac{u}{{r^{2} }} - \frac{\partial u}{{r\partial r}} - \frac{{\partial^{2} u}}{{\partial r^{2} }} - \frac{\partial w}{{\partial r}}\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right) - \frac{{c_{4} }}{r}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} + c_{5} \frac{1}{r}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} + 2c_{7} \left[ {\frac{{\partial^{4} u}}{{\partial r^{4} }} + 2\frac{{\partial^{3} u}}{{r\partial r^{3} }}} \right. \\ & \quad \left. { - 3\frac{{\partial^{2} u}}{{r^{2} \partial r^{2} }} + 3\frac{\partial u}{{r^{3} \partial r}} - 3\frac{u}{{r^{4} }} + \frac{{\partial^{2} w}}{{\partial r^{2} }}\left( {2\frac{{\partial^{2} w}}{{r\partial r^{2} }} + 3\frac{{\partial^{3} w}}{{\partial r^{3} }}} \right) + \frac{\partial w}{{\partial r}}\left( {\frac{{\partial^{4} w}}{{\partial r^{4} }} + 2\frac{{\partial^{3} w}}{{r\partial r^{3} }} - 2\frac{{\partial^{2} w}}{{r^{2} \partial r^{2} }}} \right)} \right] \\ & \quad + c_{9} \left( {\frac{\partial w}{{r^{2} \partial r}}\frac{{\partial^{2} w}}{{\partial r^{2} }} - \frac{1}{r}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right)^{2} - \frac{1}{r}\frac{\partial w}{{\partial r}}\frac{{\partial^{3} w}}{{\partial r^{3} }}} \right) + \rho \ddot{u} = 0, \\ \end{aligned}$$
(24)
$$\begin{aligned} & \frac{{c_{7} h^{3} }}{6}\nabla^{6} w - \left( {\frac{{c_{4} h^{3} }}{6} + 2c_{1} h - d_{2} } \right)\nabla^{4} w - 4c_{2} h\left( {\frac{\partial w}{{r\partial r}}} \right)^{2} \left( {\frac{\partial w}{{r\partial r}} - 3\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right) \\ & \quad + (c_{4} - d_{1} )h\left[ {2\frac{{\partial^{2} u}}{{\partial r^{2} }}\frac{\partial w}{{\partial r}} + 2\frac{\partial u}{{\partial r}}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right) + \left( {\frac{\partial w}{{\partial r}}} \right)^{2} \left( {3\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right)} \right] + 2h(c_{5} - d_{1} )\left( {\frac{\partial u}{{\partial r}}\frac{\partial w}{{r\partial r}} + \frac{u}{r}\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right) \\ & \quad - {2}c_{7} h\left[ {\frac{{\partial^{4} u}}{{\partial r^{4} }}\frac{\partial w}{{\partial r}} + \frac{{\partial^{3} u}}{{\partial r^{3} }}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + 2\frac{\partial w}{{r\partial r}}} \right) + \frac{{\partial^{2} u}}{{\partial r^{2} }}\frac{{\partial^{2} w}}{{r\partial r^{2} }} + 3\frac{\partial w}{{r\partial r}}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right)^{2} + 2\left( {\frac{\partial w}{{\partial r}}} \right)^{2} \frac{{\partial^{3} w}}{{r\partial r^{3} }}} \right. \\ & \quad \left. { + \left( {\frac{\partial w}{{\partial r}}} \right)^{2} \frac{{\partial^{4} w}}{{\partial r^{4} }} + \left( {\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right)^{3} + 4\frac{\partial w}{{\partial r}}\frac{{\partial^{2} w}}{{\partial r^{2} }}\frac{{\partial^{3} w}}{{\partial r^{3} }}} \right] + 4c_{8} h\left[ {\frac{{\partial^{2} u}}{{r^{2} \partial r^{2} }}\frac{\partial w}{{\partial r}} + \left( {\frac{\partial u}{{r^{2} \partial r}} - \frac{u}{{r^{3} }}} \right)\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} - 2\frac{\partial w}{{r\partial r}}} \right)} \right] \\ & \quad + c_{9} h\left[ { - \frac{{\partial^{3} u}}{{\partial r^{3} }}\frac{\partial w}{{r\partial r}} - \frac{{\partial^{2} u}}{{r\partial r^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} - 3\frac{\partial w}{{r\partial r}}} \right) + 3\left( {\frac{\partial u}{{r^{2} \partial r}} - \frac{u}{{r^{3} }}} \right)\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} - 2\frac{\partial w}{{r\partial r}}} \right)} \right] - \rho h\ddot{w} + q = 0 \\ \end{aligned}$$
(25)

with

$$\nabla^{6} = \frac{{\partial^{6} }}{{\partial r^{6} }} + \frac{3}{r}\frac{{\partial^{5} }}{{\partial r^{5} }} - \frac{3}{{r^{2} }}\frac{{\partial^{4} }}{{\partial r^{4} }} + \frac{6}{{r^{3} }}\frac{{\partial^{3} }}{{\partial r^{3} }} - \frac{9}{{r^{4} }}\frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{9}{{r^{5} }}\frac{\partial }{\partial r}\quad \nabla^{4} = \frac{{\partial^{4} }}{{\partial r^{4} }} + \frac{2}{r}\frac{{\partial^{3} }}{{\partial r^{3} }} - \frac{1}{{r^{2} }}\frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{1}{{r^{3} }}\frac{\partial }{\partial r}$$
(26)

and the coefficients \(c_{i} (i = 1,2,3, \ldots 9)\), d1 and d2 are given by

$$\begin{aligned} & d_{1} = \frac{{f_{1}^{2} \varepsilon_{0} \lambda }}{{h(1 + \alpha \varepsilon_{0} )}}\frac{{e^{\lambda h/2} - e^{ - \lambda h/2} }}{{e^{\lambda h/2} + e^{ - \lambda h/2} }},d_{2} = \frac{{f_{1}^{2} h}}{{\alpha (1 + \alpha \varepsilon_{0} )}}\left( {1 + \frac{{\lambda h\alpha \varepsilon_{0} }}{2}\frac{{e^{\lambda h/2} + e^{ - \lambda h/2} }}{{e^{\lambda h/2} - e^{ - \lambda h/2} }}} \right) \\ & c_{1} = \frac{6}{5}\mu l_{0}^{2} + \frac{4}{15}\mu l_{1}^{2} + \mu l_{2}^{2} ,c_{2} = \frac{{9}}{{{20}}}\mu l_{0}^{2} + \frac{4}{15}\mu l_{1}^{2} + \frac{1}{4}\mu l_{2}^{2} \\ & c_{3} = \frac{12}{5}\mu l_{0}^{2} - \frac{2}{15}\mu l_{1}^{2} - 2\mu l_{2}^{2} ,c_{4} = \frac{1}{2}\frac{E}{{1 - v^{2} }},c_{5} = \frac{1}{2}\frac{Ev}{{1 - \nu^{2} }} \\ & c_{6} = \frac{6}{5}\mu l_{0}^{2} - \frac{7}{5}\mu l_{1}^{2} ,c_{7} = \frac{9}{5}\mu l_{0}^{2} + \frac{2}{5}\mu l_{1}^{2} ,c_{8} = \frac{3}{5}\mu l_{0}^{2} + \frac{4}{5}\mu l_{1}^{2} ,c_{9} = \frac{6}{5}\mu l_{0}^{2} - \frac{2}{5}\mu l_{1}^{2} \\ \end{aligned}$$
(27)

in which E and v denote the Young’s modulus and the Poisson ratio, respectively. The initial conditions are written as

$$\rho h\dot{u}\delta u|_{{t_{1} }}^{{t_{2} }} = 0,\rho h\dot{w}\delta w|_{{t_{1} }}^{{t_{2} }} = 0.$$
(28)

The mechanical boundary conditions satisfy

$$\begin{aligned} & S_{u} (R)\delta u(R) - S_{u} (0)\delta u(0) = 0,S_{u1} (R)\delta u_{,r} (R) - S_{u1} (0)\delta u_{,r} (0) = 0 \\ & S_{w} (R)\delta w(R) - S_{w} (0)\delta w(0) = 0,S_{w1} (R)\delta w_{,r} (R) - S_{w1} (0)\delta w_{,r} (0) = 0 \\ & S_{w2} (R)\delta w_{,rr} (R) - S_{w2} (0)\delta w_{,rr} (0) = 0, \\ \end{aligned}$$
(29)

where Su, Su1, Sw, Sw1, Sw2 are shown in Appendix B.

When we ignore all the nonlinear terms, the nonlinear flexoelectric model will reduce to the corresponding linear model of circular plate. In the linear model, the polarization and electrical potential are shown, respectively, as

$$P_{z} = - \frac{{f_{1} h}}{{2\alpha \beta^{2} \lambda }}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right)\frac{{e^{\lambda z} + e^{ - \lambda z} }}{{e^{\lambda h/2} - e^{ - \lambda h/2} }} + \frac{{1 + 2\alpha \varepsilon_{0} }}{{1 + \alpha \varepsilon_{0} }}\frac{{f_{1} }}{\alpha }\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right) - \frac{{V_{0} }}{\alpha h},$$
(30)
$$\varphi = \frac{{f_{1} h}}{{2(1 + \alpha \varepsilon_{0} )}}\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{{r\partial r}}} \right)\left( {\frac{2}{h}z - \frac{{e^{\lambda z} - e^{ - \lambda z} }}{{e^{\lambda h/2} - e^{ - \lambda h/2} }}} \right) + \frac{{V_{0} }}{h}z + \frac{{V_{0} }}{2}.$$
(31)

The governing equation is written as

$$\frac{{c_{7} h^{3} }}{6}\nabla^{6} w - \left( {\frac{{c_{4} h^{3} }}{6} + 2c_{1} h - d_{2} } \right)\nabla^{4} w - \rho h\ddot{w} + q = 0.$$
(32)

And the mechanical boundary conditions are

$$\begin{aligned} & S_{w}^{L} (R)\delta w(R) - S_{w}^{L} (0)\delta w(0) = 0 \\ & S_{w1}^{L} (R)\delta w_{,r} (R) - S_{w1}^{L} (0)\delta w_{,r} (0) = 0 \\ & S_{w2}^{L} (R)\delta w_{,rr} (R) - S_{w2}^{L} (0)\delta w_{,rr} (0) = 0, \\ \end{aligned}$$
(33)

where

$$\begin{aligned} S_{w}^{L} (r) & = r\left[ {\frac{{c_{7} h^{3} }}{6}\left( {\frac{{\partial^{5} w}}{{\partial r^{5} }} + 2\frac{{\partial^{4} w}}{{r\partial r^{4} }} - 3\frac{{\partial^{3} w}}{{r^{2} \partial r^{3} }} + 3\frac{{\partial^{2} w}}{{r^{3} \partial r^{2} }} - 3\frac{\partial w}{{r^{4} \partial r}}} \right) - \left( {2c_{1} h + \frac{{c_{4} h^{3} }}{6} - d_{2} } \right)\left( {\frac{{\partial^{3} w}}{{\partial r^{3} }} + \frac{{\partial^{2} w}}{{r\partial r^{2} }} - \frac{\partial w}{{r^{2} \partial r}}} \right)} \right] \\ S_{w1}^{L} (r) & = r\left[ { - \frac{{c_{7} h^{3} }}{6}\left( {\frac{{\partial^{4} w}}{{\partial r^{4} }} + \frac{{\partial^{3} w}}{{r\partial r^{3} }}} \right) + \frac{{(2c_{8} + c_{9} )h^{3} }}{4}\left( {\frac{{\partial^{2} w}}{{r^{2} \partial r^{2} }} - \frac{\partial w}{{r^{3} \partial r}}} \right) + \left( {2c_{1} h + \frac{{c_{4} h^{3} }}{6} - d_{2} } \right)\frac{{\partial^{2} w}}{{\partial r^{2} }}} \right. \\ & \quad \left. { + \left( {c_{3} h + \frac{{c_{5} h^{3} }}{6} - d_{2} } \right)\frac{\partial w}{{r\partial r}} + \frac{{f_{1} }}{\alpha }V_{0} } \right] \\ S_{w2}^{L} (r) & = r\left[ {\frac{{c_{7} h^{3} }}{6}\frac{{\partial^{3} w}}{{\partial r^{3} }} + \frac{{c_{9} h^{3} }}{4}\left( {\frac{{\partial^{2} w}}{{r\partial r^{2} }} - \frac{\partial w}{{r^{2} \partial r}}} \right)} \right]. \\ \end{aligned}$$
(34)

The present nonlinear model of flexoelectric circular plate has been given in Eqs. (24)–(29) which can be further converted into proper dimensionless indexes. By introducing dimensionless parameters,

$$\xi = \frac{r}{R},\overline{w} = \frac{w}{h},\overline{u} = \frac{u}{h},\vartheta = \frac{h}{R},\overline{q}_{0} = \frac{q}{{\vartheta^{4} (c_{4} - d_{1} )}},\varsigma = \sqrt {\frac{{c_{4} - d_{1} }}{{\rho R^{2} }}} t,\overline{V}_{0} = \frac{{R^{2} f_{1} V_{0} }}{{\alpha h^{4} (c_{4} - d_{1} )}}$$
(35)

the governing equations are normalized as

$$\begin{aligned} & 2\frac{{\overline{u}}}{{\xi^{2} }} - 2\frac{{\partial \overline{u}}}{\xi \partial \xi } - 2\frac{{\partial^{2} \overline{u}}}{{\partial \xi^{2} }} - \frac{{\vartheta b_{0} }}{\xi }\left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} + \vartheta b_{2} \left( {\frac{{\partial \overline{w}}}{{\xi^{2} \partial \xi }}\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} - \frac{1}{\xi }\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{2} - \frac{{\partial \overline{w}}}{\xi \partial \xi }\frac{{\partial^{3} \overline{w}}}{{\partial \xi^{3} }}} \right) \\ & \quad - 2\vartheta \frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + \frac{{\vartheta b_{1} }}{\xi }\left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} + 2b_{3} \left( {\frac{{\partial^{4} \overline{u}}}{{\partial \xi^{4} }} + 2\frac{{\partial^{3} \overline{u}}}{{\xi \partial \xi^{3} }} - 3\frac{{\partial^{2} \overline{u}}}{{\xi^{2} \partial \xi^{2} }} + 3\frac{{\partial \overline{u}}}{{\xi^{3} \partial \xi }} - 3\frac{{\overline{u}}}{{\xi^{4} }}} \right) \\ & \quad + 2\vartheta b_{3} \left( {\frac{2}{\xi }\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{2} + \frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + 3\frac{{\partial^{3} \overline{w}}}{{\partial \xi^{3} }}\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + 2\frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} - 2\frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{2} \overline{w}}}{{\xi^{2} \partial \xi^{2} }}} \right) + \frac{{\partial^{2} \overline{u}}}{{\partial \varsigma^{2} }} = 0, \\ \end{aligned}$$
(36)
$$\begin{aligned} & \frac{{b_{3} }}{6}\left( {\frac{{\partial^{6} \overline{w}}}{{\partial \xi^{6} }} + 3\frac{{\partial^{5} \overline{w}}}{{\xi \partial \xi^{5} }} - 3\frac{{\partial^{4} \overline{w}}}{{\xi^{2} \partial \xi^{4} }} + 6\frac{{\partial^{3} \overline{w}}}{{\xi^{3} \partial \xi^{3} }} - 9\frac{{\partial^{2} \overline{w}}}{{\xi^{4} \partial \xi^{2} }} + 9\frac{{\partial \overline{w}}}{{\xi^{5} \partial \xi }}} \right) - b_{4} \left( {\frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + 2\frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} - \frac{{\partial^{2} \overline{w}}}{{\xi^{2} \partial \xi^{2} }} + \frac{{\partial \overline{w}}}{{\xi^{3} \partial \xi }}} \right) \\ & \quad + \frac{2}{\vartheta }\left[ {\frac{{\partial^{2} \overline{u}}}{{\partial \xi^{2} }}\frac{{\partial \overline{w}}}{\partial \xi } + \frac{{\partial \overline{u}}}{\partial \xi }\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + \frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)} \right] + \left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \left( {3\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + \frac{{\partial \overline{w}}}{\xi \partial \xi }} \right) + \frac{{2b_{9} }}{\vartheta }\left( {\frac{{\partial \overline{u}}}{\partial \xi }\frac{{\partial \overline{w}}}{\xi \partial \xi } + \frac{{\overline{u}}}{\xi }\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right) \\ & \quad - 4b_{5} \left( {\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)^{2} \left( {\frac{{\partial \overline{w}}}{\xi \partial \xi } - 3\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right) - \frac{{{2}b_{3} }}{\vartheta }\left[ {\frac{{\partial^{4} \overline{u}}}{{\partial \xi^{4} }}\frac{{\partial \overline{w}}}{\partial \xi } + \frac{{\partial^{3} \overline{u}}}{{\partial \xi^{3} }}\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + 2\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right) + \frac{{\partial^{2} \overline{u}}}{{\partial \xi^{2} }}\frac{{\partial^{2} \overline{w}}}{{\xi \partial \xi^{2} }}} \right] \\ & \quad - {2}b_{3} \left[ {3\frac{{\partial \overline{w}}}{\xi \partial \xi }\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{2} + 2\left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} + \left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + \left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{3} + 4\frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}\frac{{\partial^{3} \overline{w}}}{{\partial \xi^{3} }}} \right] \\ & \quad + 4\frac{{b_{6} }}{\vartheta }\left[ {\frac{{\partial^{2} \overline{u}}}{{\xi^{2} \partial \xi^{2} }}\frac{{\partial \overline{w}}}{\partial \xi } + \left( {\frac{{\partial \overline{u}}}{{\xi^{2} \partial \xi }} - \frac{{\overline{u}}}{{\xi^{3} }}} \right)\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} - 2\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)} \right] + \frac{{b_{2} }}{\vartheta }\left[ { - \frac{{\partial^{3} \overline{u}}}{{\partial \xi^{3} }}\frac{{\partial \overline{w}}}{\xi \partial \xi } - \frac{{\partial^{2} \overline{u}}}{{\xi \partial \xi^{2} }}\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} - 3\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)} \right. \\ & \quad \left. { + 3\left( {\frac{{\partial \overline{u}}}{{\xi^{2} \partial \xi }} - \frac{{\overline{u}}}{{\xi^{3} }}} \right)\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} - 2\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)} \right] - \frac{1}{{\vartheta^{2} }}\frac{{\partial^{2} \overline{w}}}{{\partial \varsigma^{2} }} + \overline{q}_{0} = 0 \\ \end{aligned}$$
(37)

the dimensionless initial conditions are

$$\dot{\overline{u}}\delta \overline{u}|_{{\varsigma_{1} }}^{{\varsigma_{2} }} = 0,\dot{\overline{w}}\delta \overline{w}|_{{\varsigma_{1} }}^{{\varsigma_{2} }} = 0,$$
(38)

and the boundary conditions are reformulated as

$$\begin{aligned} & \overline{S}_{u} (1)\delta \overline{u}(1) - \overline{S}_{u} (0)\delta \overline{u}(0) = 0,\overline{S}_{u1} (1)\delta \overline{u}_{,\xi } (1) - \overline{S}_{u1} (0)\delta \overline{u}_{,\xi } (0) = 0 \\ & \overline{S}_{w} (1)\delta \overline{w}(1) - \overline{S}_{w} (0)\delta \overline{w}(0) = 0,\overline{S}_{w1} (1)\delta \overline{w}_{,\xi } (1) - \overline{S}_{w1} (0)\delta \overline{w}_{,\xi } (0) = 0 \\ & \overline{S}_{w2} (1)\delta \overline{w}_{,\xi \xi } (1) - \overline{S}_{w2} (0)\delta \overline{w}_{,\xi \xi } (0) = 0, \\ \end{aligned}$$
(39)

where the parameters bi(i = 1 ~ 9) are given by

$$\begin{aligned} & b_{0} = \frac{{c_{4} }}{{c_{4} - d_{1} }},b_{1} = \frac{{c_{5} }}{{c_{4} - d_{1} }},b_{2} = \frac{{c_{9} }}{{R^{2} (c_{4} - d_{1} )}},b_{3} = \frac{{c_{7} }}{{R^{2} (c_{4} - d_{1} )}},b_{4} = \frac{{c_{4} h^{3} + 12c_{1} h - 6d_{2} }}{{6h^{3} (c_{4} - d_{1} )}} \\ & b_{5} = \frac{{c_{2} }}{{R^{2} (c_{4} - d_{1} )}}, b_{6} = \frac{{c_{8} }}{{R^{2} (c_{4} - d_{1} )}}, b_{7} = \frac{{c_{9} }}{{2c_{7} }},b_{8} = \frac{{c_{3} h - d_{2} }}{{h^{3} (c_{4} - d_{1} )}},b_{9} = \frac{{c_{5} - d_{1} }}{{c_{4} - d_{1} }} \\ \end{aligned}$$
(40)

and the dimensionless quantities \(\overline{S}_{u}\), \(\overline{S}_{u1}\), \(\overline{S}_{w}\), \(\overline{S}_{w1}\), \(\overline{S}_{w2}\) are given in Appendix B.

Nonlinear bending of flexoelectric circular plate

The differential quadrature method (DQM)42,43,44 can be used to solve the nonlinear governing equations (36) and (37) with the corresponding boundary conditions for the axisymmetric bending of flexoelectric circular plate. For a function f(x), its k-order partial derivatives with respect to x at any sample point can be written as

$$\frac{{\partial^{k} f(x_{i} )}}{{\partial x^{k} }} = \sum\limits_{j = 1}^{N} {A_{ij}^{(k)} f(x_{j} )}$$
(41)

with N denoting the total number of discrete points and \(A_{ij}^{(k)}\) being the k-order weighting coefficients matrix whose recursion formula can be found in Li et al.41. The normalized Gauss–Chebyshev–Lobatto points are used to generate the DQM point system,

$$\xi (i) = \frac{1}{2}\left[ {1 - \cos \left( {\frac{i - 1}{{N - 1}}\pi } \right)} \right],\quad i = 1,2, \ldots ,N.$$
(42)

By applying DQM, the discretized equilibrium equations are given as

$$\begin{aligned} & \left( {\frac{2}{{\xi_{i}^{2} }} - \frac{{6b_{3} }}{{\xi_{i}^{4} }}} \right)\overline{u}_{i} + \left( {\frac{{6b_{3} }}{{\xi_{i}^{3} }} - \frac{2}{{\xi_{i} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{u}_{j} } - \left( {2 + \frac{{6b_{3} }}{{\xi_{i}^{2} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{u}_{j} } + \frac{{4b_{3} }}{{\xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{u}_{j} } + 2b_{3} \sum\limits_{j = 1}^{N} {A_{ij}^{(4)} \overline{u}_{j} } \\ & \quad + \left( {\frac{{\vartheta b_{1} }}{{\xi_{i} }} - \frac{{\vartheta b_{0} }}{{\xi_{i} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } + \left( {\frac{{\vartheta b_{2} }}{{\xi_{i}^{2} }} - \frac{{4\vartheta b_{3} }}{{\xi_{i}^{2} }} - 2\vartheta } \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \\ & \quad + \left( {\frac{{4\vartheta b_{3} }}{{\xi_{i} }} - \frac{{\vartheta b_{2} }}{{\xi_{i} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } + \left( {\frac{{4\vartheta b_{3} }}{{\xi_{i} }} - \frac{{\vartheta b_{2} }}{{\xi_{i} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{w}_{j} } \\ & \quad + 2\vartheta b_{3} \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(4)} \overline{w}_{j} } + 6\vartheta b_{3} \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{w}_{j} } + \frac{{\partial^{2} \overline{u}_{i} }}{{\partial \varsigma^{2} }} = 0, \\ \end{aligned}$$
(43)
$$\begin{aligned} & \frac{{b_{3} }}{6}\sum\limits_{j = 1}^{N} {A_{ij}^{(6)} \overline{w}_{j} } + \frac{1}{2}\frac{{b_{3} }}{{\xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(5)} \overline{w}_{j} } - \left( {\frac{1}{2}\frac{{b_{3} }}{{\xi_{i}^{2} }} + b_{4} } \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(4)} \overline{w}_{j} } + \left( {\frac{{b_{3} }}{{\xi_{i}^{3} }} - \frac{{2b_{4} }}{{\xi_{i} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{w}_{j} } \\ & \quad + \left( {\frac{{b_{4} }}{{\xi_{i}^{2} }} - \frac{3}{2}\frac{{b_{3} }}{{\xi_{i}^{4} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } + \left( {\frac{3}{2}\frac{{b_{3} }}{{\xi_{i}^{5} }} - \frac{{b_{4} }}{{\xi_{i}^{3} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } + \left( {\frac{1}{{\xi_{i} }} - \frac{{4b_{5} }}{{\xi_{i}^{3} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \\ & \quad + \left( {3 + \frac{{12b_{5} }}{{\xi_{i}^{2} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } - \frac{{6b_{3} }}{{\xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \\ & \quad - \frac{{4b_{3} }}{{\xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{w}_{j} } - 2b_{3} \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(4)} \overline{w}_{j} } \\ & \quad - 2b_{3} \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } - 8b_{3} \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{w}_{j} } \\ & \quad + \frac{{2(3b_{2} + 4b_{6} )}}{\vartheta }\frac{{\overline{u}_{i} }}{{\xi_{i}^{4} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } + \left( {2b_{9} - \frac{{3b_{2} + 4b_{6} }}{{\xi_{i}^{2} }}} \right)\frac{{\overline{u}_{i} }}{{\vartheta \xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \\ & \quad + \frac{2}{{\vartheta \xi_{i} }}\left( {1 + b_{9} - \frac{{3b_{2} + 4b_{6} }}{{\xi_{i}^{2} }}} \right)\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } - \frac{{{2}b_{3} + b_{2} }}{{\vartheta \xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } \\ & \quad + \frac{1}{\vartheta }\left( {\frac{{3b_{2} + 4b_{6} }}{{\xi_{i}^{2} }} + 2} \right)\left( {\sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } + \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } } \right) \\ & \quad - \frac{{4b_{3} + b_{2} }}{{\vartheta \xi_{i} }}\sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } - \frac{{{2}b_{3} }}{\vartheta }\sum\limits_{j = 1}^{N} {A_{ij}^{(4)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(1)} \overline{w}_{j} } - \frac{{{2}b_{3} }}{\vartheta }\sum\limits_{j = 1}^{N} {A_{ij}^{(3)} \overline{u}_{j} } \sum\limits_{j = 1}^{N} {A_{ij}^{(2)} \overline{w}_{j} } - \frac{1}{{\vartheta^{2} }}\frac{{\partial^{2} \overline{w}_{i} }}{{\partial \varsigma^{2} }} = - \overline{q}_{0} \\ \end{aligned}$$
(44)

And the discretized dimensionless quantities \(\overline{S}_{u}\), \(\overline{S}_{u1}\), \(\overline{S}_{w}\), \(\overline{S}_{w1}\), \(\overline{S}_{w2}\) of the boundary conditions Eq. (39) are given in Appendix Eqs. (B.11)–(B.15), respectively.

By denoting the displacement vector as

$${\mathbf{d}} = \{ \{ \overline{u}_{i} \}^{T} ,\{ \overline{w}_{i} \}^{T} \}^{T} ,\quad i = 1,2, \ldots ,N.$$
(45)

Then the discrete governing equations Eqs. (43) and (44), together with the boundary conditions, can be written in matrix form

$$({\mathbf{K}}_{{\mathbf{L}}} + {\mathbf{K}}_{{{\mathbf{NL}}}} ){\mathbf{d}} + {\mathbf{M\ddot{d}}} = {\mathbf{F}}$$
(46)

in which KL and KNL represent equivalent linear and nonlinear stiffness matrices, M denotes the mass matrix and F denotes the external force vector.

Solution of simply supported circular plate

For the nonlinear static bending of axisymmetric flexoelectric circular plate subjected to a uniformly distributed load q and a constant electric voltage V0 between its upper and lower surfaces, the corresponding discrete equilibrium equations and boundary conditions simplified from Eq. (46) are given by

$$({\mathbf{K}}_{{\mathbf{L}}} + {\mathbf{K}}_{{{\mathbf{NL}}}} ){\mathbf{d}} = {\mathbf{F}}.$$
(47)

For the simply supported axisymmetric circular plate, its boundary conditions are

$$\overline{u}(\xi_{N} ) = 0,\overline{w}(\xi_{N} ) = 0,\overline{S}_{u1} (\xi_{N} ) = 0,\overline{S}_{w1} (\xi_{N} ) = 0,\overline{S}_{w2} (\xi_{N} ) = 0.$$
(48)

And the regularity conditions are listed as

$$\overline{u}(\xi_{1} ) = 0,\overline{w}_{,\xi } (\xi_{1} ) = 0.$$
(49)

These nonlinear equations can be solved according to Newton–Raphson method. Of course, the linear axisymmetric bending of flexoelectric circular plate can also be solved from Eqs. (32)–(34) by DQM. In addition, as a contrast, the theoretical solution of linear axisymmetric bending is derived as41

$$\overline{w} = a_{1} + a_{2} \xi^{2} + a_{5} I_{0} (s\xi ) + \frac{{\overline{q}_{0} \xi^{4} }}{{64b_{4} }},$$
(50)

where the underdetermined coefficients are given by

$$a_{1} { = }\frac{{\overline{q}_{0} }}{{8b_{4} }}\left[ {\frac{{(b_{7} + 1)I_{0} (s)}}{{g_{1} }} - \frac{1 + 8p}{8}} \right],a_{2} = \frac{{\overline{q}_{0} p}}{{8b_{4} }},a_{5} = \overline{ - }\frac{{\overline{q}_{0} (b_{7} + 1)}}{{8b_{4} g_{1} }},$$
(51)

where the coefficients s, p, g1 are given by

$$\begin{aligned} & s = \sqrt {\frac{{6b_{4} }}{{b_{3} }}} ,p = \frac{3}{{b_{1} + 6b_{4} + 6b_{8} }}\left( {\frac{{g_{3} }}{2}{ + }\frac{{(2b_{7} + 1)g_{2} }}{{g_{1} }}} \right) \\ & g_{1} = \frac{{b_{7} s^{2} }}{2}(I_{0} (s) + I_{2} (s)) + s\left( {\frac{{s^{2} }}{4} - b_{7} } \right)I_{1} (s) + \frac{{s^{3} }}{12}I_{3} (s) \\ & g_{2} = \frac{{s^{2} (b_{2} + b_{4} + 2b_{6} )}}{8}I_{0} (s) + g_{0} sI_{1} (s) + \frac{{s^{2} (b_{2} + 2b_{6} )}}{8}I_{2} (s) - \frac{{b_{4} }}{4}sI_{3} (s) - \frac{{b_{3} s^{4} }}{48}I_{4} (s) \\ & g_{3} = - \frac{1}{6}b_{1} - \frac{1}{2}b_{2} + 2b_{3} - 3b_{4} - b_{6} - b_{8} - \overline{V}_{0} \frac{{16b_{4} }}{{q_{0} }} \\ & g_{0} = \frac{1}{12}(2b_{1} - 3b_{2} - 9b_{4} - 6b_{6} + 12b_{8} ) \\ \end{aligned}$$
(52)

and Ik (k = 0,1,…,4) represent the k-order modified Bessel functions of the first kind.

Discussions

In order to illustrate the current solution, a polyvinylidene difluoride (PVDF) axisymmetric circular plate is considered with its properties: E = 3.7 GPa, α = 1.38 × 1010 N m2/C2, ε0 = 8.854 × 10−12C2/(N m2), f = − 179 N m/C, ρ = 1.78 × 103 kg/m3. The radius of the circular plate is set as 10 times the thickness and the length-scale parameters are assumed to be 1 μm.

The dimensionless deflection is shown in Fig. 2 with the transverse load q being 1 μN/μm2 and the electric voltage V0 being 100 V. In Fig. 2, the static bending deflection of axisymmetric flexoelectric circular plate is small compared with its thickness, and the numerical results based on the linear and nonlinear models agree well with each other. This demonstrates that the accuracy of the linear model is sufficient for small deflection question. In addition, the numerical results agree well with the linear theoretical results. The DQM is suitable for solving the current problem.

Figure 2
figure 2

The bending deflection with q = 1 μN/μm2 and V0 = 100 V.

Full size image

When the static bending deflection is comparable to the thickness of plate, the linear model does not work and we have to adopt the nonlinear model. The dimensionless nonlinear displacements are shown in Fig. 3 under different loads. Figure 3 shows the maximum deflection is about 30 ~ 60 times of that of maximum radial displacement. The radial displacement is small and can be neglected compared with its lateral deflection. From Fig. 3a, it can be found that the dimensionless deflection increases with the increase of transverse load q, while the dimensionless deflection decreases with the increase of electric voltage V0. This is because the transverse load q and the electric voltage V0 generate an opposite bending deformation. The final result is a superposition of these two parts. In order to investigate the bending deflection induced by the inverse flexoelectric effect in detail, the dimensionless deflection of axisymmetric circular plate subjected to an electric voltage V0 only between the upper and lower surfaces of the plate is shown in Fig. 4. The bending deflection induced by the inverse flexoelectric effect is small and opposite in comparison with that generated by transverse load q. Furthermore, the inverse flexoelectric effect strengthens as the thickness of plate decreases, which can be further enhanced as the thickness of flexoelectric circular plate reaches nanometer scale.

Figure 3
figure 3

The dimensionless nonlinear displacements under different loads (a) the bending deflection, (b) the corresponding radial displacement.

Full size image
Figure 4
figure 4

The dimensionless nonlinear bending deflections induced by inverse flexoelectric effect with q=0 and V0=1000 V for circular plate of different thickness.

Full size image

Figure 5 reveals the influence of strain gradient stiffening effect on the dimensionless bending deflection in the inverse flexoelectric process. When the plate thickness is comparable with the material length scale parameter, the dimensionless deflection with l0 = l1 = l2 ≠ 0 (including all strain gradient stiffening effect) is far smaller than that with l0 = l1 = l2 = 0 (ignoring all the strain gradient stiffening effect). This demonstrates the stiffening effect of strain gradient is remarkable. When the plate thickness is far great than the material length scale parameter, the dimensionless deflection with l0 = l1 = l2 ≠ 0 is close to that with l0 = l1 = l2 = 0. This demonstrates that the stiffening effect of strain gradient is negligible in comparison with the traditional plate bending rigidity. Moreover, the stiffening effects of the strain gradient spherical component (l0 ≠ 0), the deviatoric stretch gradient component (l1 ≠ 0), the symmetric rotation strain gradient component (l2 ≠ 0) are examined separately. Figure 5 shows that the strain gradient spherical component (l0 ≠ 0) dominates the stiffening effect, while the symmetric rotation strain gradient component (l2 ≠ 0) exhibits the least stiffening effect.

Figure 5
figure 5

The dimensionless nonlinear bending deflections with q=0 and V0=1000 V (a) \(h = 1\) μm, (b) \(h = 5\) μm, (c) \(h = 10\) μm, (d) \(h = 20\) μm.

Full size image

The distribution of electric potential is also investigated in Fig. 6. When q = 0, the electric potential is uniformly distributed along the thickness and is constant along the radius. In fact, the electric potential can be significantly affected by the transverse load q. The larger the load, the more uneven the potential distribution will be. This is because the bending deformation of circular plate under transverse load q can induce polarization and electric potential by direct flexoelectric effect. The greater the strain gradient, the greater the induced polarization and electric potential will be.

Figure 6
figure 6

The distribution of electric potential with V0=10 V (a) thickness direction, (b) radial direction.

Full size image

Nonlinear free vibration of axisymmetric flexoelectric circular plate

From the static bending analysis of axisymmetric flexoelectric circular plate, it can be obtained from Fig. 3 that the radial displacement is small and can be neglected compared with its lateral deflection. Thus, for the nonlinear free vibration problem of axisymmetric flexoelectric circular plate, the effect of the radial displacement on the lateral vibration is neglected for simplicity and the governing equation reduced from Eq. (37) is given by

$$\begin{aligned} & \frac{{b_{3} }}{6}\left( {\frac{{\partial^{6} \overline{w}}}{{\partial \xi^{6} }} + 3\frac{{\partial^{5} \overline{w}}}{{\xi \partial \xi^{5} }} - 3\frac{{\partial^{4} \overline{w}}}{{\xi^{2} \partial \xi^{4} }} + 6\frac{{\partial^{3} \overline{w}}}{{\xi^{3} \partial \xi^{3} }} - 9\frac{{\partial^{2} \overline{w}}}{{\xi^{4} \partial \xi^{2} }} + 9\frac{{\partial \overline{w}}}{{\xi^{5} \partial \xi }}} \right) - b_{4} \left( {\frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + 2\frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} - \frac{{\partial^{2} \overline{w}}}{{\xi^{2} \partial \xi^{2} }} + \frac{{\partial \overline{w}}}{{\xi^{3} \partial \xi }}} \right) \\ & \quad + \left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \left( {3\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + \frac{{\partial \overline{w}}}{\xi \partial \xi }} \right) - 4b_{5} \left( {\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)^{2} \left( {\frac{{\partial \overline{w}}}{\xi \partial \xi } - 3\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right) \\ & \quad - {2}b_{3} \left[ {3\frac{{\partial \overline{w}}}{\xi \partial \xi }\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{2} + 2\left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} + \left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + \left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{3} + 4\frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}\frac{{\partial^{3} \overline{w}}}{{\partial \xi^{3} }}} \right] - \frac{1}{{\vartheta^{2} }}\frac{{\partial^{2} \overline{w}}}{{\partial \varsigma^{2} }} = 0. \\ \end{aligned}$$
(53)

The corresponding boundary conditions for the simply supported axisymmetric circular plate are

$${\text{At}}\,\xi = {1}:\overline{w}(\xi ) = 0,\overline{S}_{w1} (\xi ) = 0,\overline{S}_{w2} (\xi ) = 0.$$
(54)

The dimensionless deflection can be assumed as

$$\overline{w} = T(\varsigma )(1 + A_{1} \xi^{2} + A_{2} \xi^{4} + A_{3} \xi^{6} ),$$
(55)

where the coefficients A1, A2 and A3 can be determined by substituting Eq. (55) into the boundary conditions Eq. (54). Applying the Galerkin method yields

$$\begin{aligned} & \int_{0}^{1} {\left[ {\frac{{b_{3} }}{6}\left( {\frac{{\partial^{6} \overline{w}}}{{\partial \xi^{6} }} + 3\frac{{\partial^{5} \overline{w}}}{{\xi \partial \xi^{5} }} - 3\frac{{\partial^{4} \overline{w}}}{{\xi^{2} \partial \xi^{4} }} + 6\frac{{\partial^{3} \overline{w}}}{{\xi^{3} \partial \xi^{3} }} - 9\frac{{\partial^{2} \overline{w}}}{{\xi^{4} \partial \xi^{2} }} + 9\frac{{\partial \overline{w}}}{{\xi^{5} \partial \xi }}} \right) - b_{4} \left( {\frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + 2\frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} - \frac{{\partial^{2} \overline{w}}}{{\xi^{2} \partial \xi^{2} }} + \frac{{\partial \overline{w}}}{{\xi^{3} \partial \xi }}} \right)} \right.} \\ & \quad + \left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \left( {3\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }} + \frac{{\partial \overline{w}}}{\xi \partial \xi }} \right) - 4b_{5} \left( {\frac{{\partial \overline{w}}}{\xi \partial \xi }} \right)^{2} \left( {\frac{{\partial \overline{w}}}{\xi \partial \xi } - 3\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right) \\ & \quad \left. { - {2}b_{3} \left[ {3\frac{{\partial \overline{w}}}{\xi \partial \xi }\left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{2} + 2\left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \frac{{\partial^{3} \overline{w}}}{{\xi \partial \xi^{3} }} + \left( {\frac{{\partial \overline{w}}}{\partial \xi }} \right)^{2} \frac{{\partial^{4} \overline{w}}}{{\partial \xi^{4} }} + \left( {\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}} \right)^{3} + 4\frac{{\partial \overline{w}}}{\partial \xi }\frac{{\partial^{2} \overline{w}}}{{\partial \xi^{2} }}\frac{{\partial^{3} \overline{w}}}{{\partial \xi^{3} }}} \right] - \frac{1}{{\vartheta^{2} }}\frac{{\partial^{2} \overline{w}}}{{\partial \varsigma^{2} }}} \right]\overline{w}\xi {\text{d}}\xi = 0. \\ \end{aligned}$$
(56)

By substituting the dimensionless deflection Eq. (55) into Eq. (56), the vibration differential equation can be derived as

$$\frac{{d^{2} T}}{{d\varsigma^{2} }} + \frac{{J_{1} }}{{J_{0} }}T + \frac{{J_{2} }}{{J_{0} }}T^{3} = 0$$
(57)

in which the coefficients J0, J1, J2 are

$$\begin{aligned} J_{0} & = \frac{1}{{\vartheta^{2} }}\int_{0}^{1} {(1 + A_{1} \xi^{2} + A_{2} \xi^{4} + A_{3} \xi^{6} )^{2} \xi d\xi } \\ J_{1} & = 64\int_{0}^{1} {(b_{4} A_{2} - 6b_{3} A_{3} + 9b_{4} A_{3} \xi^{2} )(1 + A_{1} \xi^{2} + A_{2} \xi^{4} + A_{3} \xi^{6} )\xi d\xi } \\ J_{2} & = \int_{0}^{1} {\eta (1 + A_{1} \xi^{2} + A_{2} \xi^{4} + A_{3} \xi^{6} )\xi d\xi } \\ \eta & = {16}b_{3} [(A_{1} + 6A_{2} \xi^{2} + 15A_{3} \xi^{4} )^{3} + 24\xi^{2} (A_{1} + 2A_{2} \xi^{2} + 3A_{3} \xi^{4} )^{2} (A_{2} + 10A_{3} \xi^{2} ) \\ & \quad + 3(A_{1} + 22A_{2} \xi^{2} + 95A_{3} \xi^{4} )(A_{1} + 2A_{2} \xi^{2} + 3A_{3} \xi^{4} )(A_{1} + 6A_{2} \xi^{2} + 15A_{3} \xi^{4} )] \\ & \quad - 32(A_{1} + 2A_{2} \xi^{2} + 3A_{3} \xi^{4} )^{2} [\xi^{2} (A_{1} + 5A_{2} \xi^{2} + 12A_{3} \xi^{4} ) + 2b_{5} (A_{1} + 8A_{2} \xi^{2} + 21A_{3} \xi^{4} )]. \\ \end{aligned}$$
(58)

Eq. (57) is the Duffing equation. By defining

$$T = \kappa \overline{T},\,\,\varpi_{0}^{2} = \frac{{J_{1} }}{{J_{0} }},\,\,\varepsilon = \frac{{J_{2} }}{{J_{1} }}\kappa^{2}$$
(59)

with κ and ε representing the small parameters, the Duffing equation can be written as

$$\frac{{d^{2} \overline{T}}}{{d\varsigma^{2} }} + \varpi_{0}^{2} (\overline{T} + \varepsilon \overline{T}^{3} ) = 0.$$
(60)

On the basis of the initial condition

$$\overline{T}(0) = \overline{B},\,\,\frac{{d\overline{T}}}{d\varsigma }|_{\varsigma = 0} = 0,$$
(61)

where \(\overline{B} = B/\kappa\) and B denotes the amplitude, the Duffing equation Eq. (60) can be solved according to the Lindstedt–Poincaré Method45. The second order approximate solution is written as

$$\overline{T} = \overline{B}\cos (\varpi \varsigma ) - \frac{{\varepsilon \overline{B}^{3} }}{32}[\cos (\varpi \varsigma ) - \cos (3\varpi \varsigma )] + \frac{{\varepsilon^{2} \overline{B}^{5} }}{1024}[23\cos (\varpi \varsigma ) - 24\cos (3\varpi \varsigma ) + \cos (5\varpi \varsigma )],$$
(62)

where the nonlinear vibration frequency is given by

$$\varpi^{2} = \varpi_{0}^{2} \left( {1 + \frac{{3\varepsilon \overline{B}^{2} }}{4} - \frac{{3\varepsilon^{2} \overline{B}^{4} }}{128}} \right).$$
(63)

Finally, substituting Eqs. (59), (62), (63) into Eq. (55), the nonlinear free vibration problem of axisymmetric flexoelectric circular plate can be solved. In addition, the dimensionless natural frequency \(\varpi\) is related to the natural frequency by

$$\varpi = \omega \sqrt {\frac{{\rho R^{2} }}{{c_{4} - d_{1} }}} .$$
(64)

From Eq. (63), the influence of amplitude on dimensionless natural frequency in different material length scale parameters is shown in Fig. 7. It can be found from Fig. 7 that the dimensionless natural frequency increases with the increase of amplitude. The dimensionless natural frequency with l0 = l1 = l2 ≠ 0 (including all strain gradient stiffening effect) is almost 4 times of that with l0 = l1 = l2 = 0 (ignoring all the strain gradient stiffening effect). This demonstrates the stiffening effect of strain gradient is remarkable, which is consistent with that obtained from Fig. 5. In addition, the strain gradient spherical component (l0 ≠ 0) dominates the stiffening effect, while the symmetric rotation strain gradient component (l2 ≠ 0) exhibits the least stiffening effect.

Figure 7
figure 7

The influence of amplitude on dimensionless natural frequency.

Full size image

Conclusion

In this paper, the nonlinear flexoelectric model for circular plate in large deflection deformation is established based on the flexoelectric theory. The current model will reduce to the corresponding linear model when terms associated with nonlinearity are neglected.

In order to solve the nonlinear bending equations, DQM is introduced and the validity of DQM is verified by the theoretical results of linear bending. The results demonstrate that the static bending deflection induced by the inverse flexoelectric effect is small and opposite in comparison with that generated by transverse load q. The final deflection is a superposition of these two parts. Although the inverse flexoelectric effect is weak, it strengthens as the thickness of plate decreases, which can be further enhanced when the plate thickness reaches nanometer scale. Moreover, the electric potential can be significantly affected by the transverse load q. The larger the load, the more uneven the potential distribution will be, since the bending deformation of circular plate under transverse load q can induce polarization and electric potential by direct flexoelectric effect.

Moreover, the nonlinear free vibration of simply supported axisymmetric flexoelectric circular plate is also investigated by combining the Galerkin method and Lindstedt–Poincaré Method. The dimensionless natural frequency increases with the increase of amplitude. When the thickness of circular plate is close to the material length scale parameter, the stiffening effect of strain gradient (mainly the strain gradient spherical component) dominates the bending rigidity compared with the traditional bending rigidity.