Abstract
We have investigated proton acceleration in the forward direction from a near-critical density hydrogen gas jet target irradiated by a high intensity (1018 W/cm2), short-pulse (5 ps) laser with wavelength of 1.054 μm. We observed the signature of the Collisionless Shock Acceleration mechanism, namely quasi-monoenergetic proton beams with small divergence in addition to the more commonly observed electron-sheath driven proton acceleration. The proton energies we obtained were modest (~MeV), but prospects for improvement are offered through further tailoring the gas jet density profile. Also, we observed that this mechanism is very robust in producing those beams and thus can be considered as a future candidate in laser-driven ion sources driven by the upcoming next generation of multi-PW near-infrared lasers.
Similar content being viewed by others
Introduction
Over the past decade, laser-accelerated ion beams1,2,3,4 have attracted considerable interest due to their unique characteristics and have already enabled many applications. These include ultrafast radiography5,6,7,8, and prompt heating of dense matter9,10,11. However, other scientific (laser-driven ion fusion)12, medical (hadron therapy)13,14,15, or more main-stream (like nuclear fuel recycling through Accelerator-Driven-System) applications can only be unlocked with further improvement of the proton beam in terms of flux and maximum energy. Common to all these applications is indeed the need for an ion beam with controllable energy bandwidth, low divergence at the source, and also high repetition rate. The hurdle of a high repetition ion beam can be addressed easily with the increasing repetition rate of presently available16 and upcoming17,18, laser drivers. Lifting the other two hurdles of bandwidth and divergence is however more difficult as it requires moving away from the most relied upon acceleration method, i.e. the so-called Target Normal Sheath Acceleration (TNSA) mechanism19. This mechanism is very robust, but it intrinsically produces broadband energy (with 100% spread, unless the number of available ions to accelerate is purposely reduced20) beams having angular divergence21,22.
Several alternative ion acceleration schemes that would offer the desired improvements in beam parameters have been already proposed and are currently being tested. A first scheme relies on radiation-pressure driven acceleration (RPA) of ions in ultra-thin targets23. It is rather demanding not only in terms of target thickness, but also in terms of laser parameters. Indeed, for RPA the laser pulse must have ultra-high temporal contrast to not damage the target prior to the main pulse irradiation24. The laser pulse must also have ultra-high intensity such that this acceleration mechanism would be dominant with respect to TNSA. For these reasons, with present-day lasers, only the onset of the RPA acceleration mechanism, mixed with TNSA, could be demonstrated25,26,27, and questions related to the beam quality, namely problems with triggering beam instabilities28 still remain.
A second scheme also relies on the laser radiation pressure, but this time in thicker targets where it directly puts in motion the ions at the critical density interface at which the laser is stopped. This is the so-called hole-boring (HB) mechanism29 that accelerates these front-surface ions30.
In a partially expanded target having near-critical density31,32, a third ion acceleration mechanism can take place, it is the so-called Magnetic Vortex Acceleration mechanism (MVA). As laser light can propagate into an expanded target, fast electron currents generated near the target rear surface form a long-living quasistatic magnetic field. This field generates an inductive electric field at the rear plasma-vacuum interface that complements TNSA in providing ion acceleration33,34,35.
Finally, a fourth ion acceleration mechanism was introduced by Denavit et al.36, followed by Silva et al.37 for critically dense targets. It is known as the Collisional Shock Acceleration (CSA) mechanism. It is based on the fact that the laser pulse can induce a collisionless shock wave in a near-critical density target, and the propagating shock can reflect ions in the target and accelerate them to high energies. Such shock wave is generated by the laser-accelerated fast electrons injected into the target. It is collisionless since its dissipation mechanism is due to the electrostatic losses. Due to their high energy, the collisional dissipation into these electrons is negligible38, however collisionless processes (i.e. mediated by instabilities and plasma waves) can provide enough energy dissipation39. Thus, a density steepening (shock) can form as the fast electrons overcome the target medium in their propagation37.
Several numerical studies have been performed to optimize the target and laser parameters for CSA, and have shown that targets with peak densities close to the critical density with smooth gradients40,41, represent optimal conditions. CSA was then extended to under-critical density targets by d’Humières et al.41. There, the shock wave is not created by the laser, but ions-driven in a downward density gradient. This low density CSA (LDCSA) scheme was demonstrated experimentally42,43, to produce low divergence, yet broadband beams since sheath acceleration in the rear end of the target density profile provides additional acceleration.
Laser-driven CSA protons have significant advantages other than the prospects of low divergence and monoenergetic beams. First, the scaling with the laser energy of CSA is more favorable than that of TNSA, namely, the ion energy scales linearly with laser intensity44, whereas for TNSA it scales with the square root of the laser intensity45. The second point is purely practical since with TNSA or RPA, the solid targets that are used require precise target alignment for each shot, need strict laser temporal contrast, and produce debris in the target chamber. With CSA, especially using gas jets as targets, operation would significantly be easier at upcoming high-repetition rate laser facilities, eliminating the need for target replacement and realignment. Moreover, using a lower-than-solid density for the target would reduce the amount of debris generated46. We note that continuous operation of gas jets in high-vacuum chambers have been shown to be possible47, hence eliminating this concern.
The CSA scheme has been clearly demonstrated experimentally using CO2 lasers48. Indeed, the long wavelength (10.6 µm) of these lasers allows for controlled near-critical targets to be easily produced. As mentioned above, the laser-driven CSA mechanism is most efficient in a critically dense plasma where n e ≥ γn cr 49, with ncr = ε o m e ω laser 2/e 2 where ω laser is the angular frequency of the laser, and \(\gamma =\sqrt{1+{a}_{0}^{2}}\) is the relativistic factor for the electrons derived from one-dimensional energy and momentum flux conservation, with \({a}_{0}={({I}_{L}{\lambda }_{L}^{2}/1.37\times {10}^{18}{\rm{W}}.\mu {m}^{2}{{\rm{.cm}}}^{-2})}^{1/2}\) the normalized laser vector potential, I L and λ L being, respectively, the laser intensity and wavelength. In practical units, n cr [cm−3] = 1.1 × 10 21/λ L 2[µm]. Since the wavelength of CO2 lasers is 10.6 μm, the minimum required target density to be overcritical in these conditions is 1 × 1019 cm−3, which is easily created with commercially available gas bottles and a pulsed valve50. Using these targets with high intensity lasers, it was shown that CSA could indeed generate monoenergetic proton beams, i.e. having less than 5% energy bandwidth, of low (<100 mrad) divergence. The major downside is that in practice CO2 lasers are limited to irradiances \({I}_{L}{\lambda }_{L}^{2}\) around 1019 W.µm2/cm2.
Near-infrared (0.8–1 µm wavelength) lasers exist already at higher irradiances when compared to CO2 lasers, with \({I}_{L}{\lambda }_{L}^{2}\) reaching already more than 1021 W.µm2/cm2 in several facilities world-wide, with prospects for currently built facilities to reach I > 1023 W/cm2 51. However, the difficulty there with respect to CSA is that higher density targets are required, i.e. with densities above 1021 cm−3 (n cr for a 1 µm wavelength laser). This is already possible to achieve with foams52; it becomes nowadays possible with gas jets53,54.
In this article we will show that using a Hydrogen gas jet with a peak density of 2.7 n cr , which is irradiated by an intense, short-pulse laser having a wavelength of 1.054 µm, proton beams that display the characteristics of CSA-accelerated beams were observed. With good consistency, the beam displays a quasi-monoenergetic peak up to 1 MeV with a very low angular divergence. The energy of the peak is observed to correlate well with the laser intensity and the target density. The outline of the article is as follows. We will first describe our experimental setup and the measured results. Next, we will present hydrodynamic simulations that bring insight into the target conditions, notably suggesting that the target width was affected by the prepulse accompanying the intense laser pulse. We will also present results of particle-in-cell (PIC) simulations of the interaction, which reveal that HB and CSA are both at play, but where CSA, in the conditions of the experiment, produces higher energy ions (here protons) than HB acceleration. Moreover, the energy of the ions generated by CSA is found to be in reasonable agreement with the measured ones. Finally, we will discuss prospects for future improvement of such acceleration technique, still with near-infrared lasers, using tailored gas jets as targets. We note that the recent result of Helle et al.55 exploits as well a high density hydrogen gas jet and a near-infrared (800 nm wavelength) laser for directed proton acceleration. There, the density is increased by the generation of hydrodynamic shocks induced by auxiliary laser beams and the acceleration is induced by a magnetic vortex. This differs from our results which, when obtained at higher plasma densities, i.e. >2 ncr, are rather related to CSA, as suggested by our simulations.
Experimental Setup
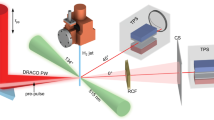
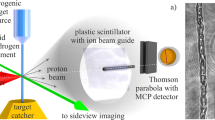
The experiment was performed using the Titan laser at the Jupiter Laser Facility (LLNL, USA), using the experimental setup shown in Fig. 1. The short pulse laser arm of Titan, focused with an F/3 off-axis parabola, irradiated a high density gas jet with a maximum of 210 J in 5 ps with a wavelength of 1.054 μm. The laser had a best focus of 10 µm (at its full width at half maximum, or FWHM), containing an encircled energy of around 35%, thus giving a peak intensity at best focus of \({I}_{L}{\lambda }_{L}^{2}\) = 2.2 × 1019 W.µm2/cm2, i.e. yielding the parameter a0 = 4.2. With these parameters, γn cr = 4.3 × 1021 1/cm3, which a priori sets a very high density requirement to efficiently drive CSA.
Proton spectrometers were placed, as indicated in Fig. 1, on the horizontal plane to measure the proton beam energy and angular distribution. Since we used a pure Hydrogen gas (H2), the spectrometers were not equipped in a Thomson parabola configuration, i.e. they use a simple magnetic deflection to resolve the proton energies. This allows also to use at the spectrometer entrance a wide slit (horizontally) to resolve, for each spectrometer, the proton beam over ±100 mrad around its mean angle of observation. In Fig. 1 is shown only the spectrometer located at 0° with respect to the laser incident axis. Other spectrometers were located at 21°, 43°, and 92° with respect to the same axis. As detectors, we used absolutely calibrated56 FujiFilm image plates of type TR.
The nozzle that we used for the gas jet is a Laval type design to achieve supersonic gas outlet velocity50. The orifice was rectangular: 1 mm wide and 300 μm long with a throat of 300 × 300 µm2 located 3 mm below the opening. Before the experiment, we performed 3D optical (using a He-Ne, 633 nm wavelength laser probe) tomography measurements to characterize the rectangular gas profile in the output of the nozzle using Argon gas. It should be noted that the difference in gas flow found by our measurement and others57 between Argon, a monoatomic gas that was used in the test, and Hydrogen (H2), a diatomic gas, has a difference of profile and molecular density of less than 1%. This is consistent with calculations that can be made of the gas flow in the exit of the nozzle58, which suggest that the differences between Ar and H2 flows (having respective specific heat ratio 7/5 for for H2, and 5/3 for Ar) are minor. Figure 2 shows a horizontal cross-section of the measured gas density distribution at 500 μm above the base of the nozzle. We measured, in the range of 10 to 100 bars, that the backing pressure is linearly related to the peak density of the gas jet, which is consistent with other measurements50,59,60. Density profile measurements at higher pressure are difficult, because the high-density in the jet induces first refraction of the optical probe and even, for very high pressures, fully prevents the probe to penetrate the gas jet.
3-D tomography of the gas jet. (a) The horizontal cross-section of the gas jet at 500 μm above the nozzle. The colorscale units are in molecular density (molecule/cm3/bar). (b) Vertical and horizontal lineouts of the image in (a), which show that the form of the gas jet can be represented as a quasi-perfect Gaussian.
As shown schematically in Fig. 1, the laser was focused at the rising edge of the Hydrogen gas jet and along the narrow part of the density profile (see Fig. 2a). Since the density profile is Gaussian, we chose a position in this profile for the location of the best focus of the laser, which was placed at 150 μm in front of the location of the peak density. The height of the laser focus was 500 μm above the gas jet nozzle, i.e. corresponding to the density profiles shown in Fig. 2b.
To produce the high backing pressures needed to obtain near-critical densities in the gas jet, we start from a commercially available gas canister (pressurized at 100 bars); then we used a Haskel (www.haskel.com) pneumatic gas compressor able to compress the gas to 1000 bars, a Clark Cooper EX40 electro-valve (www.clarkcooper.com) that is rated for these high pressures, and high pressure pipes and fittings from Swagelok (www.swagelok.com). The gas that we used was Hydrogen (H2), which is a diatomic molecule at room temperature; once ionized by the laser, the peak ion density during the interaction is double the molecular density that is shown in the measurements of Fig. 2. Therefore, by extrapolating our measurements to backing pressures between 150 bars to 900 bars of gas, we conclude that we can a priori vary the ionized electron density up to 2.7n cr .
Experimental Results
Before presenting the proton acceleration results, we should note that the laser pulse that we used to drive the ion acceleration had a pedestal before the main pulse arrives. This pedestal, or prepulse, as measured during the experiment with fast diodes and a water-switch cell, contains around 20 mJ of energy (at the target chamber center (TCC), i.e. at the location of the short-pulse focus) and is characterized by a short ramp (~0.3 ns) preceding a ~1 ns flat plateau. The calibration of the measurement was made by sending a low-energy, 3 ns duration pulse through the amplifier chain and the compressor, and measuring its energy simultaneously at TCC, and on the diode which measures the prepulse on every shot. Note that these prepulse values are similar to the ones measured in other runs at the same laser facility by other groups61,62. Since the prepulse intensity (\({I}_{L}{\lambda }_{L}^{2}=\) 1013 W.µm2/cm2) is above the ionization threshold, it modified significantly the gas jet density profile ahead of the main pulse irradiation. This was on one hand beneficial, since it reduced the thickness of the gas target, which increases the efficiency for CSA, but on the other hand, it had the detrimental effect to push the critical density interface away, i.e. this effectively defocuses the high-intensity laser pulse arriving on the target interface and thus reduces its ability to drive a strong shock.
The modification of the gas target profile induced by the laser prepulse is determined by hydrodynamic simulations of the gas jet evolution when it is irradiated by the prepulse. Here we relied on hydrodynamic simulations, to infer the target density profiles at the time of the short-pulse irradiation. Indeed, we could not optically probe the interaction due to the overdense gas jet and would have needed an x-ray source (or a second short pulse to create an x-ray burst) to radiograph the gas or plasma. Nevertheless, hydrodynamic simulations in these conditions are well-benchmarked and are able to grasp quantitatively the plasma evolution; such procedure of relying on hydrodynamic simulations has indeed been validated quantitatively many times over the years, as shown e.g. in refs42,63,64,65,66. For such simulations, we used the FCI2 hydrodynamic code67 in 2D, modelling the same xy plane as shown in Fig. 2a. Fitting the measurements shown in Fig. 2, the profile of the gas jet used in the simulation was a Gaussian, as mentioned in the previous section, with a FWHM of 400 µm and using fully ionized Hydrogen with a temperature of 300 K. In the hydrodynamic simulations, the laser propagation from the near field (the focusing optics) to the far-field (focus) and after, is described by a 3D ray-tracing package68. We specify a power law that fits the experimental laser power of the pre-pulse in order to get the right laser energy. At each time step, the power is distributed over the rays, then each ray propagates inside the plasma and deposits its power via inverse Bremsstrahlung. Then, a non-local electron transport model is used for modeling heat fluxes. The focal plane is adequately defined in terms of spatial dimensions, but ray-tracing packages (based on geometrical optics) do not take into account diffraction. This modelling67 is sufficient in many situations for describing plasma heating and is widely used in radiative-hydrodynamics ICF codes that have been well benchmarked69,70.
In our simulations, the box used was 1.2-mm long and 400-microns wide, we set the initial density profile that fits the gas-jet’s longitudinal profile (as derived from Fig. 2 of the paper), and the initial temperature was set to an arbitrary low temperature. FCI2 being a radiative-hydrodynamics code designed for describing plasma heating and dynamics, the lower temperature bound used for calculating ionization is around 1 eV, leading to a fully ionized plasma in the whole simulation box, even far from the focal spot. But, this has no implications on the fact that plasma heating is localized and on the formation of a blast wave: the plasma is still cold far from the focal spot.
The results of the prepulse irradiation of the gas jet are shown in Fig. 3 at various times after the prepulse had begun. We observe that it significantly modified the gas jet profile, reducing it to about half its initial thickness after 1 ns. As a consequence, the main laser pulse will encounter the remaining steep and dense gas jet interface while being defocused by ~150 µm. Since the focusing optics of the laser is F/3, the effect of this defocusing results in a reduced intensity at this location of around 3 × 1018 W/cm2, a 0~1. This is estimated by analyzing a set of images of the short-pulse beam, as focused by the F/3 parabola, taken at various positions around the best focus. The defocusing is seen to follow very well the theoretical estimate for a Gaussian beam, and we observe that a defocus of 150 µm corresponds to a nominal increase of the beam FWHM from 10 µm (at best focus) to ~45 µm. Apart from such peak laser intensity condition, we also varied (reduced) during the experiment the laser energy or moved the laser focusing point further to the foot of the gas density profile, hence further reducing the laser intensity on the critical density interface. These various conditions will be summarized below.
Experimentally, we first performed a series of shots using the setup shown in Fig. 1. While keeping the laser intensity constant, we varied the backing pressure in the gas jet from 170 to 900 bars, which is equivalent to varying the peak electron density in the ionized target gas jet from 0.5n cr to 2.7n cr . The resulting proton spectra measured with the spectrometer oriented at 0° are shown in Fig. 4. Note that the 100 keV lower end of the spectrum is the instrumental lower detection limit.
A comparison of experimentally measured proton beams generated from the gas jet target in the forward (0°) direction and with different peak density for the gas jet target. (a) Proton spectra measured at 0°. Note that the spectra shown here have not been spectrally deconvolved by the width of the spectrometer slit. The latter is however small compared to the width of the spectral peaks. For example, the spectral peak measured at 2.5ncr, which has a width of ΔE/E ~0.16 would have this width reduced to 0.13 by deconvolving the slit width. Similarly, the spectral peak measured at 1.4ncr, which has a width of ΔE/E ~0.3 would have this width reduced to 0.26 by deconvolving the slit width. (b) Divergence of the proton beam as measured continuously along the slit of the spectrometer located at 0°, and at the location of the proton spectral peak that can be observed in (a). Note that outside the central axis (0°), the spectrum has also a similar shape as shown in (a), with a spectral peak around the same value as at 0°, but with much lower proton number.
As seen in Fig. 4, as the density of the gas target was varied from underdense to overdense, the proton spectrum clearly shows that the energy of the peak in the spectrum increased with the target gas density. Also shown in Fig. 4 are the angular patterns of these proton beams, all displaying a narrow distribution and well resolved within the acceptance of the single spectrometer located at 0°. We stress that in all cases, no signal was recorded in the other spectrometers located at larger angles around the chamber (i.e. there was no signal above the noise level). In the case of overcritical densities, due to the simultaneous observations of a peak in the spectrum, and of a narrow angular distribution for the accelerated beam, we conjecture that the dominant acceleration mechanism could be CSA, as in the case of the CO2 laser experiments. As will be detailed below, we find that this scenario is supported by the numerical simulations.
A clear spectral peak could not be distinguished in the case of the peak density of 0.5n cr , although the angular pattern of the beam in this case displayed a narrow profile, even narrower than for higher gas densities: the divergence of this beam is 13 mrad. This extremely small divergence could be due to the MVA mechanism discussed above, i.e. to a quasi-static magnetic field on the back side of the target formed by the hot electrons accelerated directly by the laser on the front side and by the resulting return current33. We note that experimentally, proton beams with small divergence have also been observed before by Willingale et al.71 from underdense gas targets accelerated by the TNSA/MVA process.
As the density of the target is increased to 1.4n cr , the spectrum however clearly changes with a significant peak in the proton beam spectrum appearing at 0.4 MeV (with ΔE/E ~0.3). This appears to be a combination of acceleration mechanisms where there is a quasi-monoenergetic beam on top of what appears to be TNSA accelerated protons at lower energy. When the density of the gas jet target is further increased to 2.5n cr , the peak has shifted to several hundred keV higher in energy (with ΔE/E ~0.16).
Assuming a similar proton beam divergence in the horizontal and vertical directions, we can estimate the proton number in the spectral peaks observed in Fig. 4a: using the angular width observed in Fig. 4b, both for the spectral peak measured for the plasma density 2.5 ncr, and the one measured for the plasma density 1.4 ncr, we obtain ~109 protons contained in the peak. This is equivalent, at these proton energies, to ~0.1 mJ of energy carried by the spectrally peaked protons.
The energy that the protons can acquire through CSA, HB, and TNSA can be estimated using analytical expressions presented by Wilks et al.29, Fiuza et al.44 and Stockem-Novo et al.72. For these theoretical studies, the final accelerated proton energy, i.e. acquired as the ions are reflected off the shock37 or accelerated by the hole-boring potential, can be expressed in terms of \(\sqrt{I/{n}_{i}}\). For the energy of the ions accelerated by HB, we use mi(vhb)2/2, where mi is the ion mass and vhb is the HB ion velocity as expressed in ref.29, i.e. \({v}_{hb}=c\sqrt{{m}_{e}{n}_{cr}I{\lambda }^{2}/2{m}_{i}{n}_{i}1.37\times {10}^{18}}\), where λ is in microns and I in W/cm2. Using a number of shots recorded during the experiment with various laser intensities and gas jet densities, the energy of the quasi-monoenergetic proton beam is plotted against the experimental inputs in the expression \(\sqrt{I/{n}_{i}}\) in Fig. 5a. The parameter space that we could explore during the experiment was limited due to the low number of shots allocated for the campaign. This low shot number and variability in the laser parameters affects our ability to demonstrate reproducibility. Nonetheless, we can state that, with the limited shots we could get on Titan, the robustness of the process generating peaked spectral distribution at high densities was good as witnessed by the spectra shown in Figs 4 and 5.
(a) The proton energy of the quasi-monoenergetic peak recorded in the spectrum for various shots (red dots, as measured in the experiment) for different values of the parameter (I/ni)1/2 and as compared to the hole-boring model (Wilks et al.29) and two CSA models (Fiuza et al.44 & Stockem-Novo et al.72). The red center point indicates the energy of the largest population (spectral peak) of protons. The horizontal error bar corresponds to the FWHM of the signal around the spectral peak that is observed. (b) A typical spectrum corresponding to the points encircled in yellow in (a), which correspond to shots recorded at lower pressures, and which are observed to fall near the curve for the hole-boring model. (c) A typical spectrum of the other data points, recorded at higher pressures, which are closer to the CSA scalings.
The curve of green dots in Fig. 5a, represents the expression presented by Fiuza et al.44 where this expression is dependent on the velocity of the electrostatic shock created by the hot electrons. The shock velocity is there v sh,F = (2Mc s )/(1 + M 2 c s 2/c 2) where c s is the upstream sound speed, c is the speed of light and M ~ \(\sqrt{(1+\eta )/0.4}{({n}_{{cr}}/{n}_{i})}^{1/2}{{a}_{0}}^{1/2}\) 37 is the shock Mach number. For our experimental intensities, we took η to be 0.273, which is the absorption efficiency at the critical density surface at the (defocused) laser intensity we used. The blue curve in Fig. 5a represents the expression presented in Stockem-Novo et al.70 where their expression is based on the velocity of the adiabatic expansion of a gas; this model looks at a shock driven 3D spherical expansion, i.e. it should lead to an underestimate of what we obtain since we work more in a condition closer to a planar shock driven in the gas jet by the high-intensity laser. Here, the velocity is \({v}_{sh,SN}=c\sqrt{Z{m}_{e}{n}_{cr}{{a}_{0}}^{2}/8{m}_{i}{n}_{0}}(1+{K}_{ad})\) where K ad = 7/3 for diatomic molecules.
As shown in Fig. 5a, we can observe that the experimental data fall either close to the curve corresponding to HB or to the ones corresponding to CSA. We indeed observed that the data points encircled in the yellow line, close to the HB scaling, have a typical spectrum shown in Fig. 5(b) where, on top of an exponentially falling spectrum, there are one or more small peaks on a plateau. These data points correspond to shots at a lower density of the gas jet (i.e. close to ncr), hence they are higher in the curve because the gas density (ni) is lower. In contrast, the other experimental points with a typical spectrum with a strongly pronounced spectral peak as found in Fig. 4a and also shown in Fig. 5c, follow the curves describing CSA. These points have been obtained at higher gas densities (i.e. >2 ncr), since they correspond to lower positions in the graph as the factor (I/ni)1/2 is smaller. In short, the protons accelerated at high densities, and which display a strong spectral peak, have higher energy than what is predicted by the hole-boring acceleration mechanism and are closer to the CSA trends.
Numerical Simulations
To verify that CSA is indeed the proton acceleration mechanism inducing the strong spectral peaks observed in our experimental conditions at high densities (see Figs 4a and 5c) and to gain insight into the actual acceleration processes, we performed particle-in-cell (PIC) simulations using the code OSIRIS74 in 2D. The simulation box was 1273 μm long and 16 μm wide, resolved with 48000 × 600 cells and 8 particles per cell. The total simulation time was 20 ps, sampled with a time step of Δt = 0.06 fs. The initial plasma profile, with peak density of 2.7n cr , was used for the first set of simulations, as shown (in blue) in Fig. 6, and which corresponds to the modified gas jet target profile as found by the hydrodynamic simulations shown in Fig. 3 for the 1 ns duration irradiation of the gas jet by the prepulse. The simulation box is transversely periodic, and the laser is launched from the left-hand wall. The laser is transversely a plane wave, with a temporal envelope of 5 ps at FWHM. The maximum laser intensity reaches the center of the gas jet (x = 0) at t = 6.5 ps from the beginning of the simulation.
(a) The density profiles of the gas jet as calculated by FCI2 (see Fig. 3) and used as the input into the PIC simulation. Longitudinal density profiles of the gas jet along the laser axis for two durations of pre-pulse irradiation preceding the main laser pulse (the unperturbed density profile is shown in black). The blue profile corresponds to conditions explored in the present experiment. The red profile corresponds to longer prepulse irradiation that would lead to a shorter density profile. (b) Plasma profiles at t = 5.7 ps (0.8 ps before the peak of the main pulse reaches x = 0 mm). Both profiles are obtained for an irradiation by a laser pulse having an intensity characterized by a0 = 4.
In general, we note that due to the quasi-1D geometry employed in the simulations, we can expect that the proton energies will be overestimated, especially in the case of TNSA protons75. We underline that multi-dimensional simulations of this setup are beyond the current computational capabilities. However, even if one would be able to perform a full-scale 3D simulation of the interaction, it would not be possible to guarantee the quantitative agreement in the proton energies between the PIC simulations and experiment, because this result is sensitive to the differences in the thickness of the initial plasma profile. An additional difficulty rises from the fact that the peak plasma density of the gas jet is close to the relativistic critical density, and small variations in the laser intensity might change the longitudinal position of the critical density interface. Nonetheless, as will be detailed below, the picture described by the simulations is found in reasonable agreement with the experimental data, hence allowing us to believe that the physics observed in the simulations is adequate, and thus emphasizing that shock acceleration as the main acceleration mechanism.
We have tested in the simulation irradiating the gas jet at two laser intensities, namely a 0 = 1 and a 0 = 4. We chose these two intensities as they correspond to the maximum intensity case (a 0 = 4, i.e. in the plane of best focus of the laser), or the case of reduced intensity (a 0 = 1, resulting from the laser defocus by 150 µm due to the gas jet deformation induced by the prepulse). In both cases, a clear shock structure had formed at the target critical density interface irradiated by the laser. The resulting phase space of the accelerated protons for our experimental conditions is illustrated for the two laser intensities in Fig. 7b and d. We observed that for both laser intensities, the phase space exhibits TNSA accelerated protons, those from hole-boring, as well as CSA accelerated ones which corroborates the fact that we observe several energy distributions, namely several peaks and continuous spectrum. The higher energy CSA accelerated protons led to, as shown in Fig. 7a and c, peaks in the spectrum. Here, the TNSA accelerated proton spectrum is not included to highlight the population accelerated by CSA, and its correspondence to the experimentally observed spectral peak corresponding to a peak density of 2.5 n cr , which is shown (red curve) in Fig. 4a. In the first case the peak is close to 1 MeV, i.e. consistent with the red curve measurement shown in Fig. 4a, which supports our conjecture of the laser beam being indeed defocused to such a reduced intensity. This is further supported by the fact that the energy of the protons in the simulation using a 0 = 4 is higher than the one recorded in the experiment.
Simulated proton properties obtained with the blue plasma profile shown in Fig. 6 at t = 11.7 ps. (a) Spectrum of the shock accelerated protons using a laser intensity of a0 = 1. (b) Corresponding proton longitudinal phase space with a laser intensity of a0 = 1. (c) Spectrum of the shock accelerated protons using a laser intensity of a0 = 4. (d) Corresponding proton longitudinal phase space with a laser intensity of a0 = 4.
Figure 8 shows the temporal evolution of the electron density and allows us to read directly the velocity of the density discontinuities in units of c, the speed of light. This is done for the two cases of the two density profiles of the gas jet shown in Fig. 6 of the paper as modified by the ASE of the Titan short-pulse laser (having a 0 = 1 in both cases). The interaction with the laser prompts a partial expansion backwards of the initially underdense sections of the plasma profiles. One observes that one cannot therefore clearly define a single acceleration velocity from Fig. 8, because of the density gradients in the system. However, there are several density discontinuities that propagate into the gas jet. The white line highlights the dominant one (corresponding ion phase spaces are shown in Figs 7b and 9a). The velocity of the maximum density peak in Fig. 8a is v = 0.017c. If we assume the ions reflected from this peak would have the velocity v i = 2 v, the ion energy is ~0.54 MeV. The velocity in Fig. 8b is somewhat higher, v = 0.024c, so the reflected ions are expected to be around 1 MeV. We note that these values are consistent with the spectrum of the reflected ions shown in Figs 7a and 9c and which correspond to the conditions in which these simulations were run (i.e. to a gas density of 2.5 n cr ).
Electron density evolution as a function of time extracted from the PIC simulations. Here, the time is normalized to the laser frequency ω0, and the propagation length c/ω0, where c is the speed of light. The initial density profiles correspond, respectively, to the (a) blue, and (b) red profiles shown in Fig. 6. The laser normalized intensity is a0 = 1 in both cases. The white dashed lines show the hole-boring velocity, and full lines the corresponding shock velocity.
Proton properties obtained, for two different laser intensities (as labeled), with the plasma profile corresponding to the red profile shown in Fig. 6 (i.e. corresponding to a 1.9 ns prepulse) at t = 11.7 ps. (a,b) Proton longitudinal phase space. (c,d) Spectrum of the shock accelerated protons.
We also note that the proton energy of~0.54 MeV that would result from the density discontinuity motion seen in Fig. 8a is in reasonable agreement with the red spectrum shown in Fig. 4a, which corresponds to a peak density of the gas jet of 2.5n cr , and a 0 ~1. Such reasonable correspondence between the simulated and measured proton energy suggests that reflection of ions on the discontinuity, i.e. the CSA mechanism, observed in the simulations is indeed at play in the experiment.
Moreover, we could analyze in the simulations the velocity of the recessing point at which laser field reflection occurs, i.e. the HB velocity; the results are shown in Table 1.
Hence, the simulations clearly demonstrate that, in conditions of high density (all these simulations are performed with 2.5 n cr as the peak density), the dominant electron populations are characterized by a density spike propagating faster than the hole-boring (and in front of it). This is another indication that indeed CSA is at play here.
Finally, we have compared these velocities with respect to the measured plasma electron temperature in the simulations to verify that it did not affect shock formation, or the shock velocity. The plasma electron temperature (T e ) is here measured in the upstream region at the time when the hole boring starts and the shock is formed. For a 0 = 1, T e ~0.12 MeV (for both the red and blue profiles of Fig. 6), yielding a sound speed around c s = 0.011 c. Stockem-Novo et al.72 state that for near-critical density targets, the shock is launched if v hb > c s , which is the case here, referring to the v hb given in Table 1. Moreover, as v hb ≪ c, we expect that v sh /v hb = 4/3, which is indeed verified in Table 1. For a 0 = 4, T e ~1 MeV (at maximum, i.e. at the peak of the laser irradiation on target), yielding c s = 0.033 c. Again, we verify (see Table 1) v hb > c s , and that as well v sh /v hb ~4/3. This further corroborates that shock acceleration is here at play, with velocities following theoretical scalings.
Conclusions
We have demonstrated the ability to accelerate protons through possibly the CSA process with a 1.054 μm laser and we have observed that there are certainly trends that should be emphasized since they greatly affect the efficiency of CSA. First, we should note that the features in the spectrum are controllable by changing the peak density in the gas jet, and can be optimized (see below) by reducing its thickness. Indeed, we had observed that as the density of the gas jet increased, so did the peak energy of the quasi-monoenergetic bunch. Furthermore, the minimum required density to observe a peaked proton beam was, in our case where we used a laser with wavelength of 1.054 μm, above n cr = 1 × 1021 1/cm 3. Thirdly, the angular distribution is also sensitive to the gas jet density; we observed that the higher the density, the broader the angular distribution.
Interestingly, the PIC simulations point out to, at high densities, a CSA acceleration mechanism since the highest energy protons are accelerated by a density spike that travels through the target at a velocity higher than the HB one. The experimental data at high density are seen also to be close to existing CSA analytical scalings. This last point could be of interest for assessing focal intensity on target at future high-intensity facilities (GIST, APOLLON, ELI, etc.) for which such measurement at the actual target location is still a challenge.
As a perspective, we have explored the effect of further reducing the thickness of the near-critical density profile in the target. For this, we tested (using the hydrodynamic code) what was the effect of having an even longer prepulse interacting with the gas jet. This is shown in Fig. 6a: the red profile shows that when prolonging up to 1.9 ns the prepulse irradiation (i.e. longer than actually used in the experiment), we can indeed shorten even further the gas jet profile. Of course, this would induce the main laser pulse to be even more defocused. This was compensated in the simulations shown in Fig. 9 by keeping the laser intensity on the critical density interface at a 0 = 1 or a 0 = 4. When using this shortened profile and these laser intensities, the resulting proton beam parameters obtained in the PIC simulations are shown in Fig. 9. It can be seen that reducing the thickness of the plasma, i.e. the amount of plasma on the back side, can indeed improve significantly the final proton energy. In the case with a thicker target (as explored in the experiment and shown in Figs 6 and 7), the proton energy is low, but the spectral bandwidth is small. In the case where the target is thinned out, with also a decrease of 2.5 times of the peak target density, we observe that we can obtain much higher final proton energy (see Fig. 9d), but here with some cost on the bandwidth, which is significantly larger. Testing such reduced width critical density gas jet will be explored in further experiments, either by changing the prepulse parameters or by using directly thinner gas jets.
References
Borghesi, M. et al. Fast Ion Generation by High-Intensity Laser Irradiation of Solid Targets and Applications. Fusion Sci. Technol. 49, 412 (2006).
Fuchs, J. et al. Laser acceleration of low emittance, high energy ions and applications. C. R. Physique 10, 176–187 (2009).
Daido, H., Nishiuchi, M. & Pirozhkov, A. S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 75, 056401 (2012).
Macchi, A., Borghesi, M. & Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 85, 751–793 (2013).
Borghesi, M. et al. Electric field detection in laser-plasma interaction experiments via the proton imaging technique. Phys. Plasmas 9, 2214 (2002).
Romagnani, L. et al. Dynamics of Electric Fields Driving the Laser Acceleration of Multi-MeV Protons. Phys. Rev. Lett. 95, 195001 (2005).
Mackinnon, A. J. et al. Proton Radiography of a Laser-Driven Implosion. Phys. Rev. Lett. 97, 045001 (2006).
Chen, S. N. et al. Focusing Dynamics of High-Energy Density, Laser-Driven Ion Beams. Phys. Rev. Lett. 108, 055001 (2012).
Patel, P. K. et al. Isochoric Heating of Solid-Density Matter with an Ultrafast Proton Beam. Phys. Rev. Lett. 91, 125004 (2003).
Antici, P. et al. Isochoric heating of matter by laser-accelerated high-energy protons. Journal de Physique IV 133, 1077 (2006).
Snavely, R. A. et al. Laser generated proton beam focusing and high temperature isochoric heating of solid matter. Physics of Plasmas 14, 092703 (2007).
Roth, M. et al. Fast Ignition by Intense Laser-Accelerated Proton Beams. Phys. Rev. Lett. 86, 436 (2001).
Bulanov, S. V. et al. Oncological hadrontherapy with laser ion accelerators. Phys. Rev. A 299, 240 (2002).
Malka, V. et al. Practicability of protontherapy using compact laser systems. Med. Phys. 31, 1587 (2004).
Linz, U. & Alonso, J. What will it take for laser driven proton accelerators to be applied to tumor therapy? Phys. Rev. Special Topics – Accel. and Beams 10, 094801 (2007).
Leemans, W. P. et al. The Berkeley Lab Laser Accelerator (BELLA): A 10 GeV laser plasma accelerator, in Advanced Accelerator Concepts: 14th Workshop, edited by S. H. Gold and G. S. Nusinovich, American Institute of Physics (2010).
Papadopoulos, D. Z. et al. The Apollon 10 PW laser: experimental and theoretical investigation of the temporal characteristics. High Power Laser Science and Engineering. 4, e34 (2016).
Mourou, G. et al. The future is fibre accelerators. Nat. Phot. 7, 258–261 (2013).
Wilks, S. C. et al. Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 8, 242 (2001).
Hegelich, M. et al. Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 439, 441–444 (2006).
Snavely, R. A. et al. Intense High-Energy Proton Beams from Petawatt-Laser Irradiation of Solids. Phys. Rev. Lett. 85, 2945 (2000).
Bolton, P. R. et al. Instrumentation for diagnostics and control of laser-accelerated proton (ion) beams. Physica Medica 30, 255–270 (2014).
Macchi, A. et al. Laser Acceleration of Ion Bunches at the Front Surface of Overdense Plasmas. Phys. Rev. Lett. 94, 165003 (2005).
Antici, P. et al. Energetic protons generated by ultrahigh contrast laser pulses interacting with ultrathin targets. Physics of Plasmas 14, 030701 (2007).
Kar, S. et al. Ion Acceleration in Multispecies Targets Driven by Intense Laser Radiation Pressure. Phys. Rev. Lett. 109, 185006 (2012).
Henig, A. et al. Radiation-Pressure Acceleration of Ion Beams Driven by Circularly Polarized Laser Pulses. Phys. Rev. Lett. 103, 245003 (2009).
Dollar, F. et al. Finite Spot Effects on Radiation Pressure Acceleration from Intense High-Contrast Laser Interactions with Thin Targets. Phys. Rev. Lett. 108, 175005 (2012).
Palmer, C. et al. Rayleigh-Taylor Instability of an Ultrathin Foil Accelerated by the Radiation Pressure of an Intense Laser. Phys. Rev. Lett. 108, 225002 (2012).
Wilks, S., Kruer, W. L., Tabak, M. & Langdon, A. B. Absorption of Ultra-Intense Laser Pulses. Phys. Rev. Lett. 69, 1383 (1992).
Sentoku, Y. et al. High energy proton acceleration in interaction of short laser pulse with dense plasma target. Phys. Plasmas 10, 2009 (2003).
Matsukado, K. et al. Energetic Protons from a Few-Micron Metallic Foil Evaporated by an Intense Laser Pulse. Phys. Rev. Lett. 91, 215001 (2003).
Yogo, A. et al. Laser ion acceleration via control of the near-critical density target. Phys. Rev. E 77, 016401 (2008).
Bulanov, S. V. & Esirkepov, T. Z. Comment on “Collimated Multi-MeV Ion Beams from High-Intensity Laser Interactions with Underdense Plasma”. Phys. Rev. Lett. 98, 049503 (2007); Willingale, L., et al., Reply. Phys. Rev. Lett. 98, 049504 (2007).
Bulanov, S. S. et al. Generation of GeV protons from 1 PW laser interaction with near critical density targets. Phys. Plasmas 17, 043105 (2010).
Nakamura, T. et al. High-Energy Ions from Near-Critical Density Plasmas via Magnetic Vortex Acceleration. Phys. Rev. Lett. 105, 135002 (2010).
Denavit, J. Absorption of high-intensity subpicosecond lasers on solid density targets. Phys. Rev. Lett. 69, 3052 (1992).
Silva, L. et al. Proton Shock Acceleration in Laser-Plasma Interactions. Phys. Rev. Lett. 92, 015002 (2004).
Atzeni, S. & Meyer-ter-Vehn, J. The Physics of Inertial Fusion, Clarendon Press.
Moiseev, S. S. & Sagdeev, R. Z. Collisionless shock waves in a plasma in a weak magnetic field. J. Nucl. Energy, Part C Plasma Phys. 5, 43 (1963).
Moreau, J. G., d’Humières, E., Nuter, R. & Tikhonchuk, V. T. Stimulated Raman scattering in the relativistic regime in near-critical plasmas. Phys. Rev. E 95, 013208 (2017).
d’Humières, E. et al. Investigation of high intensity laser proton acceleration with underdense targets. J. Phys.: Conf. Ser. 244, 042023 (2010).
Gauthier, M. et al. Investigation of longitudinal proton acceleration in exploded targets irradiated by intense short-pulse laser. Phys. Plasmas 21, 013102 (2014).
Antici, P. et al. Acceleration of collimated 45 MeV protons by strong collisionless shocks driven in large-scale gradient low-density plasmas irradiated by a 1020 W/cm2, 1 µm wavelength laser, submitted; arxiv: 1708.02539.
Fiuza, F. et al. Laser-Driven Shock Acceleration of Monoenergetic Ion Beams. Phys. Rev. Lett. 109, 215001 (2012).
Fuchs, J. et al. Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2, 48–54 (2006).
Prencipe, I. et al. Targets for high repetition rate advanced laser facilities: needs, challenges and perspectives. High Power Laser Science and Engineering 5, e17 (2017).
Campargue, R. Progress in Overexpanded Supersonic Jets and Skimmed Molecular Beams in Free-Jet Zones of Silence. J. Phys. Chem. 88, 4466 (1984).
Palmer, C. et al. Monoenergetic Proton Beams Accelerated by a Radiation Pressure Driven Shock. Phys. Rev. Lett. 106, 014801 (2011); Haberberger, D. et al. Collisionless shocks in laser-produced plasma generate monoenergetic high-energy proton beams. Nature Physics 8, 95 (2012); Tresca, O. et al. Spectral Modification of Shock Accelerated Ions Using a Hydrodynamically Shaped Gas Target. Phys. Rev. Lett. 115, 094802 (2015).
Akhiezer, A. I. & Polovin, R. V. Theory of Wave Motion of an Electron Plasma. Sov. Phys. JETP 3, 696 (1956).
Malka, V. et al. Characterization of neutral density profile in a wide range of pressure of cylindrical pulsed gas jets. Review of Scientific Instruments 71, 2329 (2000).
Danson, C., Hillier, D., Hopps, N. & Neely, D. Petawatt class lasers worldwide. High Power Laser Science and Engineering 3, e3 (2015).
Chen, S. N. et al. Density and temperature characterization of long-scale length, near-critical density controlled plasma produced from ultra-low density plastic foam. Sci. Rep. 6, 21495 (2016).
Chen, S. N. et al. Proton stopping power measurements using high intensity short pulse lasers produced proton beams. Nuclear Instrum. and Methods A 740, 105 (2014).
Sylla, F. et al. Development and characterization of very dense submillimetric gas jets for laser-plasma interaction. Rev. of Sci. Instrum. 83, 033507 (2012).
Helle, M. H. et al. Laser-Accelerated Ions from a Shock-Compressed Gas Foil. Phys Rev Lett 117, 165001 (2016).
Mancic, A., Fuchs, J., Antici, P., Audebert, P. & Gaillard, S. A. Absolute calibration of photostimulable image plate detectors used as (0.5–20 MeV) high-energy proton detectors. Rev Sci Instrum. 79, 073301 (2008).
Svensson, K. et al. Supersonic jets of hydrogen and helium for laser wakefield acceleration. Physical Review Accelerators and Beams 19, 051301 (2016).
Schmid, K. & Veisz, L. Supersonic gas jets for laser-plasma experiments. Review of Scientific Instruments 83, 053304 (2012).
Semushin, S. & Malka, V. High density gas jet nozzle design for laser target production. Review of Scientific Instruments 72, 2961 (2001).
Lemos, N., Lopes, N., Dias, J. M. & Viola, F. Design and characterization of supersonic nozzles for wide focus laser-plasma interactions. Review of Scientific Instruments 80, 103301 (2009).
Park, J., Baldis, H. A. & Chen, H. The implementation and data analysis of an interferometer for intense short pulse laser experiments. High Power Laser Science and Engineering 4, e26 (2016).
Hey, D. S. et al. Laser-accelerated proton conversion efficiency thickness scaling. Phys. of Plasmas 16, 123108 (2009).
Aliverdiev, A. et al. Hydrodynamics of laser-produced plasma corona measured by optical interferometry. Plasma Phys. Control. Fusion 50, 105013 (2008).
Borghesi, M. et al. Characterization of laser plasmas for interaction studies: Progress in time-resolved density mapping. Phys. Rev. E 54, 6769 (1996).
Willi, O., Evans, R. G. & Raven, A. Time resolved density profiles of laserheated plasmas. Physics of Fluids 23, 2061 (1980).
Börner, M. et al. Development of a Nomarski-type multi-frame interferometer as a time and space resolving diagnostics for the free electron density of laser-generated plasma. Review of Scientific Instruments 83, 043501 (2012).
La fusion thermonucléaire par laser, vol. 2, R. Dautray et al. (Editors), Eyrolles, Paris (1994); Dattolo, E. et al. Status of our understanding and modeling of x-ray coupling efficiency in laser heated hohlraums. Physics of Plasmas 8, 260 (2001).
Kaiser, T. B. Laser ray tracing and power deposition on an unstructured three-dimensional grid. Phys. Rev. E 61, 892 (2000).
Marion, D., Debayle, A., Masson-Laborde, P.-E., Loiseau, P. & Casanova, M. Modeling crossed-beam energy transfer for inertial confinement fusion. Phys. Plasmas 23, 052705 (2016).
Masson-Laborde, P.-E. et al. Laser plasma interaction on rugby hohlraum on the Omega Laser Facility: Comparisons between cylinder, rugby, and elliptical hohlraums. Phys. Plasmas 23, 022703 (2016).
Willingale, L. et al. Collimated Multi-MeV Ion Beams from High-Intensity Laser Interactions with Underdense Plasma. Phys. Rev. Lett. 96, 245002 (2006).
Stockem Novo, A., Kaluza, M. C., Fonseca, R. A. & Silva, L. O. Optimizing laser-driven proton acceleration from overdense targets. Sci. Rep. 6, 29402 (2016).
Ping, Y. et al. Absorption of Short Laser Pulses on Solid Targets in the Ultrarelativistic Regime. Phys. Rev. Lett. 100, 085004 (2008).
Fonseca, R. A. et al. OSIRIS: A Three-Dimensional, Fully Relativistic Particle in Cell Code for Modeling Plasma Based Accelerators. Lecture Notes in Computer Science 2331, 342 (2002).
Brady, C. S. & Arber, T. D. An ion acceleration mechanism in laser illuminated targets with internal electron density structure. Plasma Phys. Contr. Fusion 53, 015001 (2011).
Acknowledgements
The authors thank the staff of the Titan Laser and the Jupiter Laser facility for their support during the experimental preparation and execution. We thank R. C. Cauble and J.R. Marquès for fruitful discussions, and R. Riquier for the gas jet characterization. This work was partly done within the LABEX Plas@Par project and supported by Grant No. 11‐IDEX‐0004‐02 and ANR-17-CE30-0026-Pinnacle from Agence Nationale de la Recherche. It has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no 654148 Laserlab-Europe, and was supported in part by the Ministry of Education and Science of the Russian Federation under Contract No. 14.Z50.31.0007. The use of the Jupiter Laser Facility was supported by the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. This work is supported by FRQNT (nouveaux chercheurs, Grant No. 174726, Team Grant 2016-PR-189974), NSERC Discovery Grant (Grant No. 435416), ComputeCanada (Job: pve-323-ac, P. Antici). M.V. and L.O.S. were supported by the European Research Council (ERC-2010-AdG grant no. 267841). O.Willi acknowledges the DFG Programmes GRK 1203 and SFB/TR18. M. B.-G., J. J. S., and E. d.’H. acknowledge the funding from the project ARIEL (Conseil Regional d’Aquitane); their work was carried out in the framework of the Investments for the Future Programme IdEn Bordeaux LAPHIA (ANR-10-iDEX-03-02). The PIC simulations were performed at Fermi/Marconi (Italy) through PRACE allocation and at the Accelerates cluster (Lisbon, Portugal).
Author information
Authors and Affiliations
Contributions
J.F., S.N.C. and E.d.H. conceived the projet. S.N.C. wrote the manuscript, made Figures 1, 2, 4, and 5 organized and lead the experiment, and analysed the data from the proton spectrometers; M.V. performed the PIC simulations, as well as their analysis, and made Figures 6, 7, 8 and 9; T.G. prepared the experiment, laser and diagnostic alignment and characterized the gas nozzles; E.B. gave valuable insight in the interpretation of the P. I. C. simulation results and performed post-processing of the results; P.A. participated in the experiment; MBG fielded diagnostics during the experiment; P.L. performed the hydrodynamic simulations using FCI2 and made Figure 3; H.P. supervised students and participated in the experiment; G.R. prepared the experiment, laser and diagnostic alignment; J.J.S. supported the experiment and students financially; A.M.S. participated in the experiment and fielded diagnostics; M.S. supervised the data analysis and revised the manuscript; O.W. supervised students and provided financial support, J.F. supervised fielding the experiment, the data analysis and helped write the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, S.N., Vranic, M., Gangolf, T. et al. Collimated protons accelerated from an overdense gas jet irradiated by a 1 µm wavelength high-intensity short-pulse laser. Sci Rep 7, 13505 (2017). https://doi.org/10.1038/s41598-017-12910-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-12910-6
- Springer Nature Limited
This article is cited by
-
Laser-driven multi-MeV high-purity proton acceleration via anisotropic ambipolar expansion of micron-scale hydrogen clusters
Scientific Reports (2022)
-
Electrostatic shock acceleration of ions in near-critical-density plasma driven by a femtosecond petawatt laser
Scientific Reports (2020)
-
Efficient Laser-Driven Proton Acceleration from a Cryogenic Solid Hydrogen Target
Scientific Reports (2019)
-
Experimental evidence for the enhanced and reduced stopping regimes for protons propagating through hot plasmas
Scientific Reports (2018)
-
Ultra-intense laser interaction with nanostructured near-critical plasmas
Scientific Reports (2018)