Abstract
Artificial atom qubits in diamond have emerged as leading candidates for a range of solid-state quantum systems, from quantum sensors to repeater nodes in memory-enhanced quantum communication. Inversion-symmetric group IV vacancy centers, comprised of Si, Ge, Sn, and Pb dopants, hold particular promise as their neutrally charged electronic configuration results in a ground-state spin triplet, enabling long spin coherence above cryogenic temperatures. However, despite the tremendous interest in these defects, a theoretical understanding of the electronic and spin structure of these centers remains elusive. In this context, we predict the ground-state and excited-state properties of the neutral group IV color centers from first principles. We capture the product Jahn–Teller effect found in the excited state manifold to second order in electron–phonon coupling, and present a nonperturbative treatment of the effect of spin–orbit coupling. Importantly, we find that spin–orbit splitting is strongly quenched due to the dominant Jahn–Teller effect, with the lowest optically-active 3Eu state weakly split into ms-resolved states. The predicted complex vibronic spectra of the neutral group IV color centers are essential for their experimental identification and have key implications for use of these systems in quantum information science.
Similar content being viewed by others
Introduction
Artificial atoms in diamond are promising candidates for a wide variety of quantum technologies1,2,3,4,5, including as quantum repeaters for long-range quantum networks6,7. Many milestones have been reached using the nitrogen-vacancy (NV−) center8,9 and more recently the SiV−10,11,12,13,14. Further exploration of novel defect candidates has included the GeV−15,16,17,18, SnV−19,20,21,22, PbV−23,24, and SiV025,26,27, all of which have been observed experimentally and described theoretically28,29. The neutrally-charged SiV0 has symmetry analogous to the SiV−, but its missing electron gives rise to a triplet ground state as found in the NV−, with the corresponding potential for both long spin coherence times and symmetry-protected optical transitions. Theoretical work has postulated the remaining group IV neutral (IV0) centers29 (GeV0, SnV0, and PbV0) and described the negatively-charged group III defect centers30 as isoelectronic to the SiV0. Calculations suggest that all of these defect candidates are thermodynamically more likely to exist in intrinsic diamond than the SiV0, which requires p-type doping27. Within this growing space of candidate artificial atom qubits, an ab initio understanding of the level structure is required to harness the advantages of each emitter in quantum science31.
Accurate descriptions of artificial atoms in diamond can be particularly challenging because of the dominant Jahn–Teller (JT) distortions32 present. In such systems, the total energy of a JT-unstable electronic configuration is lowered as a result of the coupling of the electronic structure to nuclear motion, introducing electron–phonon interactions. In the case of group IV0 defects, the excited state exhibits a product Jahn–Teller (pJT) effect which results from simultaneous Jahn–Teller instabilities in two orbitals29,33,34,35. The pJT interaction leads to either a dynamical or static JT effect, or a mixture of both. In the case of a dynamical JT distortion, the system is best described as a collective electron–vibration (vibronic) system. This strong coupling of electronic and vibrational states may modify electronic observables, for example a quenching of spin–orbit (SO) coupling (SOC).
Including the pJT effect is therefore critical for predictions of the zero-phonon line (ZPL) transition energies and the excited-state level structure. Previous work has found that describing pJT interactions to first order in coupling explains the observed energy splitting25 between the optically-bright Eu and dark A2u states for SiV029. An important effect to consider, particularly for the heavier group IV0 defects, is the role of spin–orbit interactions, as these defects can have coupling constants on the order of 100s of meV28. The interplay of SOC interactions and JT physics in the excited-state of group IV0 centers has significant impact on the expected SO behavior if the JT effect couples the electrons and phonons strongly, as we find.
In this article, we describe the combined impact of spin–orbit and Jahn–Teller interactions in the neutral group IV centers in diamond from first principles. We describe the product Jahn–Teller effect to second order in electron–phonon coupling and find a large second order energy shift. Importantly, the effects of spin–orbit coupling are included nonperturbatively and splittings are found to be an order of magnitude smaller than expected for a purely electronic system as a result of the JT interaction. These fine structure details reveal additional physics of color center qubits in diamond and present a pathway to identify GeV0, SnV0, and PbV0 experimentally.
Results
Electronic structure
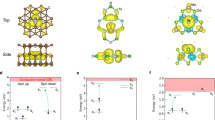
The group IV centers in diamond adopt a split-vacancy configuration within the diamond lattice, where the dopant group IV atom sits between two vacant carbon sites, as shown in Fig. 1a and denoted by the point group D3d. The defect introduces localized electronic orbitals comprised of the dangling bonds of the nearby carbon atoms and the dopant atom, which can be captured using density functional theory (DFT)36 (see “Methods” section for computational details) and are labeled by their symmetry. The energetically-relevant orbitals are of eu and eg character and exist near and above the valence band of intrinsic diamond, respectively, shown schematically in Fig. 1b. Both the eu and eg orbitals are doubly-degenerate and can be further labeled by their spatial orientation, i.e., {eu} = {eux, euy} and similarly {eg} = {egx, egy}. Including spin, these levels combined can host up to eight electrons. For group IV0 centers, six electrons are present in the (eueg) manifold. Equivalently, we can describe these electronic states in the basis of two defect-bound holes. We choose to adopt this convention for the remainder of this article.
a Lattice configuration of the group IV0 defects, in which the impurity atom (blue) sits between two vacant carbon sites (gray). b Simplified energy level diagram showing the energy location of the doubly-degenerate eu and eg orbitals relative to the band gap of bulk diamond. The ground state is a spin triplet and the corresponding excited state undergoes a symmetry-breaking pJT distortion (right) as a result of orbital instabilities in both the eu and eg orbitals. c Potential energy surfaces computed for the pJT system including effects up to 2nd order in coupling. Here we label the energy instability by \({E}_{{\rm{JT}}}^{{\mathrm{(i)}}}\) for the result of constructive (i = 1) and destructive (i = 2) interference of the two orbital branches. The axial asymmetry arises from a second order effect denoted similarly by the parameter \({\delta }_{{\rm{JT}}}^{{\mathrm{(i)}}}\). The black curves indicate 1D cuts through the 2D (Qx, Qy) distortion space, which allows us to fully parameterize the system. d DFT-obtained potential energy surfaces along these 1D cuts for the SnV0 defect. The D3d high-symmetry point (Qx = 0 Å) is found to be unstable in two surfaces, consistent with the pJT picture. We also label the displacement amplitudes \({\rho }_{0}^{{\mathrm{(i)}}}\) from the D3d to the C2h minima. The splitting Λ is a result of static electronic correlation. All values are tabulated in Table 1.
The ground state has the hole configuration \({e}_{{\mathrm{g}}}^{2}\) (\({e}_{{\mathrm{gx}}}^{1}{e}_{{\mathrm{gy}}}^{1}\)), and prefers the triplet S = 1 spin configuration. The total defect wavefunction is of 3A2g symmetry, and is directly obtained from electronic structure calculations. In constructing the total wavefunction, given the symmetric triplet spin component, we ensure that the orbital wavefunction is antisymmetrized; this is given by the \({\mathcal{A}}\) symbol. The ground state orbital wavefunction can be written as \({\mathcal{A}}\left|{e}_{{\mathrm{gx}}}{e}_{{\mathrm{gy}}}\right\rangle\,=\,1/\sqrt{2}\left({e}_{{\mathrm{gx}}}({{\bf{r}}}_{1}){e}_{{\mathrm{gy}}}({{\bf{r}}}_{2})-{e}_{{\mathrm{gx}}}({{\bf{r}}}_{2}){e}_{{\mathrm{gy}}}({{\bf{r}}}_{1})\right)\). In the excited electronic configuration, one hole moves from an eg to an eu orbital. Unlike in the ground state, there exist four distinct hole occupations with this \({e}_{{\mathrm{g}}}^{1}{e}_{{\mathrm{u}}}^{1}\) configuration. The antisymmetrized orbital wavefunctions are given by \({\mathcal{A}}\left|{e}_{{\mathrm{ux}}}{e}_{{\mathrm{gx}}}\right\rangle\), \({\mathcal{A}}\left|{e}_{{\mathrm{uy}}}{e}_{{\mathrm{gx}}}\right\rangle\), \({\mathcal{A}}\left|{e}_{{\mathrm{ux}}}{e}_{{\mathrm{gy}}}\right\rangle\), and \({\mathcal{A}}\left|{e}_{{\mathrm{uy}}}{e}_{{\mathrm{gy}}}\right\rangle\). We can construct the irreducible representations of the triplet subspace as linear combinations of these orbital states, as has been done previously29.
Jahn–Teller interaction
Each of these antisymmetrized states obtained from our ab initio calculations are Jahn–Teller unstable, in that they energetically prefer a configuration with the lower symmetry C2h point group to that with the higher symmetry D3d point group. We note that despite the lower symmetry, the C2h point group is still inversion-symmetric. The nuclear motion associated with these distortions is a result of interactions with phonon modes of symmetry Eg. In contrast with the single JT system (Eg ⊗ e), the JT distortion found in the excited state of group IV0 systems is due to simultaneous JT interactions in both the eu and eg orbitals. This collective product Jahn–Teller behavior is denoted by Eg ⊗ eu ⊗ eg and shown schematically in the right panel of Fig. 1b. Previous work has covered the single JT to second order as well as the pJT32,33,35 to first order in electron–phonon coupling. Here, we describe the coupling of the two electronic states with the Eg-type vibrational mode to second order in vibrational coupling. The Hamiltonian for this interaction can be written as:
The first two lines represent linear coupling with coupling constants Fu/g while the latter two represent quadratic coupling terms with coupling constants Gu/g for both the eg and eu orbital branches. The nuclear component of the Hamiltonian is written with \(\hat{X}\) and \(\hat{Y}\) representing bosonic operators for the phonons given by \(\{\hat{X},\hat{Y}\}\,=\,({\hat{a}}_{\{{\mathrm{x,y}}\}}^{\dagger }+{\hat{a}}_{\{{\mathrm{x,y}}\}})/\sqrt{2}\) and the electronic component in terms of \({\hat{\sigma }}_{i}\) which are the standard Pauli and unit matrices acting on the eu ⊗ eg subspace. The Hamiltonian in Eq. (1) is defined within the single-excitation two-particle hole manifold, therefore the basis states are \({\mathcal{A}}\left|{e}_{{\mathrm{ux}}}{e}_{{\mathrm{gx}}}\right\rangle\), \({\mathcal{A}}\left|{e}_{{\mathrm{uy}}}{e}_{{\mathrm{gx}}}\right\rangle\), \({\mathcal{A}}\left|{e}_{{\mathrm{ux}}}{e}_{{\mathrm{gy}}}\right\rangle\), and \({\mathcal{A}}\left|{e}_{{\mathrm{uy}}}{e}_{{\mathrm{gy}}}\right\rangle\), which are captured from electronic structure calculations. For Eq. (1), we note that there can exist different sign conventions; in this work we adopt the sign convention commonly applied to Jahn–Teller Hamiltonians28,32,37,38.
In the pJT case, two independent solutions which are unstable at the high-symmetry point can exist. One corresponds to the constructive interference of the two JT distortions \(( \sim \!\!{({F}_{{\mathrm{g}}}+{F}_{{\mathrm{u}}})}^{2})\) and the other to the destructive interference \(( \sim \!\!{({F}_{{\mathrm{g}}}-{F}_{{\mathrm{u}}})}^{2})\), as shown in Fig. 1c. To find the coupling constants and solve for the coupled vibronic states, we obtain displacement \({\rho }_{0}^{{\mathrm{(i)}}}\) and energy \({E}_{{\rm{JT}}}^{{\mathrm{(i)}}}\), \({\delta }_{{\rm{JT}}}^{{\mathrm{(i)}}}\) parameters from the defect potential energy surfaces (PES) computed from first principles electronic structure, where i = 1, 2 for the constructive and destructive pJT, respectively. For the SnV0 color center we show the resulting adiabatic PES as a one-dimensional cut along Qy = 0 in Fig. 1d (see Supplementary Fig. 1 for similar plot including all group IV0 defects). In principle the PES are two-dimensional, with the minima being threefold degenerate (see Fig. 1c). However, due to the symmetry of the PES, this 1D cut completely parameterizes the pJT Hamiltonian. For additional details on connecting the coupling constants in Eq. (1) to our calculations, refer to Supplementary Note 2 and Supplementary Table 1.
In these defect systems electronic correlation \(\hat{{\rm{W}}}\) plays a role in splitting the electronic states for reasons distinct from the Jahn–Teller physics. This correlation can be incorporated along the lines of previous work29, leading to the following total Hamiltonian for the system:
Here, \({\hat{{\rm{H}}}}_{{\rm{osc}}}\,=\,\hslash {\omega }_{{\mathrm{E}}}{\sum }_{{\mathrm{i}} = {\mathrm{x,y}}}\left({{\hat{a}}_{{\mathrm{i}}}^{\dagger }{\hat{a}}_{{\mathrm{i}}}+1/2}\right)\) is the two-dimensional harmonic oscillator Hamiltonian for the Eg phonon modes of energy \(\hbar\)ωE which couple with the electronic states via the term \({\hat{{\rm{H}}}}_{{\rm{pJT}}}^{(2)}\). The term \(\hat{{\rm{W}}}\) represents the effects of static electronic correlation, which causes the energy splitting Λ between the two branches of the potential energy surface shown in Fig. 1d.
Spin–orbit interaction
Next we describe spin–orbit interactions in the pJT system. In the presence of a dynamical JT effect, expectation values of purely electronic operators can be quenched because of the coupled vibronic nature of the system, as first shown by Ham39. Thus it is important to analyze the effects of SO interactions with caution, as has already been demonstrated for the group IV− defects28. In these group IV0 centers, the SOC Hamiltonian can be written as a product of the single-hole interactions37, since the spin–orbit coupling does not mix the eu and eg orbitals40. The SOC Hamiltonian is written as
Here, we introduce SO splittings \({\lambda }_{{\mathrm{u/g}}}^{0}\) for both the eu and eg orbitals, which can be obtained from ab initio calculations. The variable ms corresponds to eigenvalues of \({\hat{S}}_{{\mathrm{z}}}\) and for the S = 1 triplet system can take on values of ms ∈ [1, 0, −1]. While SOC in its general \(\hat{{\bf{L}}}\cdot \hat{{\bf{S}}}\) form (with angular momentum operator \(\hat{{\bf{L}}}\) and spin operator \(\hat{{\bf{S}}}\)) also contains transverse terms, these transverse terms only couple eg/eu orbitals to a2u orbitals which are outside the (eg, eu) manifold of interest40. This consideration allows us to effectively write \({\hat{{\rm{H}}}}_{{\rm{SOC}}}\) solely in terms proportional to \({\hat{L}}_{{\mathrm{z}}}{\hat{S}}_{{\mathrm{z}}}\), yielding Eq. (3). The \({\hat{L}}_{{\mathrm{z}}}{\hat{S}}_{{\mathrm{z}}}\) interactions can couple the excited-state singlet manifold with the ms = 0 excited-state triplets, however we choose to consider only the triplet subspace as the \(({e}_{{\mathrm{u}}}^{1}{e}_{{\mathrm{g}}}^{1})\) singlet excited states are expected to be higher in energy due to Coulomb repulsion26. Ultimately intersystem crossing (ISC) rates between these triplet and singlet levels will likely depend on phonon overlaps of the full diamond + defect system, however they require nonzero spin–orbit coupling and thus our analysis is important for further understanding ISC.
To capture the spin–orbit interaction in addition to the pJT physics, we find that including SOC perturbatively is insufficient, even for the SiV0 system. Thus, we invoke a complete spin-resolved orbital basis including all spin sublevels of Eq. (3). From this we perform direct diagonalization of the combined spin–orbit and Jahn–Teller system (see Supplementary Note 5), where we take all terms in Eq. (2) to be spin-independent. The solutions of this coupled Hamiltonian allows us to extract both the absolute energy shifts of our vibronic eigenstates with SO effects and the effective SO splittings between spin sublevels nonperturbatively.
Discussion
Table 1 summarizes the results of our work. In each of the defect centers studied, we find a significant pJT effect, with the constructive interference yielding instabilities of over 200 meV. We find the second order effects are also relatively large, with \({\delta }_{{\rm{JT}}}^{(1)} \sim 0.3{E}_{{\rm{JT}}}^{(1)}\) for each of the defects studied. These second order shifts are important, as they represent the energy barrier between the three energy minima present in the 2D vibrational (Qx, Qy) space. This energy barrier helps to determine if the system will prefer a static or dynamic JT distortion, the latter of which means the electron and phonon degrees of freedom cannot be decoupled and instead a coupled vibronic solution is required. Indeed, the system can be parameterized as strongly-coupled as given by the parameter λ = EJT/\(\hbar\)ωE, which is >2 for all cases studied here. After calculation of the parameters in Table 1, we can solve for the coupled electron-vibrational system as defined in Eqs. (1, 2).
Figure 2 visualizes our results for SnV0 (See Supplementary Figs. 2–5 for similar plots of all group IV0 defects). Panel a represents the adiabatic states along a 1D cut of the vibrational space with Qy = 0. The full vibronic solutions to Eq. (2) are shown in panel b, plotted as a function of the expectation value of displacement from the high-symmetry D3d minima. In both cases, we can project the solutions onto the irreducible states of the D3d excited-state manifold, with the color legend given in panel c. We find that the lowest energy states are comprised of roughly equal contributions from the undistorted \({\left.\right|}^{3}{E}_{{\mathrm{ u}}}\left.\right\rangle\) and \({\left.\right|}^{3}{A}_{2{\mathrm{u}}}\left.\right\rangle\) electronic states. This is true for the quadratic coupling as well. In Fig. 2d we specifically focus on the lowest-energy vibronic solutions. The lowest vibronic state has total symmetry A2u which is optically dark, whereas the next eigenstate is an optically-active, doubly-degenerate Eu level. In first order pJT, the splitting γ(1) between these two states for SnV0 is 8.96 meV, while including second-order coupling decreases splitting γ(2) to just 6.22 meV. Even at second order, the 3Eu state remains degenerate, however overall the eigenstates of the system shift upwards in energy by roughly 20 meV.
a 1D cut (Qy = 0) of the full electron-vibration coupled PES within the adiabatic approximation for SnV0. b The vibronic eigenstates found after solving the pJT and electronic correlation Hamiltonian (Eq. (2)), where the x-axis corresponds to the expectation value of the nuclear position coordinate \(R=\sqrt{{Q}_{{\mathrm{ x}}}^{2}+{Q}_{{\mathrm{y}}}^{2}}\) relative to the D3d minima. The solutions for both a and b are projected onto the D3d symmetry-adapted electronic states and the resulting composition is represented by the color shown in c. d The effects of 2nd order JT and explicit inclusion of SOC are detailed for the lowest-energy eigenstates of the system. In 1st and 2nd order JT, the A2u state is nondegenerate and the Eu state is twice degenerate. The inclusion of second order decreases the splitting γ between these levels, while also introducing an absolute energy shift of around 20 meV. The inclusion of SOC splits the Eu levels into \({E}_{{\mathrm{u}}}^{+}\) and \({E}_{{\mathrm{u}}}^{-}\), each with corresponding ms sublevels. The splitting between the ms = ±1 levels is given by λg + λu, which is strongly attenuated. The ms = 0 (labeled by \(\left.| {\mathcal{S}}| \uparrow \downarrow \right\rangle\)) levels are unaffected by SOC.
It is interesting to note that in general including second-order terms in the pJT Hamiltonian decreases the splitting γ between the lowest vibronic states (see Table 1). This splitting was measured experimentally for SiV025 to be 6.8 meV; here we find a larger discrepancy to experiment in the case of quadratic coupling (γ(2) = 3.2 meV) than we do for linear coupling (γ(1) = 7.2 meV). We emphasize, however, that an inclusion of second order electron–phonon coupling more closely resembles the ab initio data, as can be seen in Fig. 1d due to the nonvanishing \({\delta }_{{\rm{JT}}}^{{\mathrm{(i)}}}\). The origin of this disagreement is unknown and beyond the scope of this work. We suggest that it may represent an energy-resolution limitation in the approach employed. Possible routes to improve the agreement with experiment, which will be analyzed in future work could be an improved model of the static correlation or the use of a different hybrid functional than HSE06. We note that inclusion of higher-order terms41 up to fourth order in electron–phonon interactions is found to negligibly change our results, as the corresponding coupling coefficients for these terms are found to be orders of magnitude smaller than the first and second order terms.
The coupled spin-vibronic results are shown in the final panel of Fig. 2d and are found after including the SOC Hamiltonian directly. We find that the ms = 0 and ms = ±1 sublevels of the A2u vibronic states are split, in the case of SnV0 by 5.9 meV. The ms = ±1 sublevels of the Eu states also split (here we distinguish the Eu states by labels + and −). These \({E}_{{\mathrm{u}}}^{\pm }\) states have a Kramers degeneracy, very much analogous to the lowest Eg vibronic states of the group IV−, where \({\left.\right|}^{3}{E}_{{\mathrm{u}}}^{+}\left.\right\rangle \otimes \left|\uparrow \uparrow \right\rangle\) and \({\left.\right|}^{3}{E}_{{\mathrm{u}}}^{-}\left.\right\rangle \otimes \left|\downarrow \downarrow \right\rangle\) are the degenerate, lowest energy Eu states. These are split by an energy of λu + λg from the degenerate \({\left.\right|}^{3}{E}_{{\mathrm{u}}}^{-}\left.\right\rangle \otimes \left|\uparrow \uparrow \right\rangle\) and \({\left.\right|}^{3}{E}_{{\mathrm{u}}}^{+}\left.\right\rangle \otimes \left|\downarrow \downarrow \right\rangle\) states, as shown in Fig. 2d for SnV0. In the absence of JT interactions this splitting λg + λu would be over 100 meV, however here it is only ~3 meV, a direct consequence of the strong electron–phonon coupling present in the pJT system. Additional interactions such as effects of strain and spin–spin coupling could split and shift these levels further.
For all cases, the reduction factors denoted by pu/g are smaller than 0.05, indicative of a very strong quenching of the SO interaction, even more so than the group IV− color centers. This can be attributed in part to the scaling of the Jahn–Teller instability vs. the spin–orbit splitting in the two-hole case. While to first order the JT energy scales as the square of the coupling (i.e., \(\sim {({F}_{{\mathrm{u}}}+{F}_{{\mathrm{g}}})}^{2}\)), the SO splitting scales linearly (i.e., λg + λu). Such a scaling and the resulting JT energies intuitively explains the significant SO quenching we find in this work. We note that shifts in the absolute energies of the Eu states are found to be most significant in the case of PbV0, where we find a redshift in the predicted ZPL of roughly 0.05 eV. All lighter defects have much weaker absolute energy shifts due to their reduced SO coupling constants. More details and discussion of the SOC approach used here can be found in Supplementary Note 5, including Supplementary Fig. 6 and Supplementary Table 2.
We note that additional theoretical work remains to be done towards understanding these emitters, including the nature of the photoluminescence spectra42, intersystem crossings, and the effects of nonradiative decay channels.
In conclusion, we present first principles calculations of group IV neutral artificial atoms in diamond, where we capture the product Jahn–Teller effect to second order in electron–phonon coupling and nonperturbatively describe the effects of spin–orbit interactions. Our results find significant reduction in the spin–orbit splitting due to the strong pJT. However, we also find that the spin–orbit interactions would split the lowest optically-active states into ms-resolved levels split by up to a few meV in the heavier candidates. These results provide qualitative insight into the physics of artificial atom qubits in diamond, and are of quantitative importance in experimental identification and manipulation of these centers in quantum information science.
Methods
First principles calculations
We employ constrained Kohn–Sham density functional theory calculations performed within the VASP code36 (version 5.4.4). The Kohn–Sham wavefunctions are described using a plane wave basis set with projector-augmented wave (PAW) pseudopotentials. The basis set used corresponds to an energy cutoff of 400 eV. We also performed calculations at stringent 800 eV energy cutoffs and found no appreciable changes in the results. We employ the hybrid HSE06 exchange-correlation functional43,44 to accurately describe the energetics of these defect systems. All calculations were performed with spin polarization. The defects are modeled in a cubic supercell equivalent to 512 carbon atoms of the diamond lattice, with a lattice constant of 6.70 Bohrs (3.545 Å). For such a supercell we sample only the Γ point of the corresponding Brillouin zone.
Ionic relaxation was performed until forces on all atoms fell below 10−2 eV/Å. The excited-state geometries were obtained for the high-symmetry D3d geometry by enforcing symmetry during relaxation. We also relaxed with a C2h symmetry constraint to capture the low-symmetry structures and energy. We also verified these were indeed the lowest-energy structures by removing symmetry constraints and finding no change in ionic positions or total energy.
Solving of Hamiltonians
All subsequent calculations and solving of Hamiltonians are done numerically. We include up to 40 phonons in the expansion of the product Jahn–Teller Hamiltonian (Eq. (1) of the main text). Eigenvalues and eigenvectors are found by diagonalizing the corresponding Hamiltonian.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The developed Python codes used to support the findings of this study are available from the corresponding author upon reasonable request.
References
Atatüre, M., Englund, D., Vamivakas, N., Lee, S.-Y. & Wrachtrup, J. Material platforms for spin-based photonic quantum technologies. Nat. Rev. Mater. 3, 38–51 (2018).
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photon. 12, 516–527 (2018).
Aharonovich, I., Englund, D. & Toth, M. Solid-state single-photon emitters. Nat. Photon. 10, 631–641 (2016).
Rogers, L. J. et al. Multiple intrinsically identical single-photon emitters in the solid state. Nat. Commun. 5, 4739 (2014).
Weber, J. R. et al. Quantum computing with defects. Proc. Natl Acad. Sci. USA 107, 8513–8518 (2010).
Kalb, N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).
Humphreys, P. C. et al. Deterministic delivery of remote entanglement on a quantum network. Nature 558, 268–273 (2018).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Rozpedek, F. et al. Near-term quantum-repeater experiments with nitrogen-vacancy centers: Overcoming the limitations of direct transmission. Phys. Rev. A 99, 052330 (2019).
Rogers, L. J. et al. Electronic structure of the negatively charged silicon-vacancy center in diamond. Phys. Rev. B 89, 235101 (2014).
Hepp, C. et al. Electronic structure of the silicon vacancy color center in diamond. Phys. Rev. Lett. 112, 036405 (2014).
Lemonde, M.-A. et al. Phonon networks with silicon-vacancy centers in diamond waveguides. Phys. Rev. Lett. 120, 213603 (2018).
Evans, R. E. et al. Photon-mediated interactions between quantum emitters in a diamond nanocavity. Science 362, 662–665 (2018).
Sukachev, D. D. et al. Silicon-vacancy spin qubit in diamond: a quantum memory exceeding 10 ms with single-shot state readout. Phys. Rev. Lett. 119, 223602 (2017).
Palyanov, Y. N., Kupriyanov, I. N., Borzdov, Y. M. & Surovtsev, N. V. Germanium: a new catalyst for diamond synthesis and a new optically active impurity in diamond. Sci. Rep. 5, 14789 (2015).
Siyushev, P. et al. Optical and microwave control of germanium-vacancy center spins in diamond. Phys. Rev. B 96, 081201(R) (2017).
Fan, J.-W. et al. Germanium-vacancy color center in diamond as a temperature sensor. ACS Photon. 5, 765–770 (2018).
Bhaskar, M. K. et al. Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide. Phys. Rev. Lett. 118, 223603 (2017).
Iwasaki, T. et al. Tin-vacancy quantum emitters in diamond. Phys. Rev. Lett. 119, 253601 (2017).
Trusheim, M. E. et al. Transform-limited photons from a coherent tin-vacancy spin in diamond. Phys. Rev. Lett. 124, 023602 (2020).
Rugar, A. E., Dory, C., Sun, S. & Vučković, J. Characterization of optical and spin properties of single tin-vacancy centers in diamond nanopillars. Phys. Rev. B 99, 205417 (2019).
Görlitz, J. et al. Spectroscopic investigations of negatively charged tin-vacancy centres in diamond. N. J. Phys. 22, 013048 (2019).
Trusheim, M. E. et al. Lead-related quantum emitters in diamond. Phys. Rev. B 99, 075430 (2019).
DitaliaTchernij, S. et al. Single-photon emitters in lead-implanted single-crystal diamond. ACS Photon. 5, 4864–4871 (2018).
Green, B. L. et al. Electronic structure of the neutral silicon-vacancy center in diamond. Phys. Rev. B 99, 161112 (2019).
Green, B. L. et al. Neutral silicon-vacancy center in diamond: spin polarization and lifetimes. Phys. Rev. Lett. 119, 096402 (2017).
Rose, B. C. et al. Observation of an environmentally insensitive solid-state spin defect in diamond. Science 361, 60–63 (2018).
Thiering, G. & Gali, A. Ab initio magneto-optical spectrum of group-IV vacancy color centers in diamond. Phys. Rev. X 8, 021063 (2018).
Thiering, G. & Gali, A. The (eg ⊗ eu) ⊗ Eg product Jahn–Teller effect in the neutral group-IV vacancy quantum bits in diamond. npj Comput. Mater. 5, 18 (2019).
Harris, I., Ciccarino, C. J., Flick, J., Englund, D. R., Narang, P. et al. Group III quantum defects in diamond are stable spin-1 color centers. Preprint at http://arxiv.org/abs/1907.12548 (2019).
Narang, P., Ciccarino, C. J., Flick, J. & Englund, D. Quantum materials with atomic precision: artificial atoms in solids: ab initio design, control, and integration of single photon emitters in artificial quantum materials. Adv. Funct. Mater. 29, 1904557 (2019).
Bersuker, I. & Polinger, V. Vibronic Interactions in Molecules and Crystals, Springer Series in Chemical Physics Vol. 49 (Springer, Berlin, Heidelberg, 1990).
Qiu, Q.-C. Studies of the doubly degenerate product Jahn-Teller system. Front. Phys. 2, 51–54 (2007).
Qiu, Q. C., Chibotaru, L. F. & Ceulemans, A. Product Jahn-Teller systems: the {T1 ⊗ H} ⊗ (g. 2h) icosahedral exciton. Phys. Rev. B 65, 035104 (2001).
Bersuker, I. B. The Jahn-Teller and pseudo Jahn-Teller effect in materials science. J. Phys. Conf. Ser. 833, 012001 (2017).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Thiering, G. & Gali, A. Ab initio calculation of spin-orbit coupling for an NV center in diamond exhibiting dynamic Jahn-Teller effect. Phys. Rev. 96, 081115 (2017).
Abtew, T. A. et al. Dynamic Jahn-Teller effect in the NV-center in diamond. Phys. Rev. Lett. 107, 146403 (2011).
Ham, F. S. Dynamical Jahn-Teller effect in paramagnetic resonance spectra: orbital reduction factors and partial quenching of spin-orbit interaction. Phys. Rev. 138, A1727–A1740 (1965).
Hepp, C. Electronic Structure of the Silicon Vacancy Color Center in Diamond. Ph.D. thesis (Saarland University, Saarbrucken, 2014).
Viel, A. & Eisfeld, W. Effects of higher order Jahn-Teller coupling on the nuclear dynamics. J. Chem. Phys. 120, 4603–4613 (2004).
Alkauskas, A., Buckley, B. B., Awschalom, D. D. & Van de Walle, C. G. First-principles theory of the luminescence lineshape for the triplet transition in diamond NV centres. N. J. Phys. 16, 073026 (2014).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum: hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 124, 219906 (2006).
Acknowledgements
The authors thank Dr. Tomáš Neuman and Prof. Marko Lončar, at Harvard University, for helpful discussions. This work was supported by the DOE ‘Photonics at Thermodynamic Limits’ Energy Frontier Research Center under grant number DE-SC0019140. D.E. and P.N. are partially supported by the Army Research Office MURI (Ab-Initio Solid-State Quantum Materials) grant number W911NF-18-1-0431 and by the STC Center for Integrated Quantum Materials (CIQM) under NSF grant number DMR-1231319. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Additional calculations were performed using resources from the Department of Defense High Performance Computing Modernization program as well as resources at the Research Computing Group at Harvard University. J.F. acknowledges partial financial support from the Deutsche Forschungsgemeinschaft (DFG) under contract No. FL 997/1-1. The Flatiron Institute is a division of the Simons Foundation. P.N. is a Moore Inventor Fellow through Grant GBMF8048 from the Gordon and Betty Moore Foundation.
Author information
Authors and Affiliations
Contributions
C.J.C. and P.N. conceived the project. C.J.C. and J.F. carried out the calculations and developed the theoretical framework with help from I.B.H. and M.E.T. D.E. and P.N. jointly supervised the work. All authors discussed and contributed to the writing of the manuscript. C.J.C. and J.F. contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ciccarino, C.J., Flick, J., Harris, I.B. et al. Strong spin–orbit quenching via the product Jahn–Teller effect in neutral group IV qubits in diamond. npj Quantum Mater. 5, 75 (2020). https://doi.org/10.1038/s41535-020-00281-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-020-00281-7
- Springer Nature Limited